考虑需求响应和有功损耗的含可再生能源配网节点边际电价

李嫚，李先锋，边俐争，付婷婷

（1.郑州电力高等专科学校，河南郑州 450000；2.华北电力大学电力工程系，河北保定 071003）

0 引言

以可再生能源为代表的分布式电源（Distributed Power，DG）在配网的渗透率逐渐升高，现阶段，DG由被动状态向主动状态转型。因此，适用于输电网络的提高运行效率的方式和机制可以推广到主动配电系统中，例如节点边际电价（Locational Marginal Price，LMP）。配电系统运行商可以根据LMP的状态，对DG机组制定相应的激励措施[1]。

LMP是指某节点增加单位负荷的边际成本，能够反映边际生产成本、边际网损成本和边际输电阻塞成本。LMP机制可以给短期运行和长期规划进行指导。目前对于LMP的研究主要是在输电网领域。文献[2]提出了一种基于LMP的市场过渡期日前出清策略。文献[3]基于LMP对电网风险进行了分析。文献[4]分析了机组运行约束对机组LMP的影响。文献[5]研究了基于LMP的电力市场分区策略。文献[6]针对基于LMP的实时运行阻塞管理展开了研究。文献[7]分析了LMP结算在完全竞争发电市场迭代竞价机制中的作用。文献[8]指出，配网LMP能够有效解决分布式发电接入配网带来的阻塞问题，利用配网LMP，在系统阻塞时，对配网内出力较多、能源需求少的DG机组给予一定激励。目前针对配网LMP的研究还有待深入，通过研究配网LMP，可以有效提升DG在配网的渗透率以及配网的运行优化水平。

目前对于配网LMP模型的求解方法分为分析法、启发式方法、智能人工算法等[9]。启发式算法在求解多参数、非线性问题时应用广泛，主要包括粒子群算法[10]、萤火虫算法[11]、差分进化算法[12]等。但是这些算法大多不能够求解多区域互联的多维度、非凸问题，极易陷入局部最优解。

本文提出了一种考虑需求响应和有功损耗的LMP模型。首先考虑有功损耗的确定性和LMP模型，提出了网损灵敏度因数；针对可再生能源接入配网对节点边际的影响进行了分析和建模，并建立了需求响应模型；建立了以有功损耗最小为目标的LMP模型，并计及约束条件；针对概率场景，采用2m点估计法对模型进行求解；最后在IEEE33节点模型中对算例进行了仿真分析，验证了本文模型的有效性。

1 需求响应和有功损耗模型

1.1 需求响应模型

需求响应项目作为智能电网中的重要组成部分，能够提升电网的运行效率，通过与用户签订相关的协议可以实现对能量使用的转移与削减，从而满足电网运行者的一定需求。需求响应项目通过价格政策和激励政策实现“削峰填谷”，用户收到相应的信号后对其负荷进行相应的调整。总体上来说，根据价格和激励政策的不同，需求响应项目的分类如图1所示[13]。

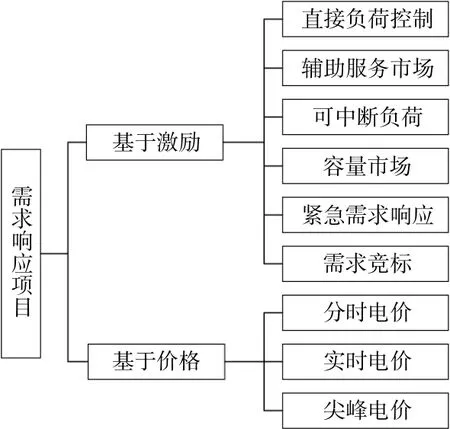
图1 需求响应项目分类Fig.1 Classification of demand response programme

在需求响应的研究中，弹性定义为需求变动与价格变动的比值:

式中:E（t，t），E（t，t′）分别为自需求弹性、交叉需求弹性；PD0（t），PD（t）分别为t时段原始需求、需求响应后需求；τ0（t′），τ（t′）分别为t′时段原始电价、需求响应后电价。

1.2 网络损耗模型

配网的网损不可忽略，因此针对配网的优化一般都以网损最小为目标。

N节点的网络内总的有功和无功损耗可用支路电流的形式计算。

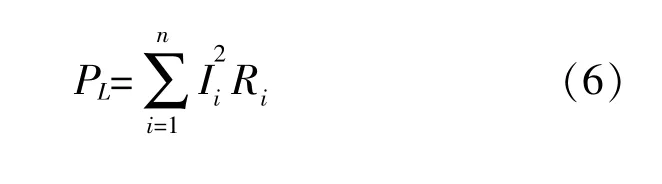
网损灵敏度因数是衡量节点有功和无功对有功网损的影响指标。辐射式配网有功网损对节点i的灵敏度计算式如式（10）所示。类似地，考虑功率因数滞后和超前两种情况，DG机组无功对于节点i的有功网损灵敏度计算式如式（11）和式（12）所示。

式中:IRR，IRI分别为支路电流I与电阻R乘积的实部、虚部构成的矩阵；B为节点支路关联矩阵，其维度与网络内线路和节点数量维度相同。

有功和无功对节点有功网损的贡献计算式分别如下:

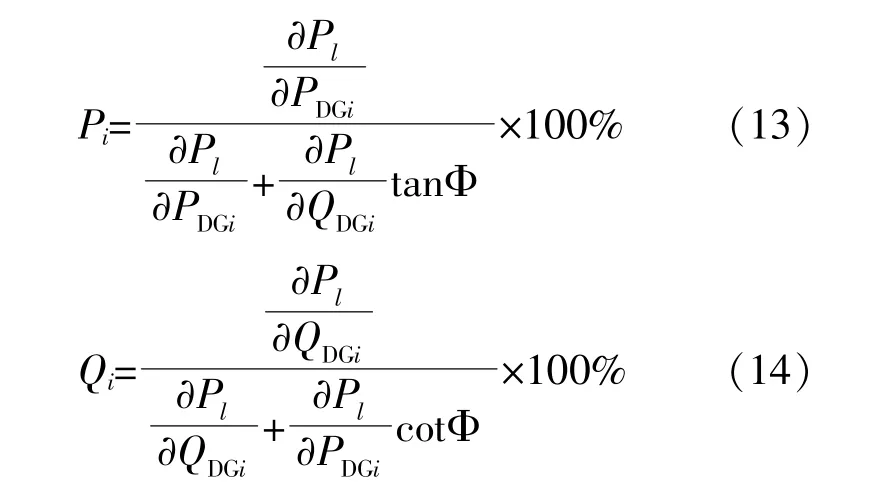
2 配网LMP模型

2.1 含DG的配网LMP模型

配电系统运营商负责配网的调度，利用日前多阶段最优潮流模型进行优化，进而计算配网LMP。假设配电系统运营商运营环境为管制电力市场，即以最大化社会总福利为目标，优化内容包括上级输电系统电价、网络约束、DG发电的成本和约束等。

DG的利润主要与系统总发电成本和总收益有关。

通过求解最优潮流得到LMP。根据不同时段LMP的不同，可以通过需求响应来减少峰谷差和成本。

2.2 约束条件

①功率平衡约束

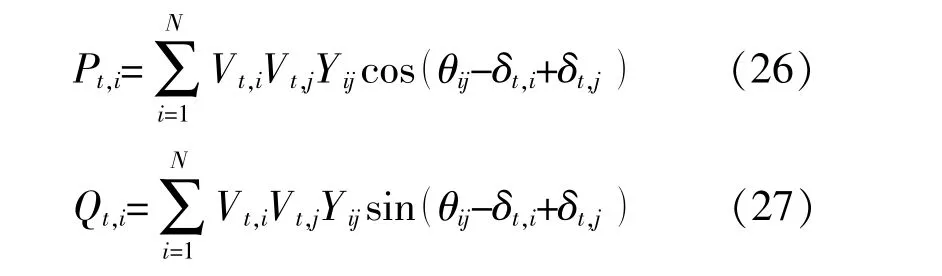
式中:Pt，i，Qt，i分别为节点i在t时段的有功和无功负荷；Vt，i，Vt，j分别为t时段节点i，j的电压，pu；Yij，θij分别为线路ij的导纳和导纳角；δt，i，δt，j为相位；N为节点数。

②机组出力约束

③配电系统运行商净收益约束

配网系统运营商的收益体现在含DG和不含DG的差值中。配电系统运行商的收益计算式如下:

3 配网概率潮流模型求解

3.1 最优潮流求解

配网中的DG可以视为博弈中的参与者。本文利用比例核仁博弈[14]对含有DG损耗问题进行分析。比例核仁理论因其扩展核特性在求解损耗分配问题上具有较高的可靠性。基础情景为不含任何DG注入，在网损分配问题中，DG机组为市场的参与者。考虑该博弈问题为线性规划。

对于本文模型，式（28），（29），（33），（34）统一用h（x，u）≤0表示，x为状态变量，u为控制变量。则拉格朗日函数L表达式如下:

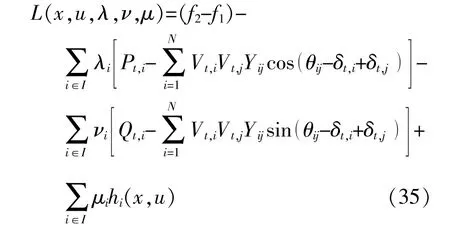
3.2 2m点估计法

不确定性是包括风电和光伏在内的DG出力的性质之一。点估计、缩减泰勒级数和离散算法常用于这类问题的求解[15]。2m点估计法是对原始点估计算法的改进，用于将随机问题分解为若干子问题，在每个不确定变量中选择两个确定值，且这两个值分别位于相应均值两侧。对于每个不确定变量参数，求解两次确定潮流，一次是大于均值的潮流，另一次是小于均值的潮流，而其他均值保持不变。

对于本文模型，有功网损取决于配网中总的负荷需求、DG机组的有功注入以及配网从主网购得的电量。也就是说，配网的网损与负荷以及市场电价等变量有关。从另一个角度说，配网的LMP是具有随机性的，并且与有功负荷以及从主网购电费用有关。

2m点估计法示意图如图2所示。2m点估计法使用每个随机变量的前3个中心元素进行两点分布的估计。

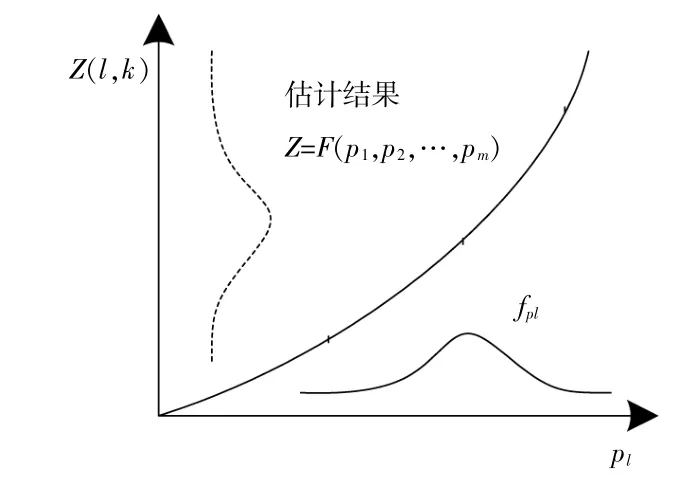
图2 2m点估计法示意图Fig.2 2m point estimation illustration

如图2所示，利用函数关系A=h（x）将输入变量xi，1和xi，2转换为输入变量Ai，1和Ai，2，然后利用权重值pi，1和pi，2对估计值进行赋权，再计算相应的元素值。具体步骤如下:

①确定随机变量数量n；

②设定输出随机变量元素j；

③令i=1；

④计算xi的偏度；

⑤确定集中度的位置；

⑥确定两估计点位置；

⑦求解确定估计点位置；

在上述随机LMP方法中，确定性问题为LMP的迭代问题；

⑧确定权重；

⑨更新输出值；

⑩对所有不确定变量重复步骤③～⑨；确定输出变量的均值和标准差；

11最终得到第j个输出变量的概率密度函数。本文采用2m点估计法步骤如下:

①根据计算的网络模型，明确传统机组和DG机组在各节点的注入值，将该值作为节点注入量的数学期望，根据实际情况确定均值和标准差；

②根据上述模型的数字特征，利用蒙特卡洛方法生成服从指定分布的随机数；

③由这些随机数求得2m点估计法所需的其他数字特征，如偏度等；

④确定需要进行确定性和随机性潮流计算的节点注入量数据，然后利用辐射网前推回代潮流计算方法，得出计算结果；

⑤对计算结果进行统计分析，得到支路功率和节点电压的相关统计数据。

4 算例仿真

4.1 系统说明

本文利用IEEE33节点系统[16]进行仿真，其系统接线图如图3所示。其中:1类机组分布在3，6，23，26，29，19，22节点；2类机组分布在8，11，12，13，31，33节点；3类机组分布在20，27节点。

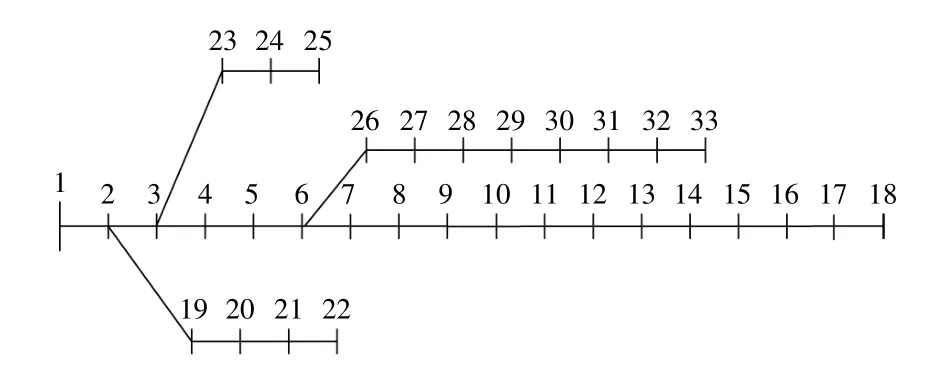
图3 IEEE33节点系统Fig.3 IEEE33 bus feeder

系统负荷和购电费用[17]如图4，5所示，系统需求响应负荷占比为10%和20%。考虑DG容量为1 MW，功率因数为0.9滞后，DG机组的燃料系数如表1所示。

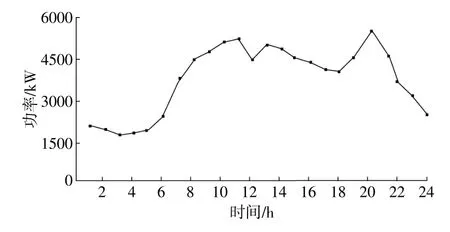
图4 负荷需求曲线Fig.4 Load profile

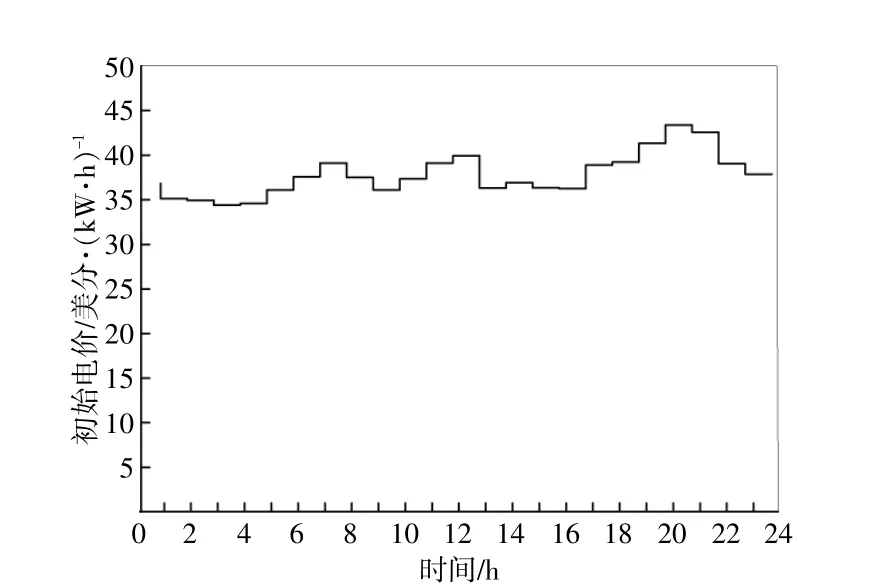
图5 购电电价曲线Fig.5 Electricity price for buyers

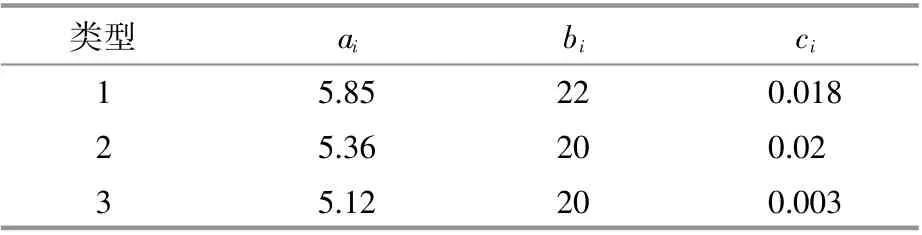
表1 DG机组燃料系数Table 1 DG location and size

4.2 算例分析

在算例分析中，本文考虑电价确定情景和概率情景两种情景。

（1）确定情景

以各DG机组为研究对象，考察其在某一调度时段各参数的变化情况。图6给出了确定性算法中每台DG机组的LMP，当购电价格为21.09，26.19$/（MW·h）时，DG机组可以根据LMP的激励参与有功网损削减。在不同的市场电价下，各DG机组有不同的LMP。由于DG11相比其他机组对有功网损削减的贡献更多，因此其LMP更高。配电系统运行商可以根据本文方法对DG机组提供一定的LMP激励以优化市场竞争。

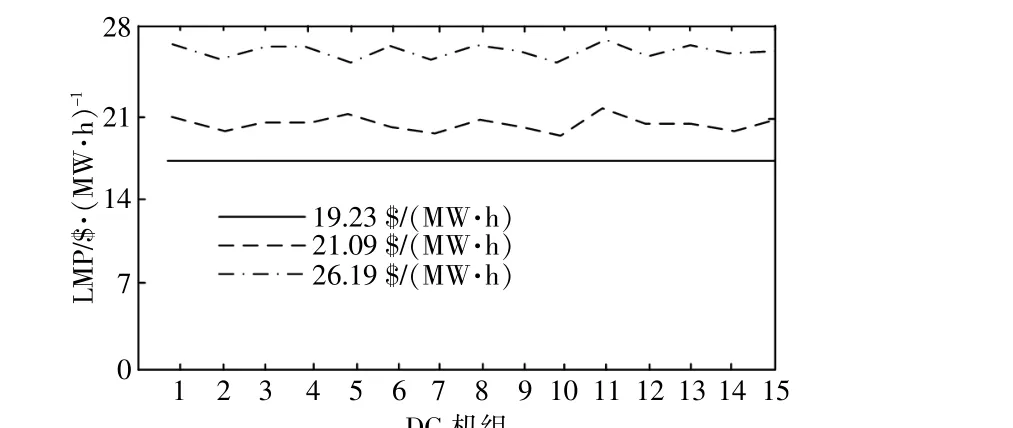
图6 确定情景LM PFig.6 LMP of determined scenario

图7给出了不同市场电价下各DG机组有功出力，当市场电价为21.09，26.19$/（MW·h）时，DG机组有功出力与配电系统运行商的LMP激励有关。在给定LMP下，DG机组的有功出力值会使DG机组所有者的收益最大。DG11机组仍然在有功出力削减中贡献最大，所以受到最大激励，该机组的有功注入最大。

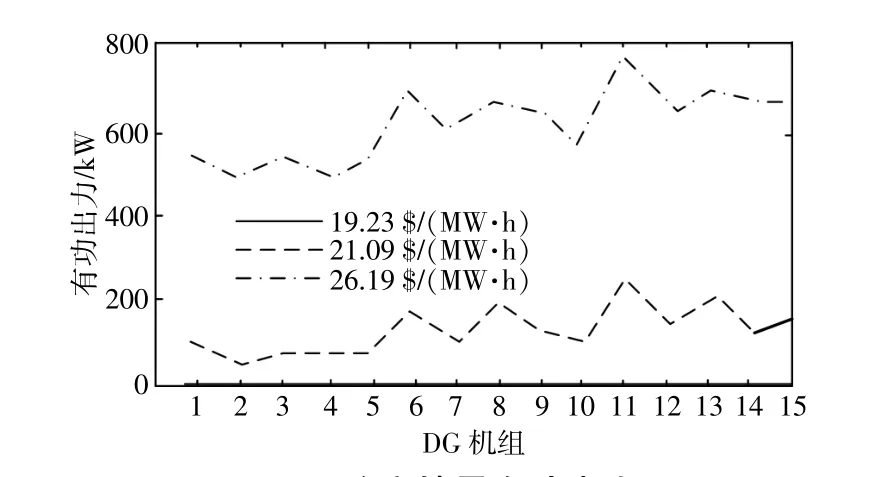
图7 确定情景有功出力Fig.7 Active power output in determined scenario

图8给出了不同市场电价下各DG机组的无功电价。市场电价下各DG机组的无功电价取决于与有功网损削减相对应的无功注入。同理，DG11机组的无功电价更高。

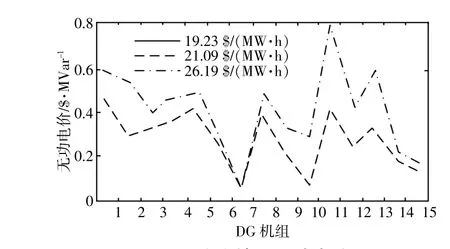
图8 确定情景无功电价Fig.8 Reave power output in determined scenario

如图8所示，当市场电价为19.23$/（MW·h）时，因DG机组的状态均未得到有效激励，此时所有机组的发电成本系数b均高于市场电价。同理，图7中DG机组出力为0，图8中针对无功出力也没有激励。

图9给出了配电系统运行商在不同市场电价的收益。确定情景有功网损如图10所示。配电系统运行商的额外收益为DG机组注入下产生的网损削减相比不含DG机组情景的经济收益，该收益与主网购电和电力用户的用电费用、DG机组运维差额无关。根据DG机组在网损削减中的贡献程度进行激励可以优化市场竞争，配电系统运行商可以从额外收益中给予DG机组用户一定的激励，充分提高配电系统运行商的额外收益。

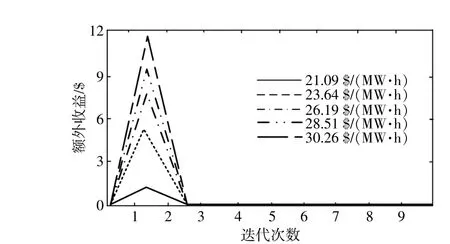
图9 配电系统运行商额外收益Fig.9 Extra profit of distributor

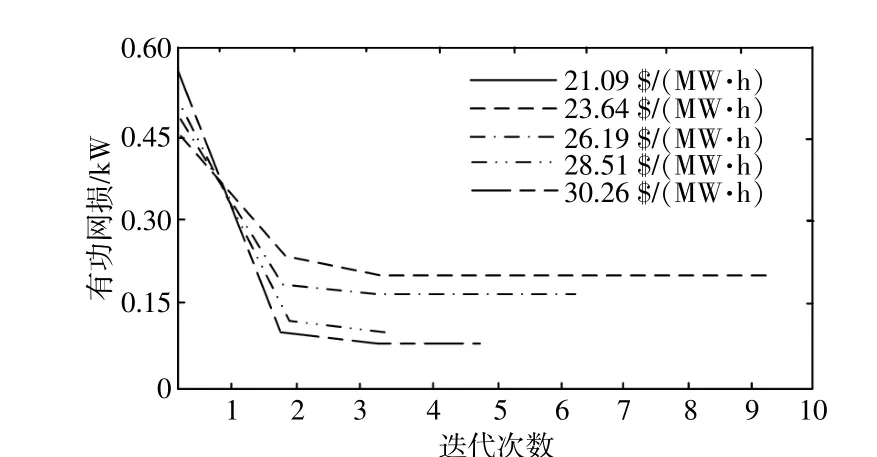
图10 确定情景有功网损Fig.10 Active power losses of determined scenario

针对需求响应对网损的影响，以DG10机组为研究对象，在市场电价为26.19$/（MW·h）时对整个调度周期进行考察，设定负荷占比α=10%和20%两种情况进行对比，结果如图11所示。

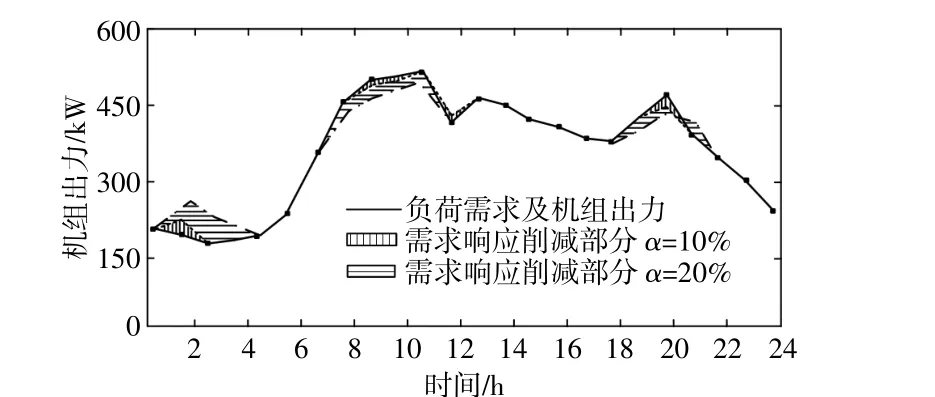
图11 需求响应下机组出力Fig.11 Power output under demand response

由图11可以看出，随着需求响应参与度的提高，DG机组在整个调度周期内的出力曲线更加平滑，反映为峰荷时段出力下降，低谷时段出力上升，能够起到一定的负荷转移作用。但是在不同的电价下情况会有所差异，本文以较高的市场电价为研究对象，其LMP也较高，对于用户的激励作用较为明显。

（2）概率情景

本文考虑负荷以及市场电价的概率特性进行仿真。图12给出了基于DG机组对有功网损削减的贡献而得到的LMP。在市场电价为21.09，26.19 $/（MW·h）时，DG机组受到LMP激励。DG11机组对LMP的影响更大，因此受到的激励也越大。

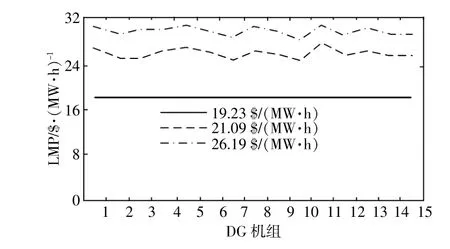
图12 概率情景LMPFig.12 Probabilistic LMP of determined scenario

图13给出了DG机组的概率有功出力。在一定的市场价格下，有功出力取决于DG机组的LMP。DG11机组的出力最大，这也是由于其受到LMP的激励最大。

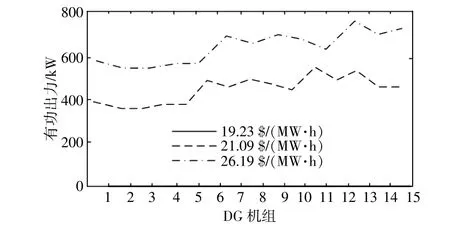
图13 概率情景有功出力Fig.13 Active power output in probabilistic scenario

图14给出了DG机组的概率无功电价，该值与DG机组对有功网损削减程度有关。DG11机组的网损削减最大，因而无功电价也最大。

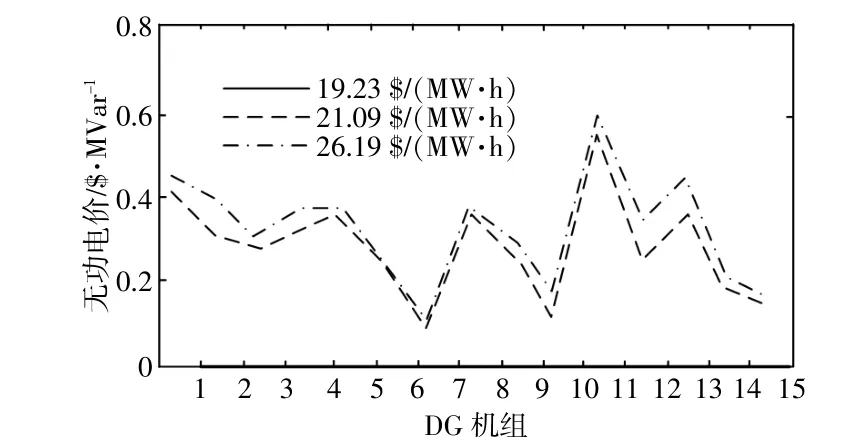
图14 概率情景无功电价Fig.14 Active power output in probabilistic scenario

如果市场价格为19.23$/（MW·h），并小于所有机组的收益值，机组就会因为缺少激励而停止发电，这与确定情景的情况相同。针对概率情景，表2给出了有功网损削减方面的对比。可以看出，概率情景下能够捕捉到DG机组周边的不确定信息（负荷和电价变动），这与确定情景有所差别。在基础情景下，配网不含DG机组，此时存在变动的负荷，如果仍然采用2m点估计法计算网损，则网损对于随机性的灵敏度不高。

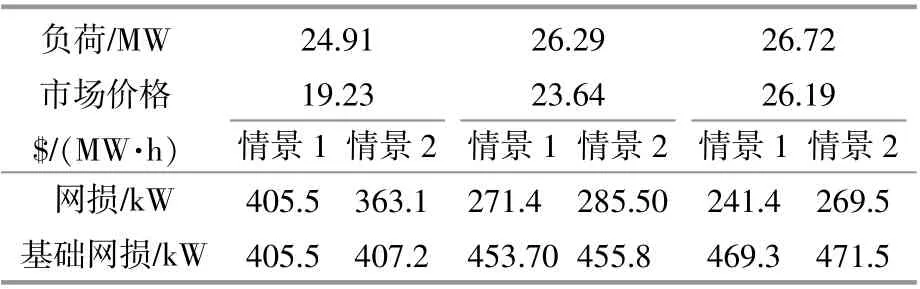
表2 情景对比Table 2 Comparison of different scenarios

（3）2m点估计法与其他算法对比

为了验证2m点估计法在本文问题求解中的有效性，选择有功网损作为考察对象，对比结果如表3所示。

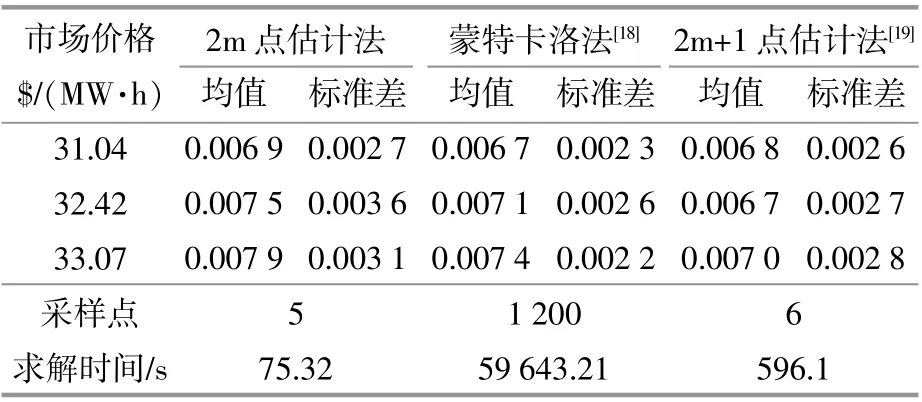
表3 有功网损对比Table 3 Comparison of active power loss

由于蒙特卡洛法模拟的样本量大，精度更高，因此可以作为参照，但是该方法耗时较大，不适用于快速分析，并且受样本值的影响较大。由表3可以看出:在求解时间上，2m点估计法的优势最大；2m点估计法与2m+1点估计法相差不大，在考虑求解精度和求解效率方面，2m点估计法用于求解实时变化的配网潮流更为合适。

5 结论

①在概率情景下，市场电价对DG机组出力、需求响应负荷有很大影响，低于一定阈值时，DG机组收益为负而不选择出力。

②在高市场电价时，DG机组收益较多，向电网注入功率，使得节点边际电价升高，同时考虑确定情景下节点边际电价的波动要小。因此在配网最优潮流计算中，应当将负荷和市场电价的波动考虑其中。