弱电网下LCLLC滤波的并网逆变器电流优化控制策略

徐永，王海云，王维庆

（新疆大学可再生能源发电与并网技术教育部工程研究中心，新疆乌鲁木齐 830047）

0 引言

并网逆变器控制性能会影响可再生能源发电系统的稳定运行[1]，但随着可再生能源在电网中所占的比例越来越高，以及远距离输电和变压装置损耗，为了不影响并网逆变器的控制性能，不能忽略电力系统中电网的等效阻抗[2]，[3]。

目前，国内外学者在并网逆变器控制策略方面做了大量研究[4]。文献[5]提出了一种滤波性能更好的LCLLC滤波器，它不仅具有LCL滤波器的滤波性能，还可以对特定频次的谐波进行抑制，但没有对其进行相应控制策略的分析。文献[6]提出了一种LCL滤波器下的准比例积分谐振（PIR）控制策略，它将比例积分（PI）和准比例谐振（QPR）控制器结合起来，有效提高了并网电流的跟踪能力和电能质量，但没有分析弱电网下对控制系统性能的影响。针对弱电网下控制系统的稳定性，文献[7]采用了一种电网电压全前馈的控制策略，该控制策略理论上可以完全消除弱电网对逆变系统所带来的影响，但校正环节的微分项实现起来较为困难，并且会放大噪声。文献[8]提出了一种电网电压比例前馈控制策略，它可以抑制电网电压中低次背景谐波对控制系统性能的影响，但随着电网阻抗的增大，系统的相位裕度逐渐减小，系统稳定性下降。

本文以LCLLC滤波器为基础，提出了PIR控制的双闭环电流控制策略。另外针对弱电网下的等效电网阻抗对并网逆变器控制性能的影响，建立了诺顿等效电路，分析了电网阻抗变化对控制系统稳定性的影响。提出了一种加入权重系数后的电网电压比例前馈控制策略，该控制策略可以减小电网阻抗对控制系统产生的影响，提高并网逆变器在弱电网下的稳定性。

1 LCLLC滤波的并网逆变器模型

在电力系统中，通常强电网的短路比（SCR）为20～25，弱电网的SCR为6～10。当并网点（PCC）呈现出弱电网特性时，电网阻抗也会随着逆变器并网点位置的变化而改变。图1为三相并网逆变器主电路拓扑结构图。

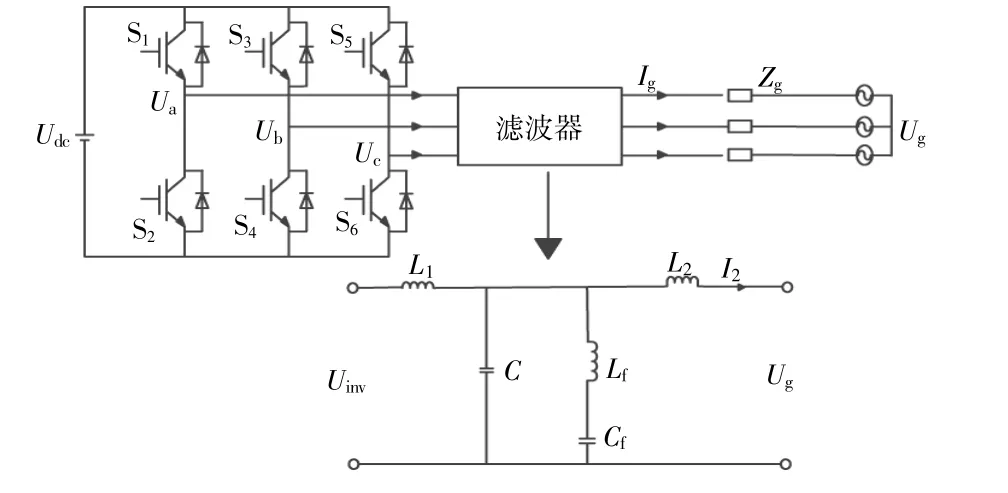
图1 三相并网逆变器主电路拓扑结构图Fig.1 Topology diagram of main circuit of three-phase grid-connected inverter

图中:Ug，Ig，Ii分别为并网电压、并网电流和滤波器逆变侧的输入电流；本文以直流源UDC代替光伏发电部分；Uinv，I2，L1，L2，Lf，Cf，C分别为滤波器的逆变侧电压、并网电流、逆变侧电感、网侧电感、串联谐振支路的电感、串联谐振支路的电容、滤波电容；Zg为电网等效阻抗。由于电阻不影响系统稳定性，故只考虑电网电感的影响[9]，即Zg=Lg。

由图1可知，LCLLC滤波器在LCL滤波器基础上，并联了一个LC串联谐振电路，将LC串联谐振支路的谐振频率设置为开关频率时，可对逆变侧输出电流中开关频率fsw周围的谐波表现为零阻抗，从而降低整个并网电流谐波含有量[10]。

由图1可得逆变器传递函数为

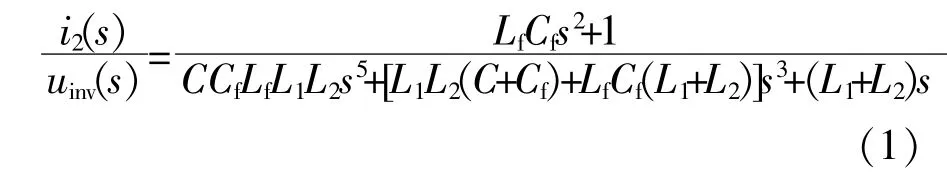
图2为3种不同形式滤波器的Bode图。

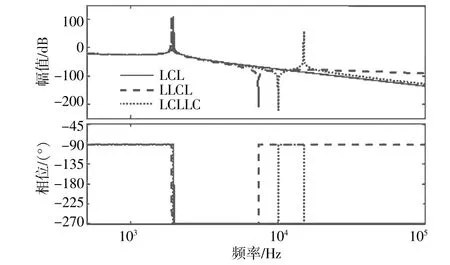
图2 3种不同形式滤波器的Bode图Fig.2 Bode diagram of three different types of filters

由图2可知，LLCL型滤波器在串联谐振频率处形成了一个负谐振峰，能消除特定频率的高次谐波，并且在低频段它的衰减特性与LCL型滤波器基本一致，但在高频段的衰减特性要明显弱于LCL型滤波器[11]。LCLLC型滤波器既能消除特定频次的谐波，还兼顾了LCL滤波器每10倍频程-60 dB的高频衰减特性[12]。

2 并网逆变器的控制策略

2.1 PI和QPR控制器原理

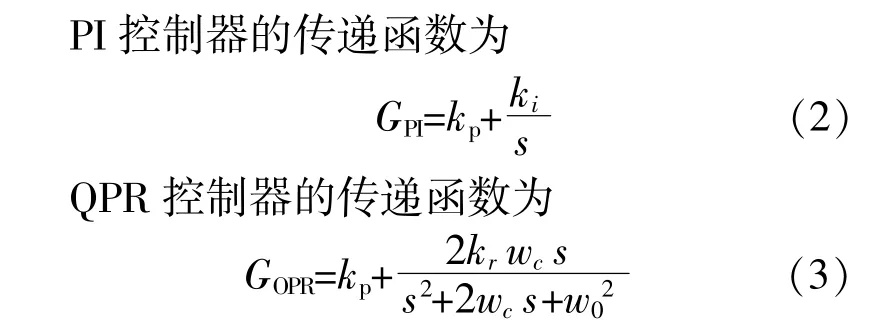
PI控制器在基波频率处的增益较小，而在低频直流附近具有较大的增益，因此它可以对直流分量进行无静差跟踪[13]。而QPR控制器在基波频率处具有较大增益和带宽，它可以对交流分量进行无静差跟踪[14]。为了提高逆变系统的电流跟踪效果和并网电流的质量，根据两种控制器不同的跟踪特点，将两种控制器并联形成准比例积分谐振（PIR）控制器[15]，它可以对逆变侧的交直流分量分别控制，抑制电流谐波分量，则PIR控制器传递函数为[16]

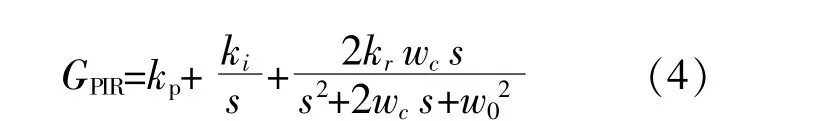
式中:kp为比例系数；ki为积分系数；w0为基波的角频率；wc为谐振控制器带宽；kr为基波频率处的增益。

2.2 弱电网下传统电网电压前馈系统稳定性分析

系统控制结构框图如图3所示。

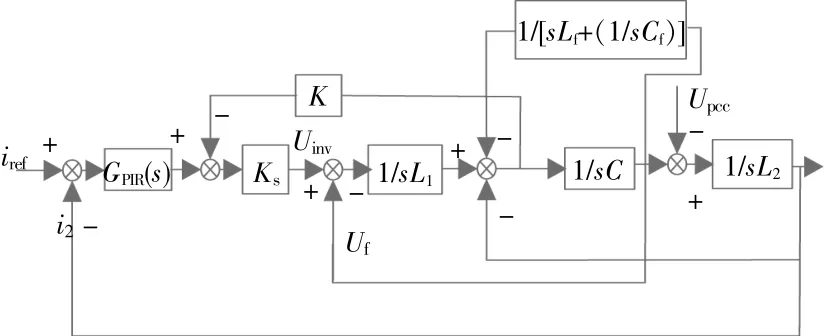
图3 系统控制结构框图Fig.3 System control structure block diagram

并网逆变器控制策略是将滤波电容电流反馈量经过比例反馈后作为电流内环，而外环是将并网电流反馈量与给定电流参考值的差值输入到PIR控制器中进行电流跟踪控制，从而实现对整个并网逆变系统的控制。图中:GPIR（s）为PIR控制器传递函数；Ks为脉宽调制系数，采用空间矢量脉宽（SVPWM）调制技术；K为电容电流反馈系数；iref为给定的并网电流参考值；i2为并网电流；Upcc为并网点电压。

将系统控制结构框图简化后如图4所示。

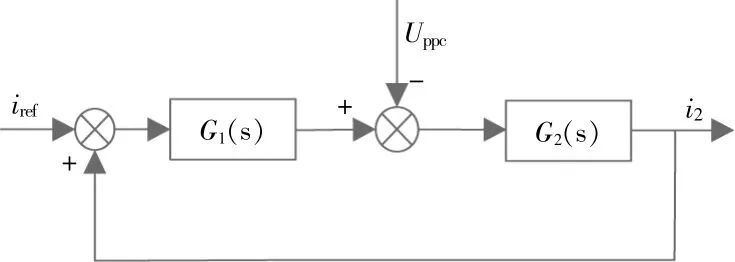
图4 系统等效控制框图Fig.4 System equivalent control block diagram

图中:G1（s）=GPIRKs（Lfs2+1）/A；G2（s）=A/B；A=L1LfCfCs4+KsKLfCfCs3+（L1C+LfCf+LfCf）s2+KsKCs+1；B=CCfLfL1L2s5+KKsL2LfCfCs4+[L1L2（C+Cf）+LfCf（L1+L2）]·s3+KKsCL2s2+（L1+L2）s。

根据简化后的系统控制框图可以得到并网电流的表达式为

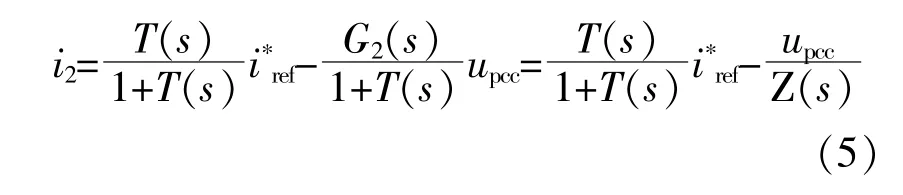
式中:Z（s）为逆变器输出阻抗；T（s）为系统的开环增益，T（s）=G1（s）G2（s）。

由式（5）可以看出，输出的并网电流由两个变量控制，一是给定的参考电流控制；二是并网点电压控制。该部分由于电网电压的扰动以及电网阻抗的存在会对并网电流产生影响，故应采取一定的措施抑制对并网电流的影响[17]。

在电网中除了基波外还有一些低次背景谐波，这会增加并网电流的畸变率，所以为了减小背景谐波的影响，常采用直接电网电压比例前馈控制，其比例系数的表达式为

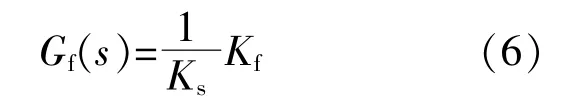
式中:Kf为权重系数，当Kf=1时，表示传统的直接电网电压比例前馈。

在弱电网下，电网阻抗会对系统稳定性造成影响，引入电网阻抗Zg后，系统控制框图如图5所示。

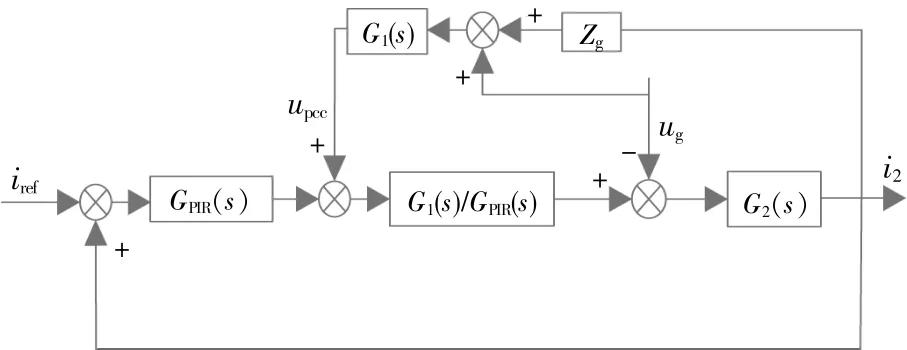
图5 比例前馈控制下的系统控制框图Fig.5 Control block diagram of the system under proportional feedforward control

电网阻抗中等效电网电阻对系统稳定性基本没有影响，而等效电网电感是造成系统稳定性下降的主要原因。因此，本文考虑最恶劣即纯电感条件下，系统的开环传递函数为

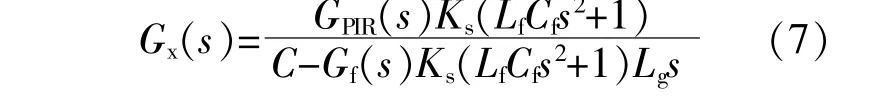
式中:C=CCfLfL1Lds5+KKsLdLfCfCs4+[L1Ld（C+Cf）+LfCf（L1+Ld）]s3+KKsCLds2+（L1+Ld）s；Ld=L2+Lg。

图6分别为在采用传统的直接电网电压比例前馈（Kf=1）时，系统在强电网和弱电网下的传递函数Bode图。

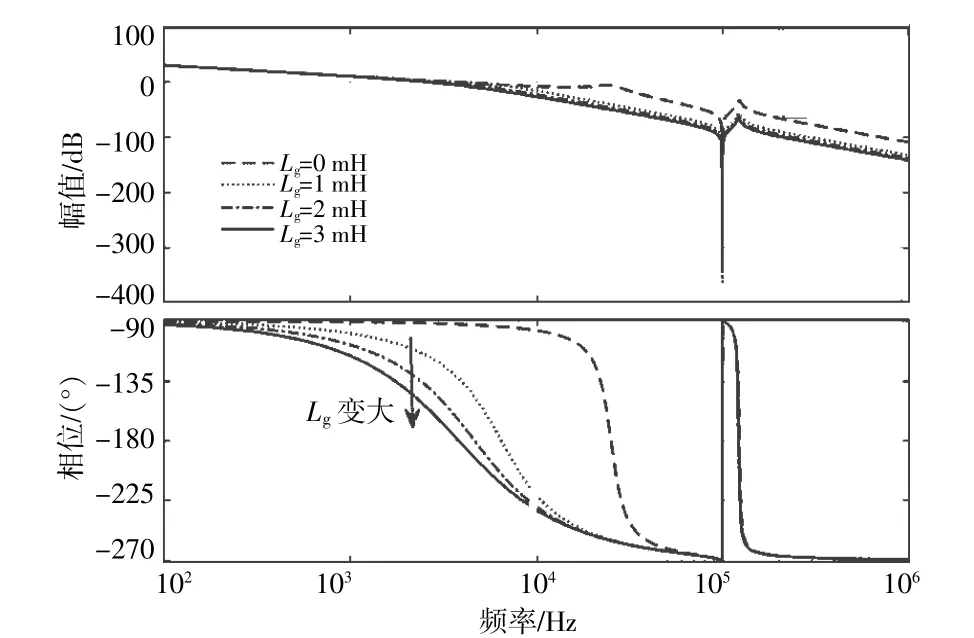
图6 不同电网阻抗下系统传递函数Bode图Fig.6 Byrd diagram of system transfer function under different network impedances

由图6可以看出:在强电网Lg=0 mH时，逆变器相位裕度接近90°，逆变器能够稳定并网运行；在弱电网下，Lg从0～3 mH的过程中，系统的相位裕度急剧下降，说明随着电网阻抗的不断增大，并网逆变器的稳定裕度也会不断变小，造成并网逆变器的稳定性下降。

2.3 弱电网下改进后的电网电压前馈系统稳定性分析

将并网逆变器等效为诺顿等效电路，即将逆变器等效为受控电流源并联逆变器输出阻抗，而电网则为理想电压源Ug与电网等效阻抗Zg（s）串联，电路如图7所示。

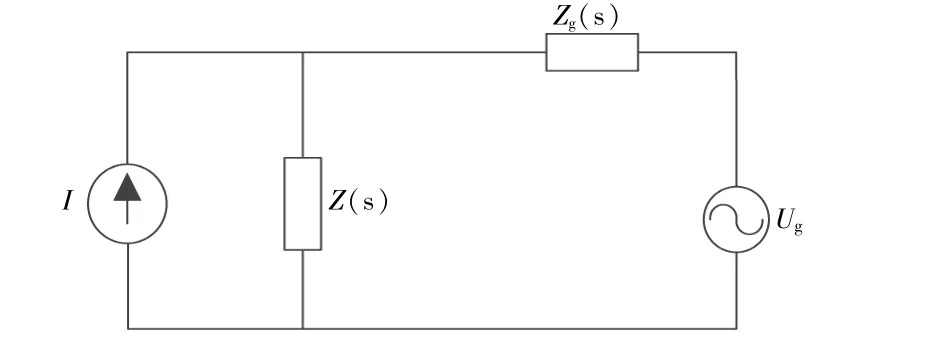
图7 诺顿等效电路Fig.7 Norton equivalent circuit

根据系统阻抗稳定性判据，逆变系统在电网阻抗的影响下，保持稳定须满足两个条件:①逆变器自身在并入强电网时能够稳定运行；②逆变器的输出阻抗和电网阻抗的比值Z（s）/Zg（s）满足奈奎斯特稳定判据。即满足Z（s）和Zg（s）幅频曲线的交点（频率ωs）处的相位裕度大于0°。相位裕度表达式为

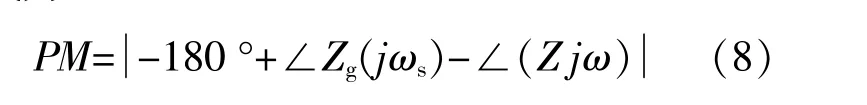
假设电网阻抗以纯电感表示，得到新的相位裕度表达式为

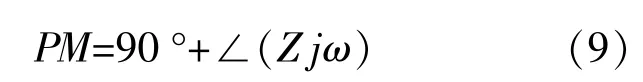
由式（9）可以看出，要使相位裕度大于0，则逆变器等效输出阻抗相频曲线的相位就要大于-90°。本文对电网电压比例系数中加入相应的权重系数Kf，以改善系统的稳定性。

根据图5，采用改进的电网电压比例前馈后，并网逆变器的输出阻抗表达式为

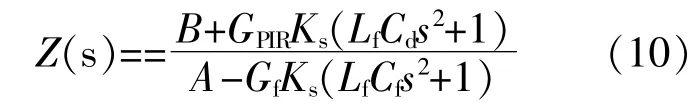
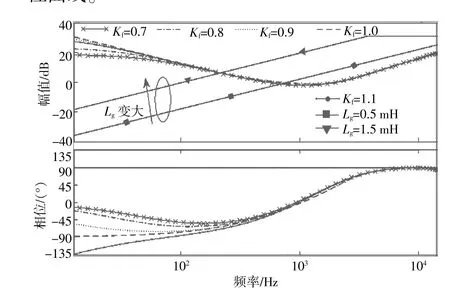
图8 逆变器输出阻抗与电网阻抗的幅频特性曲线Fig.8 Amplitude-frequency characteristic curve of inverter output impedance and network impedance

逆变器采用传统的电网电压比例前馈（Kf=1）时，逆变器的输出阻抗相位基本维持在-90°以上，但在一些低频段接近-90°。说明电网阻抗增大，当逆变器输出阻抗与电网阻抗的幅频曲线交点逐渐左移到该频段时，系统虽能稳定，但稳定裕度很低，极易发生失稳现象。因此，本文将比例前馈系数乘以适当的权重，来提高稳定裕度，当Kf增大时（Kf=1.1，1.2），随着逆变器输出阻抗与电网阻抗的幅频曲线交点逐渐左移，逆变器输出阻抗的相频曲线低于-90°，由式（11）可知，此时的相位裕度小于0°，即系统不稳定。当Kf减小时（Kf=0.9，0.8，0.7），在相同的电网阻抗下，相位裕度有所增大，并且在一定范围内，电网阻抗增大，逆变器输出阻抗与电网阻抗的幅频曲线交点逐渐左移，系统稳定性有所减小，但基本都保持在-90°以上。

由图9可以看出，加入权重系数以后，随着电网阻抗Lg从0 mH增大到3 mH时，系统传递函数的幅频曲线中的截止频率减小，但它的相频曲线中的相位裕度并未受较大影响，始终保持在80°左右，仍满足系统稳定性的要求。

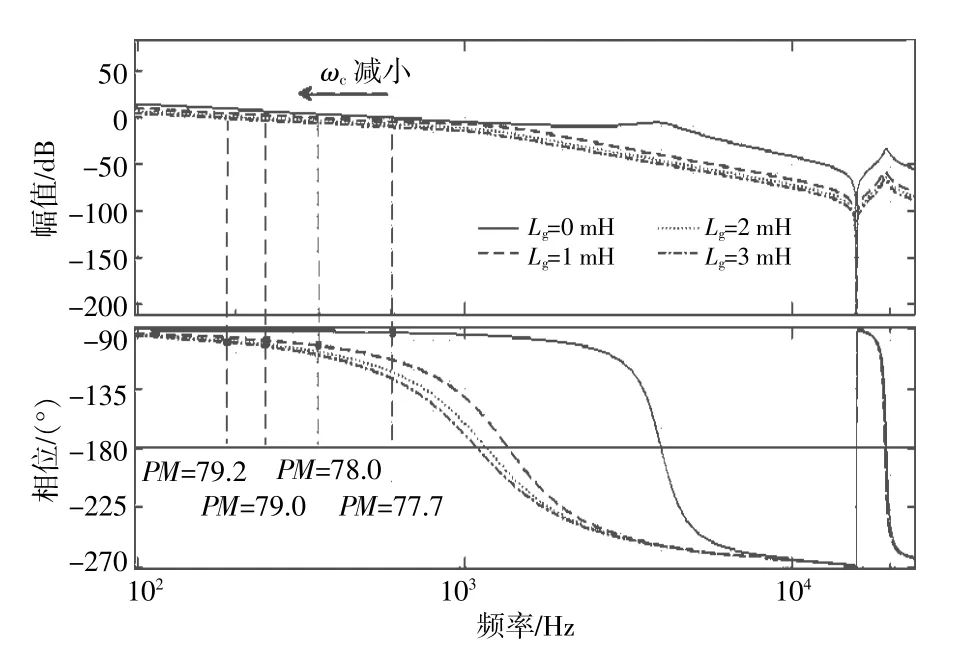
图9 K f=0.8时系统传递函数Bode图Fig.9 Bode diagram of system transfer function when K f=0.8

3 仿真分析

为了证明本文所提方法的可行性，利用Matlab/Simulink软件搭建了三相逆变系统的仿真模型，其系统仿真参数如表1所示。

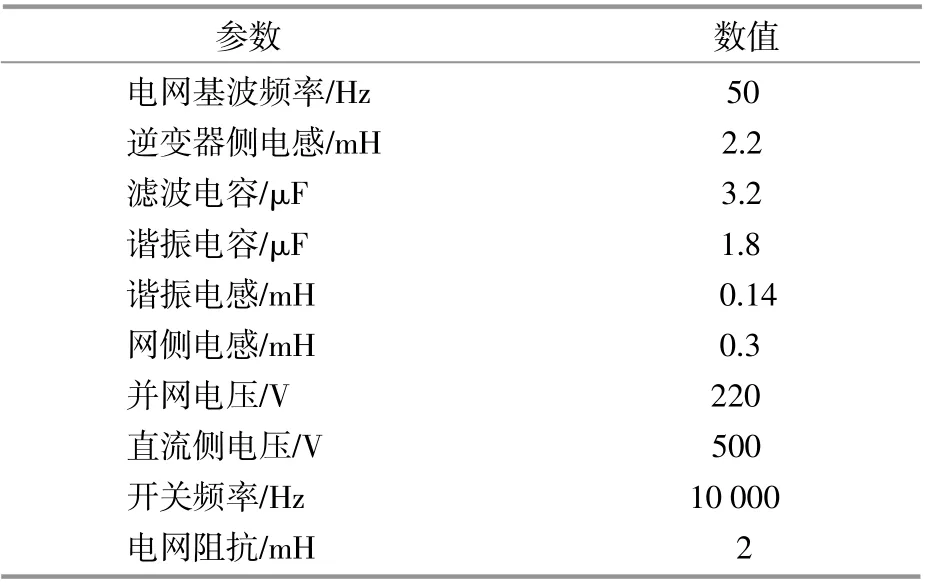
表1 系统仿真参数Table 1 System simulation parameters table

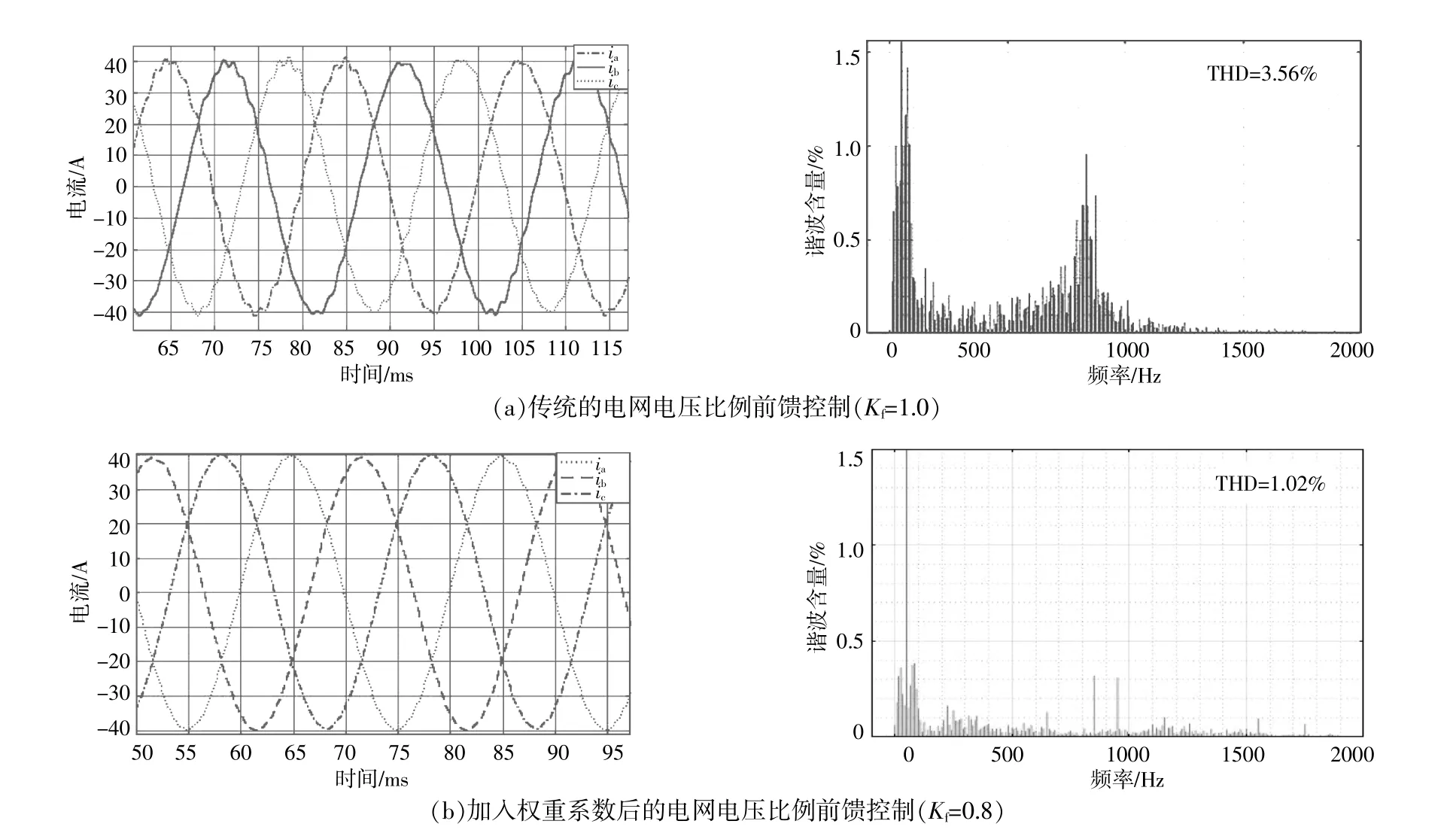
图10 输出的并网电流波形和谐波含量分析图Fig.10 Grid-connected current waveform output and harmonic content analysis diagram

由图11可以看出，并网电流和电网电压达到了同频、同相位的并网要求，并且在参考电流指令突变的情况下，并网电流也能够稳定跟踪参考电流指令的变化。说明逆变系统所采取的控制策略能够稳定实现入网电流的突变并且具有快速的动态响应能力，实现了对并网电流信号的无静差跟踪。

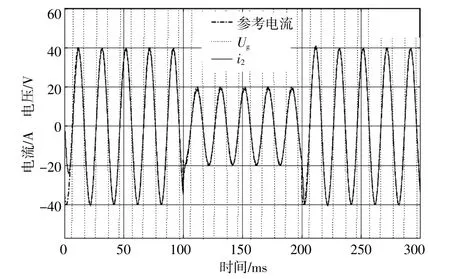
图11 单相并网电流电压波形图Fig.11 Waveforms of single-phase grid-connected current and voltage

4 结论

本文以光伏并网系统所用的并网逆变器为研究背景，利用LCLLC滤波器提出一种在弱电网下的并网逆变器电流控制策略。文中所采用的PIR电流跟踪控制器可以有效地改善电流跟踪效果和系统动态响应能力。另外，对于弱电网下的电网阻抗造成系统稳定性下降的问题，本文提出了加入权重系数的电网电压比例前馈控制策略，提高了系统的相位裕度，减小了低频谐振，使并网电流具有更好的电能质量。