整车主动悬架平顺性时域仿真与优化

荣吉利， 邓增琨， 何丽， 王玺， 程修妍

(1.北京理工大学 宇航学院，北京 100081；2.北京航天发射技术研究所，北京 100076；)

平顺性是体现出车辆整体性能水平的重要参数之一，车辆的操纵稳定性、制动性、动力性以及通过性与平顺性有一定的关联[1]. 某大型特种运输车是目前常用的地面运载装备[2]，此种运输车将面临恶劣的路面条件以及高强度的操作要求，对平顺性要求较高. 传统车辆采用被动悬架的设计，对路面的适应能力低，难以兼顾平顺性与操纵稳定性的要求. 相对于被动悬架，主动悬架理论上可以更好地满足车辆的平顺性要求，提高车辆的综合性能. 因此主动控制的研究对车辆综合性能提高有重要意义.

郑育龙[1]建立基于仪器-车-路耦合的19自由度振动动力学模型，结合粒子群算法，对相关参数进行了优化分析. 赵子男[3]建立了1/2车的路面激励下振动模型，采用层次分析法讨论了LQG控制方法中性能指标加权参数的选择方法. 张志超[4]建立了整车7自由度模型，设计了主动悬架LM-BP神经网络控制器和改进粒子群神经网络间接自适应控制器. RAME等[5]基于线性最优控制理论，对1/4轿车悬架系统进行了优化设计与分析，并比较SQP和GA算法得到最优参数. 李鑫军等[6]建立了考虑座椅振动的8自由度整车动力学模型，基于最优控制理论，设计了以主动悬架性能指标为目标函数的LQG控制器.

文中将某大型特种运输车简化为17自由度的路面-车耦合模型，基于现代控制理论建立多输入多输出的动力学状态方程，通过LQG控制理论设计车辆主动悬架控制器，并利用粒子群算法对LQG控制器的加权参数进行优化，得到主动悬架的最优控制规律，提升车辆平顺性与整车综合性能水平.

1 建立仿真模型

1.1 路面不平度模拟

路面不平度是车辆产生振动的主要原因[7]，利用线性滤波白噪声法，可模拟车轮接触的路面条件. 车辆左轮路面激励的数学模型微分方程为

(1)

式中:q(t)为路面对车轮的激励；v为车速；nc=0.01 m-1为截止空间频率；n0=0.1 m-1为标准空间频率；W(t)为均值为0的平稳白噪声.

左右轮在空间域中具有一定的相关性，根据左右轮相关性的状态方程和输出方程[8]可得车辆右轮的路面激励.

(2)

(3)

式中:W1和W2分别为左右轮的白噪声输入；x1和x2为状态变量；a0=3.181 5；a1=0.206 3；a2=0.010 8；b0=3.223；b1=0.590 0；b2=0.032 7.

1.2 车辆模型简化

简化整车为17自由度模型如图1所示. 将车身、轮胎、支架以及仪器作刚体假设，只考虑车辆在同等级别路面的匀速直线运动和路面垂直方向的激励，忽略车辆横向以及纵向的激励[9].

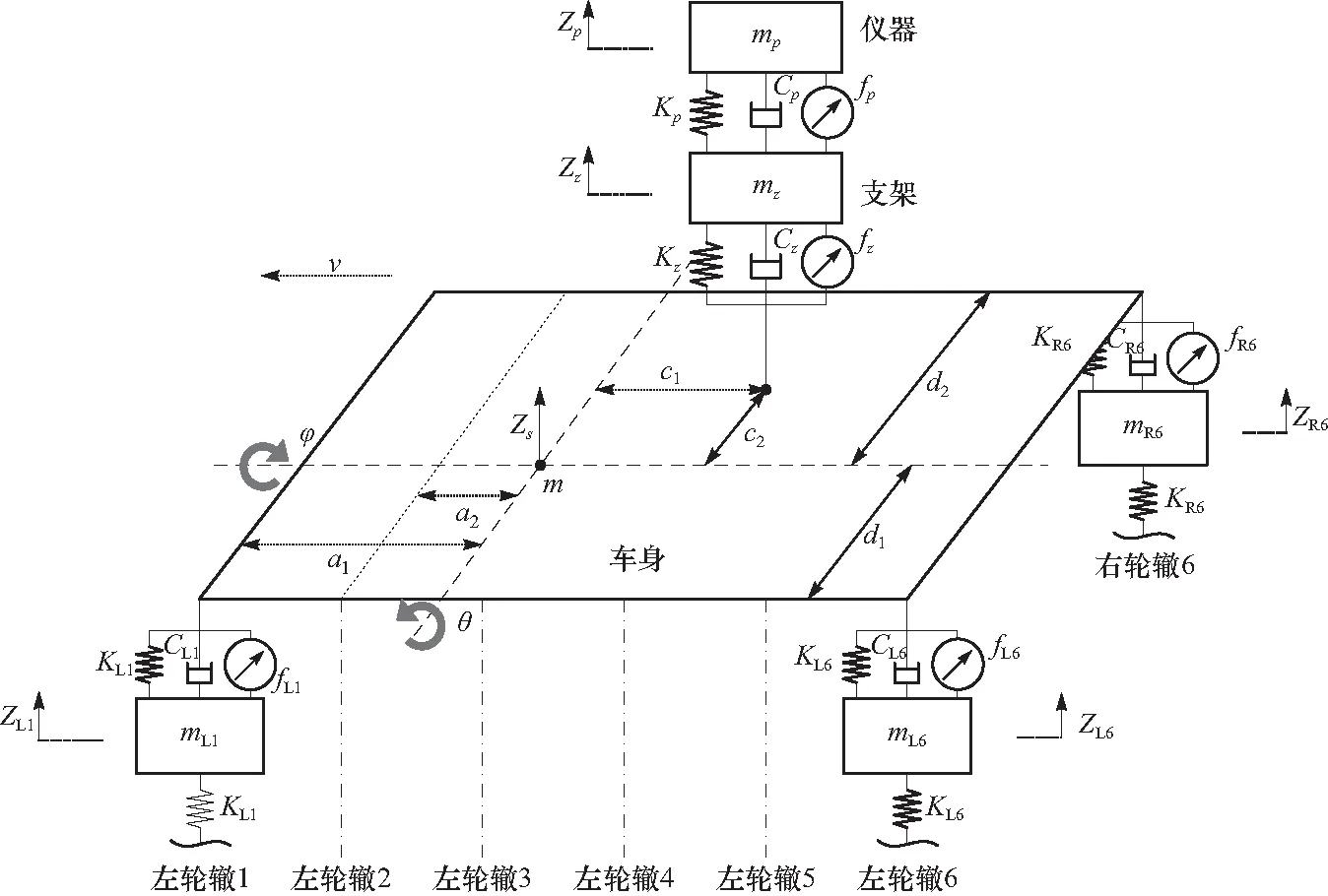
图1 17自由度整车简化模型

1.3 建立路面-车耦合振动力学模型

根据非保守系统下的广义Lagrange方程：

(4)

式中:qi为系统的广义坐标；Ek为系统动能；Ep为系统的势能；Dp为系统的耗散能；Qi为系统外部所受广义力(或为力矩).

根据式(4)即可建立17自由度的路面-车耦合的振动微分方程，其矩阵形式为

(5)

其中，整车系统的17个广义坐标为

Z=[ZL1ZL2…ZL6ZR1ZR2…ZR6ZsθφZzZp]T

2 LQG控制

2.1 系统状态方程

对于整车17自由度模型来说，需要考虑到如下性能指标：仪器垂向加速度与车身垂向、俯仰角、侧倾角加速度，仪器、仪器支架以及悬架和轮胎的动位移.

可选择系统状态变量：

根据整车性能指标的要求，设置状态方程的输出向量为

Y=[Y1Y2]T

其中：

Y2=[ZL1-qL1…ZL6-qL6ZR1-qR1…

ZR6-qR6Zz-Zs-c1θ+c2φZp-Zz]

其中，yL1…yL6,yR1…yR6为车辆悬架在12个轮胎处的动位移.

控制器的控制向量为U：

U=[fL1…fL6fR1…fR6fzfp]T

根据式(1)至式(3)的轮胎路面激励模型，可得到系统的扰动向量W：

W=[wL1…wL6wR1…wR6]T

式中，wLi,wRi(i=1,2,…,6)分别为左右车轮的随机白噪声输入.

结合式(5)可得到系统的状态方程

(6)

2.2 线性二次型高斯控制器的设计

车辆主动悬架设计的要点在于根据系统的振动特性选择最优的控制规律，对应的主要工作为：寻找最优控制规律，使系统在稳定工作的前提下，其性能参数得到优化[10]. 对于本文所设计的主动悬架系统，其主要目的是提升车辆行驶的平顺性，并相应地改善车辆综合性能.

因此可得线性二次型控制最优控制性能指标泛函J.

qRi)2+q7(Zz-Zs-c1θ+c2φ)2+q8(Zp-Zz)2+

(7)

式中:q1,q2,q3为车身垂直、俯仰角与侧倾角加速度的加权系数；q4仪器垂向加速度的加权系数；q5为各轮胎处悬架动位移的加权系数；q6为轮胎动位移的加权系数；q7和q8分别为仪器支架动位移和仪器动位移的加权系数；r1,r2,r3分别为轮胎、仪器支架和仪器处作动力的加权系数.

将式(6)代入到式(7)可得：

(8)

则可得最优控制规律：

U=-KX

其中，K为最优反馈增益矩阵：

K=R-1BTP

式中，矩阵P可由Ricatti方程得出：

PA+ATP-PBR-1BTP+Q=0

(9)

在Matlab中，矩阵K可直接用LQR函数[11]求得：

[KPe]=LQR(A,B,Q,R,N)

式中:P即为Ricatti方程的解；e为系统特征值.

因此可得到闭环系统的状方程：

(10)

3 粒子群优化

LQG控制器的加权参数会影响车辆综合性能的表现，可通过粒子群优化算法[12-15]对整车性能指标泛函进行优化，得到相应的最优加权参数. 设置目标函数F为

(11)

式中:α1,α2,α3为主动悬架车身垂直加速度、俯仰角加速度、侧倾角加速度均方根值；α4为主动悬架仪器垂向加速度均方根值；α5～α16分别为主动悬架12个轮胎处车辆悬架的动位移均方根值；α17～α28分别为主动悬架12个轮胎处动位移的均方根值；α29与α30分别为主动悬架仪器支架动位移与仪器动位移的均方根值；βi(i=1,2,…,30)分别为被动悬架对应的均方根值；pi(i=1,2,…,30)分别为各性能参数均方根比值的加权，可根据设计要求进行调节.

经过反复调整和试验设计，充分考虑到每一个性能指标重要程度，可设置：

p1=20,p2=p3=2,p4=100,

pi=3(i=5,6,…,16),

pi=1(i=17,18,…,28),p29=4,p30=10

根据式(7)，整车LQG控制器粒子群优化的变量为

q=[q1q2…q8r1r2r3]T

经过反复调整，修改优化变量的取值范围，最终得到整车LQG 控制器优化的数学模型可描述为

min(F)

(12)

利用Matlab进行粒子群优化算法的编程，设置粒子群规模为20，总共进行100次迭代，可得优化后的各加权参数为

q1=222,q2=150,q3=575.3,q4=881.3,

q5=239.6,q6=10-4,q7=227.4,q8=124.6,

r1=3.28×10-6,r2=1.348,r3=0.045

根据此加权参数，通过式(9)可得到车辆悬架系统主动控制最优控制规律K. 根据式(10)，在SIMULINK中得到主动悬架和被动悬架性能参数的仿真结果，将被动悬架和主动悬架各性能参数进行对比，其中体现车辆行驶平顺性的仪器加速度和车身垂向加速度对比如下：

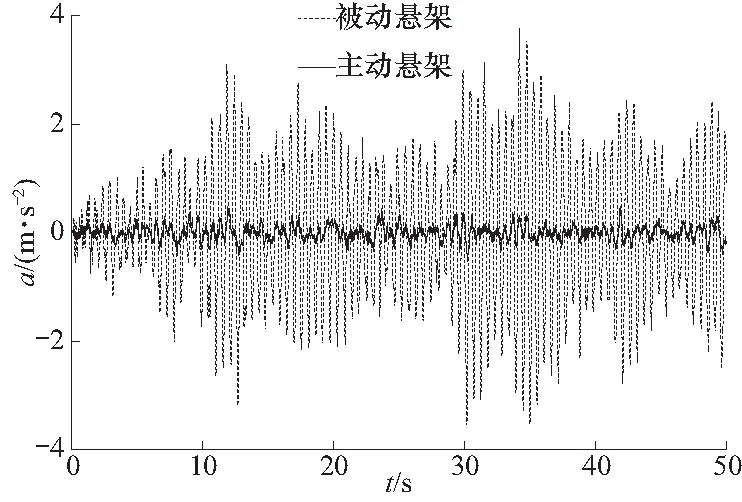
图2 仪器加速度

图3 车身垂向加速度

被动悬架和主动悬架整体性能参数对比如下：

图4 被动悬架和主动悬架性能参数对比

通过改变车速与路面状况，可得到优化的控制规律在不同环境下对车载仪器的平顺性的优化效果.

通过表1与图5、6可得，主动悬架在不同路面激励、不同车速的情况下，仪器的振动加速度有着良好的优化效果，车辆行驶平顺性相对于被动悬架都有较大的提升. 其中图5中车速60 km/h的情况下，被动悬架车辆共振效果明显，而主动悬架可以相应地减轻共振带来的影响. 通过对比主被动悬架形式车辆的仪器振动加速度，得到采用该主动悬架设计的车辆的鲁棒性较高，车辆可适应不同路面与不同速度的变化情况.

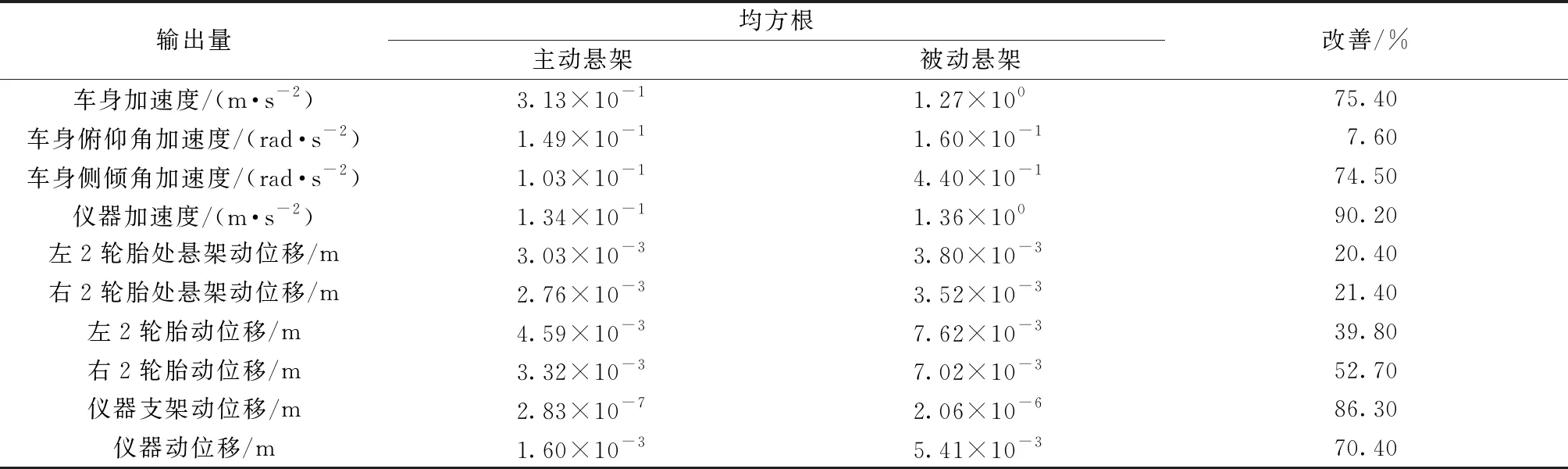
表1 主动悬架和被动悬架各性能参数的均方根值

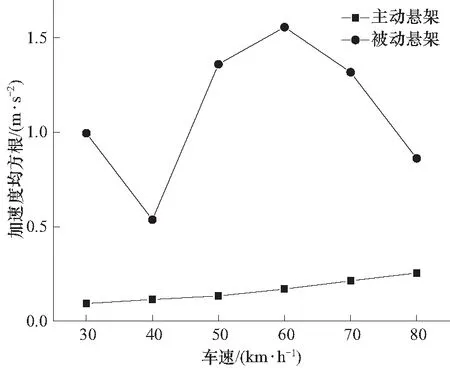
图5 C级路面激励下不同车速仪器振动加速度均方根

图6 50 km/h下不同级别路面激励的仪器振动加速度均方根

4 结 论

针对车辆在行驶过程中，因剧烈振动造成的平顺性与稳定性降低的问题，建立了路面-车耦合的17自由度动力学方程，利用LQG理论对车辆进行主动悬架控制器的设计，通过粒子群算法对LQG控制的加权参数进行优化，得到了最优的控制规律. 仿真结果表明，此LQG控制方法可以改善车辆行驶的平顺性，同时车辆的操纵稳定性、结构稳定性均有所改进，而且此控制规律下的主动悬架有较好的鲁棒性.