干片式制动器支撑结构的拓扑优化方法

任毅如， 向剑辉， 杨玲玲， 宁克焱

(1. 湖南大学 机械与运载工程学院，湖南,长沙 410082；2. 中国北方车辆研究所，北京 100072)

随着技术的不断发展，车辆在动力和速度等方面的性能不断提升，为了保证车辆行进过程中的灵活机动性和安全可靠性，需要对制动器性能提出更高的要求.

车辆制动器主流的形式有鼓式和盘式两种，其中盘式制动器又分为钳盘式和全盘式，全盘式制动器也被称为片式制动器. 制动器根据摩擦条件分类可以分为干式和湿式. 为了揭示并改进制动器结构性能，大量学者对车辆制动系统展开多方面的研究[1-5]，制动器的结构优化设计方面的研究就是其中重点. 张义民等[6]采用随机摄动技术和Hooke-Jeeves直接搜索优化方法对钳式盘形制动器以相关尺寸参数为设计变量进行了多目标可靠性优化设计. SONG等[7]针对热弹性失稳问题利用Kriging代理模型对周向摩擦的盘式制动器进行了减重优化设计. PARK等[8]对圆盘式磁流变制动器进行了优化设计. 曲杰等[9]采用一种基于代理模型的复杂结构优化设计方法对通风盘式制动器的动盘结构作了优化设计，在以寿命最大化为目标的设计中取得了较好的结果. 余健等[10]采用变密度的拓扑优化方法基于Optistruct对盘式制动器制动钳体进行了模态分析优化，使钳体质量更小的情况下模态频率得到降低.

干片式制动器由于其制动性能优、结构简单可靠以及适用性广等特点[11]，被广泛应用于军用履带式车等重型车辆中. 尽管关于片式制动器的研究很多，大都针对温升规律等方面的研究. 同时，关于制动器轻量化的研究同样重要，而关于制动器轻量化的研究目前还处于起步阶段[12]. 由于干片式制动器在制动器服役过程中，制动器支撑结构变形过大导致制动器易出现卡滞等问题，在轻量化的同时需要控制变形的大小，目前亟需却鲜有对该问题的研究. 拓扑优化设计可以改变材料分布和拓扑构型，极大扩大结构设计域[13-18]. 变密度拓扑优化方法由于计算效率高，算法易于实现并且应用相对方便，得到了广泛的应用[19]. 为了改善干片式制动器结构性能，针对支撑结构卡滞问题，建立了制动器支撑结构控制变形的拓扑优化设计模型，并对某型履带车辆制动器结构进行了优化设计.

1 干片式制动器支撑结构

1.1 干片式制动器结构

干片式制动器主要由加压机构、摩擦片组以及支撑结构组成，如图1所示为某种典型的干片式制动器结构简图，图中壳体为制动器支撑结构. 加压机构主要由转动盘、移动盘及其作用的弹子组成，并且通过滚珠与支撑结构作用在一起. 摩擦片组包括静摩擦片和动摩擦片，动摩擦片通过内圈的齿轮跟随转动轴转动，静摩擦片通过外圈的凸缘作用于支撑结构上，在与动摩擦片摩擦时保持相对静止，如图2所示.

图1 某典型干片式制动器结构示意图

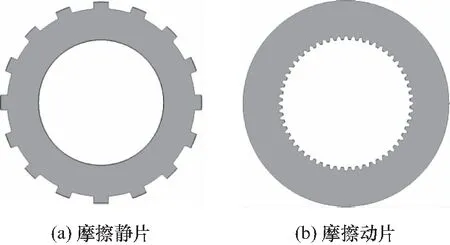
图2 摩擦片结构示意图

1.2 制动器支撑结构

如图3所示为一个典型的干片式制动器支撑结构，支撑结构留有周向分布的等距间隙，允许摩擦静片产生轴向移动和限制其周向转动. 在支撑结构的支撑支柱上开有孔洞结构，起到了减重和散热的作用. 该支撑结构作为优化设计的初始结构.

在制动过程中，加压机构将作用于转动盘上的周向操纵力转化成轴向的压紧力，以此来压紧摩擦片组. 摩擦动片和摩擦静片相互的摩擦作用产生制动力，而制动力最终通过静片的凸缘作用在制动器支撑结构的支柱上，如图3中载荷1所示. 在产生压紧力时，压紧力的反作用力通过加压机构与支撑结构之间的滚珠对支撑结构产生一个轴向的拉伸作用力，大小等于压紧力，如图3中的载荷2所示. 此外，在转动盘转动过程中，转动盘与支撑结构内壁间会产生摩擦力. 由于摩擦力相对较小，忽略该摩擦力，仅考虑载荷1和载荷2的作用. 这两个载荷将作为支撑结构拓扑优化设计的载荷条件.

图3 支撑结构及其载荷位置示意图

根据制动器结构及工况特点，支撑结构空隙间会有摩擦静片的作用，上方有和转动盘配合工作的作用，均不适于作为设计区域. 支撑结构支柱中的孔洞设计是用来减轻结构重量的，因此将其填满后可作为设计区域，支撑结构模型如图4所示.

图4 支撑结构模型

2 支撑结构拓扑优化方法

2.1 变形最小目标下支撑结构拓扑优化设计方法流程

拓扑优化设计方法，就是在给定的边界约束条件和载荷下，寻求材料在优化区域内满足特定目标的最优分布.变密度的拓扑优化方法由于其简单高效的特点得到了广泛的应用.

拓扑优化依赖于有限元方法，变密度拓扑优化方法的设计变量为每个单元的弹性模量，为了便于计算，将弹性模量换算为0～1连续取值的伪密度[20]. 变密度法的核心思想就是对每一个单元的伪密度进行更新迭代，并且借助惩罚函数对其进行惩罚使其更加趋于0，1分布，然后用伪密度0来表示单元的去除，用伪密度1来表示单元的保留. 变形最小目标下的拓扑优化选取关键节点的位移作为优化目标，结构体积大小作为约束条件. 在优化过程中，对优化迭代是否终止的判断，对设计变量的更新均依赖于有限元分析的结果. 在进行拓扑优化设计时，有限元分析、设计变量的更新等均需要遵循特定的流程，按照流程可以有序地完成各项分析计算工作. 具体的设计流程如图5所示.

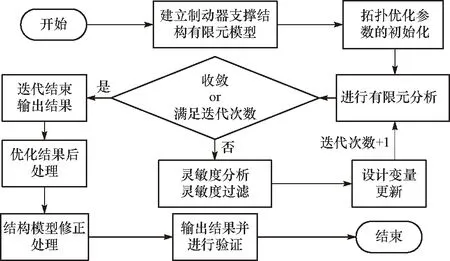
图5 制动器支撑结构拓扑优化设计流程

2.2 变形最小目标的拓扑优化设计方法理论基础

变密度法可以根据需要选用不同的插值模型，其中最为常用的是固体各向同性材料惩罚模型(solid isotropic material with penalization，SIMP)，采用了SIMP模型的变密度方法又叫SIMP法[20]. 变密度法拓扑优化方法的数学模型为

(1)

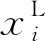
拓扑优化设计可以根据实际情况选择适当的目标函数，其中使用最多的目标函数之一是柔度，用结构柔度最小来表示刚度最大. 采用SIMP法的柔度目标函数可以表示为

(2)

式中：U为结构的整体位移矩阵；K为结构的整体刚度矩阵；ui和ki为单元i的单元位移矢量和单元刚度矩阵；p为惩罚因子，对SIMP方法来说，一般取值为3. 则目标函数的灵敏度为

(3)

对于干片式制动器，在制动过程中若支撑结构产生较大变形可能会导致支撑结构与转动盘之间的配合间隙过大，环境中的杂物就会进入间隙对制动器的性能及寿命产生严重影响，甚至直接失效无法工作. 因此，将制动器支撑结构与转动盘配合位置的变形作为优化设计目标是必要的. 对于考虑变形问题的结构，通常以关键节点与相对应的目标位置之间的距离最小作为目标函数，则变形目标函数为

(4)

(5)

(6)

(7)

或者

(8)

3 干片式制动器支撑结构的拓扑优化设计

3.1 建立拓扑优化有限元模型

在对干片式制动器支撑结构进行拓扑优化设计前，需要对模型做一定的简化，去除掉不在设计范围内的小结构，如螺纹孔，倒角圆角等，这样可以优化有限元网格的质量. 对需要设计的孔洞区域需要进行填充，提供可用的设计区域. 如图6所示为支撑结构简化后建立的有限元模型，总共包含44 208个单元. 支撑结构材料在常温下弹性模量为211 GPa，泊松比为0.3，抗拉强度为930 MPa，屈服应力为735 MPa.

图6 支撑结构简化有限元模型

3.2 边界条件、约束条件及目标函数的设置

根据前文分析，对支撑结构的边界条件进行了简化，将支撑结构支柱的底面固定，将15 kN的周向力和60 kN的拉伸力施加在支撑结构上，分别施加在如图3中的载荷1和载荷2所示位置.

为了不破坏非必要的区域，将这些区域冻结，不参与拓扑优化设计，作为非设计区域，其他区域为设计区域. 为了对比不同设计区域下的拓扑优化结构，设置了3种不同的设计区域，如图7中(a)、(b)和(c)所示. 图7(a)所示扩展支柱结构设计域冻结了支撑结构与加压机构接触配合的部分，支撑立柱及其上方的结构均为设计区域；图7(b)所示支柱无约束设计域仅仅将支撑支柱作为设计区域，其他区域冻结；图7(c)所示支柱边界固定设计域在图7(b)设计域的基础上对支柱结构的周向的边界和底面进行了限制，不作为设计区域，仅对支柱结构径向及内部区域进行优化，这样可以保持支柱外形在周向的完整性. 考虑到设计区域相对于整个结构较小，故将拓扑优化设计的体积约束设置为待优化模型即图6所示模型结构的60%，该设置后简称体积约束.

图7 3种不同的设计域示意图

干片式支撑结构为循环对称结构，但由于优化问题不具备严格凸性以及数值化整误差的问题，循环对称载荷边界条件下的循环对称结构优化出来的结果不一定具有循环对称的特点[21]. 循环对称约束条件可以将结构强制约束成循环对称，故对支撑结构添加了循环对称约束限制.

针对支撑结构在巨大的载荷下产生过大的变形而导致的卡滞问题，选择支撑结构上缘配合面的上下两条边的关键节点的最大位移最小为设计目标. 考虑到计算量的问题，在上下两条边处各选取了25个点作为关键点，即将设计目标设为50个点的最大位移最小，以此来表示结构的变形最小. 如图8中实心圆点所示.

图8 50个目标关键点示意图

3.3 拓扑优化设计结果及分析

3种不同设计设计区域下的制动器支撑结构拓扑优化结果如下图所示. 图中3种情况下的优化结果具有较大的区别，其中图9(a)和图9(b)中的优化结果没有保留完整的加载面，由于摩擦静片在压紧过程中会发生轴向的移动，故会对制动器的功能造成一定的影响. 图9(c)结构支柱之间的空隙保留完好，设计相对保守，可作为进一步设计的参考.

图9 3种不同设计域下拓扑优化结果

为了获得相对可靠的设计参考，在支柱边界固定设计域情形下，增加将体积约束设置为70%和80.14%(初始结构设计方案体积)的情形进行结构拓扑优化设计，得到的结果如图10(a)、(b)所示，在支撑支柱的右下角处均为类三角形的通孔，外表面居中位置形成了一个类似于梯形的较大的浅槽，和类三角形通孔叠加在一起. 图10(b)支柱的孔和槽相对图10(a)更小.

图10 支柱边界固定设计域下70%和80.14%体积约束拓扑优化结果

对初始结构设计下的制动器支撑结构进行有限元分析，其等效应力分布云图和位移分布云图分别如图11中(a)、(b)所示. 在载荷施加的位置以及结构较薄弱的位置应力较大，包括支撑支柱两侧载荷施加位置、上方凸缘位置以及支撑支柱内侧直角处位置等，最大应力为48.67 MPa，小于支撑结构材料许用应力值. 节点位移则是在距离固定端越远的位置位移越大，变形最大处为支撑结构距离固定端最远的上方凸缘处，该处节点位移为2.123×10-2mm. 这个位置与加压机构之间存在主要的配合作用，变形过大将严重影响制动器的性能.

图11 初始设计方案仿真分析结果

支柱边界固定设计域情形下3种不同体积约束下拓扑优化的结果的等效应力分布云图和位移分布云图如图12所示. 其中(a)(b)分别为60%体积约束下优化结果的等效应力云图和位移云图，(c)(d)分别为70%体积约束下优化结果的等效应力云图和位移云图，(e)(f)分别为80.14%体积约束下优化结果的等效应力云图和位移云图. 3种情形下支撑结构的最大应力分别为38.52 MPa、17.70 MPa以及16.67 MPa，小于许用应力值且较初始结构设计有所改善. 在60%体积约束下，由于去除了过多的材料的缘故，其最大节点位移较初始方案大，70%体积约束和80.14%体积约束下最大节点位移都较初始方案小，证明了优化方法的有效性.

图12 支柱边界固定设计域情形下不同体积约束优化结果的对比

在70%体积约束时，优化结果变形最大位置的节点位移为2.098×10-2mm；80.14%体积约束时，即优化体积与初始方案一致时(实际体积与约束体积会存在一定的误差)，最大节点位移为1.918×10-2mm. 两种情况下的优化结果最大节点位移均优于初始方案，变形相对更小.

对于上述通过拓扑优化直接得到的结果，由于包含一定数量的中间密度单元，其结构不能作为最后的优化结构. 故需要根据优化结果的结构特征，对该干片式制动器支撑结构进行模型修正重建.

根据拓扑优化结果中类三角形通孔和类似梯形的较大梯形浅槽的结构特点，在支撑结构支柱的左下角设置了一个直角三角形的通孔，然后在支柱外表面设置了一个类似梯形的浅槽，最后对棱角位置设置合适大小的圆角，得到了最后的优化模型. 结构特征尺寸通过测量得到，结合拓扑优化结果的中间密度单元分布，通过对测量得到的三角形通孔尺寸、浅槽的尺寸和深浅进行合适的增减以及对不同位置圆角的大小进行调整，得到4个体积不同的优化结果，分别为减重15%设计方案，其体积为324 567 7 mm3,相对初始方案减少15.7%，最大节点位移增加4.7%，在体积减少较多的情况下，最大变形相对初始方案有所增加；减重10%设计方案，其体积为345 801 0 mm3，相对初始方案减少10.2%，最大节点位移和初始方案相当；变形优化减重方案，其体积为361 869 8.25 mm3，相对初始方案减少6.0%，最大节点位移减少4.1%；等体积设计方案，其体积为385 165 9.5 mm3，非常接近初始方案，最大节点位移减少9.4%. 4个优化模型的应力分析结果均优于初始结构，其有限元模型及应力分布云图和位移分布云图为图13所示，相对于初始方案在相关参数上的对比如表1所示.

图13 4种优化模型的有限元分析结果

表1优化模型仿真结果

4 结 论

拓扑优化设计方法通过改变结构的设计区域，约束限制条件等优化参数获得不同的拓扑优化结果. 在60%体积约束和扩展支柱结构、支柱无约束和支柱边界固定3种不同设计域情况下，扩展支柱结构和支柱无约束优化结果支柱结构表现为一个上粗下细的斜柱结构，扩展支柱结构设计域结果相对支柱无约束优化结果去除了支柱上方结构的材料，而支柱本身更粗壮；支柱边界固定设计域的结果则形成了类似桁架的结构.

在支柱边界固定设计域而体积约束分别为60%、70%和80.14%的情况下，70%体积约束和80.14%体积约束下拓扑优化的结果类似，不同于60%约束结果的类桁架结构，其支柱上左下角有一个类似于三角形的通孔，并且在外表面形成了较大的沟壑，区别在于80.14%体积约束下的通孔和沟壑的尺寸更大.

最后的4个优化模型孔洞由较小的类三角通孔和较大的浅槽组成，得到了一种不同于初始结构的设计方案. 减重10%设计方案在保证目标性能相当的情况下体积减少了10.2%；等体积设计方案在体积相当的情况下，最大节点位移减少了9.4%；变形优化减重方案在体积减少6.0%的情况下，最大节点位移减少了4.1%.