显式有限元侵蚀接触搜索算法研究

陈成军， 陈小伟， 柳明

(1.中国工程物理研究院 总体工程研究所，四川,绵阳 621900；2.北京理工大学 前沿交叉科学研究院，北京 100081；3.北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

高效、健壮、精确的侵蚀接触算法是弹体穿甲/侵彻、高速碰撞等冲击动力学问题数值模拟的关键，是拉格朗日显式有限元方法研究与发展中的重要课题之一. 所谓“侵蚀接触”是指在接触-碰撞过程中，由于材料损伤破坏而删除相应单元导致新物质界面产生，新界面继而与附近物质发生接触作用. 与一般的动态接触问题相比，侵蚀接触计算存在很大挑战：接触点与接触片随时间动态变化，原有接触点/接触片可能随单元删除而消失，伴随产生新的接触点/接触片，接触对在空间和时间上很难预测；接触界面不平滑，接触片不规则，点-面、边-面、边-边等多种接触形式共存，接触对和接触方向确定困难，数值模拟中易发生非物理的界面穿透.

迄今已有很多学者开展了动态接触算法研究[1-2]，但现有研究大多针对一般动态接触问题开展，侵蚀接触算法的研究还很少. BELYTSCHKO等[3]针对弹体穿甲问题以向量组装法自动识别/生成接触界面而构建了侵蚀接触算法，但没有讨论侵蚀接触中常遇到的接触对遗漏、多重接触等问题. WHIRLEY等[4]基于单元拓扑关系自动识别接触界面，采用“园管”和“小球”处理边、角接触，建立了自动接触搜索算法，但没有分析算法在侵蚀接触中应用. HEINSTEIN等[5]详细讨论了接触对确定、接触点计算及接触力施加方向不准确等问题，建立了用于接触对确定的静、动态检测算法；针对侵蚀接触给出了一种接触面自动生成/识别算法；采用接触强度方法处理多重接触问题，但该方法在处理尖角附近的接触时仍然可能会失效. 文中作者基于接触片间的面-面几何关系建立了可用于侵蚀接触计算的接触对确定方法[6]，但在接触深度计算中引入了很大的简化导致在某些复杂问题中计算精度降低. ZAVARISE等[7]讨论了二维准静态接触问题中接触对确定的三种歧义性并建议了多种处理算法. 然而，这些算法用于三维问题分析存在很大困难. 综之，目前为止侵蚀接触算法的研究还不充分，侵蚀接触计算精度仍需提高.

侵蚀接触计算可分解为4个步骤：接触界面自动生成/识别、接触对全局搜索、接触对局部搜索和接触约束施加. 其中，接触对全局搜索和接触约束施加算法与一般动态接触问题没有区别，具体算法可参阅相关文献[5,8,9]，这里不再赘述. 文中将重点讨论侵蚀接触计算中的接触对局部搜索方法，并给出接触界面的自动生成/识别算法. 需要说明的是，接触界面的点-面离散模型[9]仍是目前显式有限元程序最广泛采用的界面离散方法，而六面体单元是最常用的单元类型，因此文中侵蚀接触算法面向点-面离散模型、六面体单元间的接触计算设计. 文中接触约束施加采用罚函数法.

1 接触对确定

1.1 接触对预搜索

接触对全局搜索给出当前及随后若干时间步内系统中可能发生接触的部位(即接触测试对)，因此接触测试对集合通常远大于当前时间步内真实发生接触的(从点,主片)集合. 接触对局部搜索的目的就是从接触测试对中精确确定出当前时间步的真实接触对. 为提高计算效率，在接触对精确确定前引入“接触预搜索”以快速排除当前时间步内明显不会发生接触的测试对. 这里以“范围检测”和“法线检测”实现接触预搜索.

① 范围检测. 当前时间步，只有位于主片包围盒内的从点才可能与该主片接触. 主片的包围盒定义为以主片面心x0为球心，以长度l为半径的球形区域：

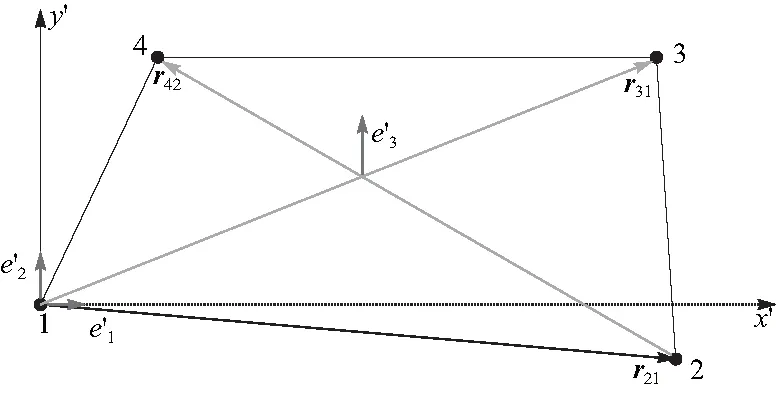
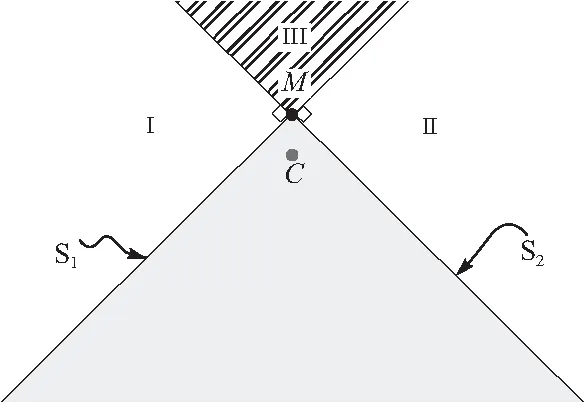
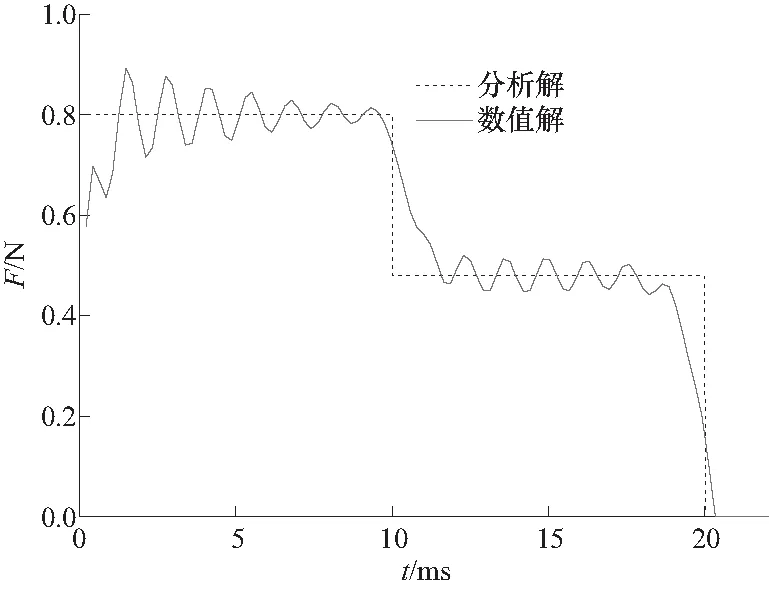
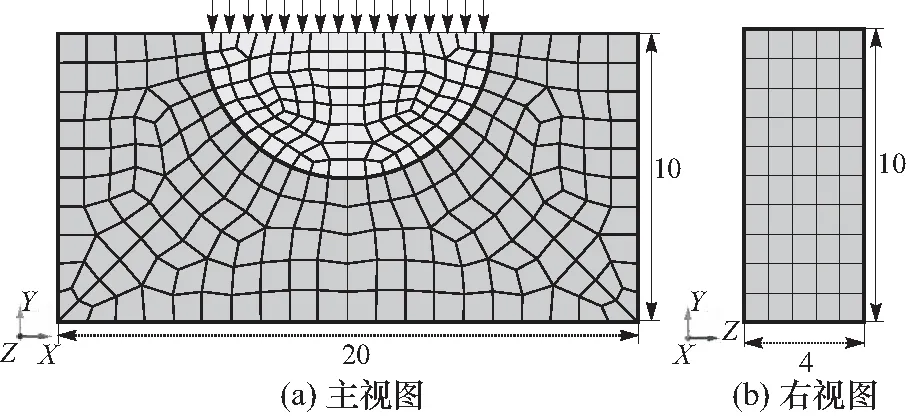
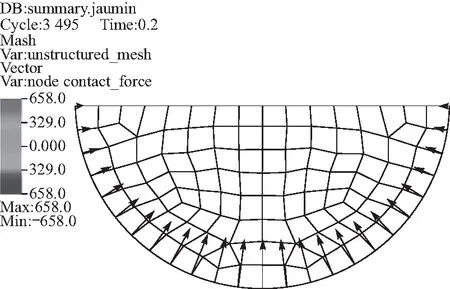
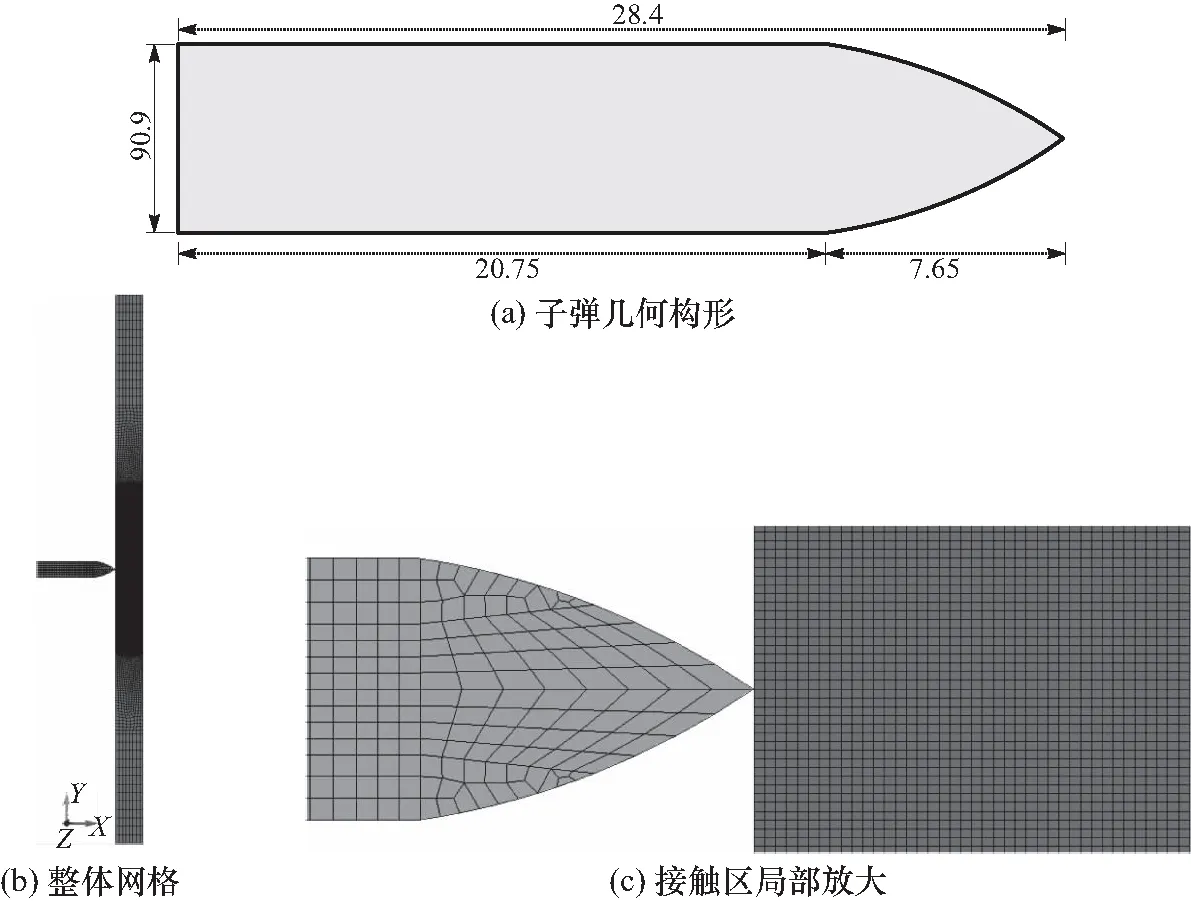
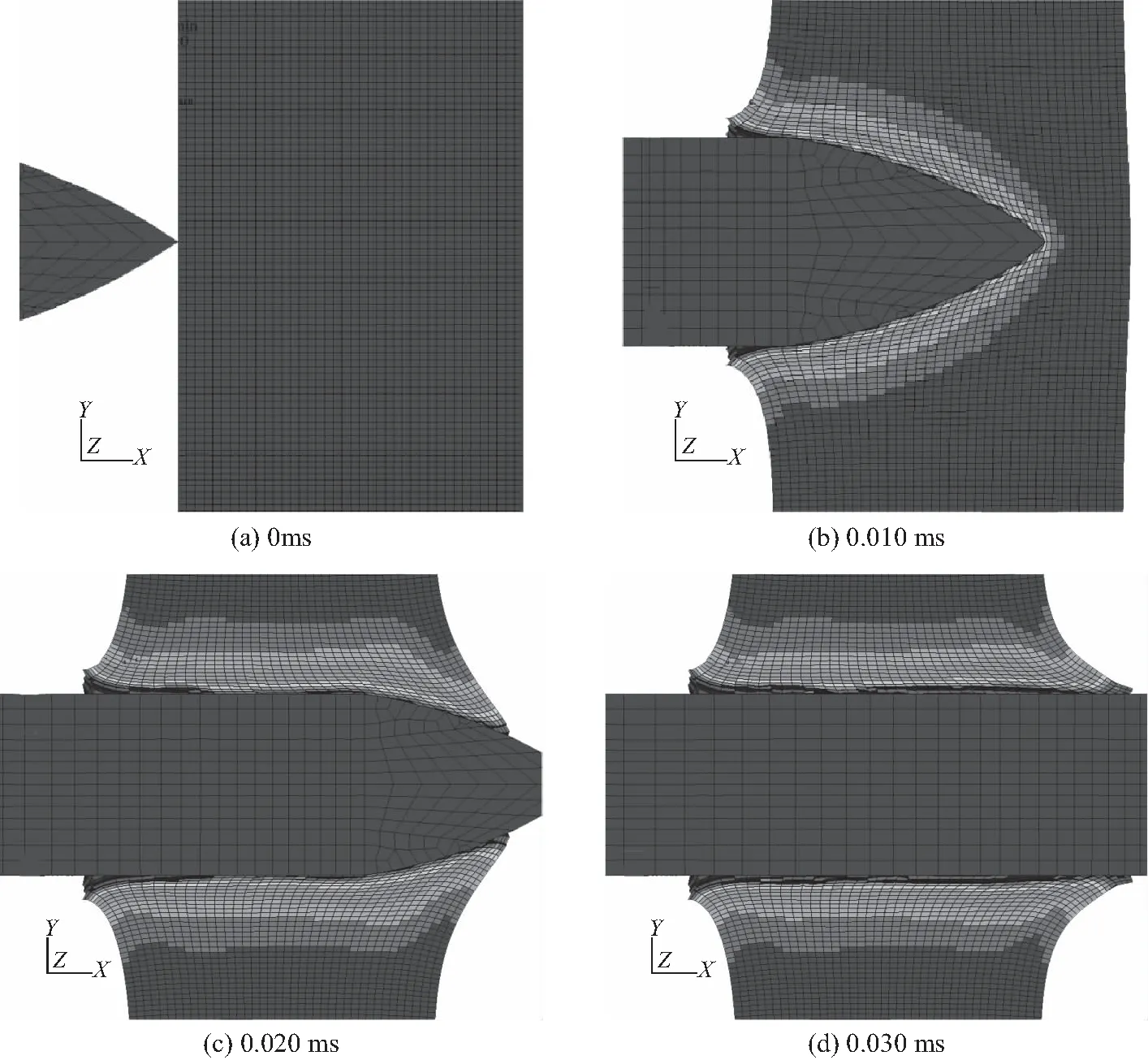
D={x|(x-x0)2

(1)

式中,l=max(l31,l42)，l31、l42为主片对角线的长度，下标1～4为主片节点的局部编号.

② 法线检测. 当从点与主片的外法线方向满足如下关系时，从点与主片才可能发生接触：

nm·ns<0

(2)

这里主片外法线方向nm近似为

(3)

从点法线方向ns定义为包含该节点的所有接触片外法线方向的加权平均值，即

(4)

式中：m为与从点相连的单元外表面数量;Ai为第i个单元外表面的面积.

1.2 接触对的确定

对于一个接触测试对，如果从点与主片满足：

① 从点在主片上的投影点位于该主片内；

② 从点与主片间的间隙函数值≤0.

则该测试对在当前时间步内为真实接触对；反之，从点与主片不会发生接触.

理想状态(单元规则且变形小)下，从点在主片上的投影点计算很简单，可利用牛顿迭代法求解下列方程组得到[4,10]：

(5)

但在冲击动力学问题中，单元常发生很大的变形、转动甚至扭曲畸变，接触片常变得很不规则，此时该方法存在计算量大、不稳定、收敛困难甚至不收敛等问题[8].

为克服牛顿迭代法计算投影点的困难，文中建立非迭代计算方法. 首先将接触从点、接触主片都投影到某个平面上，即将三维空间问题转化为二维平面问题. 投影面的构造如图1所示，投影面的基为

图1 投影面的构造

e′2=e′3×e′1

(6)

假定从点在投影面上的坐标为(x′,y′)，主片节点在投影面上的坐标为(x′i,y′i)，(i= 1～4). 以双线性插值描述主片，并建立局部坐标系统(r,s). 如果从点位于主片内，则从点坐标可表达为

(7)

(8)

式中:(r,s)为从点的局部坐标，(ri,si)为主片第i个节点的局部坐标. 将式(7)中消去s，可得关于r的二次方程：

Ar2+Br+C=0

(9)

这里A、B、C为与节点坐标相关的常数

A=a2b4-a4b2

B=a2b3-a3b2+a4(y′-b0)-b4(x′-a0)

C=a3(y′-b0)-b3(x′-a0)

(10)

以上各式中

a2=(-x′1+x′2+x′3-x′4)/4

a3=(x′3+x′4-x′1-x′2)/4

a4=(x′1-x′2+x′3-x′4)/4

(11)

式中,b0、b2等常数类似地由y′i给出. 利用二次方程的求根公式可计算出r,然后将r代入式(7)便得到s. 若计算出的从点局部坐标r、s位于区间[-1,1]，则从点对主片的投影就位于该主片内部.

知道了从点相对于主片的局部坐标(r,s)，便可容易地计算出从点与主片间的距离，即间隙函数值：

g=[xs-xc(r,s)]·nm

(12)

式中：xs为从点的坐标;xc为接触点(即投影点)的坐标.

1.3 特殊情况的处理

如果接触片规则、接触界面足够光滑，上述接触对确定方法可精确地给出接触对及其接触方向. 然而在侵蚀接触问题中，单元失效删除前通常会发生很大的变形或畸变，导致接触片很不规则；单元删除后会产生新的不规则接触片并存在大量尖角，导致接触界面极不平滑. 因此，侵蚀接触问题的数值模拟常存在接触对遗漏或接触方向不准确等问题，致使数值计算精度下降甚至错误.

1.3.1接触对遗漏

接触对遗漏包含两种情况. 第一种情况如图2(a)所示,即边界盲区问题，从点与主片边界接触，但数值计算出的投影点位于主片外. 这种情况主要是由于局部搜索算法引入的某些近似或者数值截断误差导致的. 此时可采用处理方法：引入一定的容差ε，适当放宽式(12)中投影点局部坐标(r,s)的取值范围：

图2 特殊情况的二维示意

|r|<1+ε,|s|<1+ε

(13)

数值计算经验表明，取ε=0.01～0.02可很好地解决绝大多数的接触对遗漏问题. 该方法实质上是对接触片引入一定的扩展域，抵消由于截断误差或投影点计算中近似处理(如不考虑接触片的翘曲、接触方向的近似等)引入的误差.

接触对遗漏的第二种情况如图2(b)所示，就是所谓的内盲区问题[9]. 由于采用罚函数法施加接触约束时，只有当从点穿透主片时才会施加接触力；另外，由于对接触片引入了式(13)形式的扩展，内盲区问题转变为多重接触问题.

1.3.2多重接触

多重接触即外盲区问题[9]如图2(c)所示，从点在多个主片上的投影点都位于相应主片内部，且其间隙函数值小于0. 此时，从点与多个主片都有可能接触，传统接触搜索算法[9-10]很难确定出真实的接触主片.

多重接触是侵蚀接触计算中的常见问题. 已有接触搜索算法[5,9,10]通常仅利用当前几何状态量确定从点与主片的接触关系，即使引入接触强度[5]也不能确定出真实接触对. 如图3所示尖角附近的接触，从点上一时间步由位置A穿透主片S1运动到位置B，当前时间步处于位置C. 如仅利用当前构形易得出从点穿透主片S2的错误结论. 因此，文中引入一个状态量跟踪从点对主片的穿透历史以便更好地确定接触对.

对每个从点I定义一个历史状态量state(I)记录该从点前一时间步接触的主片. 利用该状态量可以很容易地处理图3所示接触对确定的困难：如果state(I) = 1，表示从点穿透主片S1，即从点与S1构成接触对. 如果state(I) = -1，则表示前一时间步从点未与任何主片发生接触，而在当前时刻运动到位置C，如图4所示. 此时可按以下逻辑顺序和准则确定接触主片：

图3 基于当前构形确定接触对失效

① 计算从点对每个主片的侵彻深度(即间隙函数的负值)，选择侵彻深度小的接触片为该从点的接触主片；

② 如果从点对每个主片的侵彻深度相等，进一步计算接触强度nm·ns，并选择接触强度小的接触片为该从点的接触主片；

③ 如果接触强度相等，则从点是由区域Ⅲ中的某个位置运动到C的，接触点位于两个主片的公共边或公共点上，如图4所示的点M，接触方向为CM方向.

图4 存在多个潜在接触片时接触对的确定

2 算法设计

2.1 接触界面的自动生成与识别

侵蚀接触中，处于物体外表面的单元都有可能参与接触，因此每次全局接触搜索前需要首先确定出处于物体外表面的单元面作为全局搜索的输入. 显然，位于物体外表面的实体单元面只与一个单元相连，而位于内部的单元面与两个单元相连. 因此，可以利用单元面关联的单元数量确定该单元面是否属于外表面[4].

对于侵蚀接触，由于存在单元删除，单元拓扑结构生变化，位于外表面的单元面是动态变化的，因此必须设计合理的数据结构以满足接触片动态增减的需要. 文中利用为静态数组surface(I,i) 记录系统中所有单元面所连接的单元个数，I∈[1,ne]，i∈[1,6]，这里ne为系统中的单元数. 同时，对每个单元I定义一个状态量cellFail(I) 表征该单元的激活状态：如cellFail(I) = 1表示该单元失效，不参与接触计算. 如某个单元J失效，则对应的surface数组的J行所有元素值减1. 这样根据surface元素值可以方便地识别出处于物体外表面的单元面，实现接触面的自动生成/识别.

2.2 计算流程

文中侵蚀接触算法基于自主研发的并行显式有限元程序PANDA-Impact进行了实现，给出了每一个时间步内接触计算的伪代码.

3 算例分析

本节利用典型算例验证分析文中所建立的侵蚀接触算法的有效性. 算例一为经典的弹性杆碰撞问题[11]，用来验证接触点计算方法与程序实现的正确性；算例二为凹凸面间的接触问题[5]，分析文中算法处理多重接触问题的能力；第三个算例为弹体穿甲问题[12]，该问题涵盖了结构冲击响应数值模拟的所有非线性要素，如几何大变形、材料非线性等，用于综合验证文中侵蚀接触算法的有效性.

3.1 弹性杆对撞

如图5所示，方形截面杆A以1.0 mm/ms的速度对心撞击静止的方形截面杆B. 杆A与杆B截面积分别为1.0×106mm2、2.0×106mm2，长度均为1.0×104mm. 假定两杆材料均为弹性：杆A的弹性模量E=1.0×10-3MPa，B的弹性模量E=4.0×10-3MPa；两杆密度均为ρ=1.0×10-3g/mm3，泊松比υ均取为0.

由于两杆长度远大于其截面尺寸，又泊松比取为0，因此可以利用一维应力波理论计算出两杆撞击界面处的接触力F和界面速度v：

(14)

两杆都以20个单点积分六面体单元离散，见图5；两杆间的接触-碰撞作用以文中建立的侵蚀接触算法模拟. 图6给出了两杆碰撞过程中接触力F随时间t的变化曲线，图7给出了接触界面的速度曲线. 作为对比，图中同时列出了相应的理论解(由式(14)计算得到). 可以看出，虽然接触力和接触界面速度存在一定程度的震荡(这与OLDENBURG等[11]给出计算结果一致)，但其均值与理论解吻合良好. 总体上，数值方法较好地模拟了两弹性杆的碰撞过程,初步验证了接触点计算方法与程序实现的正确性.

图5 两弹性杆对撞的有限元网格模型

图6 接触力时程曲线

图7 接触界面速度曲线

3.2 凹凸面接触

如图8所示，半径为5.0 mm的半圆柱体在均布压力作用下向下运动挤压带凹槽(凹槽半径为5.0 mm)的方块体. 方块体底面及左右表面固支,半圆柱体上表面均布压力p随时间t变化：

图8 凹凸面接触计算模型

(15)

两物体材料均为弹性：半圆柱体密度ρ=8.0×10-3g/mm3，弹性模量E=2.0×105MPa，泊松比υ=0.3；方块体ρ=3.0×10-3g/mm3，E=7.0×104MPa，υ=0.3.

以单点积分六面体单元离散系统，网格剖分如图9所示，半圆柱体接触面(凸面)上的节点与方块体接触面(凹面)节点一一对应(相应节点坐标相同). 该问题模拟的难点在于，初始阶段凸面上的接触节点(顶点处的节点除外)处于凹面上接触片的内盲区；而对于凹面上的节点，它们则位于凸面上接触片的外盲区，每个节点存在多个潜在接触片. 该问题的正确模拟不仅要求接触搜索算法准确确定出接触对，更需要精确给出接触点与接触方向. 否则，系统中某些单元可能发生严重的畸变，半圆柱体甚至发生XY面内的大幅度转动或沿母线方向的滑移[5].

图9给出了文中算法的数值模拟结果(计算中应力的单位为MPa，力的单位为N). 可以看出，半圆柱和方块体上的单元变形均匀，系统的整体变形与应力分布关于YOZ面完全对称. 0.2 ms时刻半圆柱体接触界面上的接触力分布如图10所示(力的单位为N)，各节点接触力的大小与方向符合物理真实. 加载过程中，半圆柱体承受的接触力合力的如图11所示，接触力仅有Y向分量，圆柱体不会发生Z向滑动.

图9 0.2 ms时刻系统的变形

图10 0.2 ms时刻半圆柱体上的接触力

图11 半圆柱接触力时程曲线

3.3 弹体侵彻

7.62 mm尖卵形子弹以827.5 mm/ms的初速度侵彻10 mm厚度的靶板[12]，如图12所示，靶板长和宽都为200 mm，四周固支. 子弹与靶板材料的动态力学行为都以Johnson-Cook本构模型描述为

图12 计算模型

(16)

表1 子弹和靶板的材料参数[12]

考虑到系统的对称性，取1/2模型进行建模分析. 弹体和靶板都以单点积分六面单元离散，子弹单元的特征尺寸约为1.0 mm，靶板中间区域单元的特征尺寸约为0.2 mm，系统总单元数为409 264.

图13给出了子弹侵彻靶板过程中典型时刻的靶板变形及接触状态图像. 初始时刻弹尖处节点与靶板撞击面中心处节点接触(图13(a))，此时一个节点存在多个潜在接触片，需要接触算法给出合理的接触方向. 随着子弹侵入，靶板撞击面中心附近材料发生塑性大变形，当塑性应变达到失效应变时单元破坏删除，新生成的单元外表面继而与子弹接触. 此后，弹与靶板间的接触变得更加复杂：一方面由于部分单元失效破坏导致靶板上的接触界面存在大量尖角，极不平滑，如图14所示；另一方面接触面附近单元变形严重，这些因素导致接触对确定、接触点与接触方向计算存在很大难度. 但由图14可以看出，文中建立的侵蚀接触算法合理的模拟了该穿甲过程：侵彻过程中子弹受力对称，未发生偏转；靶板变形与破坏形貌与实验[12]一致.

图13 不同时刻的变形图像

图14 靶体接触界面形状

图15给出了侵彻过程中子弹的速度与加速度时程曲线，与类似子弹侵彻靶板文献[13]给出的数据在规律上完全一致. 子弹完全穿过靶板后，剩余速度为709 mm/ms，与实验数据702 mm/ms及Recht-Ipson模型理论理预测给出的710 mm/ms很接近.

图15 弹体的速度与加速度时程曲线

4 结 论

针对冲击动力学问题中存在单元破坏的动态接触-碰撞，即侵蚀接触问题，文中发展了一种可处理复杂接触界面的局部搜索算法. 新算法通过引入接触历史状态量跟踪从点对主片的接触历史，并结合接触强度确定真实接触对，有效克服了侵蚀接触计算中常遇到的接触盲区问题；在接触点计算中，发展了非迭代计算方法，提高了接触计算的稳定性.

利用弹性杆碰撞、高曲率凹凸面接触、弹体穿甲等典型算例验证了文中算法的有效性. 算例分析表明，文中建立的侵蚀接触算法可有效实现侵彻接触问题的数值模拟，可用于复杂动态接触问题分析并具有较高的计算精度.