两种感染途径和接种的出血热模型稳定性分析*
李凤, 刘俊利
(1.西安医学高等专科学校,陕西 西安 710309;2.西安工程大学,陕西 西安 710032)
1 前言
汉坦病毒生存并繁殖在鼠类体内,也在鼠类之间传播,然而感染这种病毒的鼠类没有任何的症状和明显病变,但是人类若感染这种病毒便会导致流行性出血热[1-3].人类被感染的主要方式是被鼠类直接咬伤或误食被鼠类排泄物污染的食物,它的潜伏期一般为2周左右[4-5],且可通过自然感染获得动态的免疫屏障(即感染过的人不会再次感染).目前医学上已研制出出血热疫苗,人类可以通过接种获取90%以上的保护率.
传染病数学模型可以为传染病的发展及控制提供理论依据.2002年,Abramson和Kenkre提出了一类汉坦病毒鹿鼠模型,分析了汉坦病毒在鼠种群间的传播[6];2003年,他们又提出了带有反应扩散的汉坦病毒模型,表明环境参数控制着两种传播方式间的过渡[7].2017年,姜黎和姚美萍基于国内疫情防护措施,建立了一类人鼠耦合汉坦病毒模型,得出加强防控措施可对其进行控制的结果[8].结合前人的研究,本文在考虑染病鼠对易感人群和鼠群直接传播[9]的同时加入了接种因素,并对模型的局部稳定性及持久性进行了分析.
2 模型建立
根据汉坦病毒的传播途径并考虑接种因素,给出仓室图(见图1),并建立模型

图1 模型仓室图
(1)
其中,SH、IH和RH表示t时刻人群中的易感者数量、染病者数量和恢复者数量(即SH(t)、IH(t)和RH(t)),SH+IH+RH为总人数;SM和IM表示t时刻易感鼠和染病鼠的数量(即SM(t)和IM(t));x表示t时刻具有传染性的出血热病毒数量(即x(t));A1和A2分别表示人和鼠的输入率;β1和β2分别表示人群中易感者被染病鼠类咬伤和被环境中出血热病毒感染的传染率;ρ表示易感者的疫苗接种率;σ表示感染了出血热病毒后人的恢复率系数;β3和β4分别表示易感鼠被染病鼠类咬伤和被环境中出血热病毒感染的传染率;a表示染病鼠的出血热病毒释放率;d1和d2表示人和鼠的自然死亡率系数;病毒离开寄体后的消亡率系数用d3表示.
假设模型(1)的所有解均满足初值条件
SH(0)>0,IH(0)>0,RH(0)>0,SM(0)>0,IM(0)>0,x(0)>0.
(2)
对于任意常数ε>0,定义
当t充分大时,模型(1)的全部正解满足初始条件(2),且进入或停留在区域Γε中,因此本文只在Γε中考虑模型(1)的动力学性质.
3 基本再生数与平衡点的局部稳定性
显然模型(1)有唯一无病平衡点E0=(SH0,0,RH0,SM0,0,0),这里
根据基本再生数计算方法[10],定义
则有
基本再生数由ρ(FV-1)给出,经计算得
其中
且令R01=C0+C1,易得R0-1与R01-1符号相同.

显然,只有R01>1时,R0>1,此时模型(1)有唯一的地方病平衡点E*.
定理1如果R0<1,则无病平衡点E0局部渐近稳定; 如果R0>1,则E0不稳定.
证明模型(1)在E0处的雅可比矩阵为
则E0处的特征方程为
(3)
显然(3)有四个负实根,令上式中的行列式为零,展开得
(4)
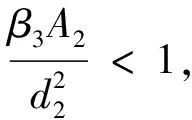
定理2如果R0>1,则地方病平衡点E*局部渐近稳定.
证明模型(1)在E*处的雅可比矩阵为
则E*处的特征方程为
(5)
其中
计算得

由Routh-Hurwitz判据[11]可知,(5)的所有解均有小于零的实部,所以当R0>1时,E*局部渐近稳定.
4 疾病的持久性

引理1[10]若R0>1⟺r(F-V)>0,若R0<1⟺r(F-V)<0.
定理3若R0>1,则模型(1)是持久的,即存在常数η>0,使得模型(1)具有非负初值条件且IH(t)+IM(t)+x(t)>0的解(SH(t),IH(t),RH(t),SM(t),IM(t),x(t))满足
证明定义X={(SH,IH,RH,SM,IM,x)∈Γε},X0={(SH,IH,RH,SM,IM,x)∈X∶IH+IM+x>0},∂X0=XX0={(SH,IH,RH,SM,IM,x)∈X∶IH=IM=x=0}.
下证对于(X0,∂X0),模型(1)是一致持久的.
易证X和X0是模型(1)的正向不变集,设B是它的一个列紧集,则它的解从X中出发最终进入B.关于X的紧度条件(C4.2)也很容易验证[13].
定义M∂={(SH(0),IH(0),RH(0),SM(0),IM(0),x(0))∶(SH(t),IH(t),RH(t),SM(t),IM(t),x(t))∈∂X0,t≥0}.下证
M∂={(SH,0,RH,SM,0,0)∶SH≥0,RH≥0,SM≥0}.
(6)
设(SH(0),IH(0),RH(0),SM(0),IM(0),x(0))∈M∂.只需要证明∀t≥0,IH(t)=IM(t)=x(t)=0.设存在t0≥0,使得IH(t0)>0或IM(t)>0或x(t0)>0,则(SH(t0),IH(t0),RH(t0),SM(t0),IM(t0),x(t0))∈X0,与(SH(0),IH(0),RH(0),SM(0),IM(0),x(0))∈M∂矛盾,(6)得证.
令Ω=∪{ω(SH(0),IH(0),RH(0),SM(0),IM(0),x(0))∶(SH(0),IH(0),RH(0),SM(0),IM(0),x(0))∈M∂},ω(SH(0),IH(0),RH(0),SM(0),IM(0),x(0))是以(SH(0),IH(0),RH(0),SM(0),IM(0),x(0))为初值的模型(1)解的ω极限集.限制系统(1)在M∂上得
(7)

其中(SH(t),IH(t),RH(t),SM(t),IM(t),x(t))是初值在X0中的任意解,根据Leebheer和Smith的引理3.5[14],只需证明WS(E0)∩X0=∅,其中WS(E0)是E0的稳定流形.
假设WS(E0)∩X0=∅不成立,则当t→∞时,在X0中存在一个解(SH(t),IH(t),RH(t),SM(t),IM(t),x(t)),有
SH(t)→SH0,RH(t)→RH0,SM(t)→SM0,IH(t)→0,IM(t)→0,x(t)→0.
(8)
当R0>1时,对足够小的δ>0,存在T>0,当t>T时有
SH0-δ SM0-δ 0≤x(t)<δ,IH(t)+IM(t)+x(t)>0. 当t>T时,由模型(1)可得 即 构建了在两种传播途径的基础上加入接种因素的出血热模型,计算了模型的无病平衡点和基本再生数R0,利用Routh-Hurwitz判据等判断了模型平衡点的局部稳定性,如果R0<1,E0局部渐近稳定,疾病灭绝;如果R0>1,E*局部渐近稳定.证明了R0>1时流行性出血热的持久存在性.由R0的表达式知灭鼠和环境管理相结合对控制出血热的传播起着至关重要的作用.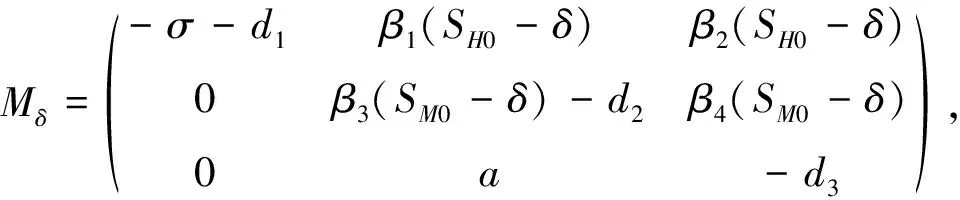
5 结语

