基于实测误差的齿轮传动模型的建立与分析
苏家乙,王德伦
(大连理工大学机械工程学院, 辽宁大连 116024)
0 引言
齿轮传动是机械传动中最常见的形式之一,广泛应用于各类机械设备和仪器仪表中。齿轮传动的质量对设备的精度、寿命、振动和噪声等有重大影响,而齿面接触区域和齿轮传动误差是衡量齿轮传动质量好坏的综合技术指标[1]。因此,研究各类误差下齿轮传动的情况有重要的意义。
使用计算机模拟齿面接触传动的方法称为齿面接触分析技术(Tooth Contact Analysis,TCA)。美国Livtin[2]总结了TCA技术,并普遍应用于不同的齿轮啮合。郑启昌[3]、方宗德[4]、蒋进科[5]利用TCA技术对准双曲面齿轮、弧齿锥齿轮、直齿轮和斜齿轮等进行接触分析,并讨论了齿面误差、修形和安装误差对传动的影响。考虑误差时齿轮副传动退化为空间中两刚体接触传动,齿面上的点、线、面都可能参与接触导致边缘接触等情况。然而现有研究中并未对接触类型进行有效辨识进而形成统一模型,导致对考虑误差时的齿轮传动情况分析不准确。
综上,本文以渐开线直齿轮为例,基于齿面误差、齿距误差和轴线误差测量原理,依据基本的运动几何学理论建立齿轮传动模型,对考虑上述误差时齿轮的传动情况进行分析。
1 基于误差测量原理的模型构造
1.1 齿面误差的测量原理及模型处理
对渐开线直齿轮,一般采用双基圆盘式渐开线测量仪测量其横截面上的齿面误差,其具有测量结构简单、测量精度高与经济性好等特点[6]。齿面误差的测量原理如图1所示。当齿面为渐开线时,杠杆测头轨迹为渐开线,杠杆输出值为0;当齿面存在误差时,杠杆测头会移动,移动的距离为误差齿廓与渐开线在AP方向的差值,即测量得到渐开线法线方向的误差值。

图1 齿面误差测量原理示意图
使用测量仪进行多次测量,可得到若干端面的齿面误差值,将这些离散误差值通过拟合得到误差曲面e(u,v)。将误差曲面按照测量原理,即沿渐开线法线方向叠加到理想齿面上即可得到考虑齿面误差的真实齿面,则有

式中:R为真实齿面方程;R0为理想齿面;n0为理想渐开线的单位法矢;u、v为曲面参数。
已知真实齿面的解析方程,其法矢量N为

1.2 齿距误差的测量原理及模型处理
在国家标准中,齿距误差有多种评价指标,有单个齿距误差fpt、齿距累计误差Fpk和齿距累计总误差Fp[7]。单个齿距误差fpt的定义为:在端平面上接近齿高中部的一个与齿轮轴线同心的圆上,实际齿距与理论齿距的代数差。
从建立齿轮几何模型的角度,只需已知fpt即可确定各个齿面之间的关系。绝对测量法的测量原理与fpt的定义一致。在模型中通过改变相邻齿面的夹角来反映齿距误差,如图2所示。

图2 模型中fpt的处理
已知齿面上某齿面的方程RZ1,则考虑齿距误差的相邻齿面的方程为
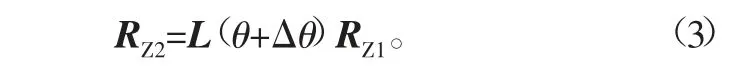
式中:L为旋转矩阵;θ为理论齿距对应的旋转角,有θ=2π/z;Δθ为齿距偏差fpt对应的旋转角,有Δθ=fpt/rpt。
1.3 轴线误差的测量原理及模型处理
在课题组研究[8]的基础上,通过双标准球和编码器测量得到齿轮轴线的6自由度运动,测量原理如图3所示。
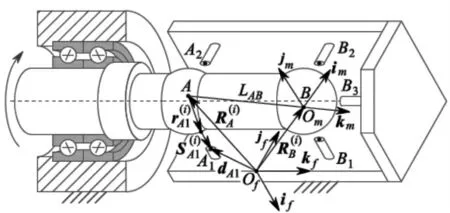
图3 轴线误差测量原理图
根据测量原理图可建立闭环矢量方程:


由于轴线的位姿由测量得到,轴线每个转角位置的位姿都已知,所以在模型中把轴线除转角外的5自由度运动拟合为转角φ的函数,即在模型中轴线为单自由度6维度运动。
2 齿面接触传动
2.1 单对齿面接触传动
由于要对考虑误差时齿轮接触的运动进行描述,首先建立固定坐标系Sf、两齿轮轴线坐标系Se1和Se2、两齿轮坐标系Sh1和Sh2,结果如图4所示。

图4 齿轮传动模型的坐标系
考虑误差时,齿面上的点、线、面都有可能参与接触,所以需要对接触类型进行辨识从而选择合适的接触方程并求解。在本文中,总结各种接触的情况,将齿面分为6个区域,如图5所示。根据基本的几何关系,使两齿面在理想啮合位置的基础上,相对转动一微小角度,求解此时两齿面上距离最近的两点,根据两点在齿面上所在区域即可得到此时的接触类型。

图5 齿面分区示意图
在本文中假设齿轮1齿宽大于齿轮2齿宽,分析得到可能出现的接触情况如下:
1)齿轮1齿顶A3与齿轮2下端面曲线B4接触:


式(6)~式(14)中:R1、R2为两齿面位矢;n1、n2为两齿面法矢;L为旋转矩阵;M为齐次变换矩阵;φ1、φ2为两齿轮转角;u1、v1、u2、v2为两曲面参数。
在模型中,给出齿轮1的转角φ1,在Matlab中可编程求得与其接触的齿轮2转角和接触点。
2.2 多对齿面接触传动
通过上节处理,能够完成单对齿面的接触分析,接下来讨论多对齿面交替传动的情况。在一对齿轮传动过程中,每个时刻至少有一对齿面接触传递运动,不妨将其称为主导齿面。根据运动几何学理论,当多对齿面共同接触时,转速快的齿面主导运动,其余齿面会被顶开,如图6所示。
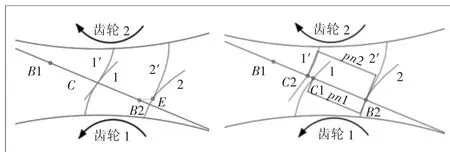
图6 主导齿面变化的示意图
在模型中,若出现多对齿面同时接触,将这多对齿面分别进行下一时刻的齿面接触分析,从动轮相对转角最大的齿面作为主导齿面。经过上述处理,能够准确地模拟齿轮交替时的边缘接触情况。
3 算例分析
以一对标准渐开线直齿轮为例,各基本参数如表1所示。通过测量得到各误差值,齿轮齿面误差如图7所示,齿距误差如图8所示,轴线误差如图9所示。使用Matlab编写模型程序,计算得到齿轮的传动误差和齿面接触情况。
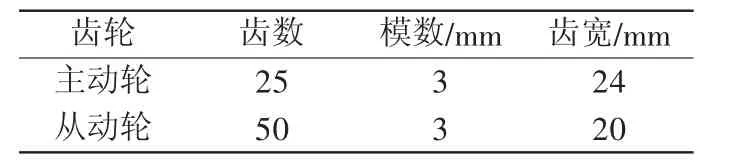
表1 齿轮参数
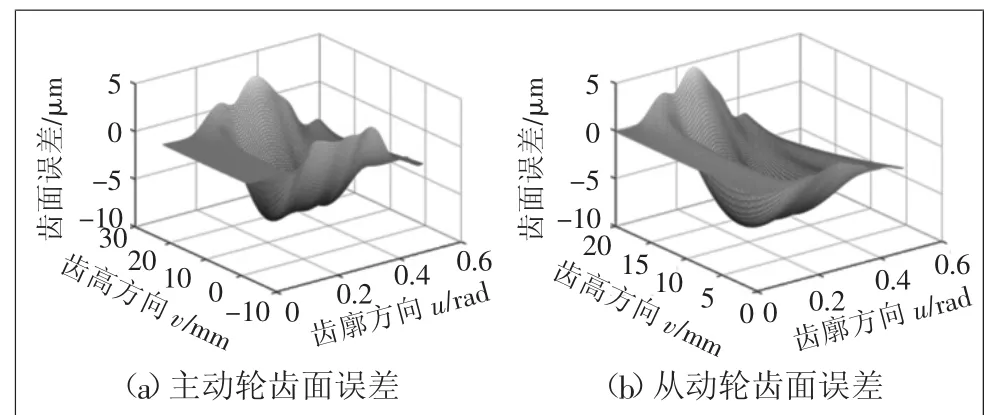
图7 齿面误差曲面
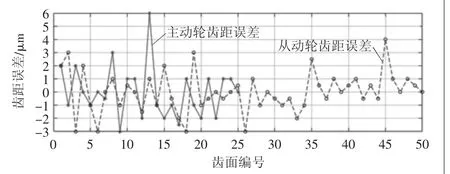
图8 齿距误差

图9 轴线运动误差
3.1 考虑齿面误差时的齿轮传动分析
假设各齿面的齿面误差相同,模型计算结果如图10~图12所示。将所有接触点在固定坐标系下描述,如图10所示,可以发现接触点集中在中部,即所有齿面基本在齿面中部接触传动,这是由于按照给定的齿面误差(如图7)构造的真实齿面中凸造成的。任取一对啮合齿面,其接触情况如图11所示。从图12可知,齿面误差会产生小幅度波动状的传动误差。

图10 考虑齿面误差时的啮合线
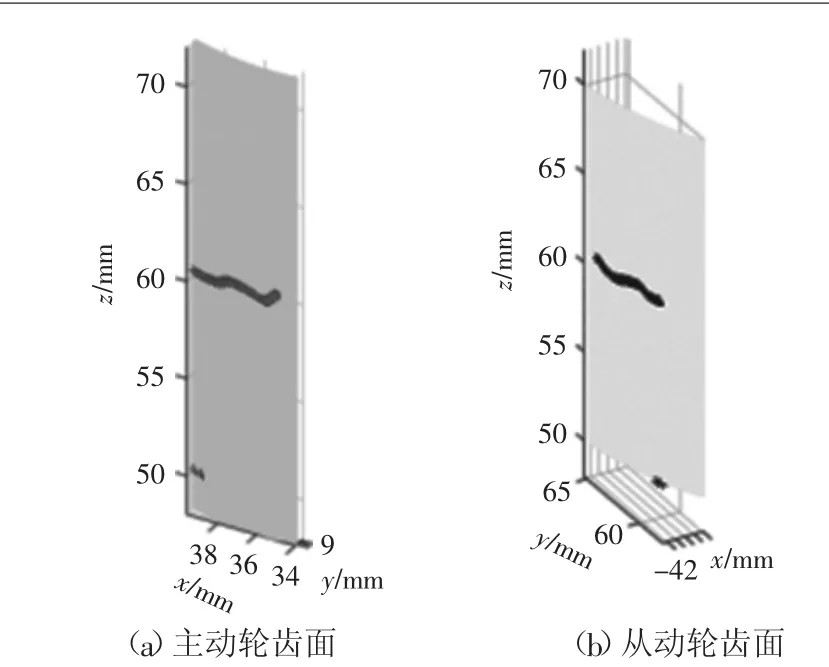
图11 考虑齿面误差时的齿面接触情况

图12 考虑齿面误差时的传动误差
3.2 考虑齿距误差时的齿轮传动分析
考虑齿距误差时,模型的计算结果如图13~图15所示。将所有接触点在固定坐标系下描述,如图13所示,可知存在齿距误差时,啮入-啮出处的接触点偏离理论啮合面,这是由于此时发生了齿顶刮着齿面传动的情况,产生速比冲击。任取一对啮合齿面,其接触情况如图14所示,可知主动轮齿根部分与从动轮齿顶部分未参与接触,这是因为前一对齿面接触后,由于存在齿距误差,此对齿面未能正常进入啮合。从图15可知,齿距误差会在齿面啮入-啮出时产生类弦函数的传动误差。
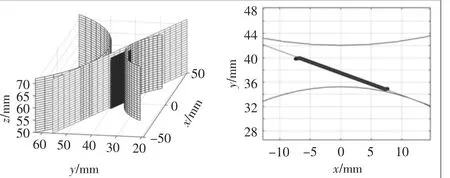
图13 考虑齿距误差时的啮合面
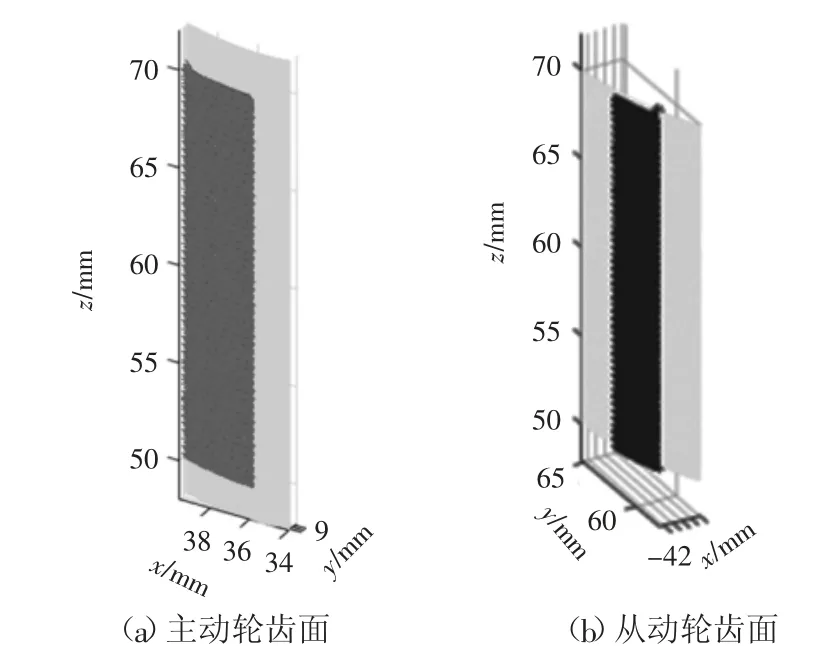
图14 考虑齿距误差时的齿面接触情况

图15 考虑齿距误差时的传动误差
3.3 考虑轴线误差时的齿轮传动分析
考虑轴线误差时,模型的计算结果如图16~图19所示。将接触点放到固定坐标系中描述,如图16所示,可知接触点主要集中在两端,中间区域有少量离散接触点,这是因为考虑轴线误差时,主要发生从动轮端面曲线与主动轮齿面相切接触的情况。任取一对啮合齿面,将其接触点放到齿轮坐标系中描述,得到齿面接触情况,如图17所示。从图18可知,轴线误差会引起大范围波动的传动误差。也可对齿轮转角数据进行离散求导,得到速比计算结果如图19所示。
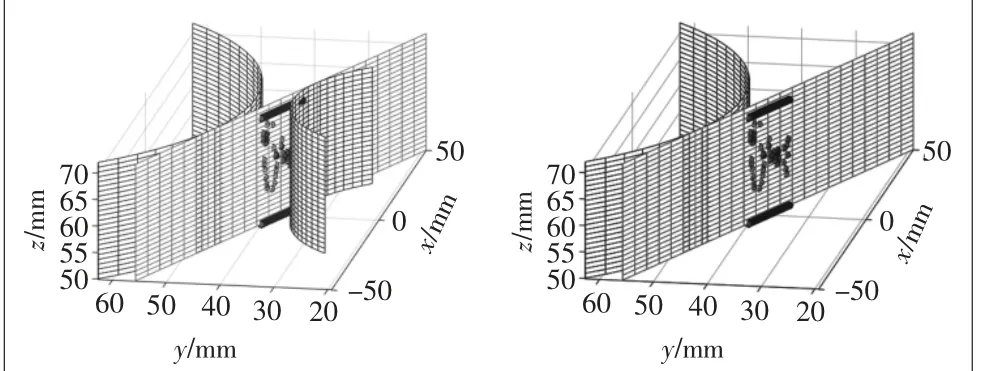
图16 考虑轴线误差时的啮合面
4 结语
以渐开线直齿轮为例,基于误差测量原理,依据基本的运动几何学理论建立齿轮传动模型,能够准确实现齿轮传动的几何分析。通过算例分析可知:齿面误差会导致小范围波动的传动误差,影响齿轮传动的平稳性;齿距误差会使齿面在啮入啮出处产生线外接触,造成速比冲击,导致类似弦函数的周期传动误差,从而使齿轮副产生噪声;轴线误差会使齿面在一端接触,不利于齿面载荷分布,导致大范围波动的传动误差。由于本模型是根据运动几何学理论建立的,可推广应用到其他类型齿轮传动机构的分析中。
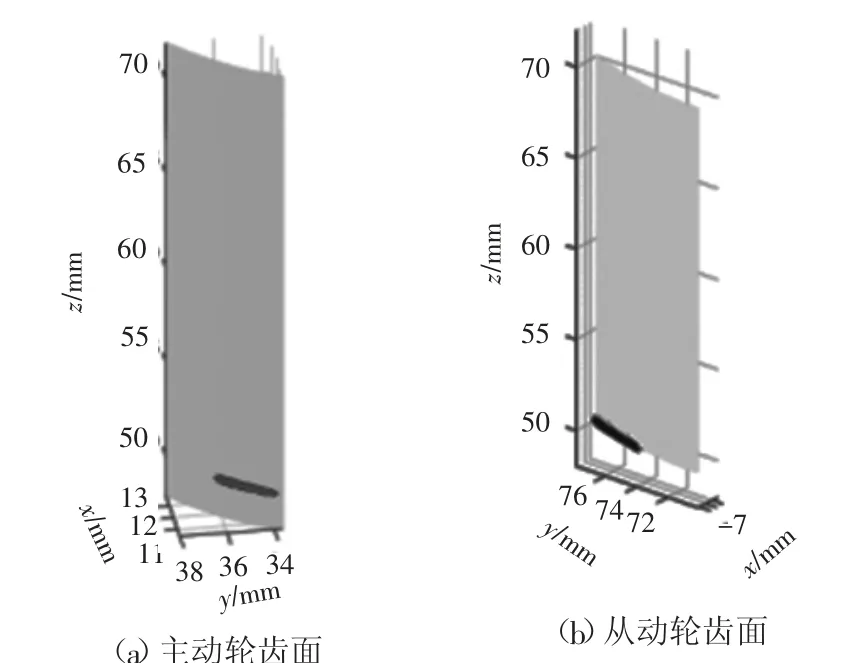
图17 考虑轴线误差时的齿面接触情况

图18 考虑轴线误差时的传动误差

图19 考虑轴线误差时的速比

