具有敏感边缘权重的加权社会网络匿名算法
毕红净,卢立蕾
计算机科学与自动化技术
具有敏感边缘权重的加权社会网络匿名算法
毕红净,卢立蕾
(唐山师范学院 计算机科学系,河北 唐山 063000)
针对大型数据网络隐私保护问题,首先构造了一个k-度匿名网络。为保证发布数据的可用性,提出了贪心边权重扰动(GEWP)算法,该算法通过发布网络数据时扰乱某些边缘的权重防止隐私泄露,同时保留原始网络中敏感节点对之间最短路径和路径的长度。仿真实验显示的结果和理论分析相符合。
加权社会网络;敏感边缘权重;K-匿名;隐私保护
1 引言
社会网络是由实体以及连接实体的边组成的特殊图形结构。实体或节点表示用户,连接实体的边缘表示这些用户之间的关系或交互。连接实体之间的边可用来表示金融交换、朋友关系、冲突可能性、网络链接、疾病传播(流行病学)等。第三方发布数据集之前,数据所有者必须保证用户隐私信息不被泄露,因此,社会网络图的匿名化过程成为一个重要的问题。Ferri等人[1]的研究表明,尽管有一些用户群体不介意数据拥有者共享数据,但高达90%的成员不同意这个原则。Backstrom等人[2]指出,发布实际网络之前,删除顶点的身份来匿名网络的简单技术并不能保证用户的隐私不被泄露。事实上,攻击者可以通过一些背景知识来推断用户的隐私信息。因此,为保护机密、敏感和安全信息不被披露需要加快社会网络隐私保护技术的发展,这就需要在保护机密信息和最大化社会网络的效用分析之间进行最佳权衡。
为了保护隐私,在不公开原始数据并且保证数据分析结果尽可能接近原始数据的前提下,已经发布了各种技术。k-anonymity模型是最具代表性的隐私保护方法。k-anonymity模型表明虽然攻击者设法找到与匿名数据集中出现的用户相关的外部知识,但是不能区分不同的k个记录或个人,因此,攻击者不能重新识别概率大于1/k的个体。k-度匿名的主要目标是所有顶点至少有k-1个其它顶点共享相同的度数。Salas等人[3]提出了一种k-degree匿名方法,保证每个近似值在度序列中至少有k个元素,当匿名度序列的度数之和为偶数时,使用欧几里德距离得到k-degree匿名的最优解。LiuK等人[4]提出无向图匿名概念,利用贪心策略增加边的方法实现匿名,抵御节点度攻击。Casas等人[5]提出UMGA算法实现K-度匿名。Chester等人[6]也考虑了k度匿名问题,但是通过在假顶点和假顶点之间添加新的边来修改网络结构。Bhattacharya等人[7]提出了一种迭代算法来生成给定社会网络图的k-匿名顶点度序列,以保护图免受被动攻击。Hartung等人[8]提出动态规划和启发式方法实现k-度匿名,提高处理大规模社会网络无向图的效率。Li Y等人[9]提出随机稀疏化和随机扰动化的手段,使用概率的方法对社会网络无向图进行随机修改。Tsai等人[10-11]提出了基于加权社会网络的k-匿名保护方法,添加和删除社会网络中的加权边缘,防止攻击者根据度数信息重新识别节点。基于层次社会机构,张晓琳等人[12]提出了一种保护链接关系的分布式匿名算法PLRD-(k,m),既保证了数据的可用性,又不让攻击者通过度和标签识别出目标个体。
2 背景知识与问题定义
定义1(加权社会网络图)用G={V,E,W}表示一个加权社会网络图,其中V={vi|1≤i≤n},为图G中节点个数,V(G)为图G的节点集;E={ei,j},ei,j表示节点的边,E(G)为图G的边集;W={wi,j},wi,j为边ei,j的权重,W(G)为图G的边权重集合。

图1 加权社会网络图

定义3(匿名度序列)如果度序列中不同节点的度数出现至少k次,则该度序列是k-匿名的,用d~表示。
定义4(匿名加权社会网络图G~)用G~ ={V~,E~,W~}表示一个匿名加权社会网络图,如果节点匿名度序列满足k-度匿名,那么G~也是k-度匿名的。
定义5(敏感节点对) 用H表示敏感节点对(si,sj)的集合,其中si,sj∈V。敏感节点对是指需要保留节点对之间的最短路径psi,sj以及相应的路径长度dsi,sj,并使匿名后的路径长度尽可能的与原始路径长度保持一致。
定义6(未访问边NV)对于∀(si,sj)∈H,如果evi,vj∉psi,sj均成立,那么边evi,vj为未访问边缘,即所有敏感节点对的最短路径均不经过未访问边缘。
定义7(全访问边AV)对于∀(si,sj)∈H,如果evi,vj∈psi,sj均成立,那么边evi,vj为全访问边缘,即所有敏感节点对的最短路径均经过全访问边缘。
定义8(部分访问边PV)对于∀(si,sj)∈H,(sk,sl)∉H,如果evi,vj∈psi,sj,evi,vj∉psk,sl,那么边evi,vj为部分访问边缘,所有敏感节点对的最短路径只有一部分经过部分访问边缘。
如图1所示的加权社会网络图G,假设敏感节点对H={(1,7),(3,7),(5,7)},pv1,v7=e12,e26,e67,pv3,v7=e32,e26,e67,pv5,v7=e56,e67,根据前面定义可得:
NV={e13,e34,e25,e57}
AV={e67}
PV={e12,e26,e32,e56}
2.1 k-度匿名算法
首先以原始网络G的度序列d-={d-1,...,d-n}为基础,构造一个k度匿名序列d~={d1~,...,dn~}。使用函数Δd表示从匿名度序列到原始度序列的距离,计算公式为:
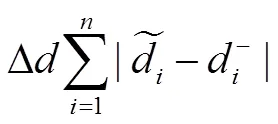
Δd的值越低,则匿名网络的信息损失就越低。
然后,利用基本的边修改操作,构造一个新的网络G~=V~,E~),其度序列等于d~。这些操作允许根据匿名化程度序列(d~)修改网络结构。添加的虚拟边的权重赋值为原始图中最大权重值。图的修改有三种基本操作:边转换、边添加和边删除。
边转换:如果(vi,vk)∈E和(vj,vk)∉E,可以删除Vj(vi,vk)并连接(vj,vk)。如图2(1)显示了这个基本操作。边转换操作对度序列的影响为di~=di-1和dj~=dj+1,操作前后网络图中边缘的数量保持不变,vi的度数减1,vj增加1,vk保持相同的度数。
边添加:选择两个顶点vi,vj∈V,其中(vi,vj)∉E并创建它。边添加操作对度序列的影响为di~=di+1和dj~=dj+1,如图2(2)所示。
边删除:选择四个顶点vi,vj,vk,vl∈V,其中(vi,vk)∈E,(vj,vl)∈E,(vk,vl)∉E。删除(vi,vk)和(vj,vl)之间的边并添加一个新的边(vk,vl),如图2(3)所示。边删除操作对度序列的影响为di~=di-1,dj~=dj-1,dk~=dk和dl~=dl。
对于匿名度序列用向量δ=d~-d表示哪些结点需要改变度数,δ表明哪个顶点必须增加或减少其度数才能达到所需的k-度匿名。使用图2中描述的三种基本操作对图进行修改,得到需要减少其度数的顶点列表δ-={vi:δi<0},需要增加的顶点列表δ+={vi:δi>0}。

图2 3种基本边操作
因为要保持敏感节点对之间的最短路径psi,sj以及相应的路径长度dsi,sj不变,还要使匿名后的路径长度尽可能与原始路径长度保持一致,因此,在图修改过程中只能选择对敏感节点对路径没有影响的边,即只能对未访问边缘进行基本边操作,而对部分访问边缘和全访问边缘不能进行边删除或边转换操作。另外,对于加权社会网络,新添加边的权重设置为原始图中最大的权重值。
2.2 最短路径保持的贪心边权重扰动(GEWP)算法
k-度匿名算法保护了加权社会网络图结构信息,满足图结构的k-度匿名。假定社会网络中所有节点对的最短路径并非都被认为是重要的,敏感节点对是由数据的拥有者设置的,也就是说数据拥有者决定哪条最短路径需要被保护,哪一条不需要被保护。在数据拥有者的约束下,为实现最大程度保留图的权重信息、尽量保证原始图与扰动图的信息不变,我们提出了最短路径保持的贪心边权重扰动(GEWP)算法。GEWP算法在扰动期间保持敏感节点对的最短路径相同,并且保持扰动的最短路径长度接近原始路径的长度,这样得到的匿名网络图满足以下条件:
V*=V,E*=E (1)
对于∀(si,sj)∈H

在社会网络G={V,E,W}(||V||=n)中,生成最短路径列表集P和相应的n*n长度邻接矩阵D,每个条目psi,sj是表示si和sj之间的最短路径的链表(即si和sj分别是最短路径的开始和结束节点)。例如,p1,7=(v1→v2→v6→v7),表明最短路径p1,7连续通过v1,v2,v6和v7。在邻接矩阵D中,每个dsi,sj是连接si和sj的最短路径的长度。

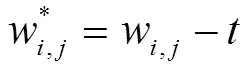

图3 扰动未访问边缘和全访问边缘
社会网络中,非访问边缘和全访问边缘的权值可以显著改变,而不影响H中的任何最短路径,因此算法主要扰动部分访问边缘PV。为了最小化原始最短路径的长度与相应的扰动最短路径的长度之间的差异,在PV边上提出了两个扰动方案。如果扰动最短路径的当前长度大于原始最小路径的当前长度,可以减少此路径中一条边的权重。否则,需要增加它的权重,以保持扰动的最短路径的长度接近原始路径。
2.2.1 增加扰动边缘权重

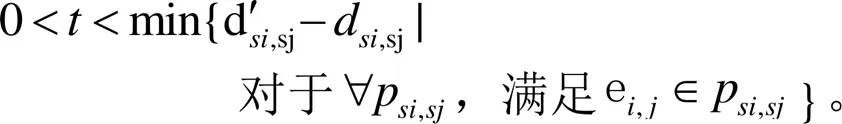

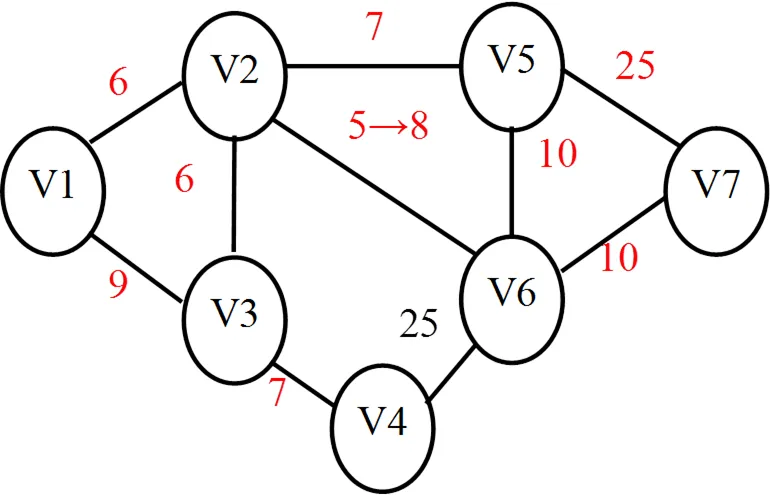
图4 增加部分访问边缘权重

其中
2.2.2 减少扰动边缘权重
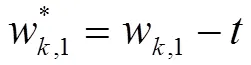
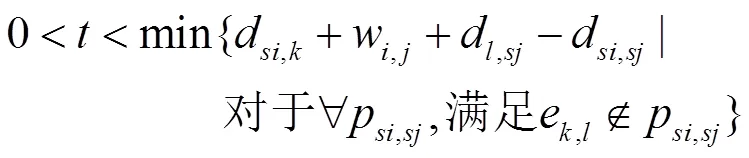
扰动前后所有敏感节点对的最短路径,部分路径长度。

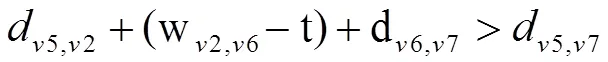
3 实验结果与分析
实验创建1 000个节点的合成数据集G,其对应的邻接矩阵是1 000*1 000对称矩阵。边缘权重设定0-50的随机数,当其权重为0时,则表示两节点不连通。假设数据集中20%敏感节点对H,利用Bellman-Ford算法计算敏感节点对的最短路径并得出其长度,遍历所有最短路径经过的边,找出部分访问边缘进行扰动策略,实现匿名。实验结果如图6所示。
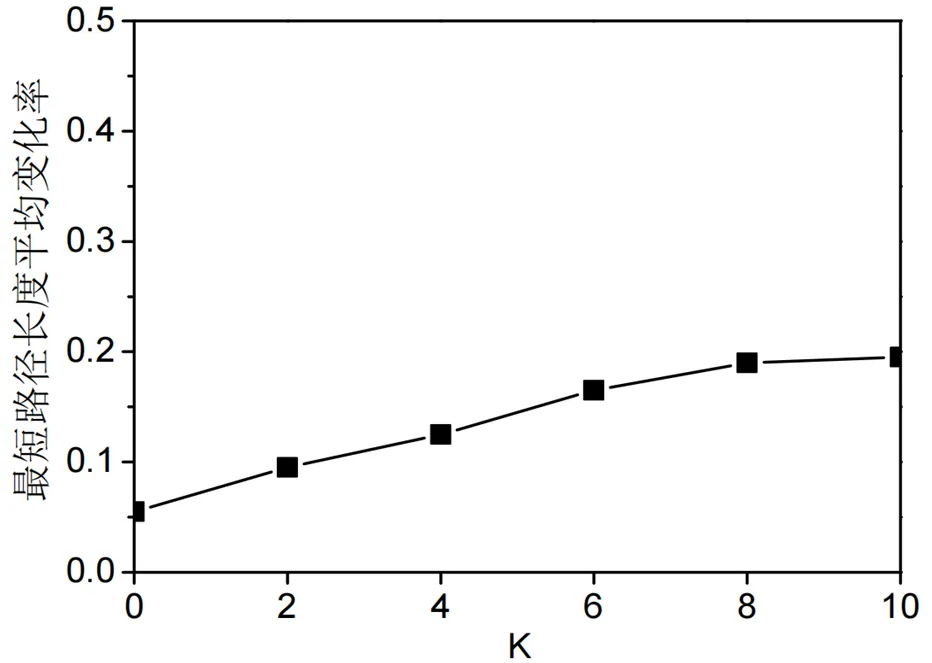
图6 保持20%目标对时最短路径长度随匿名程度的变化
在图6中,x轴为匿名程度k,y轴为最短路径长度平均变化率随匿名程度的变化。最短路径长度平均变化率是指匿名路径上所扰动边的权重修改量之和占原始边权重之和的百分比。将匿名扰动前后的矩阵进行比较,发现随着k值的增加,最短路径长度与扰动前近似相等,说明GEWP算法能够很好地保持原始图的数据信息。另外,H中所有敏感节点对的最短路径被精确保留。
从图6还可以看出,保持20%目标对时,即使大量目标对希望保持完全相同的最短路径和最短路径长度,扰动的最短路径长度仍然非常接近原始路径长度。除此之外,20%目标对的最短路径在扰动后保持不变。
4 结论
基于边缘集使用三个基本操作对原始加权社会网络进行修改,达到所需的k度匿名值,建立了一种保留社会网络中重要边缘的方法。该方法考虑边缘相关性并保留社会网络中重要边缘,保留原始网络图中某些节点对之间的最短路径和最短路径长度。实验证明,使用这种方法,可以明显改善数据的效用,减少匿名数据的信息损失。
[1] Ferri F, Grifoni P, Guzzo T. New forms of social and professional digital relationships: the case of Facebook[J]. Soc Netw Anal Min, 2011, 2(2): 121-137.
[2] Backstrom L, Dwork C, Kleinberg. Wherefore art thou r3579x? Anonymized social networks, hidden patterns, and structural steganography[J]. Communications of the ACM, 2011, 54(12): 133-141.
[3] Julian Salas, Vicenc Torra. Graphic sequences, distances and k-degree anonymity[J]. Discrete Applied Mathematics, 2015, 188(1): 25-31.
[4] Liu K, Terzi E. Towards identity anonymization on graphs[A]. Laks V. S. Lakshmanan, Raymond T. Ng, Dennis Shasha. Proceedings of the 2008 ACM SIGMOD international conference on Management of data[C]. New York, USA: ACM Press, 2008: 93–106.
[5] Casas Roma J, Herrera Joancomart, Jordi, Torra, Vicenç. k-Degree Anonymity And Edge Selection: Improving Data Utility In Large Networks[J]. Knowledge & Information Systems, 2017, 50(2): 1-28.
[6] Chester S, Kapron BM, Ramesh G, Srivastava G, Thomo A, Venkatesh S. Why Waldo befriended the dummy? k-anonymization of social networks with pseudo-nodes[J]. Soc Netw Anal Min, 2013, 3(3): 381-399.
[7] Bhattacharya M, Mani P. Preserving privacy in social network graph with k-anonymize degree sequence gener- ation[A]. IEEE: 2015 9th International Conference on Software, Knowledge, Information Management and Applications (SKIMA)[C]. Washington D. C., USA: IEEE Press, 2015: 1-7.
[8] Hartung S, Hoffmann C, Nichterlein A. Improved upper and lower bound heuristics for degree anonymization in social networks[A]. Joachim G, Jyrki K. International Symposium on Experimental Algorithms, Copenhagen, Jun 29-Jul 1, 2014[C]. Berlin, Heidelberg: Springer, 2014: 376-387.
[9] Li Y, Li Y, Yan Q, et al. Privacy leakage analysis in online social networks[J]. Computers & Security, 2015, 49(C): 239-254.
[10] Tsai Y C, Wang S L, Hong T P, et al. [K1, K2]–anony- mization of shortest paths[A]. Tao Y H, Chen L M, Lee C N. Proceedings of the 12th International Conference on Advances in Mobile Computing and Multimedia[C]. New York, USA: ACM Press, 2014: 317- 321.
[11] Tsai Y C, Wang S L, Hong T P, et al. Extending[K1, K2] -anonymization of shortest paths for social networks[M] //Jerry C W L, Ting I H, Tang T, Wang K. Multidisci- plinary social networks research. Berlin: Springer, 2015: 187-199.
[12] 张晓琳,何晓玉,张换香,等.PLRD-(k,m):保护链接关系的分布式k-度-m-标签匿名方法[J].计算机科学与探索, 2019,13(1):74-86.
Anonymity Algorithm for Weighted Social Networks with Sensitive Edge Weights
BI Hong-jing, LU Li-lei
(Department of Computer Science, Tangshan Normal University, Tangshan 063000, China)
Focusing on the privacy preserving of large data networks, a k-degree anonymous network was constructed. A greedy edge weighted perturbation (GEWP) algorithm for shortest path keeping was proposed for the utility of publishing data. It disturbed the weights of some edges to prevent the privacy disclosure problem and preserve the shortest path and length of the path between certain pairs of sensitive nodes in the original network. Simulation results matched theoretical analysis well.
weighted social network; sensitive edge weights; k-anonymity; privacy protection
TP309.2
A
1009-9115(2021)06-0041-05
10.3969/j.issn.1009-9115.2021.06.011
河北省自然科学基金(F2019105134),河北省教育厅科学技术研究项目(ZC2021030),唐山师范学院科研基金(2017C06)
2020-12-10
2021-10-09
毕红净(1983-),女,河北唐山人,硕士,讲师,研究方向为隐私保护、信息安全。
(责任编辑、校对:田敬军)

