Voronoi尾流规避下的风电场布局安全性研究

任建华，牛 旺，张宁可，王 键

(河北工程大学 机械与装备工程学院，河北 邯郸 056038)

0 引言

风电场是风力机组在其中运行捕获风能并产生电能的场所，风通过1台风电机后会因为风电机叶片的搅动而产生尾流，如果风力机之间的排布间隔过小，下游风电机将处于上游风电机的尾流之中，导致下游风电机的发电量减小，间隔过大则有盈余的风能不能被捕获利用[1]。

尾流效应的存在不仅影响能量产出的多少，同时也影响对输出电网的稳定性、安全性，过大或者过于频繁的电压波动势必会损害电网的运行器件[2]。对于风机机体而言，尾流降低了下游入流风的大小，间接影响了风电机的低电压穿行能力，在风况不理想的情况下，不仅降低了电能的品质而且增加了电网系统崩溃的严重故障率[3]。科学合理的风机布局，可以有效地保证风电场的稳定输出而不出现危险波动，具有60%以上宽容度。过于简单的布局不能获得稳定高产出，而过于复杂的布局则需要消耗较高的技术和维护成本。因此，需要合理的、程序化的布置机组并优化机组排布理论，以降低尾流影响为前提，同时达到降低布局技术难度、提高风电场能量产出和安全供电的的生产需求。

关于风电场布局优化理论的研究，近十年的研究可谓成果斐然。Sisbot等将多目标优化方法引入到风电场机组优化研究中[4]。David等利用精确梯度信息，展示了非线性数学的有效性，利用问题目标和约束的精确梯度信息求解连续变量的风场机组优化问题的数值规划[5]。Rabia等基于区域尺度和定点选择技术的风电场布局优化研究，通过面积旋转法来确定风电场形状的最佳尺寸，在此基础上，用定点选择的方法安置风机[6]。Harrison提出了1种新的混合整数线性规划公式，用于求解固定数量相同的风力发电机组的最优布局，使风电场发电量最大化[7]。Jaydeep等提出1种基于几何模式的风电场布局优化方法[8]。本文讨论多种类的布局方法，本着规避尾流影响的原则，着重研究几何布局法。

受上述研究的启发，本研究引入Voronoi图修正法，主要目的是利用几何规律规避尾流的影响，在风电场设计阶段即对布局方案进行优化。以WAsP为仿真计算软件平台，计算在同场内优化前后的尾流损失以及年净发电量变化结果；并以Voronoi图的特性为前提，结合人工智能、细分迭代计算等知识，深入探讨其发展前景和拓展应用实践。

1 优化理论

1.1 尾流衰减模型

由Jensen[9]开发的运动学尾流模型是最古老、应用最广泛的尾流模型之一。这个尾流衰减模型利用质量守恒定律计算上游尾流对下游风机的影响。Jensen尾流衰减模型如图1所示。

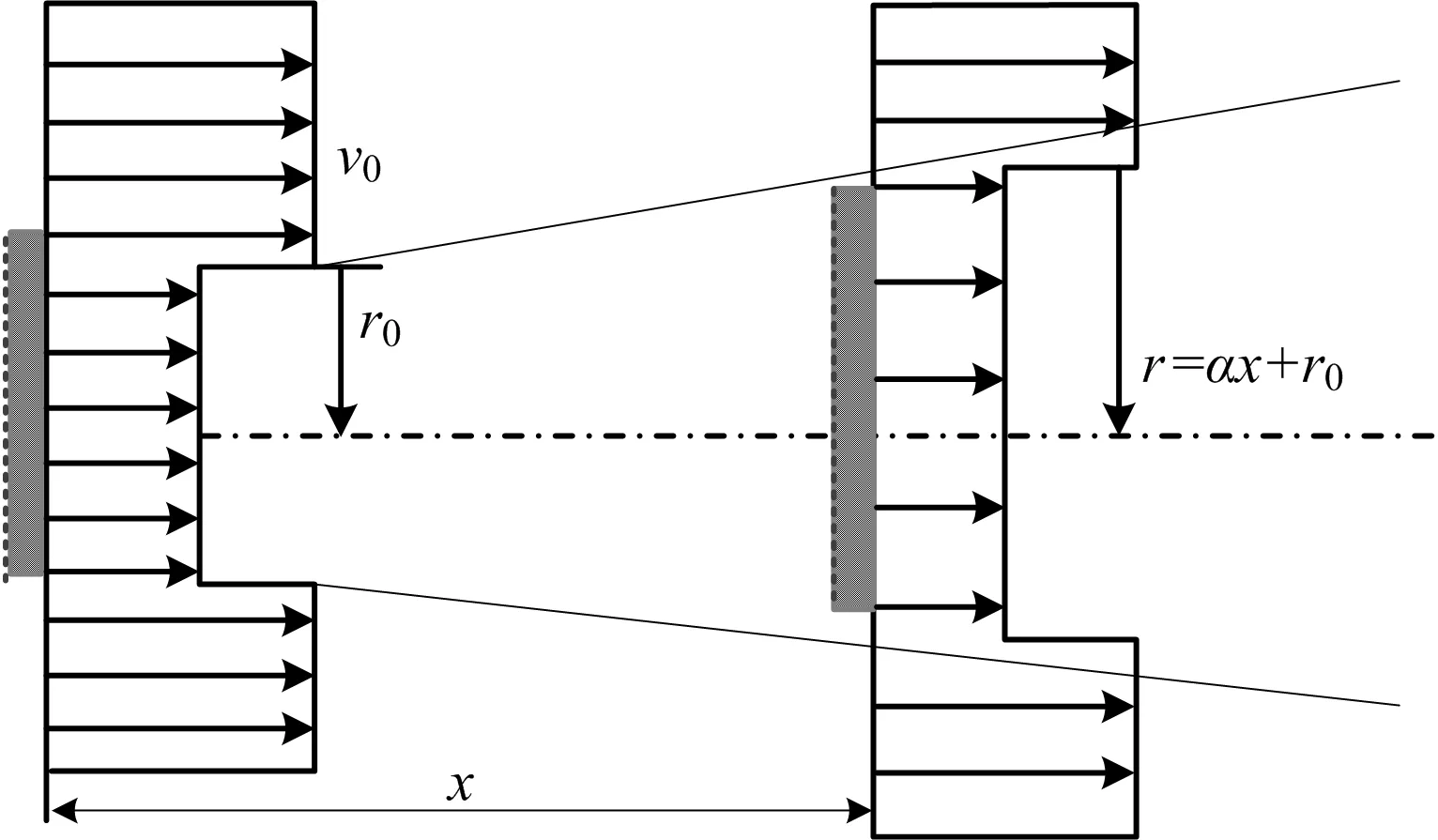
图1 Jensen尾流示意Fig.1 Schematic diagram of Jensen wake

改进的尾流衰减模型如公式(1):

(1)

式中：x为相邻风机间的距离，m；d为风力机直径，m；v0为风入流初速，m/s；r0是尾流初始半径，m；v为风电机下游实时速度，m/s；k由具体风电场实验确定的常数，β为一次模型修正系数，k、β、a为常数，a=1/3。有关改进的Jensen公式参考文献[10]。

本文在研究尾流计算模型时，提出指数倒数衰减修正式，如公式(2)：

(2)

1.2 Voronoi图

Voronoi图[11]又名泰森多边形，由美国气候学家A·H·Thiessen用来测量区域雨量[12]，得名于Georgy Voronoi，现多在无线网络优化等领域应用[13]，在建筑结构[14]和传染病疫情区域统计[15]上也有着广泛的应用，其是由2个相邻节点的垂直平分线连接形成的连续多边形构成。常见的生成方法有分治法、线扫描算法和Delaunay三角剖分算法，Delaunay三角形是最常用的生成方法。MATLAB中也有相对应的程序块。图2即为泰森多边形示意图。

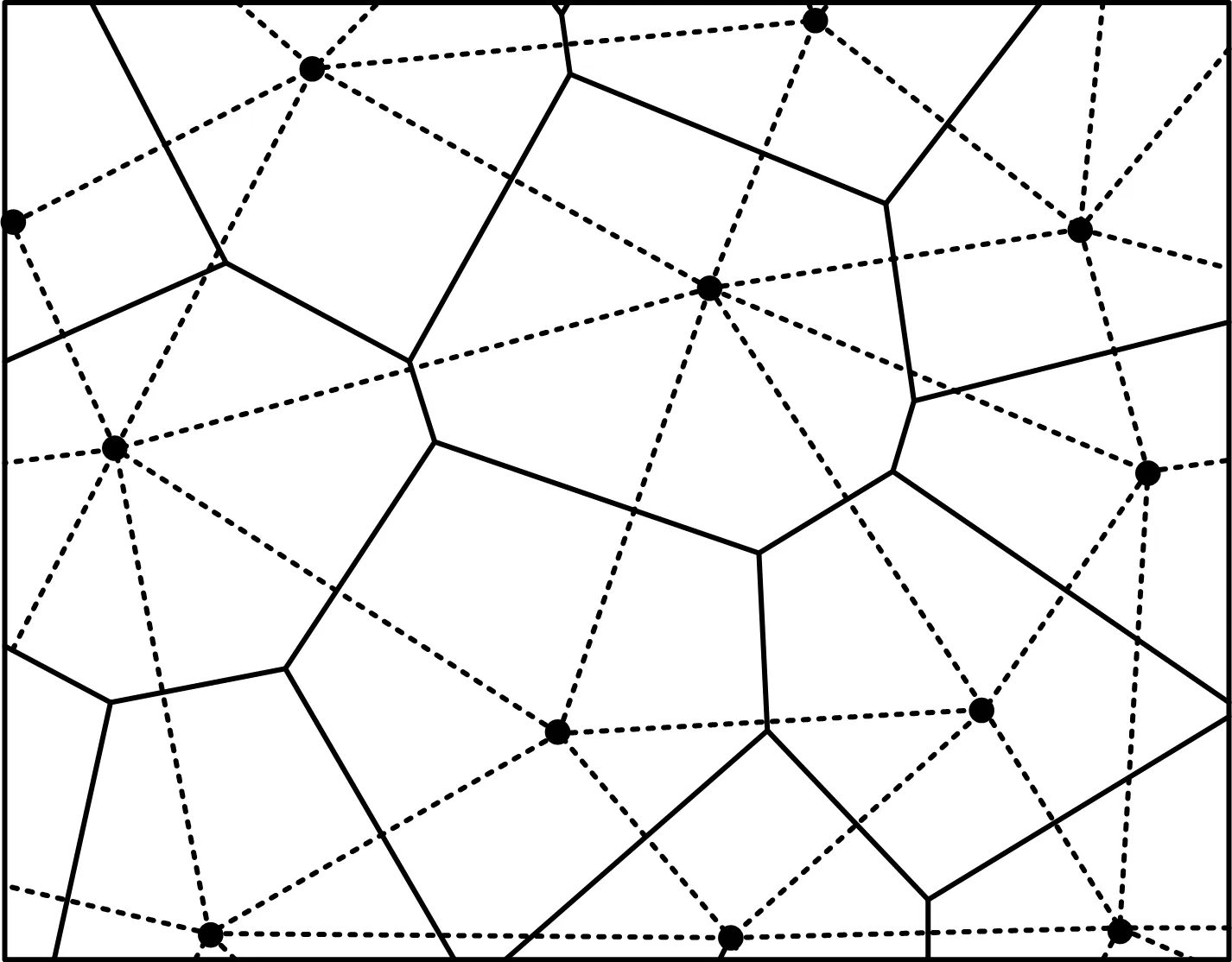
图2 Voronoi图Fig.2 Voronoi diagram

泰森多边形的基本特性是[16]：1)每个离散点只对应包裹在1个泰森多边形内；2)泰森多边形内的点到相应离散点的距离最近；3)位于边上的点到其2边的离散点的距离相等。

离散点的特性可以描述泰森多边形的性质；可用离散点的数据计算出泰森多边形区域的数据；相邻多边形对应相邻离散点；n边泰森多边形周围相邻n个离散点；在泰森多边形中的数据点距离该多边形的离散点最近。

泰森多边形最著名的应用是A·H·Thiessen的离散气象站测雨量以及约翰斯诺霍乱图，分别在文献[12]和文献[17]有详细的说明。结合上述文献以及泰森多边形的特性可以得出：泰森多边形的中心离散点可以辐射作用其多边形上的所有顶点以及其多边形范围，反映到风点场布局，即可阐述为被选中的离散点风机构成的泰森多边形内的风机间尾流有互相影响，将互相影响的风机偏移出对应多边形影响范围即可达到规避尾流效应的目的，进而降低风电场发电的湍流波动。

2 风况设置

在实际施工中的风况主要有风速、风向2大参数，但是通常情况下是无序随机的，无法用数学表达式表示。近十年的文献研究中，有关学者在统计整理实地测量风况数据中发现，以年为单位的风况变化是符合统计学规律的[18]。本文主要集中研究风场的优化理论，故在风况的设置上将采取基于实际数据库或理论研究的假设法。

2.1 风速计算

威布尔分布函数[19]是一种常用的用以描述长期风速变化规律的数学表达式，其表达式为公式(3)～(4)：

(3)

(4)

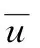
2.2 风向

风向的表示通常使用玫瑰测定图，用以表示长时间的风向变化规律。本文以参考文献[20-21]的风数据标准为筛选依据，以WAsP官方科研数据为对象，得年平均风速为8.00 m/s，其玫瑰测定图如图3所示。

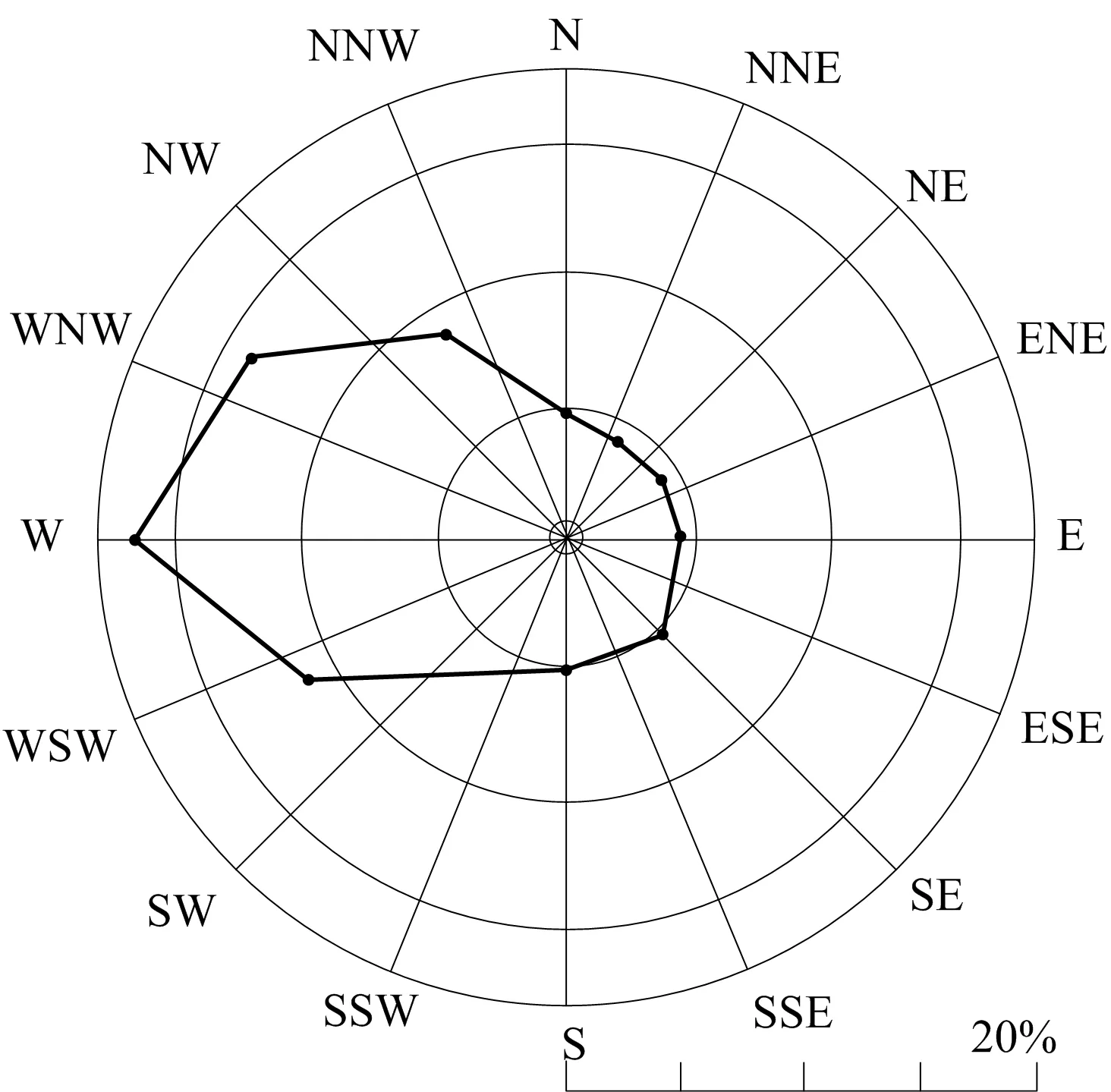
图3 风况玫瑰图Fig.3 Wind rose diagram

3 模拟计算边界条件设定

本文计算用风电机参数：在已经确定平均风速的前提下，采用WAsP内置1 MW风力机，参数如表1所示。

表1 风力机参数Table 1 Parameters of wind turbine

理论上，风力机的特征输出功率(单位kW)计算可表示为公式(5)：

(5)

式中：CP为风电机的功率系数，通常取值0.4；ρ为风密度，通常取值为1.2；R为风轮半径，m。将参数带入到式(5)中，得公式(6)：

P(u)=0.3u3

(6)

普遍的，当风速小于4 m/s时，风力不足以推动叶片进行发电，故此时功率为零。

以每台风力机的平均功率作为最后比较的依据，用P(u)ave表示为公式(7)：

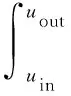
(7)

在WAsP中导入矢量图.map文件作为风电场布置的地形影响如图4，其横向长度为5 000 m，纵向长度5 000 m。尾流衰减因子由经验设定为0.75。

图4 风场矢量Fig.4 Vector diagram of wind field

4 风电场布局Voronoi几何法

遵照Voronoi图的构建方式和性质，即可得出Voronoi法的特定布局理论。

首先选择无需变化位置的特征风机，这些风机的特征是：1)最上游风机位置不变，因为入流风最大，且无尾流效应的干扰；2)下游风机不对在上游任何一台风机的正后方，相邻上下游距离在9个叶片直径之外除外；3)横纵向相邻风机遵循近距离双向交错的原则。

在选择特征风机后，相邻点连成Delaunay三角网，在这基础上按照文献[16]提供的方法绘制出Voronoi图。下面将通过最常用的计算布局法和最新的圆形几何布局法做详细的说明。

4.1 计算布局优化

计算布局即在数学的科学计算理论基础上，通过复杂的场景计算获得设计布局，通常情况下借助计算机开发软件系统，在软件系统中搭建模拟场景，进而获得各个机位的准确布置点。在此类软件中，以WAsP和Windfarm为商业软件代表，已经在科学研究和具体风电场项目中得到广泛的应用。

在科研人员研究中，某一研究的对象通常不是系统的计算工程，而是针对某1种布局算法进行的；另一种情况则是只针对布局的上游算法，如在确定风场布局前的尾流算法，通过计算尾流效应的分布、大小，结合诸如粗糙度、风速、风向等要素，在模拟软件中以最有效的方式计算出最终布局，文献[20]即为在可信数据上进行的实验研究，最后得出风电场布局，图5所示为文献[20]的最优方案布局。

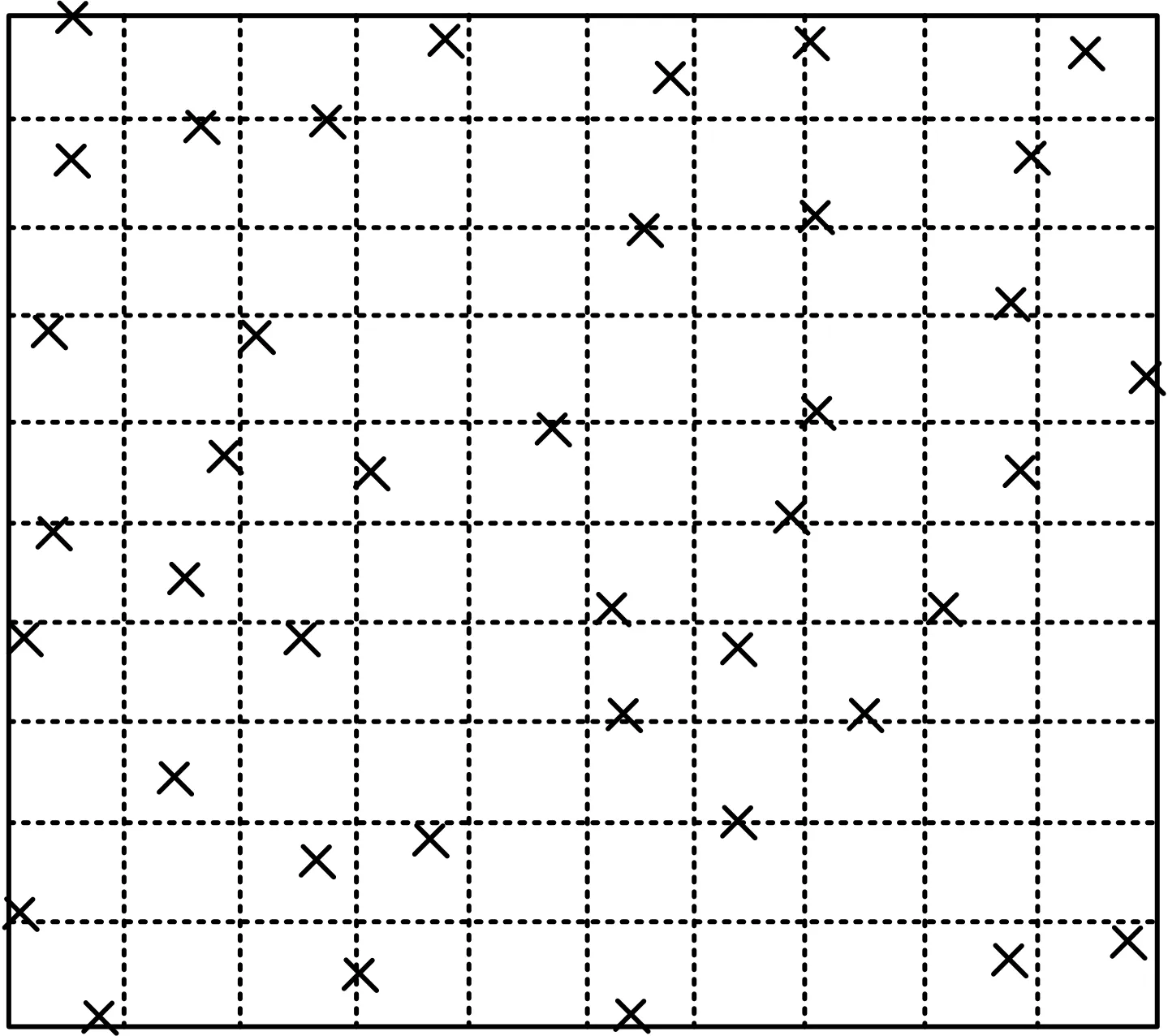
图5 计算布局Fig.5 Calculation layout

Voronoi法优化后得图6～8，图8即为优化后的最终布局。

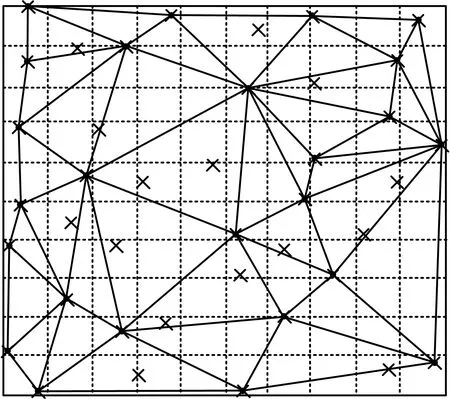
图6 Delaunay三角网Fig.6 Delaunay triangle network

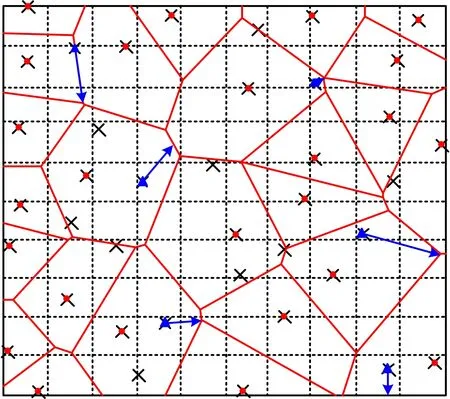
图7 生成Voronoi图Fig.7 Generated Voronoi diagram

图8 计算布局优化后Fig.8 Calculation layout after optimization

4.2 圆形几何布局法优化

几何布局法是1种新方法，也是本文研究的核心要点，此方法是由Jaydeep Patel[8]等在2018年ICAE会议上提出，其区别于Mosetti等[22]在1994年提出的基于网格的风机排布方式，规避了离散网格在空间解算上单一的局限性。几何布局方法的优点包括：

1)几何规律强，可视化属性强，类比机械设计当中的作图法，如凸轮的作图法、四杆机构的运动分析方法等，无论工作人员有无专业知识背景，只需要按照几何作图法即可得出符合条件的基础风场布局设计。其特定的几何规律下的布局在向其他研究人员、管理人员、投资方解析时简单易懂，无需非常深奥的专业知识的灌输即可理解。

2)程序化思维路线，几何布局以几何图形为基础，而几何图形可以被很好地计算机软件化，软件的底层设计为节点式，在封装好的节点程序块后，构建从顶到底的流程(类似机械设计当中的Top-Down设计)，1次构建可任意替换其中任意节点，可参照MATLAB的simulink模块和Houdini软件的运行模式。

3)与人工智能的互联性以及强大的交互性，人工智能目前最主要的应用实践，其最后处理的目标都是图像或者图像序列，例如车辆牌照识别系统，天眼系统人脸识别，谷歌AlphaGo，英伟达针对TensorFlow设计Tensorcore，英特尔针对图像噪点设计的开源AIDenoiser算法，Adobe软件的AI动态抠像，无损AI放大软件Topaz Video Enhance AI等，这些都是人工智能在图像领域的实地生产力转化实例。本文风电场布局研究就是将三维的空间转换为二维的平面布局，可将本文提出的Voronoi图算法与人工智能结合，利用AI训练实现智能识别绘制，风电场的布局方法即可大大简化。

图9为Jaydeep Patel等在其研究中提出的布局最优解，其布局的规律明显比上述2种更加规律。

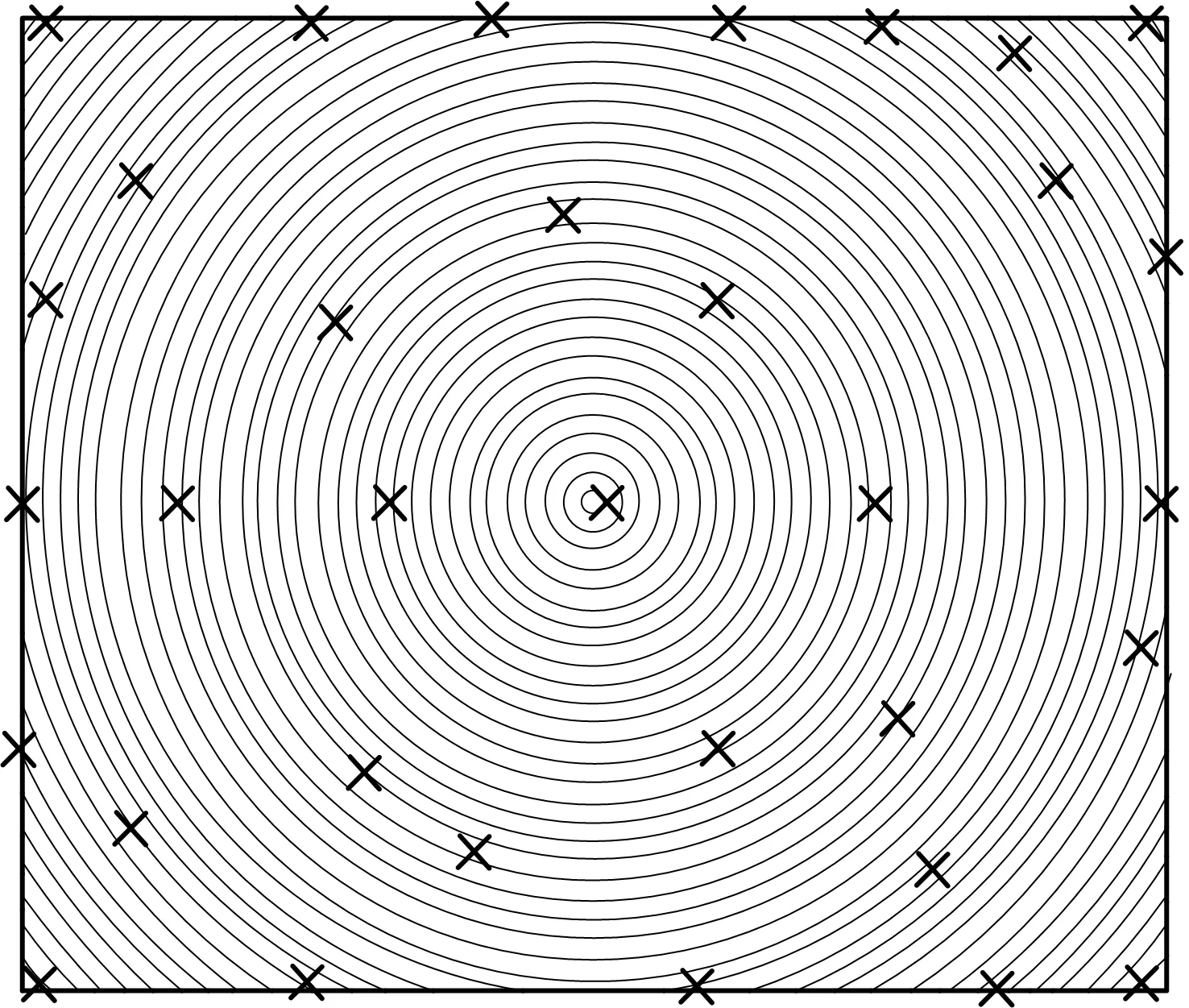
图9 圆形几何布局Fig.9 Circular geometric layout

Voronoi图修正：绘制方法也同上，不再赘述。得图10～12，图12即为Voronoi几何优化后的最终布局。

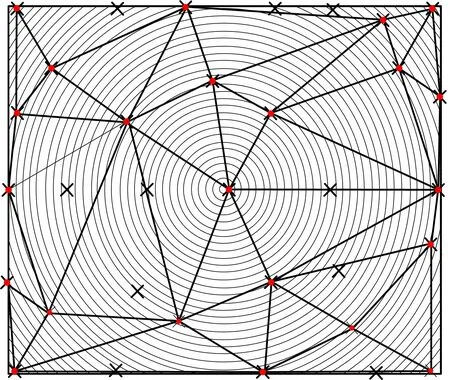
图10 Delaunay三角网2Fig.10 Delaunay triangle network 2

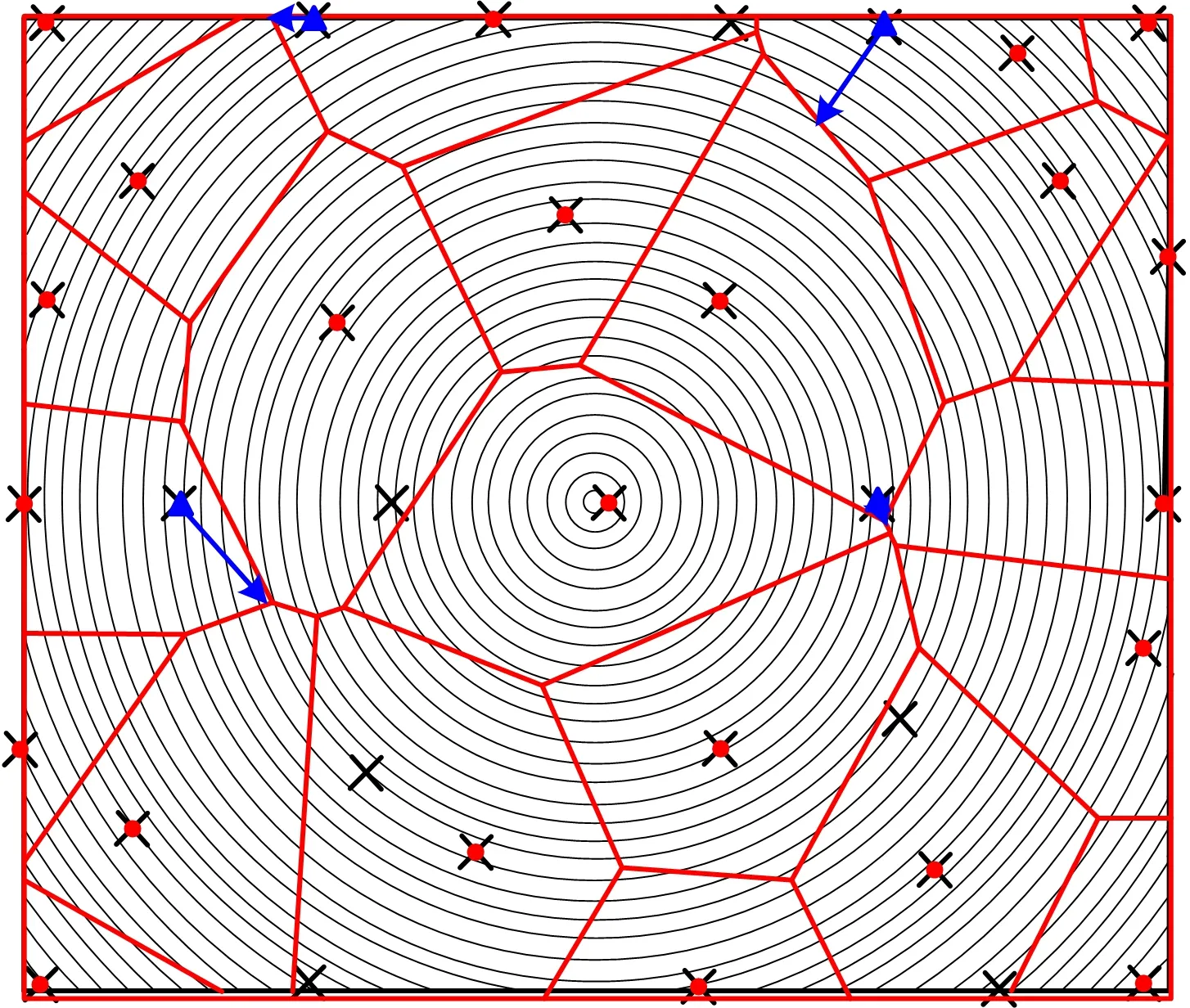
图11 生成Voronoi图2Fig.11 Generated Voronoi diagram 2

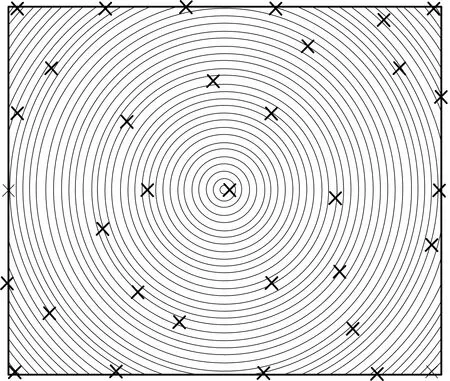
图12 圆形几何布局优化后Fig.12 Circular geometric layout after optimization

5 WAsP计算结果以及分析

本文分别对一般的2种布局方法所得到的风电场机组布局进行了Voronoi优化，分别为计算布局和圆形几何布局。在WAsP中搭建计算布局和圆形几何布局优化前后共4组风场，计算得出结果：

1)计算布局在优化后的总尾流损失降低9.46%，单个风机最大降幅达62.50%，年发电量(单位：GWh)增加4.26%。

2)圆形几何布局在优化后的总尾流损失降低6.25%，单个风机最大降幅达59.26%，年发电量(单位：GWh)增加4.18%。两者尾流损失在各个风机的数值上呈现更加平均化分布，尾流波动降低。

计算证明了在Voronoi的几何规则下进行的优化布局，是合理可行的，通过几何法则规避尾流的影响，能显著降低尾流的产生和波动，使得风场向电网输出更加平滑，进而提高电网系统的运行安全性[23]和电网小信号稳定[24]，同时对提高机组低电压穿越能力有较好的帮助。对比图5和图8、图9和图12，可以发现，经优化后的布局更加均匀，进而能捕获更多的风能量，在加上尾流损失降低，所以在此双重影响下年发电量得以大幅增加。

6 结论

1)Voronoi几何优化法很好地规避了尾流影响，进而降低了尾流损失，并且提高了风量利用率和输出稳定性，是1种全新的优化布局方法，该方法综合了强规律性、规范性、程序化、前瞻性等优点，值得继续深入研究。

2)在仿真中，单个风机的尾流损失不仅有大幅度降低，有些下游风机却增加了尾流损失，其中计算布局一些下游风机尾流增加1.19%～80.64%，圆形几何分布尾流增加在1.1%～34.37%。分析其原因：①仿真实验时，为了尽可能接近真实风况，引入了较大粗糙度的地形，影响了风的分布；②仿真所规划的Voronoi图是一次细分的，注重考虑尾流影响最显著的位置，其对下游风机的考量不够充分；③本文将Voronoi图首次应用到风电场布局优化中，主要针对地形较为平坦的陆上风电场布局或者是部分海上风电布局进行的，是基于二维尾流影响的优化方法。对于地形起伏较大的山区的风力发电机布置应用在理论上的普适性不强。

3)在此引入计算机图形学中的细分采样迭代概念，即可以进行多次特征取样，在一次布图后的新特征采样再次细分多边形，多次迭代后的泰森多边形将越来越小，相交叉领域也逐步细化，这样可以通过三角定位得出精确的风机位偏移坐标。