不同物候阶段木芙蓉叶功能性状特征
许跃坤,王 勇,王丽华,王文鑫,唐淑琴
(1.四川农业大学 林学院,四川成都 611100;2.阿坝师范学院,四川汶川 623002)
在植物生长发育过程中,由于资源的有限性及植物自身的生长、繁殖及防御等功能之间的竞争关系,植物对现有资源的利用策略会因资源可获得性的改变而发生变化。植物功能性状作为植物进化过程中适应外界环境的结果,是植物生存和适应环境的重要属性[1]。在植物各器官中,叶功能性状对气候变化敏感,不仅能反映植物对环境的高度适应能力,还能反映植物在复杂生境下的自我调控能力[2-3]。植物叶功能性状包括形态和生理性状,两者在适应环境的过程中相辅相成。植物在受到环境变化带来的压力时,会通过调节叶片结构与生理特征来响应,例如,植物在干旱环境下会通过减少比叶面积以减少水分的蒸发[4-6]。叶功能性状与植物的生长对策和资源利用策略的关系最密切,可直接影响植物的基本行为和功能[7],以植物叶片为研究对象,更能反映植物对环境变化的响应机制。
异速生长是指生物体某两个性状的相对生长速率不相同的现象,是由物种遗传所决定的固有特性,通过异速生长关系可系统地阐明植物个体大小和植物性状之间的内在关系[8-9]。叶片作为植物进行光合作用的主要场所,叶面积的大小直接影响植物对光的截取和碳的获取;叶柄是植物叶的重要支撑结构和水分、养分的输导通道,叶柄的支撑作用会随叶片大小的增加而增加[10]。叶片和叶柄的异速生长关系是植物功能生态学研究领域的热点。祝介东等[11]对不同生物气候带内植物的叶大小和叶柄间的生长关系进行研究,发现不同功能型和不同气候带的植物叶片干重、叶面积和叶体积与叶柄干重均存在显著的异速生长关系;李金明等[12]研究重庆地区常见的6种复叶树种的叶片与叶柄和叶脉的生长关系,发现叶片与叶柄、叶片与叶脉均呈显著的异速生长关系。比叶面积是描述植物叶片结构性状、植物光合特性和其他生理特性的重要参数,在一定程度上能反映叶片截获光的能力,其大小主要受自身因素和外界因素的影响[10,13-15]。比叶面积高的植物,叶面积普遍较高[16]。叶干物质含量是植物功能性状的另一个重要指标,能反映植物获取资源的能力,随着叶干物质含量的增加,叶内水分向叶片表面扩散的距离或阻力增大,更有利于植物内部保持水分[17]。比叶面积和叶干物质含量作为能反映植物适应环境能力的关键性指标,研究两者之间的异速生长关系可进一步揭示植物叶片对资源条件变化的响应。
木芙蓉(Hibiscus mutabilis)别名大芙蓉或拒霜花,为锦葵科(Malvaceae)木槿属落叶灌木或小乔木,原产地为中国,广泛分布于湖南、云南和四川等地。木芙蓉花色艳丽、花期较长,具有较高的观赏价值而被广泛应用于园林中[18]。目前,有关木芙蓉叶功能性状及异速生长模型的研究还未见报道。本研究以木芙蓉为研究对象,研究不同物候阶段(花芽期、始花期、盛花期和末花期)叶功能性状间的相关性,建立叶柄鲜重与叶片鲜重、叶干物质含量与比叶面积的异速生长方程比较各方程的拟合效果,期望找出木芙蓉在不同物候阶段叶功能性状组合及资源分配的特点,为深入了解木芙蓉的生态适应性、提高经营管理水平提供科学依据。
1 材料与方法
1.1 试验地概况
试验地位于四川省汶川县水磨镇阿坝师范学院校园内(103°25'E,30°56'N),海拔920 m,属山地亚热带湿润季风气候,年均降水量1 281.5 mm,年均气温13.9 ℃,年温差较小,年均无霜期260 天;土壤类型主要为山地黄棕壤。
1.2 物候期观测
2020年7月— 2020年10月下旬,在校园西北区域,避开高大建筑物及树木,选取树龄一致(10年生)、生长状况良好的20株木芙蓉并标号;在每株的东、西、南、北4 个方向各选4 根枝条作为观测对象并标记,7天观测1次。树体上出现花芽至花朵开放少于10%为花芽期(2020年7月19日— 8月16日);树体上10%左右花朵开放为始花期(2020年8月17日—8月30日);树体上60%左右花朵开放为盛花期(2020年8月31日—2020年10月11日);树体上90%左右花朵凋谢为末花期(2020年10月12日—10月25日)。
1.3 样品采集与指标测定
从每株植株的东、西、南、北4 个方向各选择完全伸展、成熟无病害且完整的叶片3 片和完全开放的花朵3个,用于相关指标的测定;每14天取样1次。
测定叶片性状时,用清水洗去叶片表面灰尘等杂物,擦干水分后采用叶面积仪(山东方科仪器有限公司YMJ-A)测定叶面积(LA);采用WinRHIZO根系分析系统扫描花朵,测定花投影面积(FPA);采用电子天平(精度为0.000 1 g)测量叶片鲜重(LFW)和叶柄鲜重(PFW),采用游标卡尺(精确至0.01 mm)测量叶柄长度(PL)和叶柄直径(PD)。将样品放入105 ℃烘箱杀青30 min[19],之后在80 ℃下烘48 h 至恒重,采用电子天平测量叶干重(LDW)和单个花重(SFW)。所有数据均测量3 次,取平均值。比叶面积(SLA,cm2∕g)、叶干物质含量(LDMC,g∕g)计算公式[20]如下:

1.4 数据处理
对PL、PD、LA、LDMC、SLA、SFW 和FPA 等数据进行正态性检验(S-W 法),将不符合正态分布的数据进行对数转换,使其符合正态分布,利用Levene’s test 检验方差齐性,再进行单因素方差分析。采用标准主轴回归(SMA)计算异速生长方程的斜率,根据Pitman 的方法计算斜率的置信区间[13]。采用SPSS 17.0 和R 2.0 软件的SMATR 包进行所有分析,采用Origin 2019作图。
异速生长关系式为Y=β·Xα,为使数据符合正态分布,对数据进行对数转换,关系式转换为logY=logβ+ αlogX。式中,Y为某种生物学特征或功能;β为标准化常数;X为个体大小;α为异速生长指数,α=1为等速关系,α ≠1为异速关系。比较斜率α之间及其与1 的显著性,若斜率α 间无显著差异,给出共同斜率,并检验各物候期间沿共同主轴偏移距离的差异性。
2 结果与分析
2.1 不同物候阶段叶片性状间的关系
在花芽期,PL与LFW 呈显著正相关(P<0.05),与PD、PFW 均呈极显著正相关(P<0.01);PD 与LFW 呈显著正相关(P<0.05),与LA、PFW 均呈极显著正相关(P<0.01);LDMC 与LFW、PFW 均呈极显著负相关(P<0.01);SLA 与LA 呈显著正相关(P<0.05),与LFW 呈极显著负相关(P<0.01);LA与LFW 和PFW、LFW 与PFW 均呈极显著正相关(P<0.01)(表1)。

表1 不同物候阶段不同功能性状间的Pearson相关性Tab.1 Pearson correlations among different functional traits at different phenological stages
在始花期,PL 与PD、SFW、LFW 和PFW 均呈极显著正相关(P<0.01),与LDMC 呈显著负相关(P<0.05),与SLA 呈极显著负相关(P<0.01);PD 与LFW、PFW 均呈极显著正相关(P<0.01),与SLA 呈极显著负相关(P<0.01);LDMC 与LFW、PFW 均呈极显著负相关(P<0.01);SLA 与LA 呈极显著正相关(P<0.01),与FPA、LFW 和PFW 均呈极显著负相关(P<0.01);LA 与FPA 呈显著负相关(P<0.05);LFW与PFW呈极显著正相关(P<0.01)。
在盛花期,PL 与SFW 呈极显著正相关(P<0.01);PD与SFW呈显著正相关(P<0.05),与LDMC呈极显著负相关(P<0.01);LDMC 与LA 呈显著正相关(P<0.05),与SLA、LFW 均呈极显著负相关(P<0.01);SLA 与LA 呈显著正相关(P<0.05);LFW与PFW呈显著负相关(P<0.05)。
在末花期,LFW 与PFW 呈极显著正相关(P<0.01),LDMC 与SLA 和LFW、LA 与PFW 均呈极显著负相关(P<0.01)。
2.2 不同物候阶段叶柄鲜重与叶片鲜重的异速生长关系
LFW 和PFW 从花芽期至末花期均呈先上升后下降趋势,LFW 在始花期最大(2.170 g),PFW 在盛花期最大(0.507 g)(表2)。不同物候阶段PFW 的变异系数均大于LFW,LFW、PFW 变异系数分别为17.23%~34.29%、35.29%~57.05%。
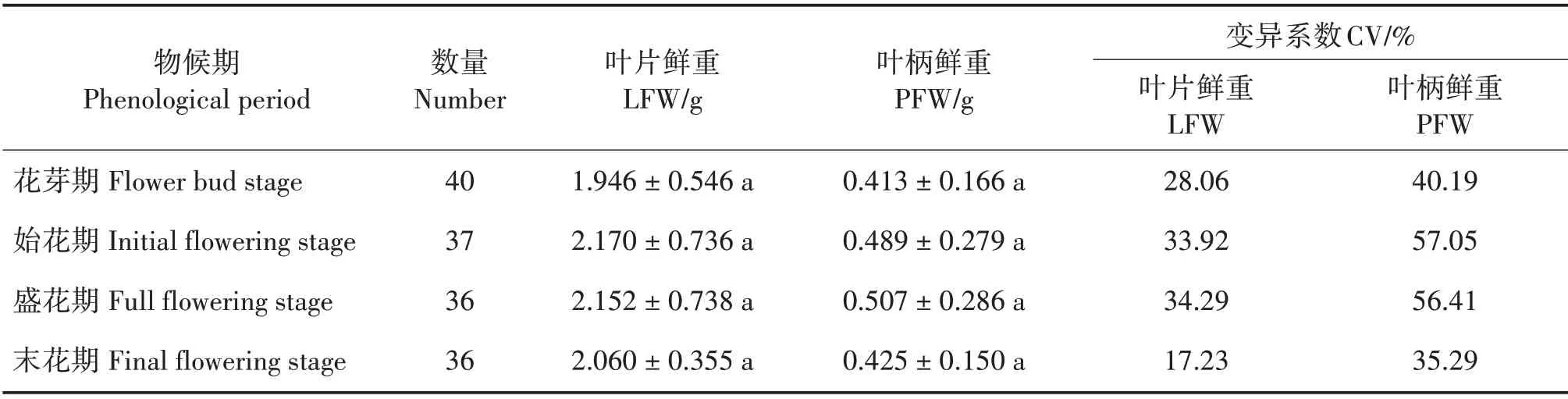
表2 不同物候阶段叶片鲜重和叶柄鲜重变化Tab.2 Changes of LFW and PFW at different phenological stages
从花芽期至末花期,SMA 斜率分别为0.585(95%置信区间为0.603~0.895)、0.390(95%置信区间为0.408~0.631)、-0.065(95%置信区间为-0.877~ -0.444)、0.057(95%置 信 区间为0.239 ~ 0.468)(表3,图1)。花芽期、始花期和末花期的斜率与1有显著差异,盛花期的斜率与-1 有显著差异,均为异速生长关系。多重比较表明,花芽期的斜率显著或极显著大于始花期和末花期(P<0.05,P<0.01),始花期和盛花期的斜率显著大于末花期(P<0.05),即花芽期叶片鲜重的增长比始花期和末花期快,始花期叶片鲜重的增长也比末花期快,盛花期叶片鲜重的增长比末花期慢。花芽期和始花期与盛花期的斜率差异不显著,花芽期与盛花期的共同斜率是0.563(95%置信区间为0.594~0.836,P=0.400),始花期与盛花期的共同斜率为0.136(95%置信区间为0.449 ~ 0.649,P= 0.307)。对截距进行分析,发现这几个物候阶段在y轴截距没有显著差异。
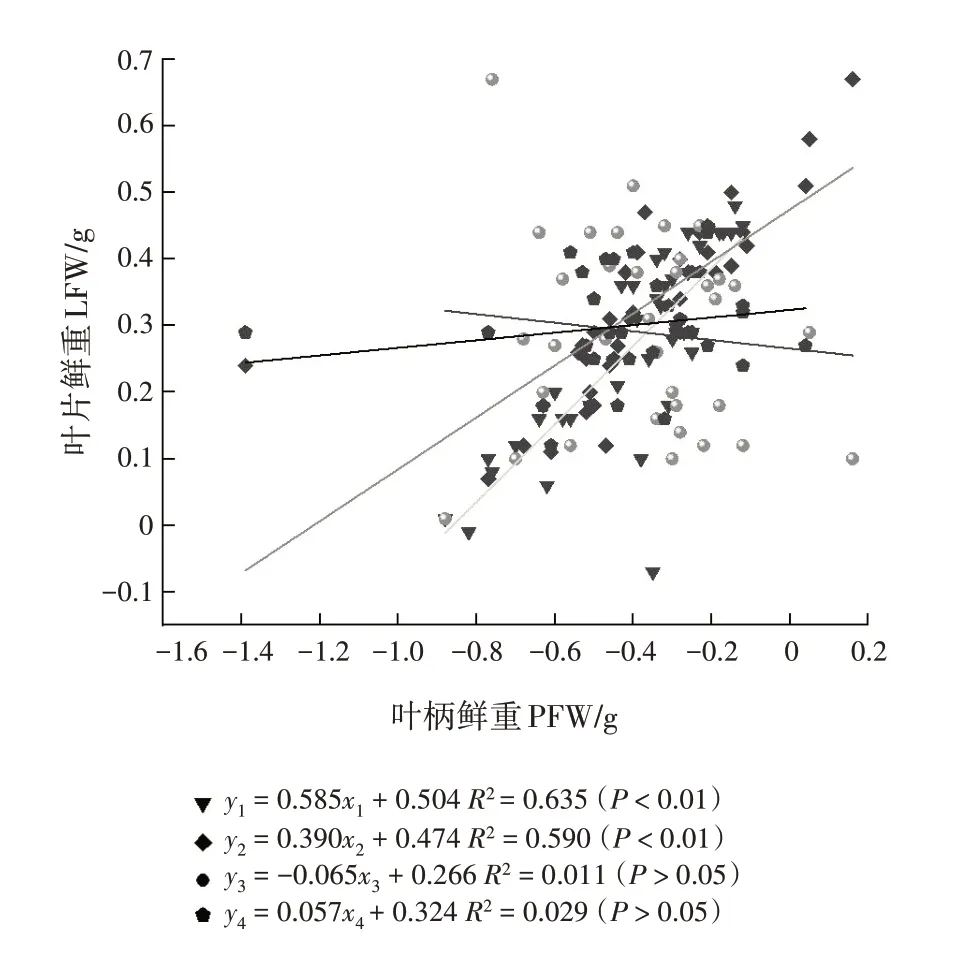
图1 不同物候阶段叶片鲜重与叶柄鲜重的相关关系Fig.1 Correlations between LFW and PFW at different phenological stages
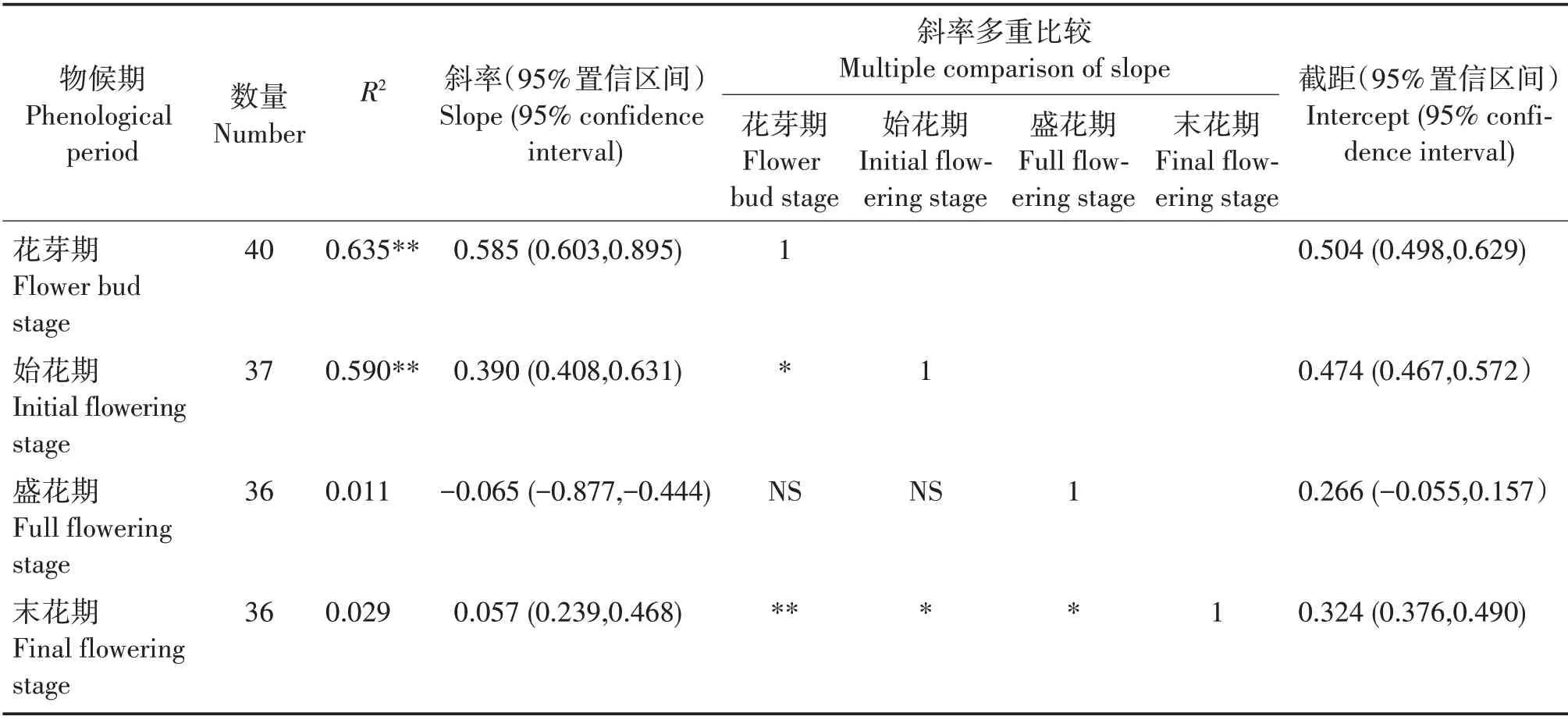
表3 叶片鲜重与叶柄鲜重的SMA回归参数与多重比较分析Tab.3 SMA regression parameters of LFW and PFW and multiple comparison analysis
2.3 不同物候阶段比叶面积和叶干物质含量的异速生长关系
从花芽期至末花期,SMA 斜率分别为-0.002(95%置信区间为-0.767 ~ -0.429)、-0.010(95%置信区间为-0.544 ~ -0.473)、-0.002(95%置信区间为-0.700 ~ -0.527)和-0.001(95% 置信区间为-0.876 ~ -0.777)(表4,图2)。花芽期至末花期的斜率与-1 均有显著差异,均为异速生长关系。多重比较表明,花芽期的斜率显著大于始花期(P<0.05),极显著大于末花期(P<0.01);始花期的斜率极显著大于盛花期和末花期(P<0.01)。花芽期和盛花期的斜率差异不显著且共同斜率为-0.002(95%置信区间为0.594 ~ 0.836,P= 0.324),盛花期与末花期的斜率差异不显著且共同斜率为-0.006(95%置信区间为-0.033~-0.472,P=0.116)。对截距进行分析,发现这些物候阶段在y轴截距没有显著差异。
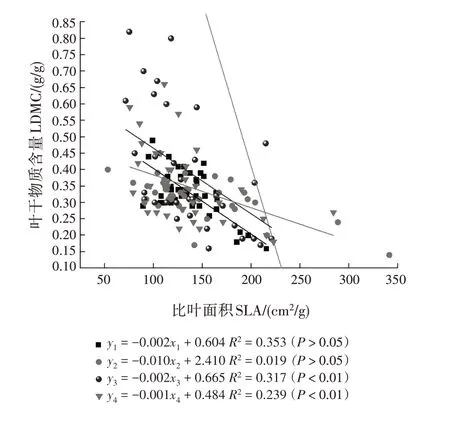
图2 不同物候阶段叶干物质与比叶面积的相关关系Fig.2 Correlations between LDMC and SLA at different phenological stages
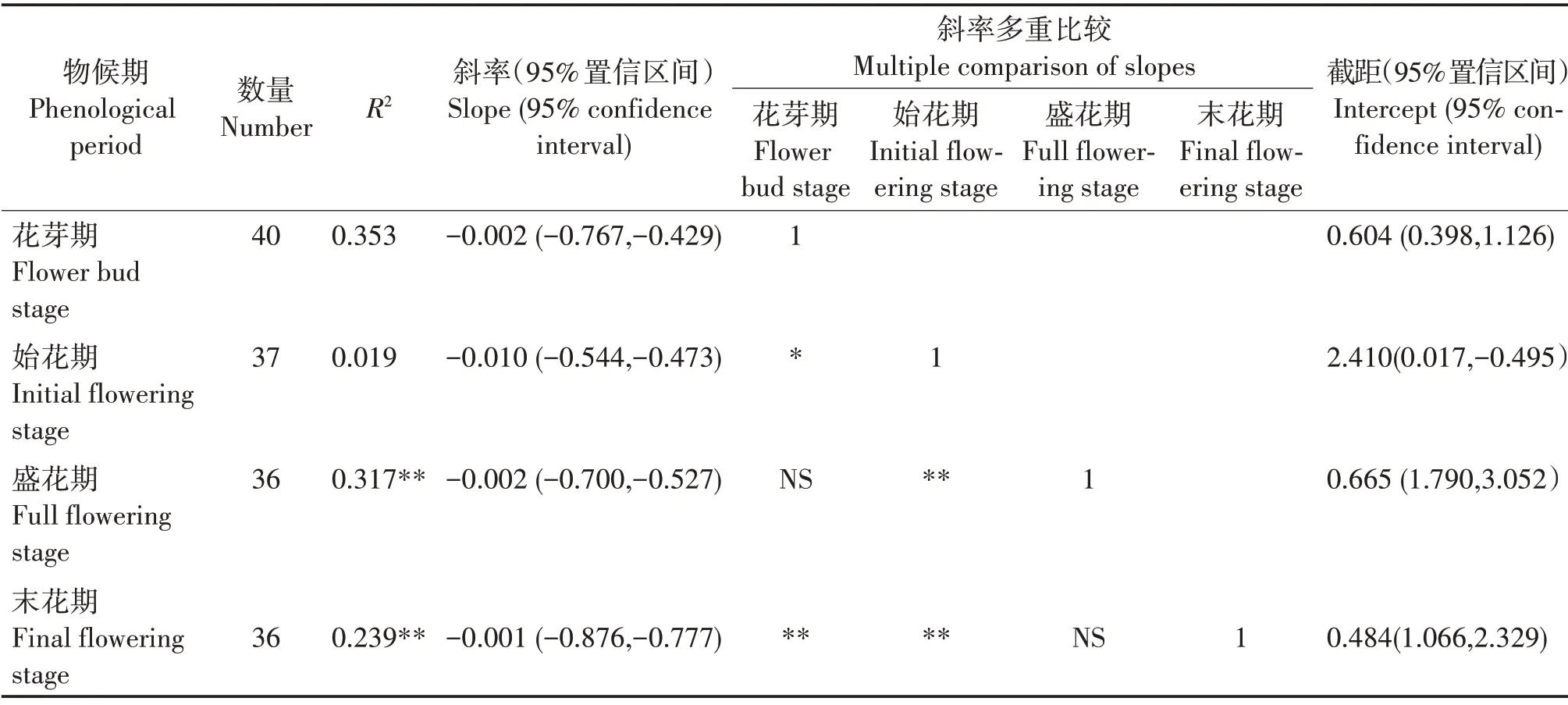
表4 叶干物质含量与比叶面积的SMA回归参数与多重比较分析Tab.4 SMA regression parameters of SLA and LDMC of H.mutabilis and multiple comparison analysis
3 讨论与结论
3.1 叶片与叶柄的相关性
植物会通过长期的内部功能调整,最终形成一系列功能性状组合,以适应环境的变化[21]。物种在生长发育和适应环境的过程中,植物功能性状间的相关关系会发生改变[22]。本研究中,随着物候期的变化,叶功能性状组合也发生改变。在花芽期,PL随LFW、PD 和PFW 的增加而增加,PD 随LFW、LA和PFW 的增加而增加;在始花期,PL 随PD、SFW、LFW 和PFW 的增加而增加,PD 随LFW、PFW 的增加而增加;在盛花期,PL、PD 均随SFW 的增加而增加;到了末花期,LA 随PFW 的增加而减小,PL 和PD与其他性状均不存在显著相关性。原因可能是随着花期的到来,木芙蓉会消耗大量的同化物,为保证足够的同化物,植物可能会通过增加叶面积以获取更多的碳和光能。叶面积增大后要遭受更大的拉拽力,叶柄也要具有更强的支撑力[11,23]。到盛花期和末花期,由于叶片老化,叶片光合色素含量比前期减少,光合能力减弱,使叶片有机物积累减少,呼吸消耗增强,同化速率减缓[24]。
SLA 反映植物获取资源的能力,LDMC 反映植物对养分的保有能力[25]。本研究中,盛花期和末花期的SLA 与LDMC 均呈极显著负相关,与前人研究结果一致[26-28]。花芽期和盛花期的SLA 与LA 均呈显著正相关,说明木芙蓉在花芽期和盛花期叶片构建的资源随着叶面积增加而增加,与王雪艳等[29]的研究结果一致。在花芽期,LDMC 随LFW 和PFW 增加而减小;在始花期,LDMC 随PL 和SLA 增加而减小;在盛花期和末花期,LDMC 随SLA 和LFW 增加而减小。原因可能是木芙蓉处于开花期,叶片光合作用同化的产物更多地被分配给繁殖构件(花数量、花质量)和支撑结构(叶柄、叶脉)来共同完成开花[14],使木芙蓉叶片本身的资源保存量大大减少。
3.2 不同物候阶段叶的资源利用策略
本研究中,木芙蓉叶片鲜重与叶柄鲜重从花芽期至末花期均呈异速生长关系,研究结果与杨冬梅等[4]的研究结果一致。其原因可用“管道模型理论”进行解释,即理论上,植物输导组织的横截面积与其所在叶片的叶面积是等比例关系,但叶柄除了具有传导水分和养分等功能和作为叶片的支撑结构外,还需承受整个叶的静态重力和外界的动态拉力等,这些因素使得在叶水平上的叶柄和叶片之间存在异速生长关系[30]。当以叶鲜重表示叶大小时,木芙蓉为增加叶大小所付出的代价有可能比其获得的收益更大。对大叶物种,适当地延长枝条、茎和叶柄长度,可有效减少叶片间的遮荫,有利于提高叶的光拦截效率[31-32]。
植物叶干物质含量与比叶面积呈显著负相关的异速生长关系[33-34]。本研究结果与前人研究结果一致,原因可能与木芙蓉在生长过程中有机物积累和消耗之间的权衡有关[16,35]。以往研究结果表明,植物的SLA 随叶龄增加而增大,在同一物种中,SLA小的成熟叶(或幼龄叶)比SLA 大的老龄叶更具活力和抵抗力[36]。因此,随着物候的更迭,因叶片衰老、温度下降等原因,叶片的含水量降低,透光性变差,光合能力降低,使LDMC含量增加、SLA降低。
本研究仅对木芙蓉叶性状间的相关性及生长关系进行了研究,不同物候阶段木芙蓉枝叶之间的生长关系可作为后续研究。

