水下航行器空化噪声偏度和峰度分析
张 俊,王明洲,胡友峰
(中国船舶集团公司第七〇五研究所,陕西西安 710075)
0 引 言
空化是一种由于液流局部压力低于相应温度下的饱和蒸汽压力导致的包含空泡初生、长大、收缩和溃灭的过程,并在局部空间内产生高温、高压、微射流以及对外辐射噪声的流体动力学现象[1]。
当水下航行器航行速度和外部流体压力满足一定的条件时,在航行器表面不连续处容易产生空化现象。一般来说航行体速度越高、流体压力越小、航行姿态越不稳定越容易出现空化现象。
充分空化情况下,在航行体表面会产生并附着大量气泡。一方面,采用专用空化器产生的大量气泡极大地减小了航行体的水下航行阻力,可以有效地提高航行速度,例如基于超空泡原理设计的水下航行器最高速度可以达到200 kn(1 kn=1 842 m·s-1)。另一方面大量空泡湮灭过程中因体积剧烈收缩而产生的空化噪声具有强度大、频谱宽的特点,从而大幅度降低了水下目标检测的信噪比,严重影响了水下航行器的目标探测性能。对空化噪声的特性进行研究,有利于水下航行器声呐系统的科学设计,对提高声呐检测性能具有重要的价值。
目前,对空化及空化噪声的研究已经十分充分,从1917年Rayleigh建立不可压缩流中球形空泡的运动方程和证明空泡溃灭时将对外辐射声脉冲以来[2],许多学者在理论、实验、数值计算方面不断完善和发展了相关理论以及研究方法[1,3]。基于Rayleigh方程,Fitzpatrick等[4]在1956年建立了空化噪声数学模型,采用傅里叶变换分析方法得到空泡溃灭时间和空化噪声频率的关系,证明空化噪声谱密度函数正比于频率的四次方。同时期,国外开始从实验方面对空化及空化噪声进行研究。随后伴随着计算机技术的发展,开展了对空化过程的数值模拟研究,极大地提升了对空化噪声的研究手段。在90年代末和本世纪初,国内上海交通大学、西北工业大学等单位也对空化噪声进行大量的研究工作。文献[5-8]中,戚定满、武延祥、范飞等分别建立了单空泡、多空泡和区域群体空化噪声的数学模型,对噪声谱特性进行了计算研究;文献[9-11]通过实验途径测量和研究了空化噪声的相应特性;文献[12-13]则基于计算机仿真软件对空化过程和空化噪声进行建模,研究了不同条件下空化噪声的特点。
当水下航行器表面空化充分发展时,水下航行器接收的信号中包含了大量高强度的空化噪声,为了保证水下航行器对目标的有效检测,必须尽量减少空化噪声对真正目标信号的干扰。有别于对水下航行器空化噪声的仿真建模和能量特性研究,本文基于试验中测量到的数据,对空化噪声的偏度和峰度进行了计算分析,比较了不同条件下空化噪声的偏度和峰度特性差异,较之常规能量特性研究和频率特性研究,本文的研究为水下航行器空化噪声的特性研究提供了不同的思路。研究结果能够用于空化噪声背景下目标辐射噪声与空化噪声的分离及识别。
1 水下航行器空化噪声
空泡从生成到湮灭的过程实质上是空泡体积膨胀和压缩的过程。在湮灭阶段,空泡膨胀到最大半径后破裂产生一个尖峰压力并伴随声波辐射。这个过程十分迅速,噪声声压一开始就接近阶跃式快速上升并在湮灭结束时刻达到最大声压值。空泡湮灭时的辐射噪声是空化噪声的主要成分,可以认为空化噪声就是空泡湮灭过程中产生的噪声。
因此对于接收点来说,单个空泡产生或者空泡群集中产生的空化噪声是一个非常尖锐的脉冲信号,这个脉冲的持续时间极短,包含非常丰富的频率信息。当空化噪声脉冲达到最大值后,其声压值并不立即下降为零,而是呈振荡形式续存一定的时间。所以接收点接收的空化噪声是以空泡湮灭产生的声压脉冲为起始的振动衰减信号,可以表示为[8]


Pm是空泡噪声脉冲的最大声压幅度,当空泡收缩到其最小半径时声压达到的最大值。Pm与空泡最大半径Rmax和最小半径Rmin相关,关系为[7]
其次,消费者在购物时除了关注商品品牌与品质,还应了解商品价格构成,清楚分析自己可以获得的收益,慎重选择商家和产品。根据模型的分析结果可知,消费者在不同标价方式下作出的不同策略选择会使自己获得不同的收益,在不包税价下选择购买单件或使订单总额小于2,000元,以及在包税价下选择购买套装,都会使自己获得更多的收益。问卷调查结果虽显示,过半数的调查对象都会做出与模型结论完全相符或部分相符的选择,但仍有一部分调查对象无法做出最利于自己的购物策略选择。绝大多数调查对象并不知道或不关心自身收益的差别,这就给了线上零售商从关税方面赚取多余利润的机会。

式中:0P为液体压力;r为接收点与空泡中心的距离。根据Rayleigh对空化现象的理论研究结果,空泡从开始破裂到完全湮灭的时间可表示为[2]

式中:ρ为流体密度。而空泡湮灭时产生的空化脉冲的时长T0与空泡湮灭时间TC成比例关系[7]

其中,K'为常数,且有:

可见K与空泡最小半径与最大半径的比例有关。在持续时间上,空化噪声可以分为开始的声压脉冲长度T0和后续振荡时间。在时域波形上,声压脉冲持续时间为后续振荡衰减信号周期的1/4。所以空化噪声的角频率为

对于水下航行器而言,空化噪声的产生与其头部流体线型、航行深度、航行速度和航行姿态密切相关。一般而言,航行深度浅(对应水压力小)、速度高以及航行姿态不稳定均是空化产生的有利条件。图1和图2为水下航行器在浅水高速航行条件下测得的空化噪声时域波形。从图1波形可以看出,空化充分发展条件下空化噪声由众多声压脉冲组成。从图2单脉冲空化噪声波形可以看出,空化噪声开始有一个比较明显的冲击脉冲,能量快速上升随后立即下降,但是并不立刻消失而是持续振荡一段时间后逐步消失,振荡周期约为冲击脉冲存在时间的4倍,这与理论分析相符合。

图1 空化噪声波形Fig.1 Waveform of cavitation noise
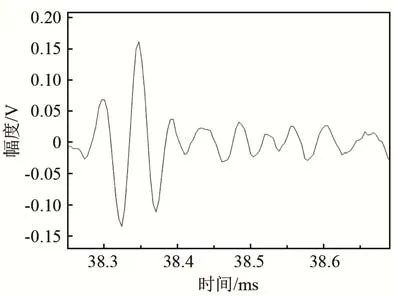
图2 单脉冲空化噪声波形Fig.2 Waveform of the single-pulse cavitation noise
2 空化噪声偏度与峰度分析
2.1 偏度与峰度


偏度和峰度表征的是对高斯分布的偏离程度。偏度是分布不对称性的度量,当偏度为正时,说明随机变量概率密度分布曲线的面积集中分布在中心的左侧,当偏度为负时则说明分布在中心的右侧。峰度则衡量了随机变量的概率分布与高斯分布之间的差异,是随机变量的概率密度分布曲线相对于高斯概率密度分布曲线尖锐或者平坦程度的度量。直观看来,如果峰度大于3,分布曲线的形状比较尖,比高斯分布曲线陡峭,反之则曲线较高斯分布曲线平坦。
2.2 空化噪声偏度与峰度分析
2.2.1 单脉冲空化噪声分析
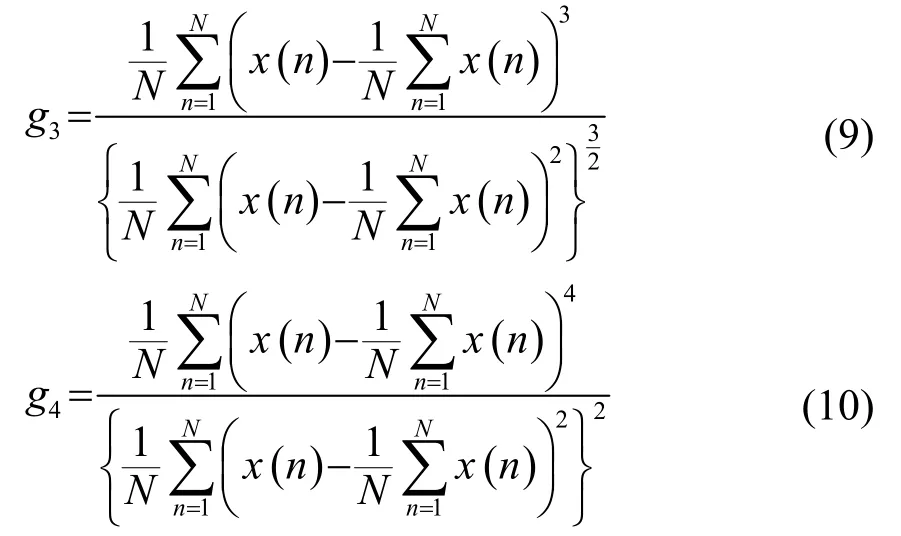
本文将只具有单个明显声压脉冲的空化噪声定义为单脉冲空化噪声。根据前文中空化噪声的理论分析,声压脉冲的生成是单个空化气泡湮灭或者气泡群集体湮灭时的必然过程,声压脉冲是空化噪声的单元组成和明显特点。所以本文首先对单脉冲空化噪声进行偏度和峰度的分析计算。
图3为待分析的单脉冲空化噪声波形,数据长度为0.8 ms。对该空化噪声的概率密度分布、方差、偏度和峰度进行计算,并与图4所示的理想高斯噪声(理论均值为0,方差为1)进行比较。二者的方差、偏度和峰度结果见表1,空化噪声和高斯噪声概率归一化分布图如图5所示。

图3 用于分析的单脉冲空化噪声波形Fig.3 Waveform of the single-pulse cavitation noise to be analyzed
由表1中的计算结果可见,空化噪声方差为0,远小于高斯噪声的方差0.948,在图5中的噪声概率密度分布曲线上表现为在0左右分布非常集中。空化噪声的偏度为0.856,说明其概率分布曲线并不是中心对称而是主要分布在中心的左侧。空化噪声的峰度为9.637,明显大于高斯噪声的峰度,说明空化噪声不服从高斯分布,其概率分布曲线有着更为尖锐的峰,这是空化噪声较为明显的一个统计特性。

图4 高斯噪声波形Fig.4 Waveform of Gaussian noise

表1 空化噪声和高斯噪声统计特征对比Table 1 Comparison of statistical characteristics of cavitation noise and Gaussian noise

图5 空化噪声和高斯噪声概率分布曲线Fig.5 Probability distribution curve of cavitation noise and Gaussian noise
2.2.2 试验数据分析
选取4组水下航行器实测噪声进行偏度和峰度计算,各组噪声长度为45 ms。为了便于对比,选取了不同空化发展程度下的噪声数据进行分析。其中噪声1和噪声2为无空化条件下测得数据,噪声3和噪声4为空化充分发展条件下测得数据。图6与图7为各组噪声的时域波形,表2为各组噪声的峰度和偏度计算结果。
从表2中结果可见,在无空化条件下和空化充分发展条件下对应噪声的偏度和峰度值差异较大。噪声1和噪声2是水下航行器航行在深水处,航行器表面无空化现象发生时所测噪声,其主要成分是水中环境噪声和自身平台噪声。可见该条件下两组噪声的偏度和偏度值一致性较好,偏度均接近 0,峰度均约为 3,可知两组噪声幅值的概率分布接近高斯分布。

图6 无空化时实测噪声Fig.6 The measured noise without cavitation

图7 空化充分发展时实测噪声Fig.7 The measured noise of fully developed cavitation

表2 实测噪声偏度和峰度Table 2 Skewness and kurtosis of measured noise
噪声3和噪声4为水下航行器航行在浅水高速情况下所测噪声,这时空化发展充分,从时域噪声波形上可以明显观察到众多声压脉冲,两者偏度和峰度值基本一致且与噪声1和噪声2相差较大。噪声3和噪声4的偏度为正值,与噪声1和噪声2偏度相差一个数量级,可见其概率密度分布曲线不是中心对称而是偏向中心的左侧。噪声3和噪声4峰值相比噪声1和噪声2峰值亦明显增大,相差5倍左右,说明噪声3和噪声4幅值的分布更为集中。由此可见,当空化现象充分发展时,空化噪声表现出明显的非高斯特性。
水下航行器进行目标被动检测过程中,需要逐帧实时地对通道接收信号进行处理和检测。对各通道接收信号的偏度和峰度的时间分布进行计算,可以为检测过程中噪声的识别和分离提供一定的参考。本文对以上四组实测噪声的偏度和峰度进行逐帧计算和分析,设定滑动窗长度为2 ms,滑动步长为0.5 ms,滑动窗对数据进行滑动,计算窗内2 ms长度数据的偏度和峰度。画出偏度和峰度曲线如图8~11。从各数据偏度和峰度曲线可以看出,没有空化噪声时,偏度和峰度时间曲线相对平坦,其数值接近高斯分布偏度和峰度数值;当空化充分发展时,由于存在大气泡湮灭或者气泡群的不连续湮灭,从而产生了众多幅值较大的不均匀分布的空化脉冲信号。噪声偏度和峰度在尖峰脉冲处明显增大,整体偏度和峰度曲线起伏明显。

图8 噪声1偏度和峰度时间分布曲线Fig.8 Skewness and kurtosis time distribution curve of noise 1


图9 噪声2偏度和峰度时间分布曲线Fig.9 Skewness and kurtosis time distribution curve of noise 2
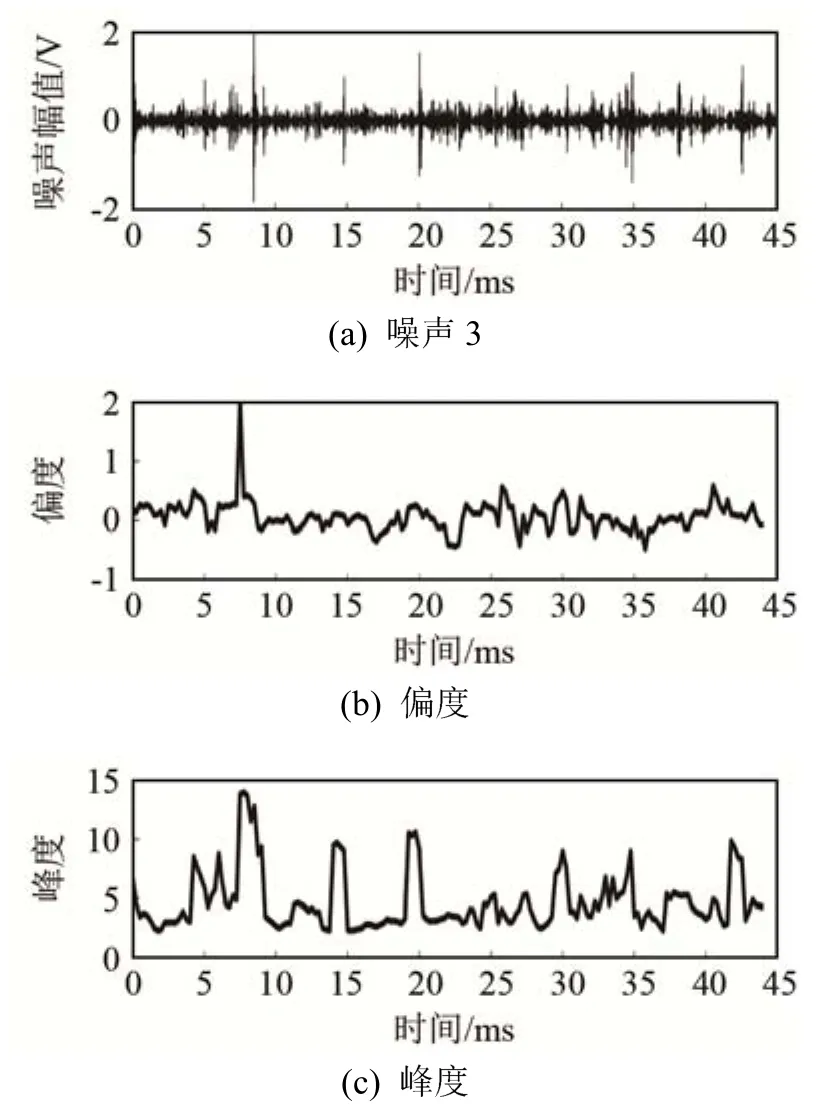
图10 噪声3偏度和峰度时间分布曲线Fig.10 Skewness and kurtosis time distribution curve of noise 3

图11 噪声4偏度和峰度时间分布曲线Fig.11 Skewness and kurtosis time distribution curve of noise 4
3 结 论
根据以上计算和分析的结果,水下航行器空化噪声具有明显的非高斯特性,与高斯噪声或者海洋环境噪声相比有明显差异。在空化充分发展时,空化噪声波形具有幅度分布不均匀、声压脉冲明显的特点,其偏度和峰度数值明显高于高斯分布的偏度值和峰度值,且在时间分布上与空化脉冲相对应,偏度和峰度时间分布曲线起伏明显。在后续工作中,基于本文的研究结果,可结合水下航行器目标辐射噪声的偏度和峰度分析,对目标辐射噪声和空化噪声的分离的具体方法开展研究,以提高水下航行器在空化背景下的被动目标检测能力。

