双平行线阵的水下二维DOA估计算法

姚 泽，张 歆,2

（1.西北工业大学航海学院，陕西西安 710072；2.鹏城实验室，广东深圳 518000）

关键字：双平行线阵；传播算子算法；二维波达方向估计；自主式水下航行器

0 引 言

自主水下航行器（Autonomous Underwater Vehicles,AUV）在进行水下搜救、环境监测、数据采集等领域的需求越来越多，其工作也越来越复杂[1]。单个AUV所实现的工作是有限的，而集群AUV协同系统具有空间、时间、功能的分布性，能扩展单AUV的功能，但是同时也提高了工作的复杂度[2]。在集群AUV进行水下作业时，协同作业成为了其完成复杂任务的重要环节，而多个AUV水下协同工作时，彼此之间的位置信息就十分重要。对多个AUV目标的二维波达方向（Direction of Arrival,DOA）估计是AUV水下协同作业必须要解决的问题。目前水下AUV一般采用通信、定位一体化方法进行位置信息的确定，利用通信信号时延进行距离估计，再进一步对其进行二维DOA估计，通常使用长、短基线对水下目标进行估计。在小型AUV上，基阵阵列长度等受载体体积和换能器尺寸的限制；小尺寸、低功耗的工作环境条件对于水下DOA估计提出了更高的要求。实际应用时，所采用的算法和尺寸需要结合上述条件进行选择，还要保证一定的估计精度。

DOA估计应用于雷达、生物、声呐等领域[3-4]，其中，二维DOA估计得到了广泛关注[5-7]。要获得高精度的DOA估计需要合适的阵型和DOA估计算法。在二维DOA估计中，一般采用直线阵、L型阵、平面阵或矢量传感器，并且按照阵元排布也可以分为均匀阵、非均匀阵。近年来，非均匀阵中的互质阵[8-9]得到了关注，其通过互质关系对阵列进行虚拟重构的特性使得阵列测向自由度得到提升，但其重构造成计算量加大，导致整体处理过程的复杂度提高。在常用平面阵列结构中，由等距线阵构成的衍生阵近年来由于结构简单、易于实施、估计效果良好等受到人们的广泛重视，平行阵就是其中的一种。

二维多重信号分类算法（Multiple Signal Classification,MUSIC）[10]和二维旋转不变子空间算法（Estimation of Signal Parameters via Rotational Invariance Techniques,ESPRIT）[11]是DOA估计的经典算法，并且都属于子空间算法。子空间算法的核心就是对接收信号的协方差矩阵进行特征值分解或奇异值分解，从而获得信号子空间或者噪声子空间，进行二维谱峰搜索，这类计算较为复杂，往往涉及到庞大的计算量。文献[12]中指出，子空间算法在大规模多输入多输出（Multiple-Input Multiple-Output,MIMO）系统中，这种劣势尤为明显，这在多源信号估计的条件下同样存在。文献[13]中提出了最大似然法，根据最大似然准则，对输出数据进行时空二维处理来获得估计结果。之后又提出了子空间算法的改进算法，但算法计算复杂度较高。复杂度过高不利于算法在处理能力较弱、或对功耗有限制的场景应用，AUV作为低功耗水下平台，其分配在定位方面的处理资源有限，无法进行高复杂度的定位处理计算。二维传播算子（Propagator Method,PM）算法不需要互相关矩阵的特征值分解和接收数据的奇异值分解就可以快速得到噪声子空间[14]，计算复杂度大大降低，阵列信号的处理性能也得到了极大地提高，更多地应用于低功耗系统中。近些年来PM算法的应用越来越多，基于PM算法的二维DOA估计方法得到了广泛关注。

本文设计适合了AUV平台的水下二维DOA估计算法，选取了双平行线阵。双平行线阵由两组平行线阵组成，两者相互垂直构成阵列模型，具有平移不变性，有较好的阵列分辨率，易于构造协方差矩阵。且本文采用的PM算法可以通过协方差矩阵快速得到噪声子空间，不需要对协方差矩阵的特征分解计算。输出DOA估计结果时，避免了二维谱峰搜索，可以得到自动配对的二维DOA估计结果，具有较好的二维DOA估计性能，减少了计算量，计算方法复杂度相对较低。这种复杂度较低的算法，对于整个系统的功耗控制较好，利用通信信号与声学定位一体化方法，将高频通信信号作为AUV水下信号源进行DOA定位处理，高频信号的短波长特性，使得小尺寸阵列在水下DOA估计中得以使用，整体估计方法满足了AUV水下DOA估计平台对于小尺寸、低功耗的要求，并且有较好的估计精度。

1 算法模型

1.1 双平行线阵阵列模型

阵列几何结构如图1所示，在平行线阵基础上，进行垂直方向的扩展，得到双平行线阵。在x-y平面中，有Lx1，Lx2，Ly1，Ly2四条均匀线阵，其中Lx1和Ly1由相邻阵元间距为d的N+1个阵元组成；Lx2和Ly2由阵元间距为d的N个阵元组成；Lx1和Lx2平行于x轴放置，彼此平行间距为d，构成沿x轴方向的平行线阵，Ly1和Ly2平行于y轴放置，彼此平行间距为d，构成沿y方向的平行线阵。

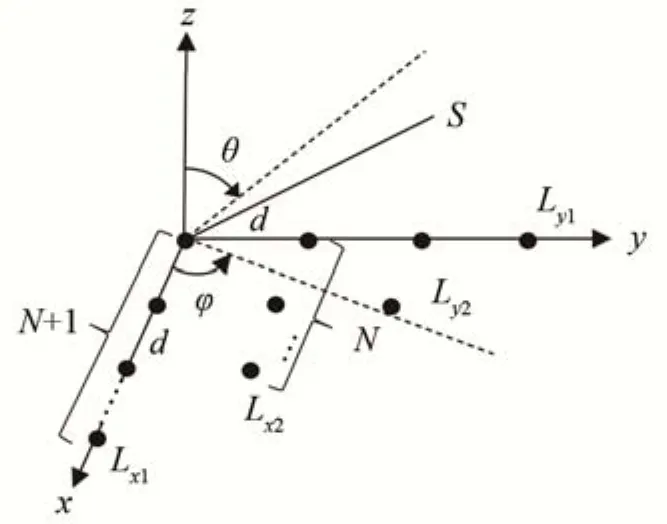
图1 双平行线阵阵列结构图Fig.1 Configuration of double parallel linear array

式中：λ是信号波长，Lx2的导向矢量矩阵Ax2是Ax1的前N行，定义：

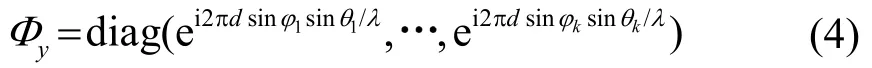
其中，diag（·）表示对角矩阵。同理可得与y轴平行的平行线阵Ly1和Ly2的阵列输出信号yy1和yy2，表示为

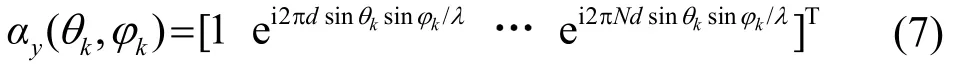
Ly2的导向矢量矩阵Ay2是Ay1的前N行，定义：

两种平行线阵的信号形式相似，本文以与x轴平行的平行线阵为主进行二维DOA算法介绍，同理可得与y轴平行的线阵结果。

1.2 二维DOA估计算法

1.2.1 阵列输出重构

将与x轴平行的平行线阵的阵列输出合并表示为

其中，Ax为与x轴平行的平行线阵的矢量导向矩阵

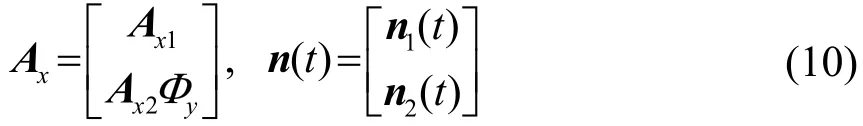
1.2.2 基于PM算法的二维DOA估计

将上一步重构得到的x轴方向平行线阵的矢量导向矩阵Ax进行分块：

其中：右上角表示矩阵的行列数，且A1是非奇异矩阵，这样分解得到的A1、A2是具有线性关系的两个子矩阵，这种关系可以表示为

这里的PH是一个行列数为K×（2N+1-K）的矩阵，定义为传播算子矩阵，之后的算法围绕这里的PH矩阵进行。考虑接收数据的协方差矩阵为

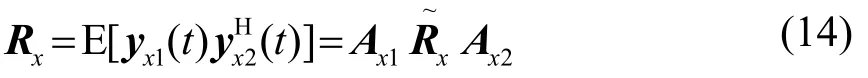
由于实际应用中，快拍数为有限值，所以无法精确得到式（14）中的Rx理论值，一般使用离散形式的计算进行近似，即：

同样，对此协方差矩阵进行分块处理：

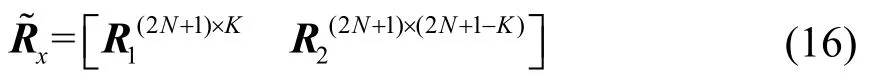
理论上，这种分块处理得到的R1、R2也是具有线性关系的两个子矩阵，在无噪声情况下可表示为

这里的P就是传播算子矩阵。但是实际应用中要考虑到噪声的情况，无法得到上述精确的对应关系，一般使用近似值来估计传播算子矩阵P：

得到传播算子的估计值后，对其进行重构：

取Pxx的前N行得到矩阵Px1，由式（12）和式（20）可得[15]：

分别取Pxx的后N行、Pxy的前（N-1）行和Pxy的后（N-1）行得到矩阵Px2、Px3、Px4。定义矩阵：

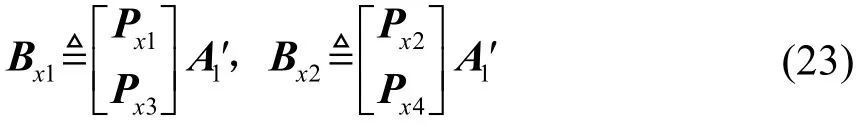
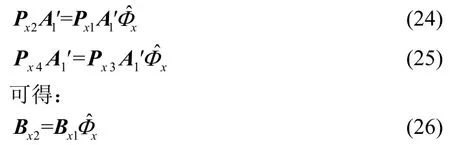
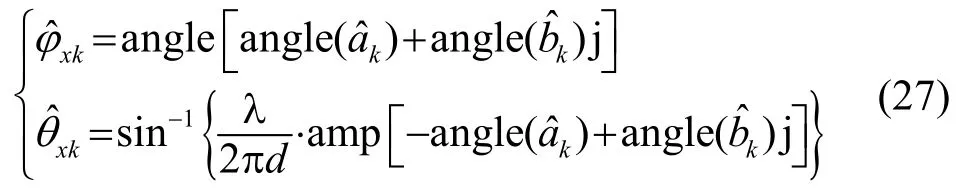
其中，amp（·）表示取幅度值，angle（·）表示取相角值。同理可得y轴方向平行线阵的二维DOA估计结果。

将两个方向的平行线阵进行并行处理方式，独立进行DOA估计，当两个独立估计结果得出后，进行融合操作，提高DOA估计精度。

融合规则：第m次蒙特卡洛实验得到的估计结果，将两个方向方位角和俯仰角的估计值进行均值处理，得到最终DOA角度估计结果。

算法具体实现步骤总结如下：

（1）根据式（15）构建协方差矩阵；

（2）式（18）和（19）利用协方差矩阵分解重构得到估计值P和Pc；

（3）对矩阵pc分解重构得到Px1、Px2、Px3、Px4，并且得到bk和A′；

（5）同理进行y轴方向平行阵的参数计算，基于y轴方向平行线阵进行二维DOA估计；

（6）结果融合得到双平行线阵的DOA估计结果。

2 仿真分析

为验证本文算法的性能指标，使用Matlab仿真软件对算法进行仿真。仿真中，所采用的双平行线阵的两个子阵阵元数分别为4和3，仿真使用水下通信定位信号的频率为37.5 kHz，对应的阵列阵元间距为1 cm，进行算法性能测试。采用求均方根误差（Root Mean Square Error,RMSE）作为衡量算法DOA估计性能的标准，定义为

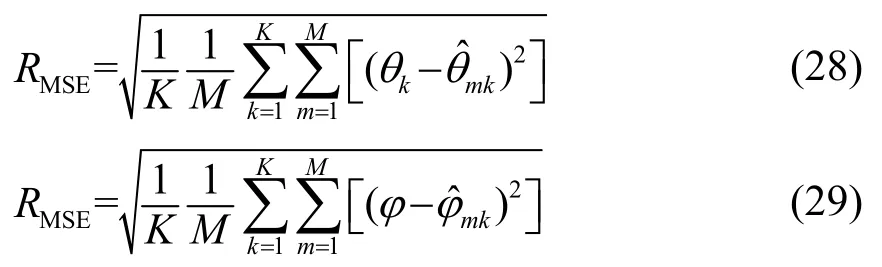
式中：M表示蒙特卡洛实验次数，θmk和φmk分别表示第m次实验中、第k个信号的估计值。仿真结果中误差单位均为（°）。

2.1 估计效果测试

图2给出了在信噪比（Signal to Noise Ratio,SNR）为15 dB的情况下，进行200次蒙特卡洛实验，快拍数S=200，信源数K=3，角度分别为（−25°,45°）、（5°,15°）和（30°,60°）时算法的仿真情况。

从图2可以看出，本文采用的算法在设置条件下可以较好地对目标方位进行估计，得到的DOA估计结果基本和目标位置吻合，验证了本文所使用高频通信信号配合小尺寸阵列进行水下DOA估计的可行性。

图2 SNR为15dB情况下双平行线阵及传播算子算法的二维DOA估计结果（S=200,K=3）Fig.2 Two-dimensional DOA estimation result of double parallel linear arrays and propagator method when SNR is 15 dB （S=200,K=3）

2.2 估计误差随参数变化情况

下面测试算法的多源信号估计性能，进行 200次蒙特卡洛实验，快拍数为200，计算均方根误差，仿真结果如图3所示。

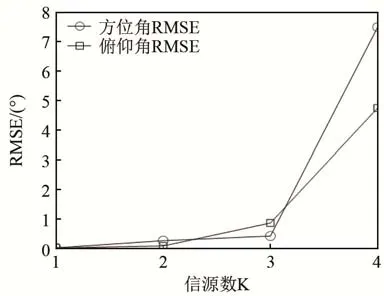
图3 SNR为15dB情况下DOA估计的均方根误差随信源数变化情况（S=200）Fig.3 Variation of RMSE of DOA estimation with number of sources when SNR is 15 dB （S=200）

从图3可以看出信源数对本文所用水下DOA估计算法的影响，由于本文采用小尺寸阵列，子阵阵元数分别为4和3，进而当信源数为4时，由于阵元个数的限制，本文算法精度下降。当信源数小于4时，本文算法在考虑小尺寸阵列的情况下有较好的估计效果。图4、5测试了算法估计误差随快拍数和信噪比的变化情况。

从图4～5可以看出，与图3相对应，在SNR为15 dB、S=200的条件下，对于3个目标的估计RESM最大在1°左右，有较好的估计效果。

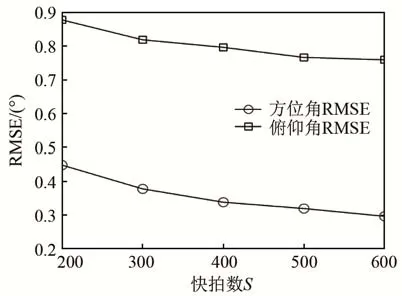
图4 SNR为15 dB情况下DOA估计的均方根误差随快拍数变化情况（K=3）Fig.4 Variation of RMSE of DOA estimation with number of snapshots when SNR is 15 dB （K=3）

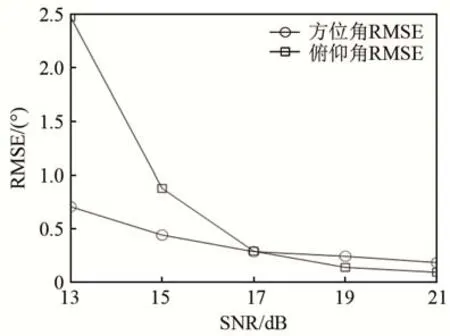
图5 DOA估计的均方根误差随SNR变化情况（K=3,S=200）Fig.5 Variation of RMSE of DOA estimation with SNR（K=3,S=200）

3 结 论

本文为解决集群AUV水下协同工作所遇到的定位问题，并且满足AUV水下平台对于小尺寸、低功耗的要求，提出了一种双平行线阵结合PM方法的二维水下DOA估计算法，利用双平行阵列融合提高了一定的估计精度；使用PM算法，避免二维谱峰搜索造成的大量计算，实现了二维角度自动配对，降低了复杂度，从而达到低功耗要求；采用通信与水下定位一体化方法，利用高频通信信号作为定位信号源，使用小尺寸基阵，开展集群 AUV水下定位方法，对多源信号估计精度较好，满足了集群AUV协同工作时的定位要求。本文所采用的阵列结构简单，算法复杂度较低，对整个系统功耗控制较好，在载体限制阵列尺寸以及平台低功耗的要求下，有较好的角度估计性能。