基于跟踪起始准则的多基地声呐阵位优化算法

陈芳香，卢术平，丁 烽

（杭州应用声学研究所，浙江杭州 310023）

0 引 言

现代反潜战中，随着目标潜艇降噪和消声技术的发展，以及滨海船只和水下设施的增加，使得传统单站被动或主动声呐难以有效探测并跟踪到潜艇[1-2]。而多基地声呐系统利用其多主动发-收节点组合和空间分集特性，不仅提高了目标数据率，而且提供了多角度的目标主动回波。同时，多基地声呐通过集中式或分布式融合处理，能够进一步提高目标的定位精度，增大信噪比，提高水下目标跟踪的稳健性、互补性[3-4]。

多基地声呐监测区域范围较大，拓扑结构复杂多样，不同的多基地声呐阵位结构导致探测性能迥异。因此，阵位优化是成功应用多基地声呐系统的关键技术之一。研究的基本思路是针对某一监视区域，根据实际需求最大化或最小化特定指标函数，进而得到针对特定指标的优化发射、接收声呐节点的空间位置。目前常用的多基地声呐阵位优化主要采用两类静态配置方法，一类是以多基地声呐探测区域覆盖最大为原则，如卡西尼卵形线多基地声呐配置方法、优势区探测方法等[5-10]。另一类则考虑利用时序、波形等要素，基于探测性能或者系统跟踪性能等最大化的声呐配置方法[11-17]。文献[5]中Ngatchou运用Cassini卵形线来代替声学模型，基于序贯粒子群（Sequential Particle Swarm Optimization,SPSO）算法确定多基地声呐传感器的最佳数量和阵位方案，但建立的模型较实际有较大差异。文献[12]中，David利用贝叶斯准则以及基于跟踪质量、带宽多样性的智能发射时序控制方法来确定多基地声呐最优配置策略，该策略适用于一般的搜索场景，并不能用于航迹维持场景。

针对水下区域的监视问题[18-19]，仅仅考虑以单帧回波为基础的目标检测概率或以多帧为基础的运动目标持续跟踪精度等指标，都难以反映实际区域的搜索监视需求；而能够在目标跟踪过程中获得成功起始航迹，是衡量有效搜索的关键。所以本文在集中式和分布式两种多基地融合处理架构下，利用区域跟踪起始覆盖概率指标来衡量多基地阵位优化效果，该指标综合反映了目标检测和跟踪性能。此外，由于构建的多基地阵位优化模型为多维高阶非凸数学问题模型[7]，本文将采用粒子群优化（Particle Swarm Optimization,PSO）算法。粒子群优化算法具有原理相对简单、可调整参数较少、容易实现、对软硬件要求较低及适用性强等优点，且在实现上不需要极大的迭代次数，在较短时间内就能得到最优解或近似最优解[20-21]。最后得到区域跟踪起始覆盖率最大化的全局最优多节点基地声呐阵位。仿真结果表明，在不同的跟踪融合准则下，优化后的多基地声呐节点阵位对应得到的跟踪起始覆盖率比典型经验方案都有较大提高。

1 多基地声呐阵位优化问题建模

本节首先简要介绍声呐节点跟踪起始概率计算准则，然后推导出两种多基地融合模式下的跟踪起始概率计算准则，最后给出基于跟踪起始准则的多基地声呐阵位优化问题数学模型。

1.1 跟踪起始概率计算准则

在声呐系统中所有声源完成连续多次发射后，获得所有发-收节点处的检测结果，再利用检测概率值并基于一定的准则计算跟踪起始概率，然后依据跟踪起始概率值来确定是否起始跟踪。

尽管已经存在很多类型的跟踪起始概率计算准则[22]，声呐场常用的准则是“当连续n次中有超过m次检测到目标，则起始跟踪”，即m-in-n准则。在该准则下，本地跟踪起始概率pti的定义为：在n次ping后起始跟踪的概率，该概率值依赖于选定的m值，且m≤n。

考虑包含收发共置的单个声呐的系统，基于上述准则，本地跟踪起始概率的计算表达式为[22]

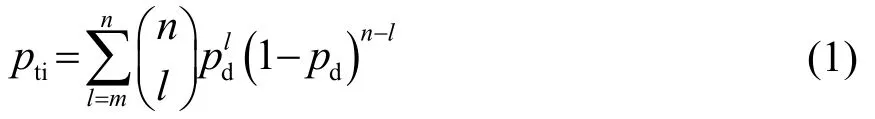
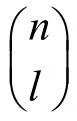
当m=3，n=5时（在5次连续ping后，检测到目标的发-收节点对为3），基于式（1）可计算得到：

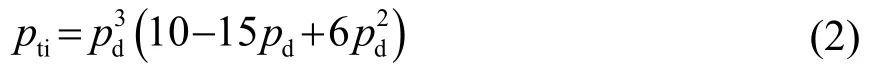
图1给出了基于不同m和n值时（m-in-n），针对单个声呐，起始跟踪概率pti与检测概率pd的变化关系。

这里假设跟踪融合是在检测之后，且只考虑检测到目标的概率，而不考虑虚警概率的影响。

图1 基于不同m和n值，pti与pd的变化关系Fig.1 The relationship betweenpti andpd for different m and n

1.2 基于m-in-n准则的声呐场跟踪起始概率

首先给出四种跟踪融合处理模式下，基于单次ping检测概率的跟踪起始概率计算式。假设同一声源所有ping对应得到的检测概率相等，且每次ping都是统计独立的。本节针对3-in-5准则展开讨论,其他准则的对应讨论类似。本节中单基地表示系统中声呐是收发共置工作模式；多基地表示系统中接收声呐可接收所有发射声呐的回波信号；分布式表示每个声呐独立处理各自的数据；集中式表示系统中所有声呐的数据首先传输至处理中心，再在中心统一处理；跟踪融合为将跟踪起始概率数据进行处理，分为分布式融合和集中式融合。

1.2.1 单基地分布式融合模式

假设声呐场包含J个单基地声呐，每个声呐独立进行跟踪融合处理。跟踪起始概率的计算公式如式（3）所示[22]：

式中，pti,j表示声呐j在5次ping后的起始跟踪概率，利用声呐节点的探测概率pd，基于式（1）可计算得到pti,j。

1.2.2 单基地集中式融合模式

每个接收节点只接收来自共置声源的回波信号，但是检测信息被传输到跟踪处理中心节点。为了与 1.2.1节中的单基地分布式跟踪融合作对比，下面我们都考虑声呐场中每个声源的5次ping，但是中央节点根据任意三次检测决定是否起始跟踪，每次检测的来源可以是任一声源的任一次 ping的结果。

最简单的声呐场跟踪起始概率的计算方式是首先考虑跟踪不能被成功起始的概率，再得到成功起始跟踪概率[22]：

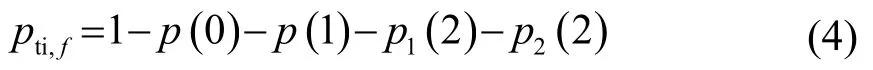
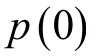
式中，pd,j表示接收节点j的检测概率，J表示声呐场中发射节点总个数。

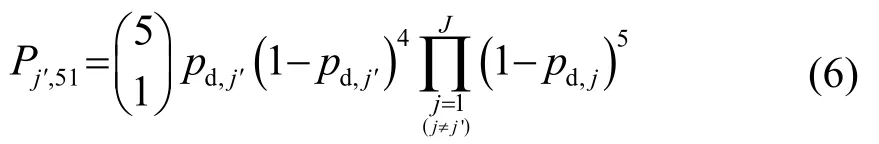
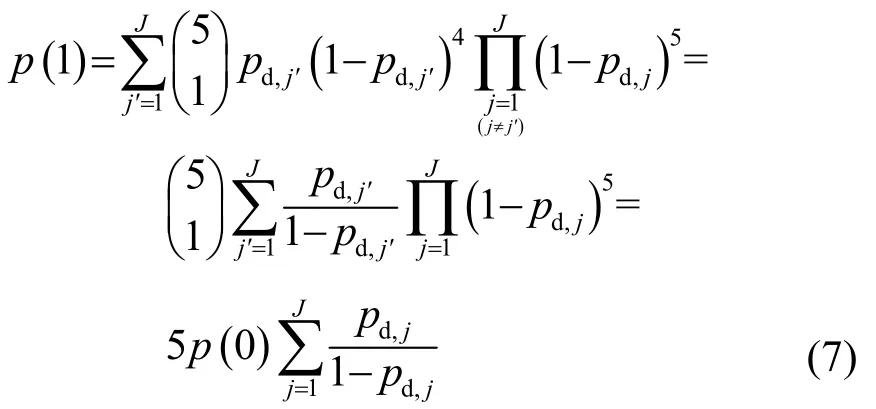
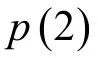
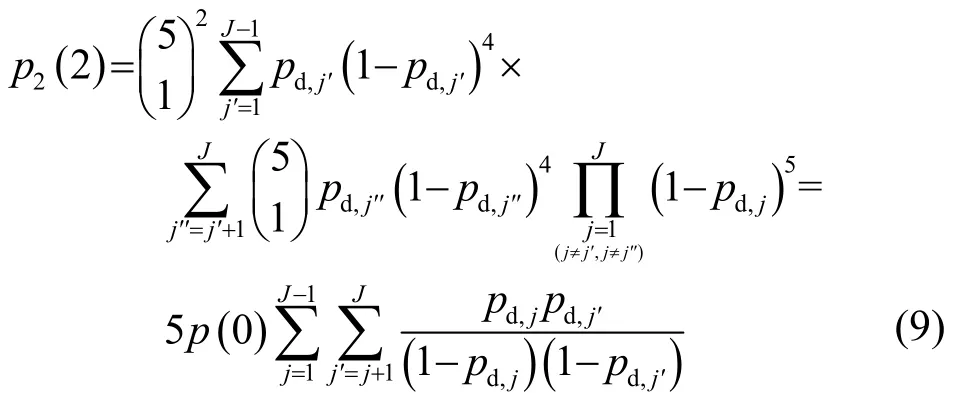
1.2.3 多基地分布式融合模式

在多基地声呐场中，每个接收节点接收任意声源5次ping的回波信号，但是在接收节点处独立完成跟踪起始。在声呐场中所有声源完成5次ping后，计算跟踪起始概率。针对接收节点j，其跟踪起始概率的计算式为[22]

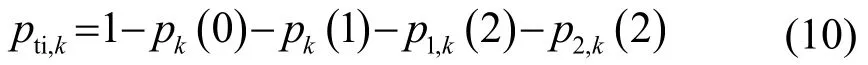
式（11）和式（12）中，pd,jk表示接收节点k接收到发射节点j的回波信号对应得到的检测概率。

p1,k（2）表示针对指定声源的5次ping后，接收节点k完成两次检测且没有其他声呐节点做到成功检测的概率，与式（8）类似：

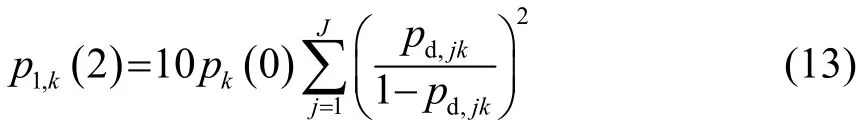
p2,k（2）中包含的两次检测来源于不同的两个声源，其计算类似于式（9）：

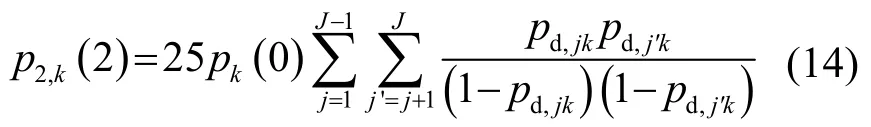
最终，根据所有接收节点的跟踪起始概率，得到声呐场的跟踪起始概率为[22]

1.2.4 多基地集中式融合模式

在声呐场中，每个接收节点接收任意声源5次ping的回波信号，并将检测信息传输至中心节点完成跟踪起始。计算思路与单基地类似，此处需要注意包含两次检测的概率有四种情况。多基地集中融合模式下，跟踪起始概率表示为[22]

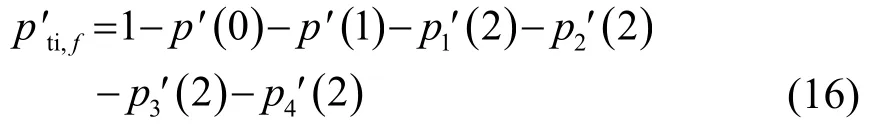
p′（1）的计算与式（7）类似，假设检测是由发射节点j′与接收节点k′对应完成，则：

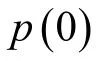
p1（2）的计算与式（8）类似，其中两次检测都是由同一发-收对完成的：

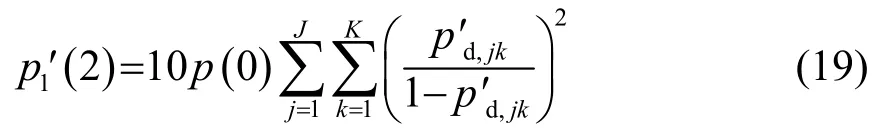
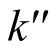
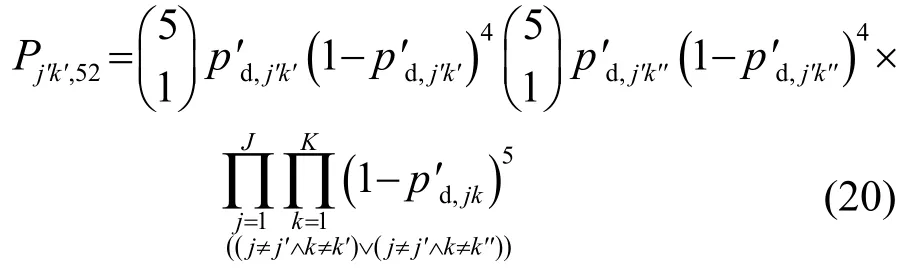
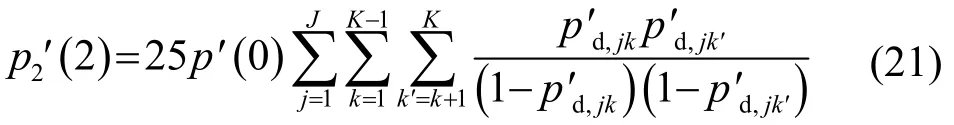
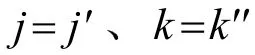
当发射节点个数和接收节点个数K不等时，图2给出了几种不同的节点配置，在分布式和集中式跟踪融合处理模式下，跟踪起始概率与检测概率的变化关系。这里选择单个节点结果作为参照。

由图2可看出，当接收节点数量较少时，跟踪起始概率随着发射节点数量的增加明显增大；当接收节点增大到一定值时，随着检测概率增大，对于提高跟踪起始概率这一目标而言，分布式跟踪融合模式性能明显差于集中式跟踪融合模式，如图2（d）中所示，接收节点数为10时，发射节点为1的集中式性能逼近发射节点为3的分布式跟踪融合模式。

1.3 多基地声呐阵位优化数学模型

根据以噪声为主要背景干扰的声呐方程、信号检测理论计算得到多基地声呐场中针对发射节点j和接收节点k探测概率的计算公式为[7]

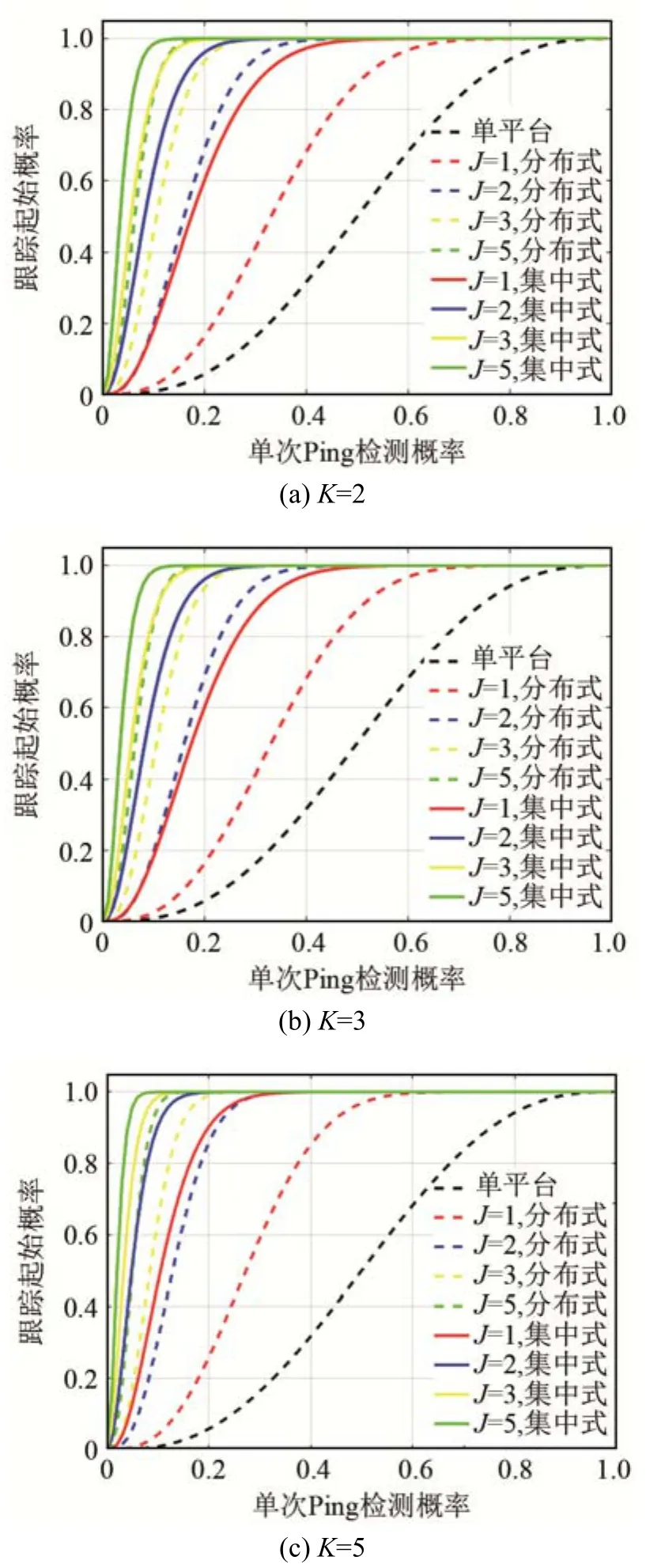
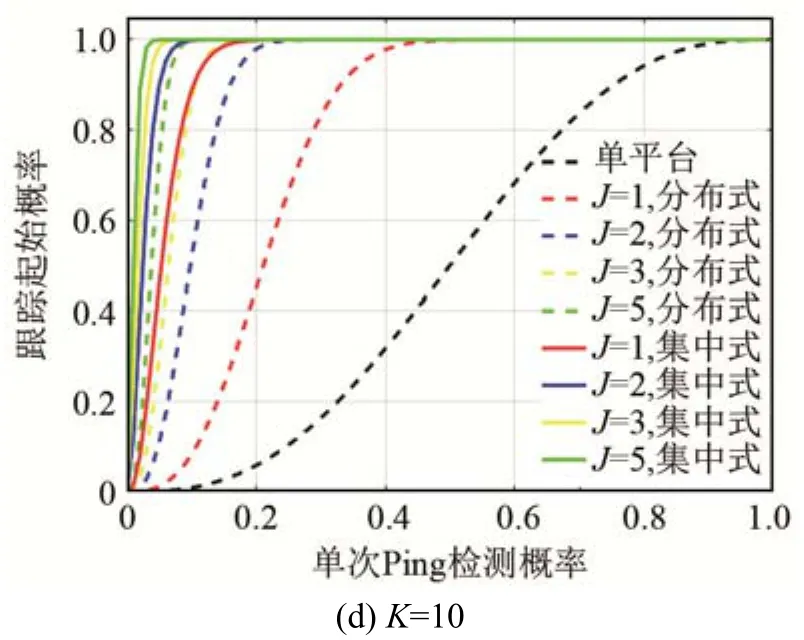
图2 接收节点个数固定，发射节点个数变化时，pti与pd的变化关系Fig.2 The relationship betweenpti andpd when the number of receivers is fixed and the number of transmitters is variable

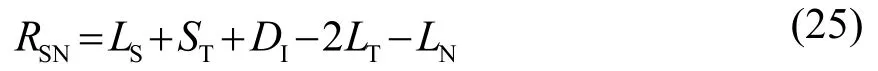
式（25）中，LS表示声源级；ST表示目标强度，根据一定的目标强度模型计算得到；DI表示指向性系数；LT表示单向传播损失；LN表示噪声级。通过建立检测概率计算模型，结合检测概率计算式（24），可得对应节点处的检测概率。

在得到发收节点的检测概率后，利用1.2中的公式计算对应跟踪处理模式下的跟踪起始概率。

在监测区域V内考虑阵位优化问题，将该区域划分成Q个网格点来代表假设的目标位置。在给定区域V中，K表示声呐接收节点个数，J表示发射节点的个数（单基地模式下J=K），假设目标位于网格点的中心，对于每个发射-接收节点对，计算每个网格点对应的跟踪起始概率。

分布式和集中式多基地融合模式下，成功跟踪起始覆盖率都定义为

式（27）中，pthreshold表示跟踪起始概率的门限值，高于该门限的定义为成功起始，覆盖率定义为成功起始的网格数与网格总数的比值。

2 粒子群算法

2.1 PSO算法介绍

粒子群算法（Particle Swarm Optimization，PSO）是20世纪90年代兴起的一门学科[19]，因其概念简明、实现方便、收敛速度快而为人所知。粒子群算法的基本思想是模拟鸟群随机搜寻食物的捕食行为，鸟群通过自身经验和种群之间的交流调整自己的搜寻路径，从而找到食物最多的地点。

粒子群算法与遗传算法有很多相似之处，其收敛于全局最优解的概率很大。粒子群算法具备以下优点：

（1）相较于传统遍历搜索算法，其计算速度非常快，全局搜索能力也很强；

（2）对于种群大小不十分敏感，所以初始种群大小设定不同对速度影响不大；

（3）适用于连续函数极值问题，对于非线性、多峰问题均有较强的全局搜索能力。

2.2 面向多基地阵位优化的PSO算法

PSO算法中每个粒子在搜索空间中单独地搜寻最优解，并将其记为当前个体极值Pbest，并将个体极值与整个粒子群里的其他粒子共享，找到最优的个体极值作为整个粒子群的当前全局最优解Gbest。粒子群中的所有粒子根据自己找到的当前个体极值Pbest和整个粒子群共享的当前全局最优解Gbest来调整自己的速度和位置。粒子群算法的思想相对比较简单，主要分为：

（1）初始化粒子群；

（2）评价粒子，即计算适应度值；

（3）寻找个体极值Pbest；

（4）寻找当前全局最优解Gbest；

（5）修改粒子的速度和位置。

粒子群算法的基本流程如图3所示。

速度和位置更新是粒子群算法的核心，其原理表达式为[20]

式中：w为惯性权重；t是当前迭代次数；pi为个体最优粒子位置；pG为全局最优粒子位置；φ1为粒子学习因子，φ2为群体学习因子；rand（·）为在一定范围内产生随机数的随机函数。

当最大化的适应度函数F满足：

个体和全局最优粒子根据式（30）进行位置更新：

利用PSO算法来处理数量确定的多基地声呐阵位优化问题具备较大的自由度，可以叠加不同类型的约束，这些约束仅需修正适应度函数（面积、形状覆盖范围，不同环境因素等）来实现。

图3 粒子群算法基本流程Fig.3 The basic process of the particle swarm optimization algorithm

基于粒子群算法，得到全局最优多节点阵位方案的步骤如下：

（1）初始化粒子群算法相关参数，包括粒子维数、种群大小、最大迭代次数、算法终止条件等；

（2）初始化每个粒子位置（单个粒子位置代表一种阵位方案）及速度；

（3）计算每个粒子提供候选阵位方案的目标函数（成功跟踪起始覆盖率），即个体适应度值；

（4）令各粒子初始位置为粒子初始个体最优；

（5）比较得到个体适应度值最大的粒子为全局最优粒子；

（6）利用式（28）更新所有粒子的位置及速度；

（7）重新计算每个粒子提供的候选阵位方案的目标函数（成功跟踪起始覆盖率）；

（8）更新所有粒子的个体最优：

计算当前每个粒子提供的阵位方案的目标函数，即个体适应度值，与原有阵位方案对比，选出更优方案作为个体最优阵位方案；

（9）若不满足终止条件，则重复步骤（3）～（8）；若满足算法终止条件或达到最大迭代次数，则输出多节点阵位方案作为全局最优阵位方案。

多基地声呐阵位优化方案的流程图如图4中所示。

3 数值仿真

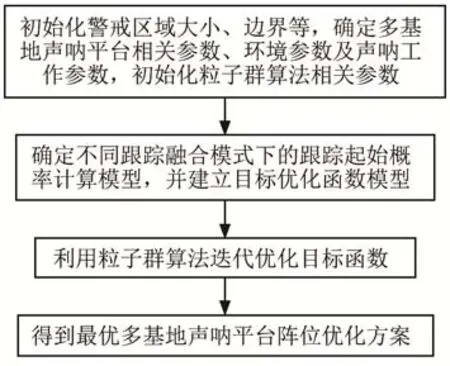
图4 多基地声呐阵位优化方案流程图Fig.4 The computation process of the placement optimization method for multistatic sonar

首先在发射声呐节点个数为2、接收节点个数为2，发射节点个数为4、接收节点个数为8这两种场景下，验证在多基地分布式和多基地集中式跟踪融合处理模式下，利用粒子群算法得到的多基地阵位优化方案的成功跟踪起始覆盖率与检测概率分布情况，并与典型阵位方案以及随机阵位方案作对比。这里典型阵位方案为根据经验确定的一种方案，通常设定为较为对称的阵位，随机阵位表示对发射及接收节点的位置进行随机生成。另外，当收发节点个数变化时，在分布式和集中式跟踪融合处理模式下，得到优化阵位方案对应的目标成功跟踪起始覆盖率的对比曲线。

3.1 多基地分布式跟踪融合

在多基地分布式跟踪融合处理模式下，当发射节点个数为2、接收节点个数也为2时，得到基于粒子群算法的覆盖率随迭代次数变化曲线如图5所示，优化阵位方案与典型阵位方案区域成功跟踪起始概率的分布情况如图6所示，图中蓝色五角星表示发射节点，绿色圆圈表示接收节点。

当发射节点个数为4、接收节点个数为8时，得到基于粒子群算法的覆盖率随迭代次数变化曲线如图7所示，优化阵位方案与典型阵位方案区域成功跟踪起始覆盖分布情况如图8所示。

由图5和图7可见，随着迭代次数的增加，多基地分布式跟踪起始覆盖率逐渐提高直到收敛，当发射节点个数为4，接收节点个数为8时，收敛后跟踪起始覆盖率约为83%，相比较起始状态，提升了25%。由图6和图8可见，优化后的多基地声呐阵位相比典型阵位方位，其跟踪起始概率都有较大提高。图6和图8中，覆盖率分别从4.69%和42.54%提升到38.6%和85.44%。因此，分布式架构下优化后多基地声呐阵位布置方案效果有明显提升。

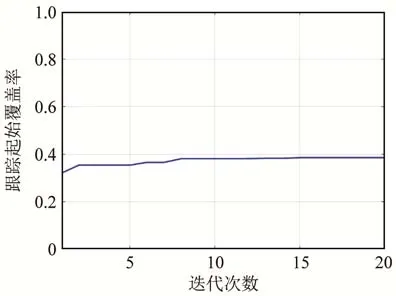
图5 目标跟踪起始覆盖率随着迭代次数变化的曲线（分布式跟踪融合，发射和接收节点都为2）Fig.5 The curve of target track-initiation coverage rate varying with iteration times under distributed tracking fusion mode of 2 transmitters and 2 receivers

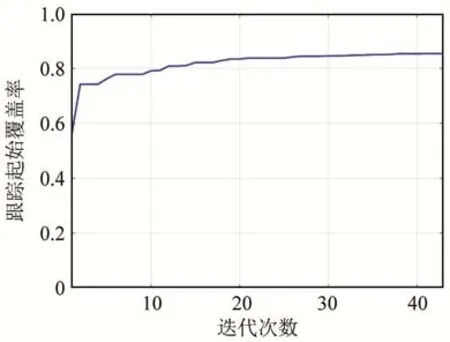
图7 目标跟踪起始覆盖率随着迭代次数变化的曲线（分布式跟踪融合，发射节点为4和接收节点都为8）Fig.7 The curve of target track-initiation coverage rate varying with iteration times under distributed tracking fusion mode of 4 transmitters and 8 receivers

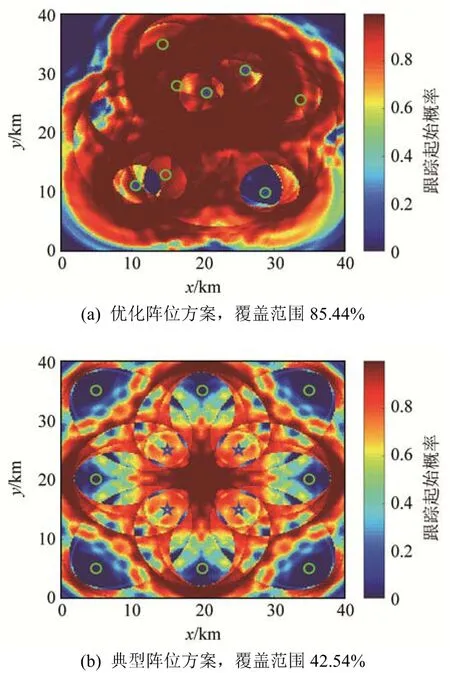
图8 在图7所示的条件下阵位优化方案与典型阵位方案的跟踪起始概率分布图对比Fig.8 Comparison of target track-initiation probability distribution between the optimized sonar placement scheme and the empirical one under the conditions shown in Fig.7

3.2 多基地集中式跟踪融合

在多基地集中式跟踪融合处理模式下，当发射节点个数为2、接收节点个数为2时，得到基于粒子群算法的覆盖率随迭代次数变化曲线如图 9所示，优化阵位方案与典型阵位方案区域成功跟踪起始覆盖分布的情况如图10所示。

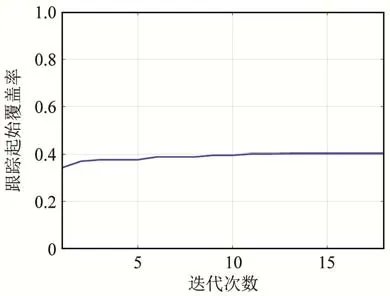
图9 目标跟踪起始覆盖率随着迭代次数变化的曲线（集中式跟踪融合，发射和接收节点都为2）Fig.9 The curve of target track-initiation coverage rate varying with iteration times under centralized tracking fusion mode of 2 transmitters and 2 receivers

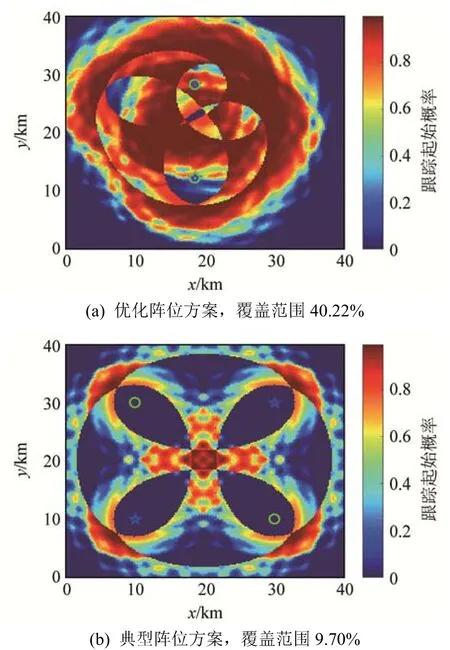
图10 在图9所示的条件下阵位优化方案与典型阵位方案的跟踪起始概率分布图对比Fig.10 Comparison of target track-initiation probability distribution between the optimized sonar placement scheme and the empirical one under the conditions shown in Fig.9

当发射节点个数为4、接收节点个数为8时，得到基于粒子群算法的覆盖率随迭代次数变化曲线如图 11所示，优化阵位方案与典型阵位方案区域成功跟踪起始覆盖分布的情况如图12所示。

同样地，从图9～12可见，集中式架构下优化后多基地声呐阵位布置效果相比较随机初始化方案和典型阵位方案都有明显提升。由图10和12可见，优化后的集中式多基地声呐阵位相比典型阵位方位，其跟踪起始概率覆盖率分别从 9.70%和63.90%提升到40.22%和93.40%。

图11 目标跟踪起始覆盖率随着迭代次数变化的曲线（集中式跟踪融合，发射节点为4和接收节点都为8）Fig.11 The curve of target track-initiation coverage rate varying with iteration times under centralized tracking fusion mode of 4 transmitters and 8 receivers

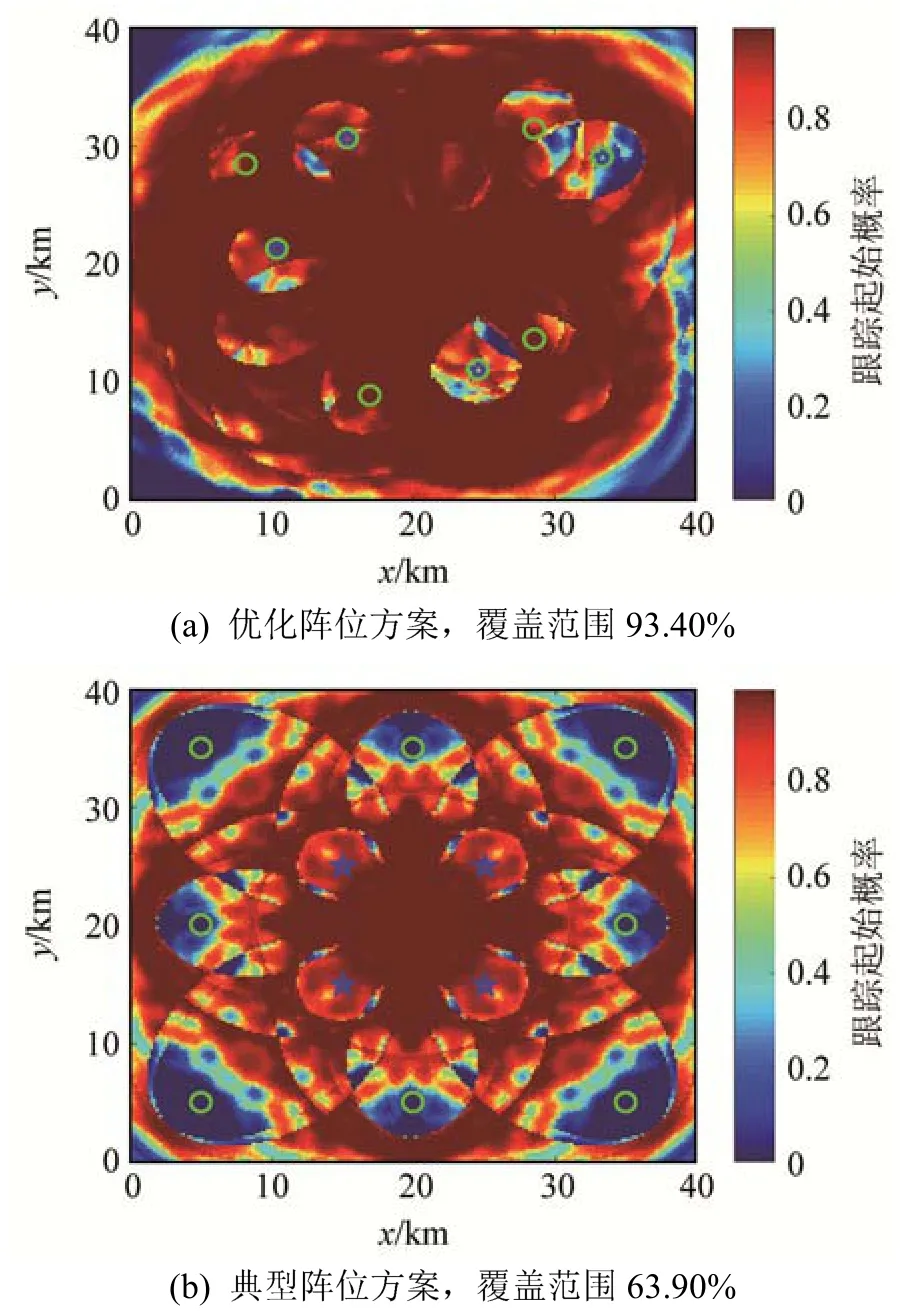
图12 在图11所示的条件下阵位优化方案与典型阵位方案的跟踪起始概率分布图对比Fig.12 Comparison of target track-initiation probability distribution between the optimized sonar placement scheme and the empirical one under the conditions shown in Fig.11

3.3 分布式与集中式对比

表1为两种多基地模式下，多基地阵位优化方案与典型阵位方案以及随机阵位方案的成功跟踪起始覆盖率值。

表1 分布式和集中式两种跟踪融合模式下的成功目标跟踪起始覆盖率Table 1 Successful target track-initiation coverage rate for distributed and centralized tracking fusion modes

从表1中可见，在2发2收和4发8收的场景下，不论是分布式还是集中式融合处理方式，优化阵位方案的跟踪起始覆盖效果较典型阵位和随机阵位方案都有显著提升，且集中式架构下优化阵位、典型阵位，以及随机方案阵位较分布式都更优。

发射节点个数选定为2、3、5、8，接收节点个数在 1～8范围内变化时，在多基地分布式和集中式跟踪融合处理模式下，基于粒子群算法优化多基地声呐场的节点空间位置，得到的收敛后的区域成功跟踪起始覆盖率的对比曲线如图13所示。

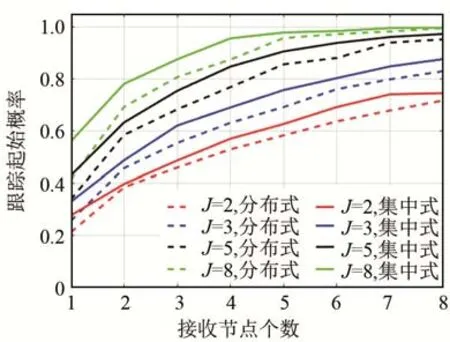
图13 多基地不同分布式与集中式跟踪融合处理模式下目标跟踪起始覆盖率随接收节点数的变化关系曲线对比Fig.13 Variation curves of the target track-initiation coverage rate with the number of receivers under different distributed and centralized tracking fusion modes in multistatic sonar system

由图 13可见，在集中式和分布式架构下，发射节点相同时，接收节点增加，区域成功跟踪起始覆盖率也都随之增大，接收节点相同时，发射节点增加也会使得覆盖率增大；在相同声呐节点配置条件下，集中式模式下得到的覆盖效果优于分布式。

4 结 论

本文提出了一种基于跟踪起始准则的多基地声呐节点阵位优化算法。该算法在集中式和分布式两种模式下，根据多基地声呐的跟踪起始融合架构，建立了以区域目标跟踪起始覆盖率为指标的阵位优化模型，并采用粒子群算法优化，最大化区域跟踪起始覆盖率，从而得到全局最优多发-收声呐节点的空间阵位。仿真实验结果表明，该算法有效、可行。在分布式和集中式两种处理模式下，优化阵位的覆盖效果优于典型阵位和随机阵位方案，集中式处理模式下的效果优于分布式。