基于时序关联性的定制订单接受决策研究
丁龙晨芷,彭紫荆
(1.武汉理工大学 物流工程学院,湖北 武汉 430063;2.武汉大学 经济与管理学院,湖北 武汉 430072)
近年来,随着互联网技术的应用和发展,制造业逐渐趋向智能化、柔性化、个性化,消费互联网随之向产业互联网转变。消费者在电子商务平台上提交个性化订单,制造商对平台收到的订单进行处理并制定生产计划进行生产,在约定的交货期限内完成订单并交付。由于企业产能有限,只能选择接受部分订单来加工生产,过多地接受订单会造成订单无法按时保质完成,甚至造成企业声誉损失和客户流失。
个性化定制模式可以在满足消费者多样化需求的同时增强企业核心竞争力。贾赵捷[1]通过文献分类归纳将个性化定制模式分为C2M、C2D与D2C、C2B这3类。一些学者就有限产能、交货期、订单价格等因素对订单接受决策的影响进行了相关研究。周怡伶[2]分别就MTO企业接受竞争型订单和非竞争型订单情形下,建立订单接受决策方法。ARASH等[3]基于客户订单解耦点的位置,为混合生产策略开发了基于能力承诺的订单接受模型,有效减小延迟交货的风险。SUJAN[4]提出制造商与多个客户之间就交货期和订单价格进行谈判时引入中介程序以实现订单接受决策。赵瑞敏等[5]针对MTO生产企业引入订单等级因素,构建基于二次选择算法的决策模型,使得企业收益最大化。于超等[6]考虑交货违约风险传导情形构建描述订单产品交货违约事件的故障树,计算制造商接受订单的预期收益,以此得到订单接受决策。LENG等[7]提出一种深度学习算法进行精确预测,并将预测结果与原订单特征结合得到基于强化学习的订单接受决策。考虑数据时序特性的规则称为时序关联规则。刘一[8]采用聚类分析进行时间粒度的划分,将统计分析和自组织映射神经网络的时间粒度划分方法应用到时序关联规则挖掘算法中。邓毅[9]综合考虑订单的总收益和机会风险成本,建立时序关联的订单选择模型,使得企业通过改变订单流来获取更高的利润。
鉴于此,笔者考虑当前计划期内订单与未来计划期内订单之间存在的时序关联性,以及定制订单生产过程中存在的转换成本和转换时间,研究产能有限企业的长期利润最大化的订单接受决策问题,对企业的可持续稳定发展有重要的现实意义。
1 问题描述及模型假设
企业在生产计划期初收到多个订单,但是其生产能力无法满足所有订单需求,只能接受部分订单进行生产。虽然计划期内某些订单的当前收益并不高,但是考虑到个性化定制订单在未来会以一定概率引致高收益的订单需求,因此企业需要综合考虑当前计划期内订单的当前收益和该订单在未来可能引致的订单收益,从当前收到的订单中选择接受最佳的订单组合,充分利用企业有限产能以实现长期总利润的最大化。订单接受决策逻辑关系图如图1所示。
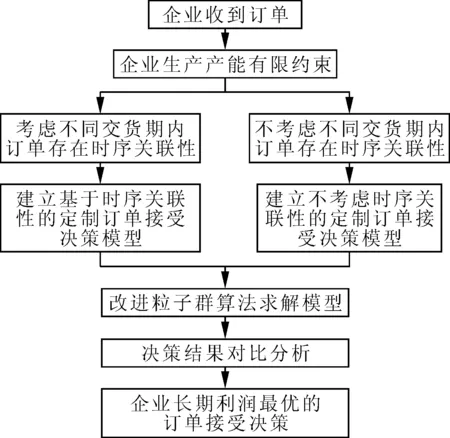
图1 逻辑关系图
笔者在一定假设条件的基础上研究加工装配型企业的个性化定制订单接受决策问题。虽然这些假设与实际情况存在一定的差距,但是提出的订单接受决策模型是从个性化定制订单生产的特点出发,以企业的长期利润最大化为目标,考虑订单之间存在时序关联性,建立个性化定制订单接受决策模型。主要的模型假设如下:
假设1个性化定制订单中产品均不同,且每阶段内到达的订单在制定生产计划之前已到达。
假设2订单生产过程不容中断,且在单个生产线上加工完成,定制化产品所需原材料、零部件供应充足。
假设3所有选择接受的订单必须在该计划期内完成,若推迟到以后的计划期,企业将无法获得订单收益,并面临违约赔偿。
假设4该企业的生产加工系统单位时间内消耗产能的速度是均匀的,即企业的最大产能可以用计划期的总时长来表示。
假设5订单收益、生产数据和不同计划期内订单时序关联规则均已知。
2 基于时序关联性的定制订单接受决策模型
首先对订单接受决策模型符号进行说明,并分析决策模型的目标函数和约束条件,在此基础上提出考虑企业产能有限、基于时序关联的定制订单接受决策模型,并以此提出改进粒子群算法求解模型。
2.1 符号说明
n为当前计划期收到的总订单数;N={1,2,…,n}表示当前所有待接受订单集合,1,2,…,n为订单编号;Pi为订单i在当前计划期内的收益,即当前收益;Pwi为接受订单i在未来可引致的订单收益,即未来期望引致收益;αi为订单i与未来引致订单之间的时序关联置信度;ti为订单i的生产加工时间;T为当前计划期的总时长;ci为订单i的生产加工成本;czi为订单i的生产加工前的转换成本;tzi为订单i的生产加工前的转换时间。
2.2 模型的建立与分析
在加工装配型生产企业的背景下,考虑当前计划期内订单与未来计划期内订单之间存在时序关联性和个性化定制订单的生产加工特点,在单个生产线的研究背景下,以计划期内企业的总利润最大化为目标,建立个性化定制订单接受决策模型。
(1)决策变量。xi为订单接受决策变量,若订单i被接受,则xi=1,否则xi=0。
(2)目标函数。由于个性化定制订单具有小批量、多品种的特点,考虑当前计划期内不同订单生产过程中存在不同的转换时间和转换成本,所以总利润由4个部分组成:企业选择接受的订单当前收益W1、订单的未来期望引致收益W2、订单总生产加工成本C1、订单生产加工前的总转换成本C2。因此,模型的目标函数可表示为:
maxW=W1+W2-C1-C2
(1)
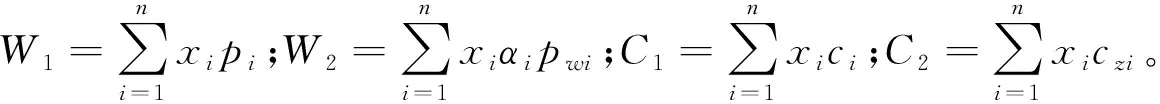
(3)约束条件。在进行订单接受决策时必须考虑企业的生产能力,超过产能约束,会给生产系统造成严重负荷,降低产品质量。因为企业产能有限,由上述假设可知该企业的生产加工系统单位时间内消耗产能的速度是均匀的,即企业的最大产能可以用计划期的总时长来表示,所以选择接受的订单在生产加工过程中消耗的总时间应该在企业的最大生产能力限制范围之内,即产能约束表达式为:
(2)
因此,以企业总利润最大化为目标的考虑时序关联性的个性化定制订单接受决策模型为:
xi∈{0,1},∀i∈N
2.3 模型的求解与算法设计
根据上述模型约束可以将此问题转换成背包问题,企业产能有限情况下,基于订单时序关联性,对一个时间段收到的订单进行选择接受决策,可以看作是具有容量约束的背包选择装入一定价值的物品使得总价值最大化的过程。粒子群算法通过初始化粒子数据,模拟粒子在空间中不断运动寻找最优解的过程,并在寻找的过程中记录自身和群体的最佳位置从而不断更新每个粒子的位置来寻找最优解,其参数少,容易实现,对于混合整数规划模型的求解有很明显的优势。
(1)原始粒子群算法。算法随机产生粒子的群体规模为N,其中每个粒子i(i=1,2,…,N)在D维空间中的坐标位置可表示为xi=(xi1,xi2,…,xiD),粒子i的移动速度可以定义为每次迭代中粒子移动的距离,用vi=(vi1,vi2,…,viD)来表示,于是粒子在第d(d=1,2,…,D)维子空间中的状态更新方程为:
(3)
(4)
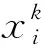
(2)粒子群算法的改进。一些学者提出粒子群算法存在一些缺陷,如算法后期容易陷入局部寻优、早熟收敛等。姚若侠等[10]结合贪心优化策略、模拟退火算法和离散二进制粒子群算法,提升种群寻优能力。耿亚等[11]基于直觉模糊熵,设置自适应惯性权重和变异策略,采用模拟退火机制得到更优地全局最优解,提高算法的鲁棒性和寻优能力。孙虎等[12]提出基于浓度抑制免疫粒子群算法和采用“经营替代”策略的粒子群算法用于装配作业车间调度问题。张莲等[13]提出自适应遗传粒子群算法,使得交叉概率和变异概率可根据每个个体对应的适应度函数值而自适应调整,提升寻优速度。综合上述学者对于粒子群算法的改进思路,笔者设置动态调整惯性权重并引入差分进化策略来提高种群后期多样性。
动态调整惯性权重是使其随着迭代次数的增加非线性减小,并通过一个符合贝塔分布的随机数对惯性权重的偏离程度进行调整,可以提高算法在迭代前期的全局搜索能力和迭代后期的搜索精度。粒子的速度更新公式如下:
ω=ωmin+(ωmax-ωmin)×
(5)
(6)
式中:t为当前迭代次数;tmax为最大迭代次数;σ为惯性调整因子;ωmax为初始的惯性权重;ωmin为算法最大迭代次数时的惯性权重。
针对算法后期种群多样性下降,容易陷入局部寻优的问题,笔者引入差分进化算法中的变异和交叉操作对粒子的位置进行更新,粒子位置更新公式如下:
(7)
式中:xr1,j、xr2,j、xr3,j为3个随机粒子个体,且r1≠r2≠r3;f为缩放因子;CR为交叉概率。
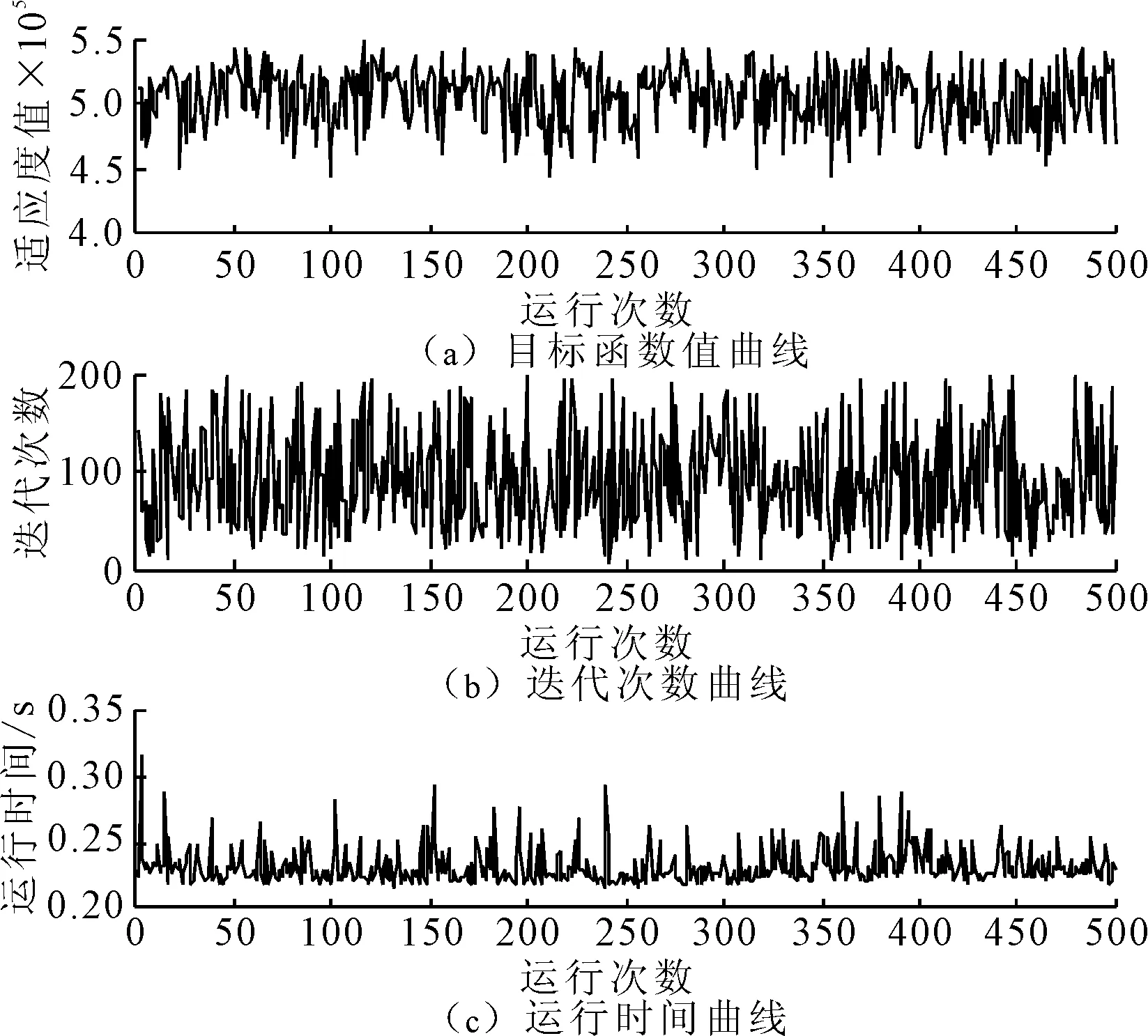
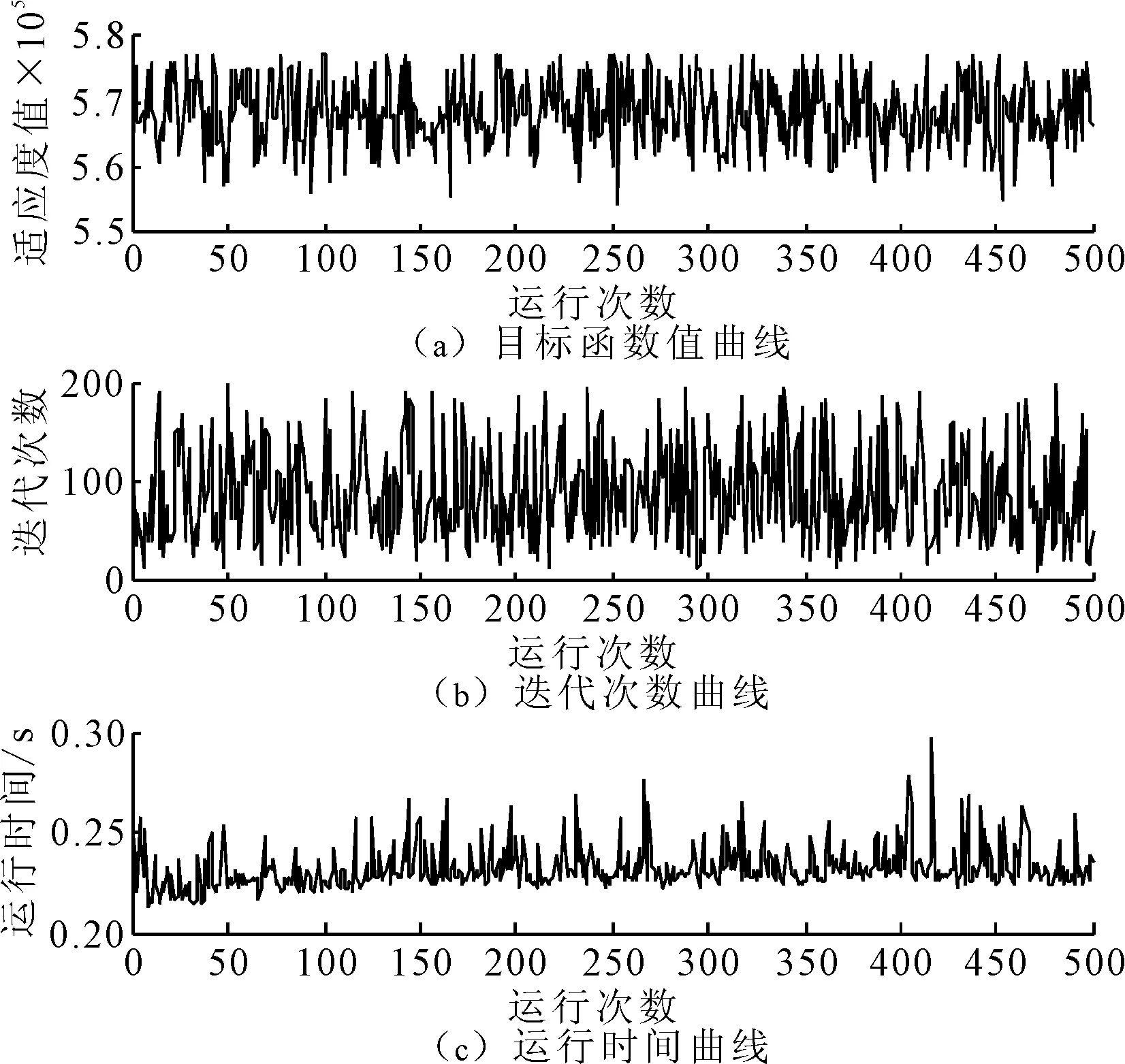
改进粒子群算法具体步骤:①初始化粒子种群数、最大迭代次数、种群中各微粒的速度和位置。将当前粒子的历史最优位置pbest作为初始位置,将gbest中的最优解作为粒子群全局最优位置。②计算每个微粒的目标函数,并存储每个粒子的位置和适应度值。③将每个粒子适应度值与其经历过的最好位置的适应度值进行比较,如果更好,则将其作为当前粒子的最好位置。④对每个粒子,从粒子种群中选择最好的适应度值的粒子位置作为种群的最好位置。⑤根据更新方程对粒子的速度进行更新,若rand 为了验证上述考虑时序关联性的全屋定制个性化订单接受决策模型(简称模型M*)的有效性,通过数值分析的方式来阐述上述模型,并设计了不考虑时序关联性的定制订单接受模型作为对照试验(简称模型M1),虽然该对照实验没有考虑订单未来引致的订单收益情况,但不代表时序关联关系不存在,只是在决策过程中没有考虑这一因素,并得到不同于模型M*的订单接受策略。 某家居企业拥有德国豪迈生产线,是一家集定制衣柜及其配套定制家具的研发设计、生产、销售的公司。为适应市场发展趋势,不断地改进其生产模式,从第1阶段的小批量定制化生产,到第2阶段的“标准件+非标准件”定制化生产模式,再到目前第3阶段的信息化和柔性化的大规模定制生产模式,大幅降低了生产成本,提高了应对市场需求的反应速度,其线上线下定制流程如图2所示。 图2 线上线下定制流程 考虑到订单具有配套的个性化定制的特性,订单之间常常存在时间序列关联关系。所以在企业产能有限的情形下,考虑订单的时序关联性进行订单的接受决策有助于企业长期发展的利润最大化目标的实现,在保证订单质量的同时使得企业长期收益率最大化。 研究数据取自该企业某一个生产计划指定前到达的定制衣柜订单数据,从中随机抽取30个定制衣柜订单。定制产品属性数据和订单加工生产相关信息如表1所示。 表1 订单数据信息 根据上述全屋定制个性化订单数据,模型参数设定如下:种群中粒子个数为100,最大迭代次数为200,学习因子均设为1.5,粒子运行速度最大值为10,最小值为-10。在Matlab软件中运行算法求解得到13组企业不同产能约束下模型M1和M*求解的近似最优订单接受策略。 企业基于时序关联性制定的订单接受决策是充分考虑订单长期发展潜在收益进行的决策,但是对当前的订单接受率、各项收益和产能利用率会产生一定的影响,笔者将对各指标因素进行对比分析。 3.2.1 订单接受率的比较 13组不同产能约束下的订单接受率(即选择接受的订单数量占所收到总订单数目的比例)与产能约束关系对比结果如表2所示。两种决策模型订单接受率对比如图3所示。其中,s1、s*分别为模型M1和M*的近似最优订单决策所选中的订单数量,γ1、γ*分别为模型M1和M*的订单接受率,ratio1为模型M1和M*的订单接受率差额占模型M1订单接受率的百分比,即ratio1=(γ*-γ1)/γ1×100%。 表2 模型M1和M*的订单接受率与产能约束关系对比结果 图3 两种决策模型所得订单接受率 由表2可知,考虑不同计划期内订单之间时序关联性的订单接受决策不会造成企业订单接受率大幅下降。当产能小于12 000时,企业产能无法满足订单的总需求,企业只能选择接受部分订单,此时模型M*的订单接受率略低于模型M1,但差异并不大,在数量上最多仅相差一个订单的数量。当产能大于12 000时,模型M1和M*的决策结果几乎没有差异。所以在不同产能约束情况下,相较于M1决策情形下的订单接受率,M*的决策情形下的订单接受率仅小幅下降。 3.2.2 产能利用率的比较 13组不同产能约束下的决策结果得到的实际产能利用率(即决策结果中实际消耗的企业产能与企业总产能约束的比值)数据如表 3所示,两种决策模型产能利用率对比如图4所示。其中,δ1、δ*分别为模型M1和M*的近似最优订单决策在当前计划期内的产能利用率,ratio2为模型M1和M*的产能利用率差额占模型M1订单产能利用率的百分比,即ratio2=(δ*-δ1)/δ1×100%。 表3 模型M1和M*的产能利用率 图4 两种决策模型所得产能利用率 由表 3可知,在不同产能约束下,模型M1和M*的产能利用率没有明显差距,这种差距远小于1%,所以考虑时序关联性不会对订单接受决策之后订单的产能利用率造成很大的影响,在保证订单的产能利用率没有大幅下降的同时实现企业长期利润最大化。 3.2.3 各种收益的比较 表4 模型M1和M*的当前总收益 表5 模型M1和M*的未来期望引致总收益 表6 模型M1和M*的期望总收益 图5 两种决策模型所得各项收益 由表4~表6可知,与模型M1相比,模型M*的订单当前总收益较低,但是其未来期望引致总收益和期望总收益均较高,并且在企业有限产能较低时,模型M*的未来期望引致总收益和期望总收益比模型M1更高,当企业产能较充足时,两种情形下的收益差距变小。相比于模型M1,模型M*的当前总收益的减少幅度远小于期望总收益的增幅,因为模型M*在决策时舍弃少量当前收益来换取未来更高的收益,有效避免企业短视决策,实现企业长期利益的最大化。 综上所述,在企业产能约束情况下,考虑时序关联性的订单接受决策可以使企业的订单接受率和产能利用率保持较高水平的同时实现企业长期收益最大化,更加符合企业的长期发展目标。 3.2.4 鲁棒性分析 订单数量为30个,企业产能约束为16 000时,将算法运行500次,分别求解模型M1和M*所得结果如表7所示。 表7 算法分别求解模型M1和M*运行500次的结果 由表7可知,改进粒子群算法在求解决策模型时能够有效得到最优解。算法运行500次,考虑时序关联性的订单接受决策模型,求解的最优解为577 451,最差解为561 728,两者之间相差不大,并且达到最优解的概率为93%,说明该算法求解模型结果具有较好的鲁棒性。 通过设置不同的订单规模进行订单接受决策模拟仿真来验证改进粒子群算法的有效性和稳定性。以考虑时序关联性的订单接受决策模型为例,最大产能设置为16 000,其他参数与前文保持一致,改变订单规模,分别将基础粒子群算法和改进粒子群算法针对每种情形进行仿真实验,结果如表8所示。 由表8可知,不论订单规模大小,改进粒子群算法所得最优解均高于基础粒子群算法,并且改进粒子群算法的收敛速度较快。改进粒子群算法降低了陷入局部最优的概率,提高了全局寻优能力,引入的差分进化策略可以有效提高种群多样性,寻优效率跟基础粒子群算法相比有了较好的改善。 表8 模型M1和M*的期望总收益 为进一步分析两种算法的稳定程度、收敛速度等因素,将基础粒子群算法和改进粒子群算法分别针对模型M1和M*独立运行500次,绘制目标函数值(适应度值)曲线、迭代次数曲线、运行时间曲线,如图6~图9所示。由图6~图9可知,改进粒子群算法所得目标函数值的平均值比基础粒子群算法更优,且目标函数值和运行时间更加稳定。 图6 改进粒子群算法求解模型M1所得结果 图7 改进粒子群算法求解模型M*所得结果 图8 基础粒子群算法求解模型M1所得结果 图9 基础粒子群算法求解模型M*所得结果 通过建立考虑时序关联性的定制订单接受决策模型,采用改进粒子群算法对模型进行求解,并且以全屋定制企业为例进行实证分析,得到以下结论: (1)当前计划期内的订单可能在未来时间窗口内以一定概率引致订单需求,所以企业在进行订单接受决策时不能片面地只考虑订单的当前收益,还需要考虑订单的未来潜在收益。 (2)根据全屋定制的个性化定制订单生产加工特点,建立考虑订单之间存在时序关联性的订单接受决策模型。通过实证分析可得,在产能有限的情况下,考虑订单之间的时序关联性可以使订单接受率和产能利用率保持较高水平的同时实现企业的长期利润最大化,有利于企业的长期发展。 (3)改进粒子群算法对于求解订单接受决策模型有很好的鲁棒性和有效性,可以有效解决企业个性化全屋定制订单长期利润优化导向的接受决策问题。但是笔者仅考虑了企业的产能约束,对于订单的交货期约束没有开展深入的研究,未来可以考虑订单在不同交货期约束的情形对模型进行改进和研究。3 实证分析
3.1 案例背景与订单数据

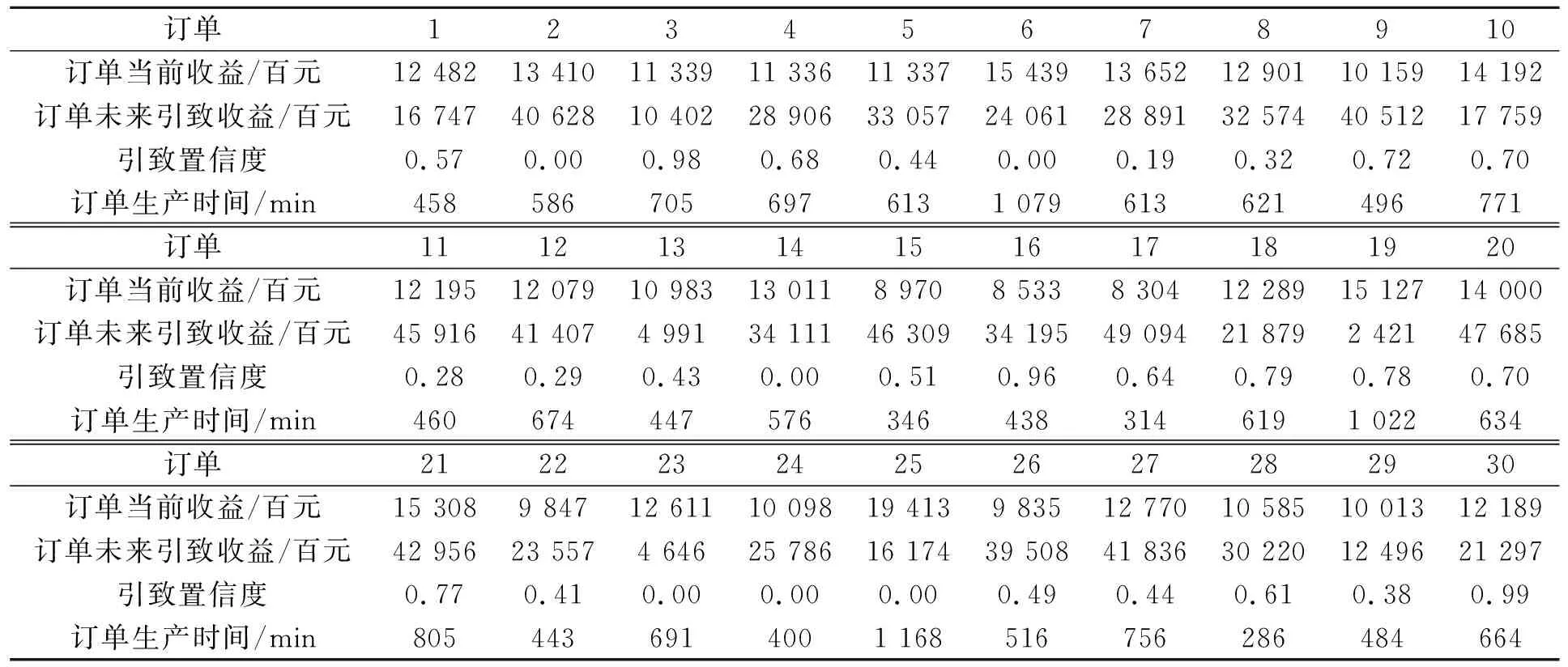
3.2 考虑订单具有时序关联性对订单接受决策的影响分析
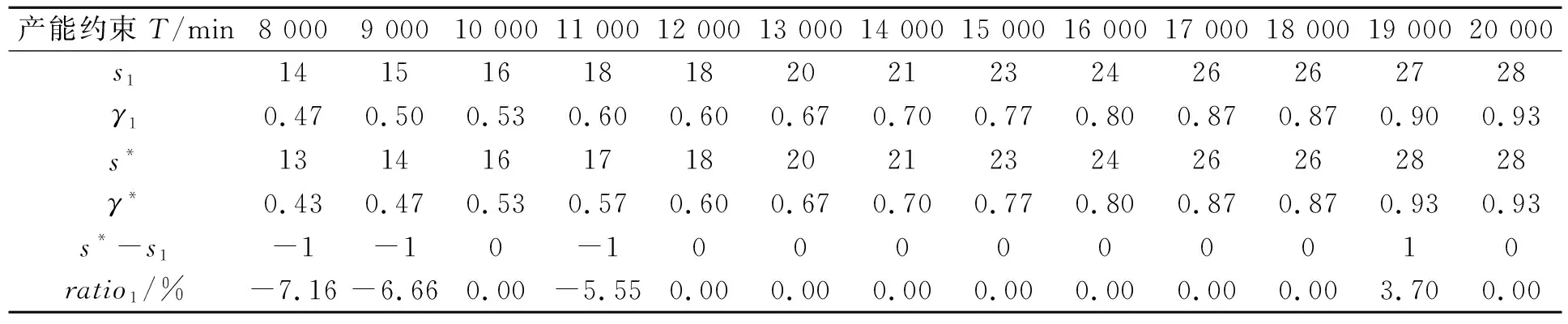
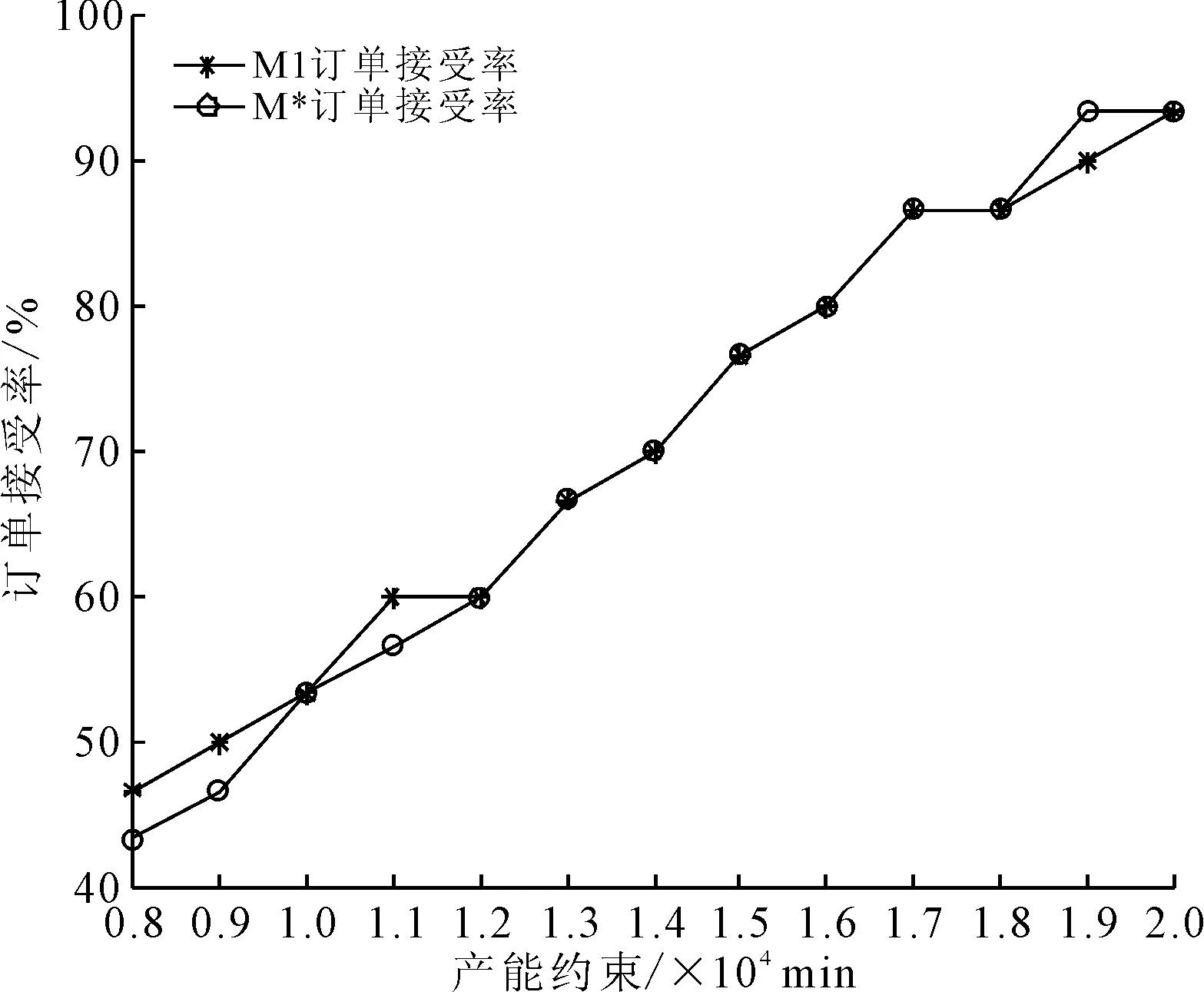

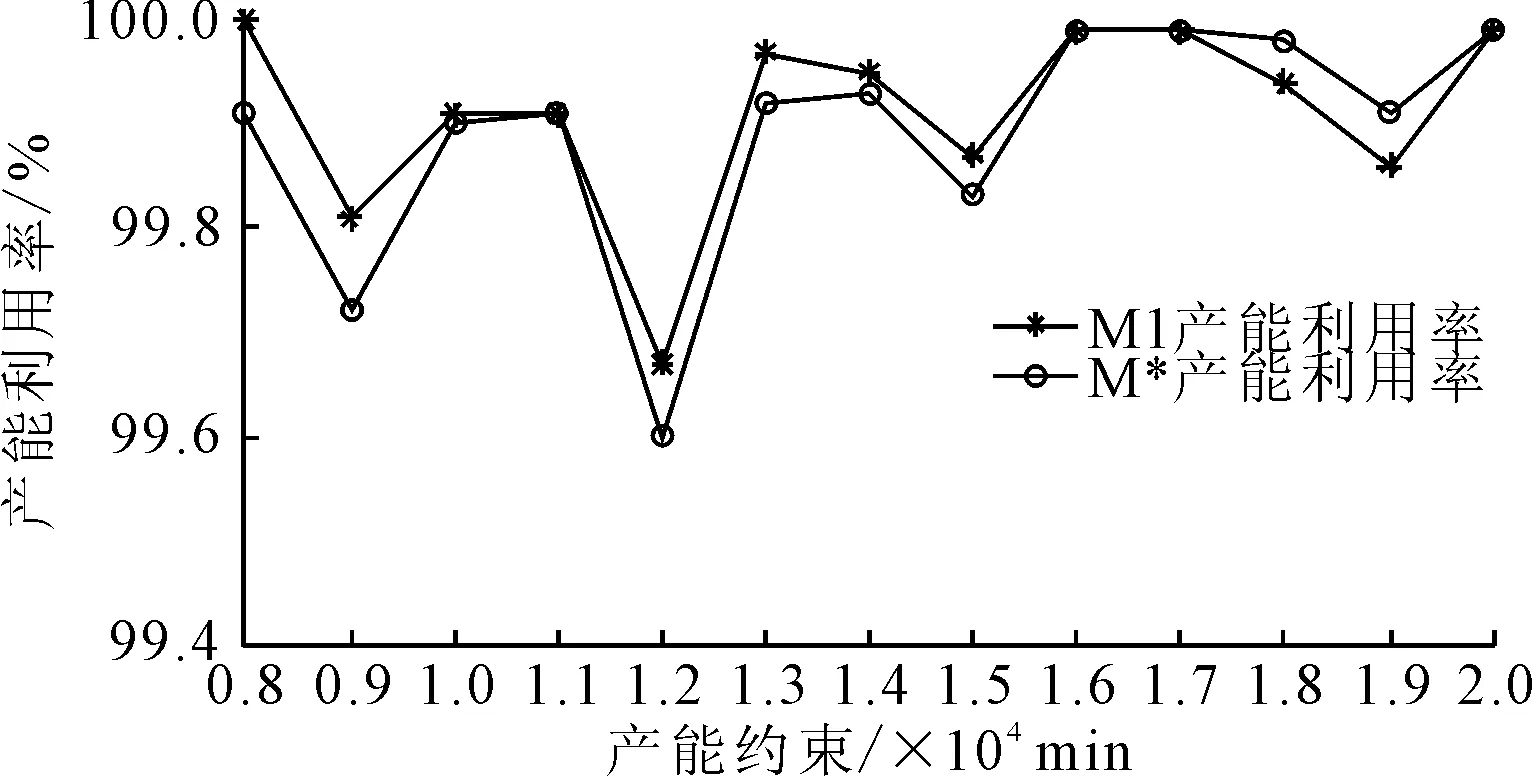
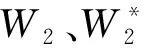



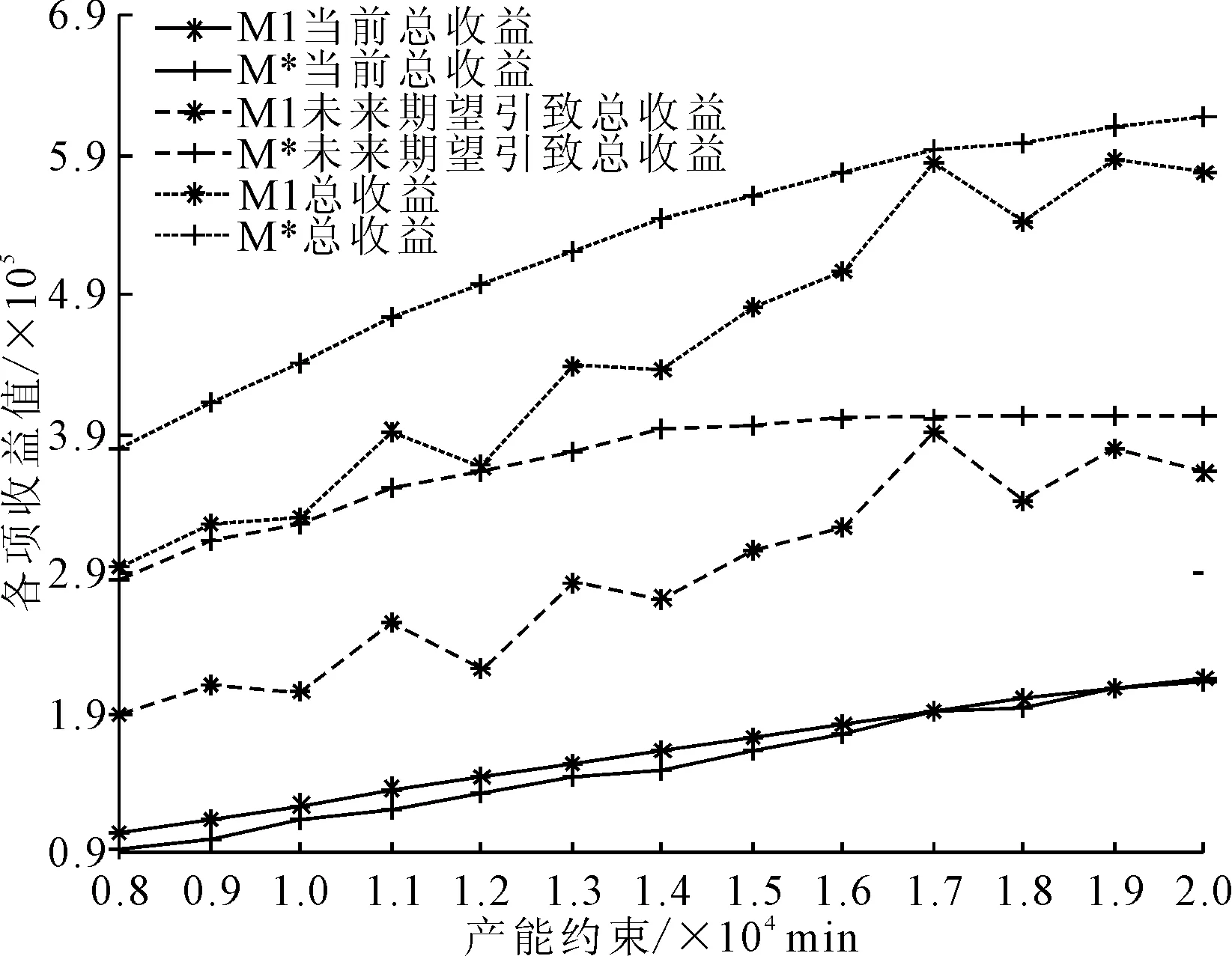

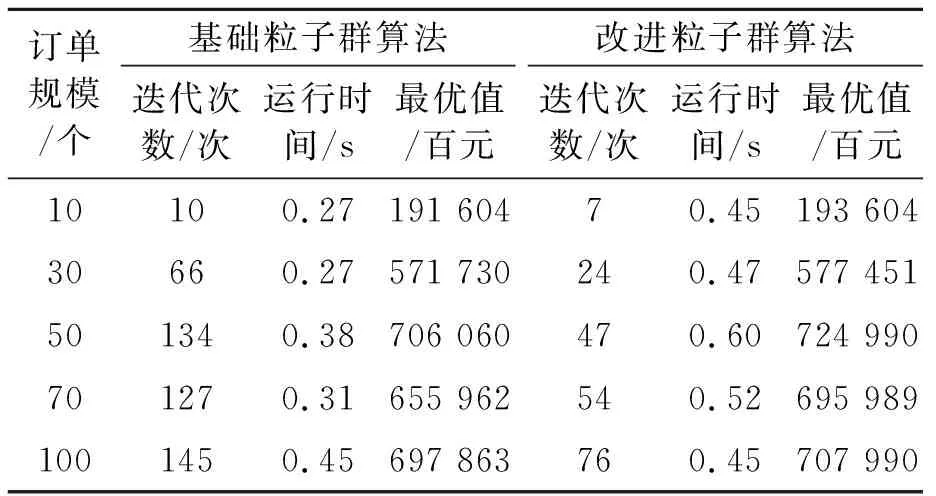
3.3 不同算法的比较分析
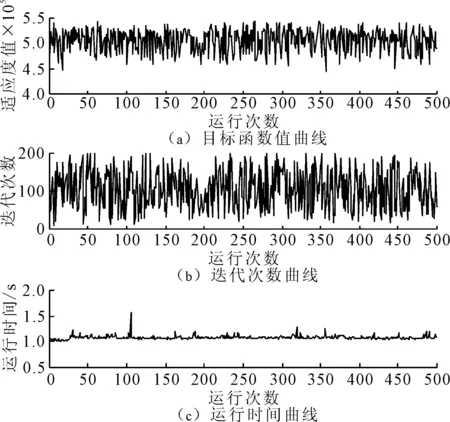
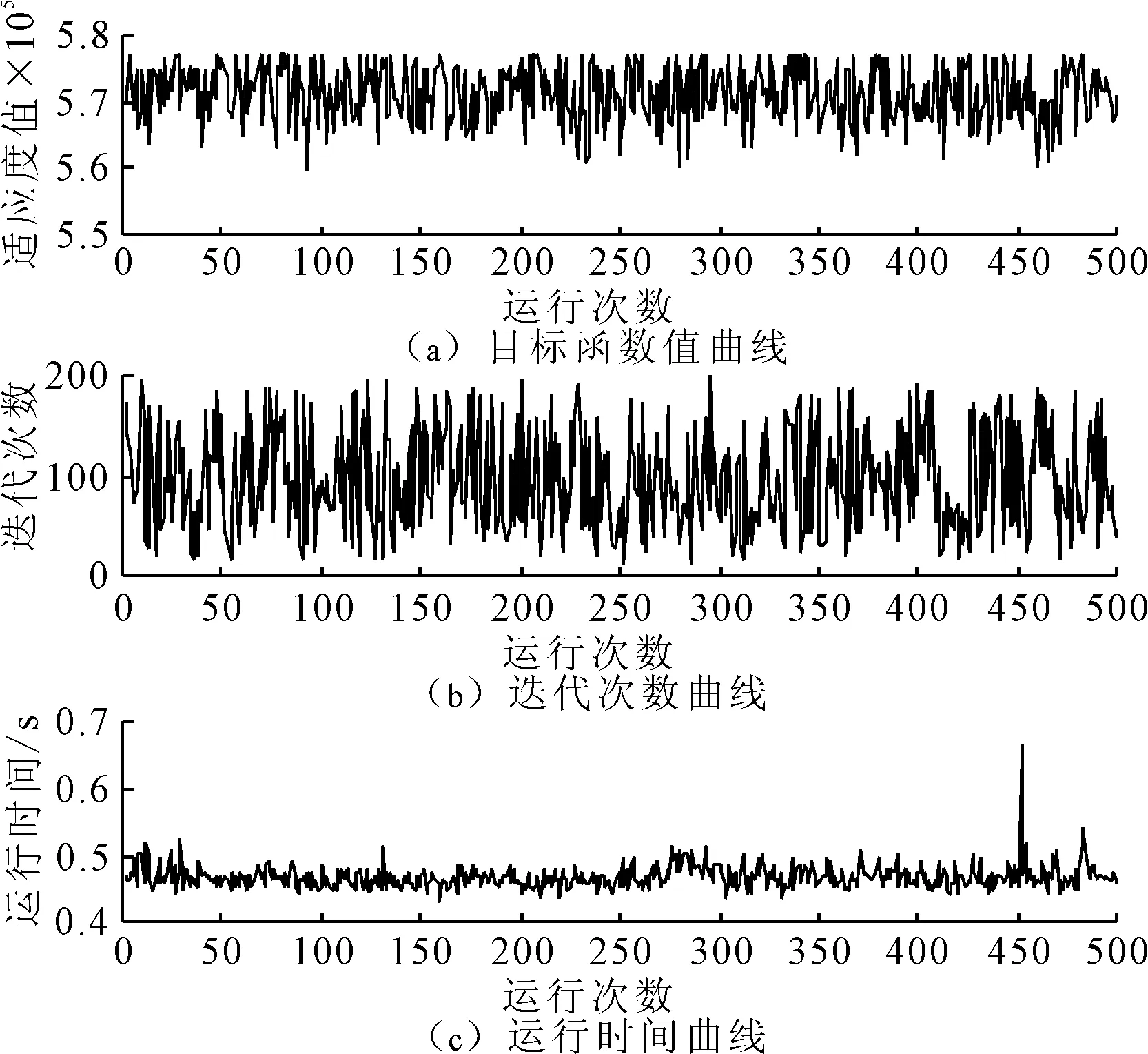
4 结论

