轨道交通对沿线房地产价格的影响分析

刘芳聪，李鹏博，田丽君

(福州大学 经济与管理学院，福建 福州 350116)

随着城镇化进程的不断加快，城市边界不断扩张，城市规模不断扩大，城市人口剧增，交通出行拥堵成为了城市居民日常生活的一大难题。城市轨道交通以其容量大、准时、高效、安全、舒适等优点成为提高出行质量和缓解交通拥挤的有效出行工具。

城市轨道交通在缓解交通拥挤，提高出行舒适度的同时，由于沿线区域可达性的提高而影响居民的住宅选址，进而影响区域内房地产价格。BRANDT等[1]通过对地铁可达性范围内的周边房价进行分析，最终算出距站点一定范围内的住宅收益金额可以达到2.33亿欧元(折合人民币约17.18亿元)，而且能获得4 200万欧元(折合人民币约3.21亿元)额外税收。刘康等[2]基于特征价格方法构建计量分析模型，实证分析了南京市地铁1、2号线对沿线站点住房价格的影响,结果表明城市轨道交通对沿线站点住房价格产生了显著的增值效应，不同距离范围影响程度不同。耿化祺等[3]基于特征价格模型，对乌鲁木齐市轨道交通1号线沿线2 000 m范围内二手住宅小区价格增值效益进行实证分析，结果表明住宅小区距最近站点的距离与住宅价格成反比，且对住宅价格影响最为明显，带来的增值效益为7.08%。于宁等[4]基于广义交通费用的出行选择模型对福州市地铁周围房地产增值情况进行预测，计算结果显示轨道交通运营后沿线各站点会有187.75元/m2到2 439.37元/m2不等的增值。张维阳等[5]构造衰减模型分析房价与距地铁站距离的相关关系，发现北京地铁1号线站点对住宅价格的影响范围从0.5 km到1 km不等，衰减比重为20%～35%，且在影响范围内衰减程度逐渐降低。田丽君等[6]通过建立消费者剩余模型和居住地Logit选择模型预测轨道交通建设对居住区位选择与住宅价格的影响，结果表明随着轨道交通沿线居住区位可达性的提升，轨道交通附近房价增长，最远的居住区位平均增长2 619元/m2，最近的居住区位平均增长11.5元/m2。BOWES等[7]通过特征价格模型分析轨道交通带来的通勤成本降低和吸引零售业两种积极因素，以及噪音污染和增加犯罪率两种消极因素，对区域内房地产价格的影响，发现这4种因素均对房地产价格有显著影响。综上，国内外学者大多利用特征价格模型，该研究方法一般基于大量的房地产交易数据及详细的周边信息，虽然考虑的影响因素较为全面，但多因素可能会导致寻找大量实际的房产交易数据较为困难，且各因素之间的交互作用及因素的主观选取可能使结果产生一定的偏差。另外，城市的差异性可能会导致凭经验确定研究的影响范围不合理。

基于此，为量化轨道交通对沿线房价的增值效益，从而为实现轨道交通的开发利益还原政策提供理论基础，笔者通过住宅区位理论，建立基于个人出行的房地产增值预测模型，以南昌市地铁1号线为研究对象，对轨道交通建设后沿线房价的增值效益及其规律进行分析。

1 模型构建

假设房地产相关政策平稳，区域发展因素稳定。基于Alonso住宅区位理论，考虑出行者在交通出行成本与购房成本之间进行权衡，追求总成本最低，最终达到市场均衡状态，然后通过广义交通成本模型以及考虑资金时间价值的收益还原，建立轨道交通对沿线房地产的效益预测模型。

1.1 住宅区位理论模型

住宅区位理论最早是由温哥和阿朗索(Alonso)提出来的，从交通出行费用和住房费用的角度出发，研究两者的相互影响。模型假设城市只有1个CBD中心，交通系统以相同的效率运送所有出行者到城市中心工作，房屋类型相同，且不考虑房屋结构、地形特点等因素的影响；居民的消费支出仅由住房支出、交通出行费用和其他消费支出组成[8-9]，简化的数学模型为：

Y=O+P(x)·G+K(x)

(1)

式中：Y为家庭的可支配收入；O为其他消费品支出；P(x)为距离城市中心x处的住宅房价；G为该家庭的住房面积；K(x)为距离城市中心x处的广义交通费用。

1.2 增值预测模型

假定轨道交通建设运营前后家庭可支配收入Y、其他消费支出O、家庭住房面积G保持不变，当轨道交通建设运营后，各出行者会在购房成本和上升的交通出行费用之间进行权衡，最终达到市场均衡状态，即居民住房消费差与交通成本差相等[10]：

ΔP(x)=P1(x)-P0(x)=

(2)

式中：P0(x)、P1(x)分别表示轨道交通运营前后距市中心x处的沿线房地产价格；ΔP(x)为距离市中心x处轨道交通运营前后的房价差；K0(x)，K1(x)分别表示轨道交通运营前后的广义交通费用；ΔK(x)为距离城市中心x处轨道交通运营前后的广义交通费用差。

另外，由于居民购房时是一次性支付费用，而出行费用的差异是由每天的出行活动累计而成的。因此，在考虑资金时间价值的情况下，假定每年的收益率不变，根据收益还原法可以将式(2)修正为[11]：

(3)

式中：γ为收益还原率；n为房屋的使用年限(一般为70年)。由式(3)可知，轨道交通沿线房价增值的大小取决于广义交通费用差值，因此有必要考虑出行者的出行方式选择，进而对出行费用差值进行分析。

1.3 广义交通费用模型

广义交通费用是指出行者在出行过程中所支付的快捷性、可靠性、经济性、舒适性等服务属性方面的成本。为简单起见，只考虑经济性成本(票价或燃油费)、快捷性成本(出行时间成本)和拥挤成本(出行方式的舒适度成本)。由此，距离城市中心x处的居民采用不同出行方式至市中心的广义交通费用Ci(x)为：

Ci(x)=Fi(x)+α·Ti(x)+Mi

(4)

式中：i=1、2、3、4分别对应公交出行、自驾出行、步行接驳地铁和骑单车接驳地铁4种出行方式；Fi(x)为距离城市中心x处居民采用第i种出行方式至市中心的经济性成本，即票价或燃油费，对于自驾出行，此项还包括停车费用；α为出行者的单位时间价值；Ti(x)为距离城市中心x处居民采用第i种出行方式到市中心所需的时间，包括车内时间、接驳时间和候车时间3部分；Mi为拥挤成本，为方便处理，这里取常数，舒适度的基础值取各种运输方式票价或燃油费的5%(平峰期)到10%(高峰期)[12]。其中，出行时间可表示为：

Ti(x)=Ti0(x)+Ti1(x)+Ti2(x)

(5)

式中：Ti0(x)为距离城市中心x处居民到市中心所需的车内时间，即从出发站点到市中心的车内时间；Ti1(x)为距市中心x处居民在站点的候车时间，对于乘地铁出行，还包括进出站点的时间，对于自驾出行，此项为0；Ti2(x)为距市中心x处居民到附近站点的接驳时间，对于公交出行，还包括终点站至目的地的步行时间，对于自驾出行，此项为0，对于乘地铁出行，此项是指采用接驳方式(步行或骑共享单车)至起点站的时间和终点站至目的地的时间。由此可得，距市中心x处居民至市中心的年广义出行费用为：

K(x)=365·f·Ci(x)

(6)

其中，f为居民家庭一天的出行频率。

1.4 基于个人出行选择的增值预测模型

地铁建成运营前后，出行者会根据不同出行方式的出行成本进行权衡选择。因此，将出行成本作为负效用，根据Logit模型，居民选择不同出行方式的概率可以表示为：

(7)

式中：Pi(x)为距离城市中心x处居民到市中心选择第i种出行方式的概率；θ为一个固定的常数，θ越小，表示出行者的出行选择越随机，这里取θ=0.5；Ci(x)表示距离城市中心x处居民到市中心选择第i种出行方式的广义交通费用；J为居民可选择的交通方式集合。

为消除指数级增长导致的结果差异严重扩大，对式(7)进行均值化处理，则可以得到改进后的各出行方式的选择概率：

(8)

在地铁建成运营之前，居民选择公交出行的概率可以表示为：

P1(x)=

(9)

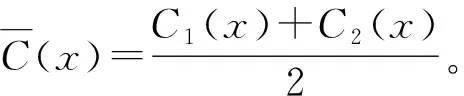
因此，可以得到地铁建成运营前，距离城市中心x处的居民至市中心的出行费用为：

C0(x)=P1(x)·C1(x)+(1-P1(x))·C2(x)

(10)

在地铁建成运营后，出行者根据各出行方式的出行费用权衡选择，选择概率分别为：

(11)

(12)

(13)

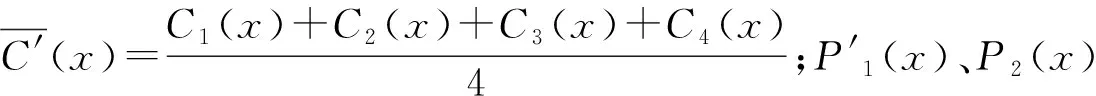
P2(x)-P3(x))·C4(x)

(14)

那么，将地铁的分担率代入后便可计算出一年内广义交通费用差为：

ΔK(x)=365·f·(C0(x)-C(x))

(15)

2 实证分析

以南昌地铁1号线站点为对象，分析地铁建设前后沿线房地产价格的变化情况。由于南昌地铁1号线与2号线在地铁大厦站至八一广场站存在交叉影响，因此选择1号线双港站至卫东站的部分站点进行计算分析。

2.1 基础数据

研究涉及的基础数据分为直接数据和其他数据，直接数据主要包括模型中各项基础数据，由南昌统计局统计数据及南昌市统计年鉴得到。为方便计算，笔者考虑出行者每日通勤出行量为2次，按照每个家庭3个人计算，因此可取家庭每日出行频率f为6次/天。根据南昌市2019年国民经济和社会发展统计公报数据可知，城镇居民人均住房面积为38.94 m2，按家庭规模为3人计算，取G为116.82 m2。房地产价格在政策平稳、发展稳定的背景下虽有一定的波动，但幅度不大，因此γ取中等风险下的收益还原率10%[13]。根据南昌市统计局发布的统计年鉴显示，非私营单位年人均工资为72 686元，按照劳动和社会保障局提供的小时工资折算方法，取α为34.81元/h。另外，取公交票价为2元；地铁票价根据不同的起始站点取为2～6元，可由南昌地铁官方网站查询具体票价；共享单车骑行费用取1.5元/次；自驾出行的燃油费一般为0.6元/km，停车费可取8元/次。由于出行者以通勤为主，即乘车一般在高峰期，因此M可取票价的10%。

其他数据主要是指车内时间、候车时间和接驳时间。对于公共交通，通过出行距离与运行速度来衡量车内时间会导致结果存在较大误差，加上南昌1号线已处于正式运营阶段，相关的时间数据也较容易获取，因此笔者直接通过相关交通工具的时刻表与百度地图进行测算，得到地铁乘车与公交乘车的车内时间。至于自驾出行，车内时间则是通过出行距离和自驾车时速进行计算，自驾通勤的平均车速可取35 km/h。

由于南昌市不同区域的公交线路规划与发车安排不同，因此公交等待时间不完全相同，一般为3～8 min，可根据具体区域的具体线路进行取值。南昌轨道交通1号线高峰期的发车间隔为10 min，因此可取地铁乘车的平均候车时间为5 min，乘地铁进出站时间为3 min。

接驳时间主要考虑两种接驳方式到地铁站的时间，正常出行者的平均步行速度V1一般为5 km/h，骑自行车的平均速度V2一般为10 km/h，笔者考虑不同接驳距离下轨道交通建设运营前后对房价的影响程度，接驳距离由百度地图测距得到。

2.2 房地产增值预测结果及分析

笔者选取地铁大厦为市中心，对南昌地铁1号线的部分站点进行分析。同时，由于距地铁站的距离不仅会影响出行者的接驳方式，还会影响房价的增值程度，因此选取的计算距离分别为站点附近小区、站点周围步行接驳边界、站点周围骑自行车接驳边界。

2.2.1 站点附近小区

地铁建设运营前后附近居民单次出行成本分别如表1和表2所示，地铁运营所带来的家庭年出行成本的降低值及房价的增加值如表3所示，可知各站点房价有153.52～998.40元/m2不等的增值。从表中计算的数据可以看出，距离市中心越远，家庭单次出行成本越高。同时，由地铁的建设运营所带来的出行成本的减少值越大，房价的涨幅也越高。

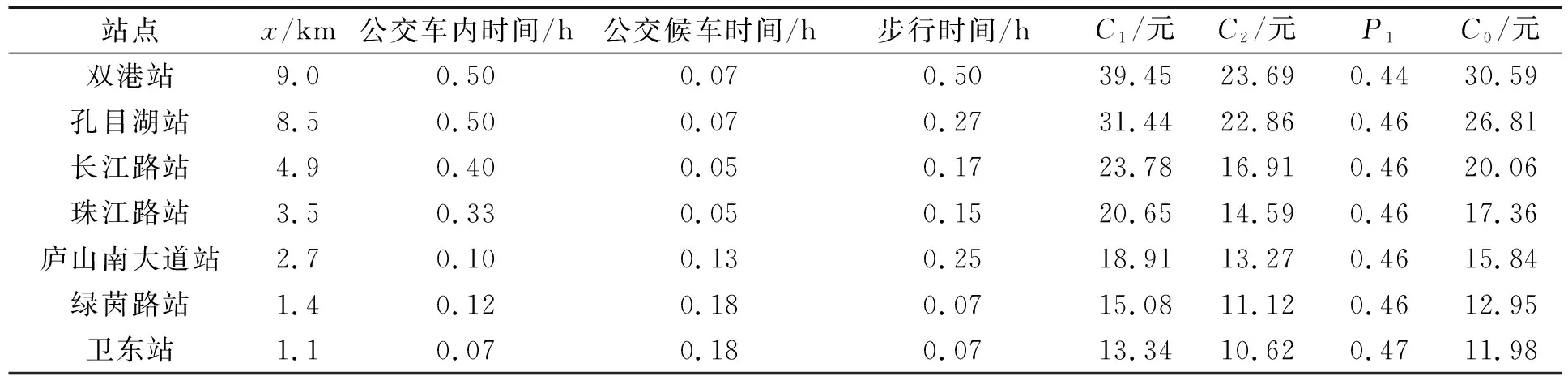
表1 地铁建设运营前站点附近居民单次出行成本

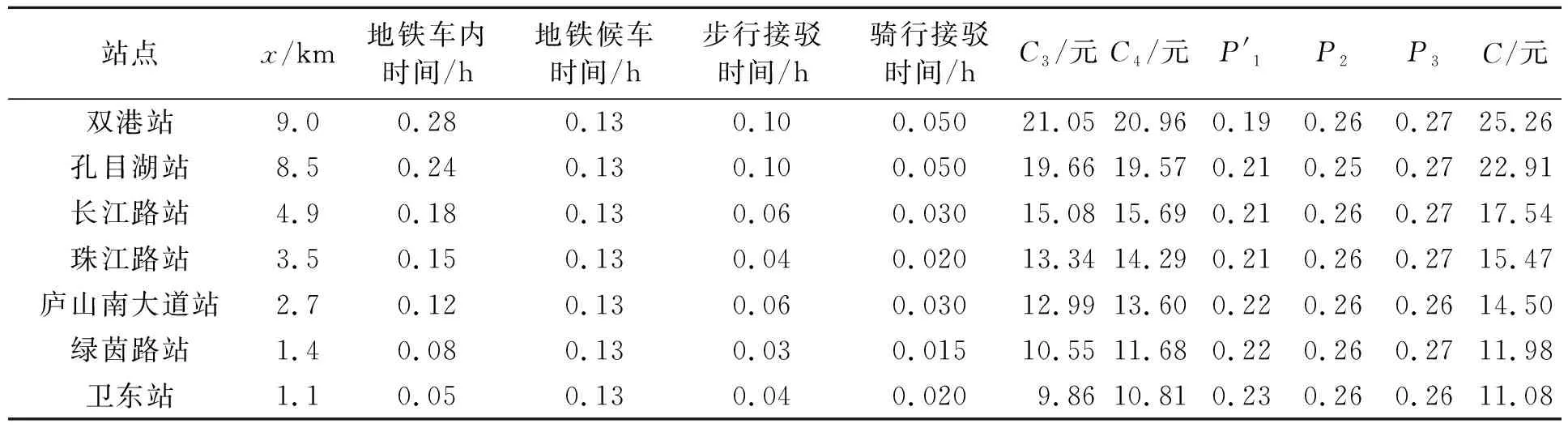
表2 地铁建设运营后站点附近居民单次出行成本

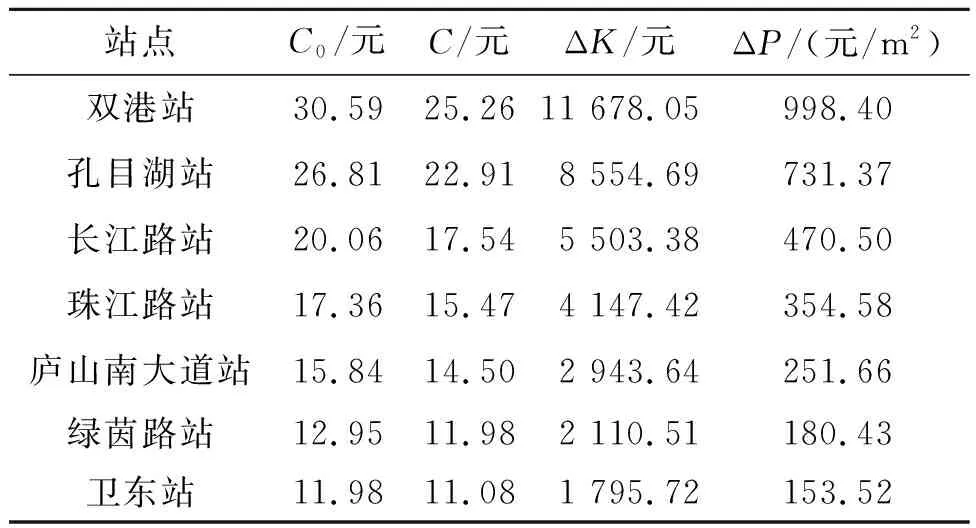
表3 站点附近居民家庭年出行成本

2.2.2 站点周围步行接驳边界

基于地铁各站点附近出行者的出行成本数据，利用地铁建设后步行和骑行接驳地铁至市中心的出行成本与原出行成本相等，从而计算出步行接驳边界R1和骑行接驳边界值R2。R1、R2的计算方式分别如式(16)和式(17)所示，各地铁站点影响边界值的计算结果如表4所示。

(16)

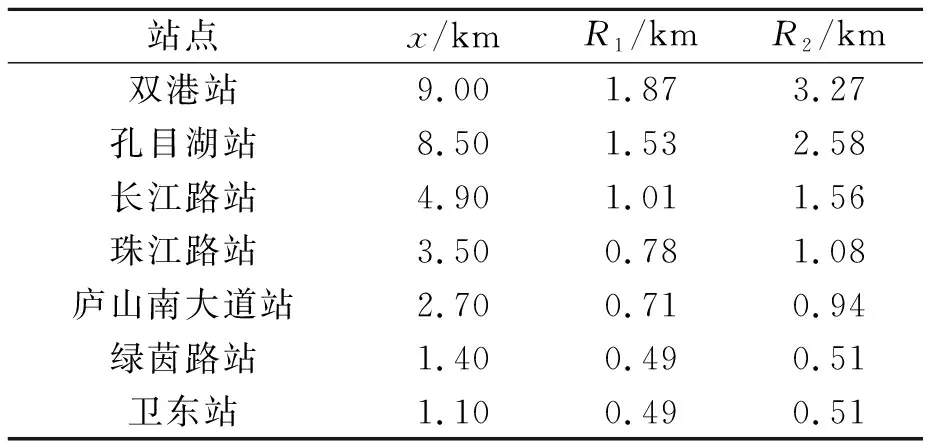
表4 地铁站点接驳方式的影响边界值

(17)

式中：F3为站点步行接驳边界处至市中心的地铁乘车费用；T30为站点步行接驳边界处至市中心的车内时间；T31为站点步行接驳边界处至市中心的候车时间；V1为步行平均速度；F4为站点骑行接驳边界处至市中心的地铁乘车费用；T40为站点骑行接驳边界处至市中心的车内时间；T41为站点骑行接驳边界处至市中心的候车时间；V2为骑行平均速度。

地铁建设运营前后，在步行接驳边界处以家庭出行的角度计算单次广义交通费用计算值，分别如表5和表6所示。地铁建设运营所带来的家庭年出行成本的降低值与房价的增加值如表7所示，可知各站点房价有97.57～292.07元/m2不等的增值。同样地，地铁建设运营所带来的出行成本的减少值不全相等，在距市中心中等距离处的长江路站增值幅度最大，且沿长江路站至市中心增值幅度逐渐降低；而在孔目湖站出现的山谷，是由于地铁票价的增加导致。

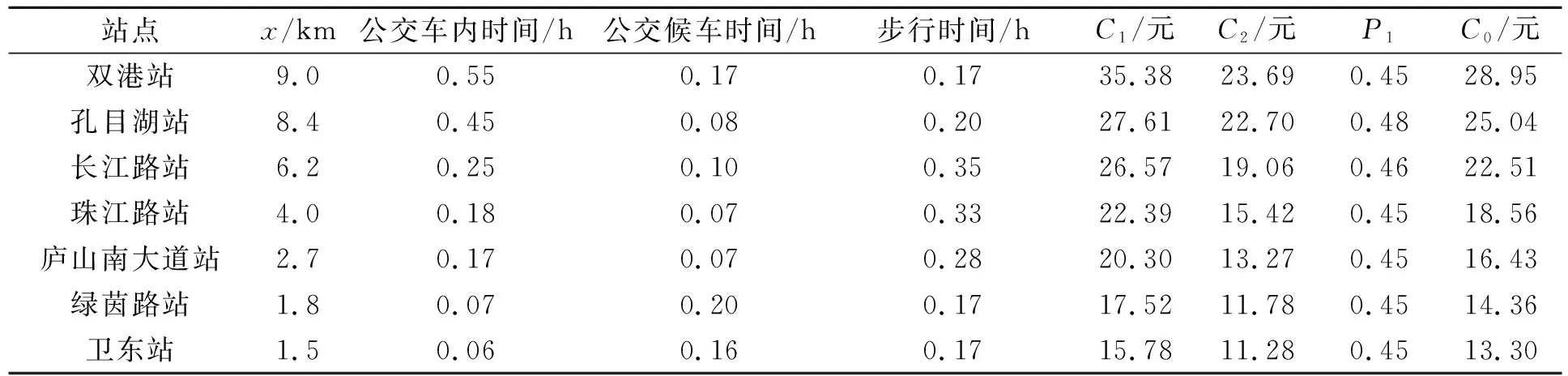
表5 地铁车站建设前步行接驳边界处家庭单次出行成本

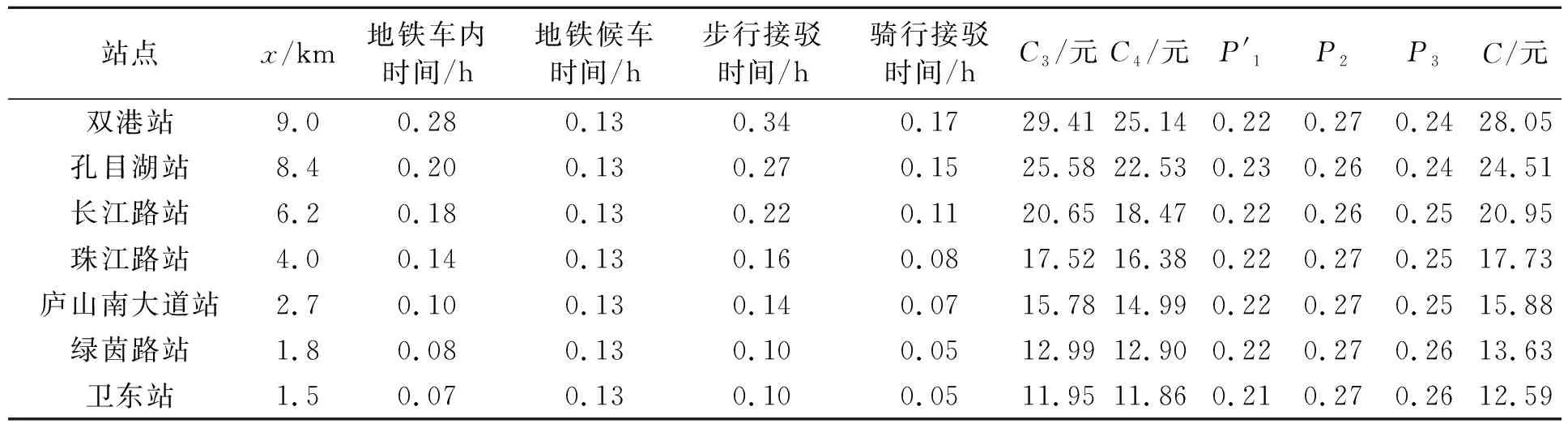
表6 地铁车站建设后步行接驳边界处家庭单次出行成本

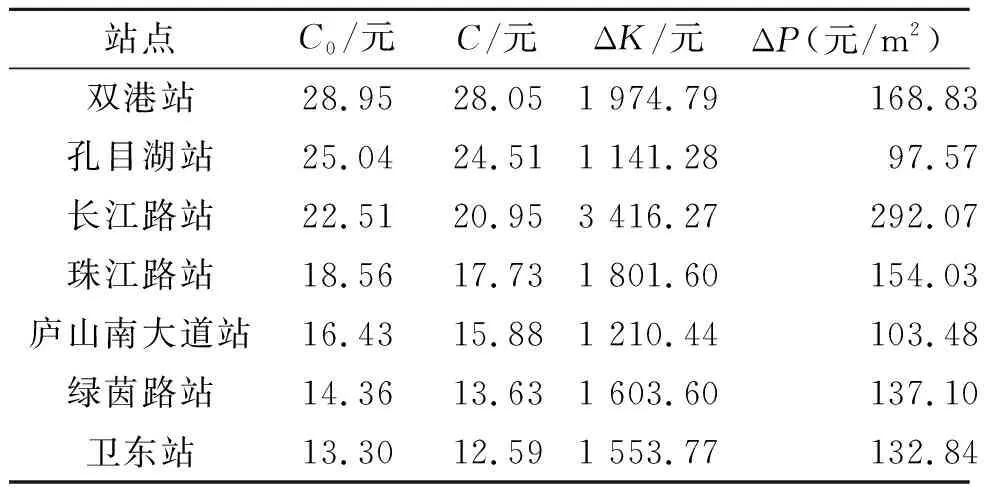
表7 步行接驳边界处家庭年出行成本

2.2.3 站点周围骑行接驳边界

地铁建设运营前后，以家庭出行的角度计算单次广义交通费用计算值,分别如表8和表9所示。地铁建设运营所带来的家庭年出行成本的降低值与房价的增加值如表10所示，可知各站点房价有5.69～128.83元/m2不等的增值。同样地，地铁建设前后出行成本的减少值表现为双港站处最大，沿双港站至市中心呈减小趋势，至庐山南大道站最小，这反映出在距地铁站点较远处和距市中心中短距离处的影响值最小，而距市中心距离最远处的站点的影响值最大。

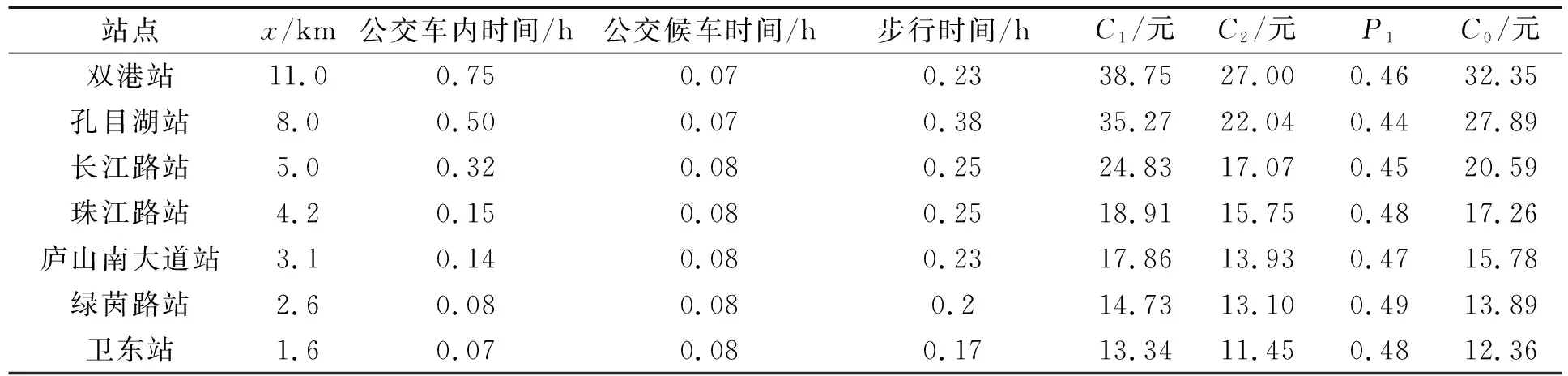
表8 地铁建设运营前骑行接驳边界处家庭单次出行成本

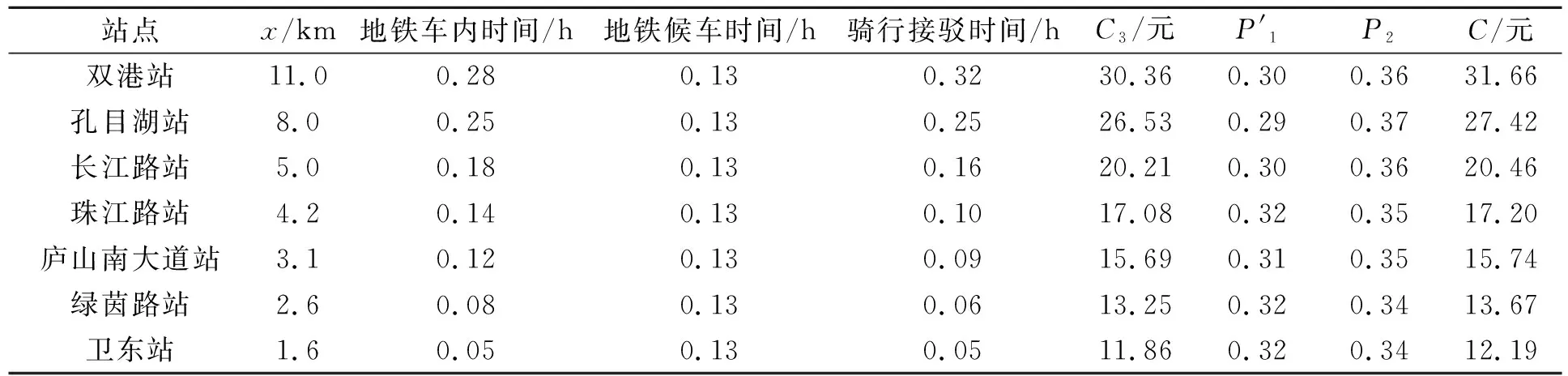
表9 地铁建设运营后骑行接驳边界处家庭单次出行成本

2.2.4 综合分析

将上述结果进行整理分析，得到不同距离对应的房价增长情况，如表11所示。由表11可知，相比于站点附近小区的出行成本与房价的变化值，步行接驳处的变化值明显降低，骑行接驳边界处的变化值进一步降低，但是出行成本的减少值与房价的增加值均为正值，验证了边界值计算的合理性。由此可见，轨道交通沿线房价增长的上界和下界都在随距站点距离的增加而减小。此外，横向距离(与站点的距离)对于房价的变化程度影响较大，且距市中心距离越远，横向距离带来的差值越大；纵向距离(距市中心的距离)对房价的变化相对较缓，且在距站点中等距离处，房价变化峰值会向市中心移动，而在站点较近和较远距离处，郊区的增值优势更明显。

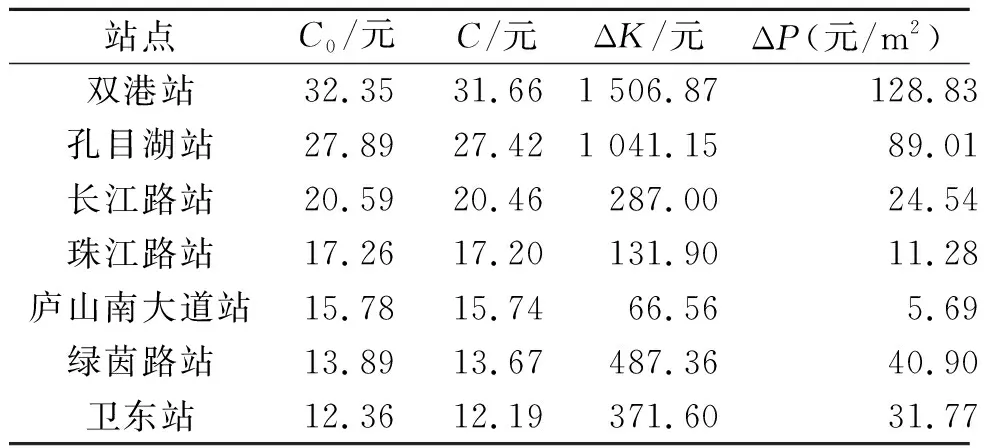
表10 骑行接驳边界处家庭年出行成本

表11 不同距离对应的房价增长情况

综合来看，在站点附近区域的结果与文献[3]和文献[4]得出的增值规律大致相同，但由于城市的差异性，房价的增值结果并不相同。

2.3 敏感性分析

2.3.1 理性程度的敏感性分析

为了反映居民基于出行成本考虑的理性程度参数对各站点区域平均房价增长的影响，以站点附近小区为分析对象，通过改变不同的理性参数取值，进而得到各个站点附近小区的出行成本与房价的平均增长值，如图1所示。由图1可以看出，在理性程度取0.5时，房价平均增长值最大。

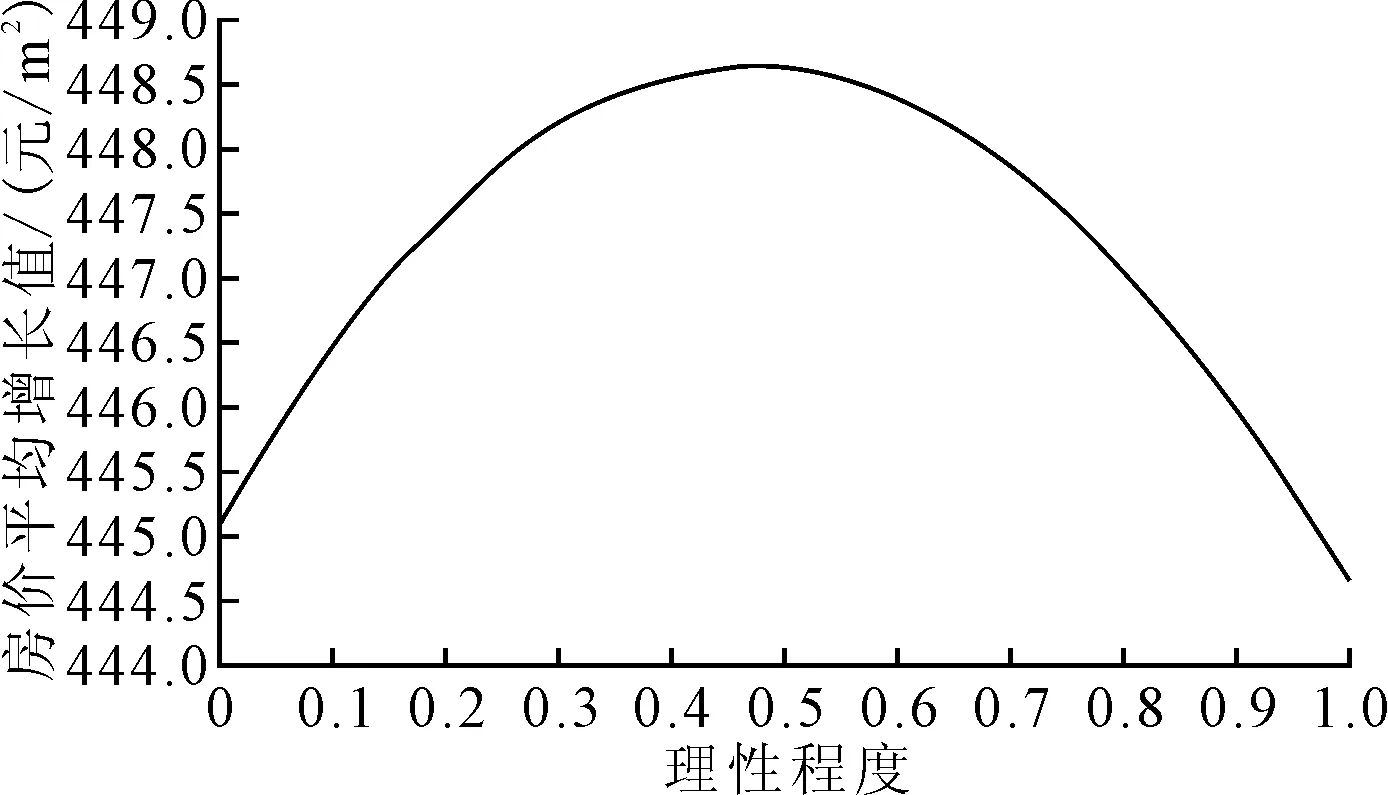
图1 理性程度的敏感性分析

2.3.2 距离的敏感性分析

固定理性程度为0.5，同样以站点附近小区为研究对象，计算不同距离下的出行成本数据与平均房价增长值，如图2所示。对所得数据进行线性预测，计算结果表现为距市中心距离每增加1 km，7个站点附近小区房价平均增长95.43 元/m2。

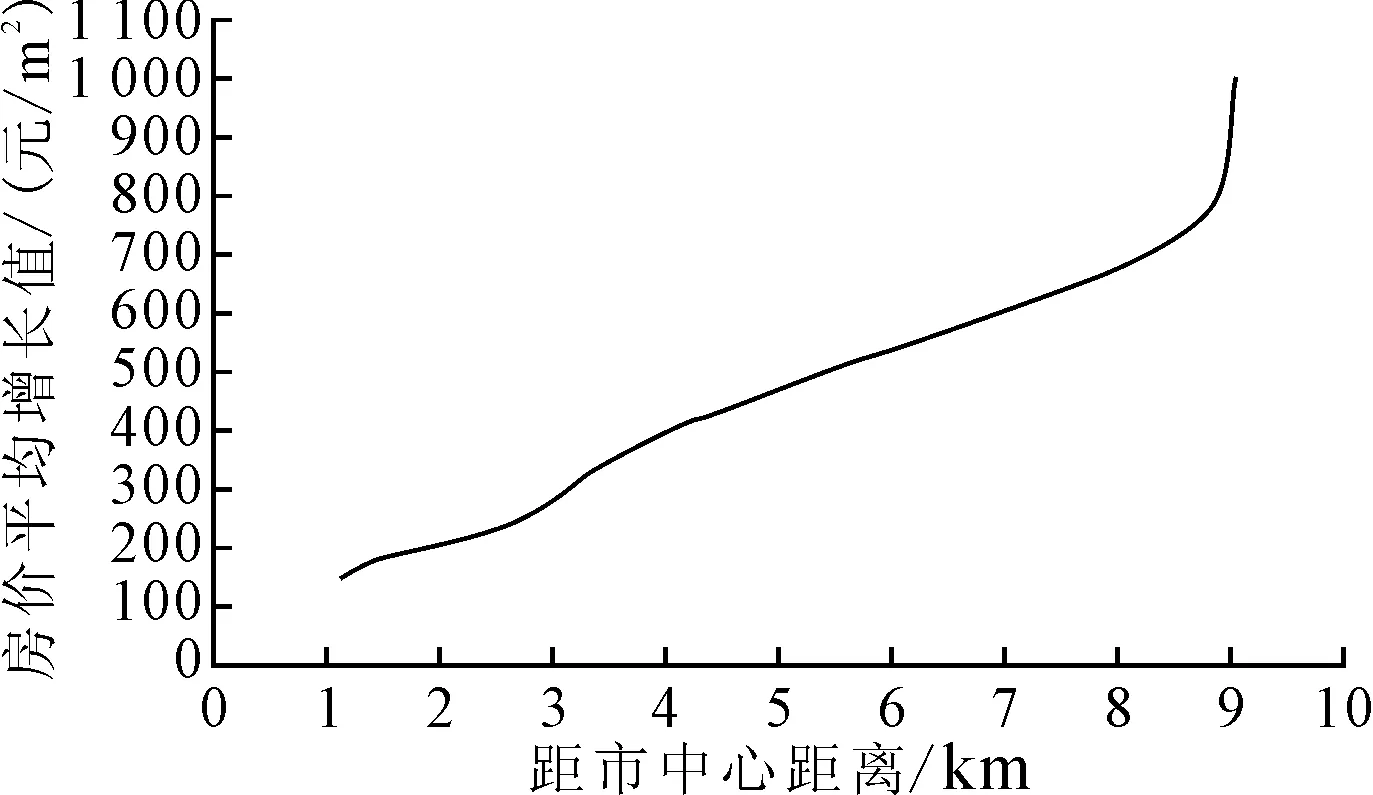
图2 距离的敏感性分析

2.3.3 地铁发车频率的敏感性分析

固定理性程度为0.5，公交票价为正常票价2元，通过改变地铁候车时间，得到不同的出行成本值，进而得到平均房价的增长值，结果如图3所示。具体计算结果表现为候车时间每增加0.01 h，7个站点附近小区平均房价增长36.14 元/m2。

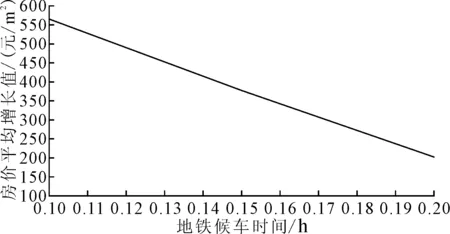
图3 地铁发车频率的敏感性分析

3 结论

(1)通过引入多元化的交通出行方式，同时在广义交通费用的计算过程中考虑个人基于成本的出行选择偏好；引入由成本表示负效用的Logit模型，在广义交通费用中考虑经济性成本(票价或燃油费)、快捷性成本(出行时间成本)和拥挤成本(出行方式的舒适度成本)。在此基础上，根据Alonso住宅区位理论建立了轨道交通对沿线站点区域房地产增值预测模型，对南昌市轨道交通1号线沿线站点周围房地产的增值情况进行了数值预测。

(2)无论是步行接驳还是骑行接驳，轨道交通站点的影响范围都表现为距市中心距离越远，站点的影响范围越大，两种接驳方式的影响范围差值也越大。

(3)交通出行成本表现为距市中心越远，广义出行费用越高，在骑行接驳范围内轨道交通对沿线房地产均产生增值效应，且在距站点较近(即步行接驳边界处)时，增值效应表现为“出现两处谷底的W型”，在距站点越远时(即骑行接驳边界处)，整体增值效益降低，各站点的增值规律表现为“V型”。

(4)轨道交通建设运营所导致的房价增长值并非表现为“距市中心距离越远、房价增长值越大”的线性增长规律。同时，在距站点中等距离处，房价变化峰值会向市中心移动，而在站点较近和较远距离处，郊区的增值优势更明显。

(5)由于笔者只选取了站点周围3个距离值进行分析，因此无法准确描述各个站点周围房价与距站点距离的变化关系，同时在考虑接驳方式与出行方式时，只选取了主要的交通方式，在个人出行选择分析中，只考虑成本对出行者的影响，可能会与实际值存在一定的偏差。