基于实测数据的地下通道行人疏散运动规律

刘 轩，李海冰，房志明

(1.广东省建筑科学研究院集团股份有限公司 建筑消防研究所，广东 广州 510500；2.广东省建设工程质量安全检测总站有限公司，广东 广州 510500；3.上海理工大学 管理学院，上海 200093)

地下通道作为一种有效的辅助通行结构，被广泛应用在地下综合体、地铁换乘和主干道路口等。相比于普通通道，地下通道往往空间有限、更易聚集密集人群，需要辅助照明，但是紧急情况照明条件有限。一旦地下通道的人群中发生摔倒、火灾、异响等突发扰动情况，极易引起人群慌乱、拥挤推搡，踩踏事故发生的可能性也大大增加。例如，2010年7月24日，德国西部鲁尔区杜伊斯堡市举行“爱的大游行”电子音乐狂欢节时，通向活动现场的一个地下通道里发生踩踏事件，造成21人死亡、342人受伤。因此，研究分析地下通道内人群运动行为规律，是保障地下通道人群流通安全及应急疏散安全的基础，具有重要的现实意义。

使用实际观测方式采集人群运动过程资料进行分析是研究人群运动行为规律的典型方法，如HELBING等[1]对麦加朝圣中的大规模人群录像资料进行了图像处理和理论分析，发现密集人群的运动会自发地出现由“自由流”到“走走停停波”，再到“湍流运动”的相变。当人群处于“湍流运动”状态时，内部压力突然释放会使行人跌倒，进而引发踩踏事故。刘立元等[2]选取地铁车站的通道设施为研究对象，通过视频采集、后期人工处理得到行人流运动特征参数的数据资料，并拟合出通道设施内行人流交通特征参数之间的理论关系曲线。张文辉等[3]以福州铁路北站为研究对象，对枢纽内部的行人流数据进行视频采集，对行人流参数数据进行筛选和拟合分析，建立了不同设施的行人流参数关系曲线及函数模型，发现水平通道处行人流流量与密度呈二次函数关系，流量与空间在某一临界点两侧分别呈二次函数关系和对数函数关系，速度与密度呈线性关系。杨丽丽[4]结合北京西直门综合枢纽的行人流调查数据，分析了枢纽内不同步行设施上的行人自由速度分布特性，采用单因素方差分析法对影响因素进行分析。贾洪飞等[5]通过实地观测水平通道内部，研究流量、密度、速度三者之间的关系，构建模型分析了行人最小静态空间、动态空间。孙惠芳[6]在广州地铁车站观测人群运动数据，统计性别、年龄、负重、结伴、使用手机和高跟鞋6个因素对城市轨道交通车站通道内行人交通微观特征参数的影响，并从乘客属性、心理特征、行为特征、设施环境、其他行人影响等方面分析统计结果的产生原因。周继彪[7]以西安市北大街地铁站为例，对枢纽内行人交通特性进行了深入研究，结果表明行人步行的平均速度为1.114 m/s；行人密度与速度拟合关系符合线性函数形式，行人速度随着密度的增大而减小；行人密度与流量拟合关系符合一元三次方函数形式，行人流量随着密度的增大先增大后减小。李俊梅等[8]开展了居民楼有烟环境中人员沿楼梯上行移动特性的研究，指出烟气环境中心理作用是影响移动速度的重要因素。

在行人交通研究方面，很多学者[9-13]对行人交通特性等进行了大量调查，包括但不限于行人交通流基本特征参数、行人交通流速度特性、行人交通流流量特性、行人交通流参数关系、行人交通流延误特性和行人过街安全心理距离分析。刘旭光等[14]开展了多组上下楼疏散实验，对疏散效率、速度、密度、流量等典型特征进行了分析，结果表明人员微观疏散行为与楼梯结构有着紧密的联系，在楼梯出入口和阶梯段更容易出现拥堵。孟琦[15]在城轨车站中研究了站厅场景下可视距离、从众程度和初始密度与平均疏散时间等疏散特性的关系。马云龙等[16]基于观测数据分析了基本步行路段的行人特性，指出少年儿童、青年、中年和老年人的步速、步幅和步频平均值的差异均较显著。黄利华等[17]研究了乘客在地铁突发事件下对典型疏散行为的认知情况，指出大多数乘客缺乏应急疏散经验和演练经历，其中疏散措施选择与乘客年龄、学历存在相关性。龚晓岚等[18]为了估计行人交通流的自由速度及其分布，在分析行人步行速度受约束概率的基础上，基于改进的Kaplan-Meier估计方法，对行人的自由速度估计方法进行了分析，用大量的实测数据建立了不同步行设施上行人的自由速度分布模型，发现行人的自由速度符合正态分布。

综上可知，现有研究针对地下通道的实测数据较少，故笔者选取某典型的地下通道开展观测实验，分析地下通道内的人群运动规律，以期为地下通道人群疏散仿真[19]及应急管理提供依据。

1 实测实验

1.1 实验设计

选取某地下通道为研究对象，如图1所示，该通道连接商圈和地铁站，客流密集，节假日更甚。该通道净宽度为8.74 m，高度约为2.2 m，客流双向通行。故笔者在某周六的高峰时段，使用手持摄像机对该通道的客流进行视频采样。

图1 某地下通道及测量区域示意图

1.2 参数提取

对摄像机记录的视频数据进行处理，分析实验中的详细运动参数和特殊现象。因为本次观测实验在地下通道开展，摄像机的布置位置受限，拍摄的画面角度达不到计算机图像自动处理的标准，所以采用人工方法处理本次实验的数据。主要关注通道内人群的运动参数，包括速度、密度、流量等，为了统计上述运动参数数据，选定图1矩形框标记的测量区域，该区域宽度W=8.74 m，长度L=5.23 m，人群沿长度方向运动，测量的参数与测量方法为：①运动时间(Δt)，即在采集的视频数据中跟踪个体经过测量区域的时间；②运动距离(ΔS)，假定个体在测量区域内直线行走，因此个体运动距离ΔS=5.23 m；③运动速度(v)，个体运动速度即为运动距离与运动时间比值，v=ΔS/Δt；④运动步频(H)，即在测量区域内个体单位时间内迈步次数；⑤人群流量(F)，在采集的视频数据中，跟踪单位时间内通过通道横截面位置单位宽度内的人员数量；⑥人群密度(d)，在采集的视频数据中，计数每一时刻(每秒)测量区域内的人数N，则每一时刻测量区域内的人群密度为人数与测量区域面积的比值，d=N/(W×L)。

实验共跟踪了824位个体运动，针对每个个体，根据观测判断其属性信息，包括性别(男或女)、年纪(青年或中老年)、是否结伴(2个及以上个体共同运动视为结伴，否则为未结伴)、是否携物(携带背包、行李、婴儿车等记为携物，否则为未携物)。

2 行人流通规律分析

2.1 行人流通运动参数分析

实验跟踪了824位个体样本，提取每个个体的速度参数，全部个体样本的速度分布情况如图2所示。由图2可知，在允许双向通行的地下通道内，个体间速度差异较明显，整体分布在0.7～2.7 m/s之间，符合正态分布规律，人群速度的平均值为1.481 4±0.378 5 m/s。

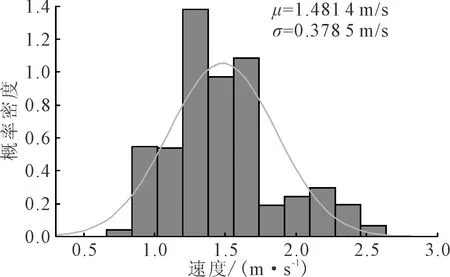
图2 人群速度分布图

因人群个体间速度差异明显，因此统计提取了824位个体样本的运动步频，全部样本的步频分布情况如图3所示，可以看出人群的步频分布范围为0.7～4.0步/s，说明在通道内个体运动的紧迫性差异明显。结合视频观察发现，有的个体目标明确，其步频较高，有的个体游玩为主，其步频较低。所有人群的步频符合正态分布规律，平均步频为1.836 4±0.490 2步/s。

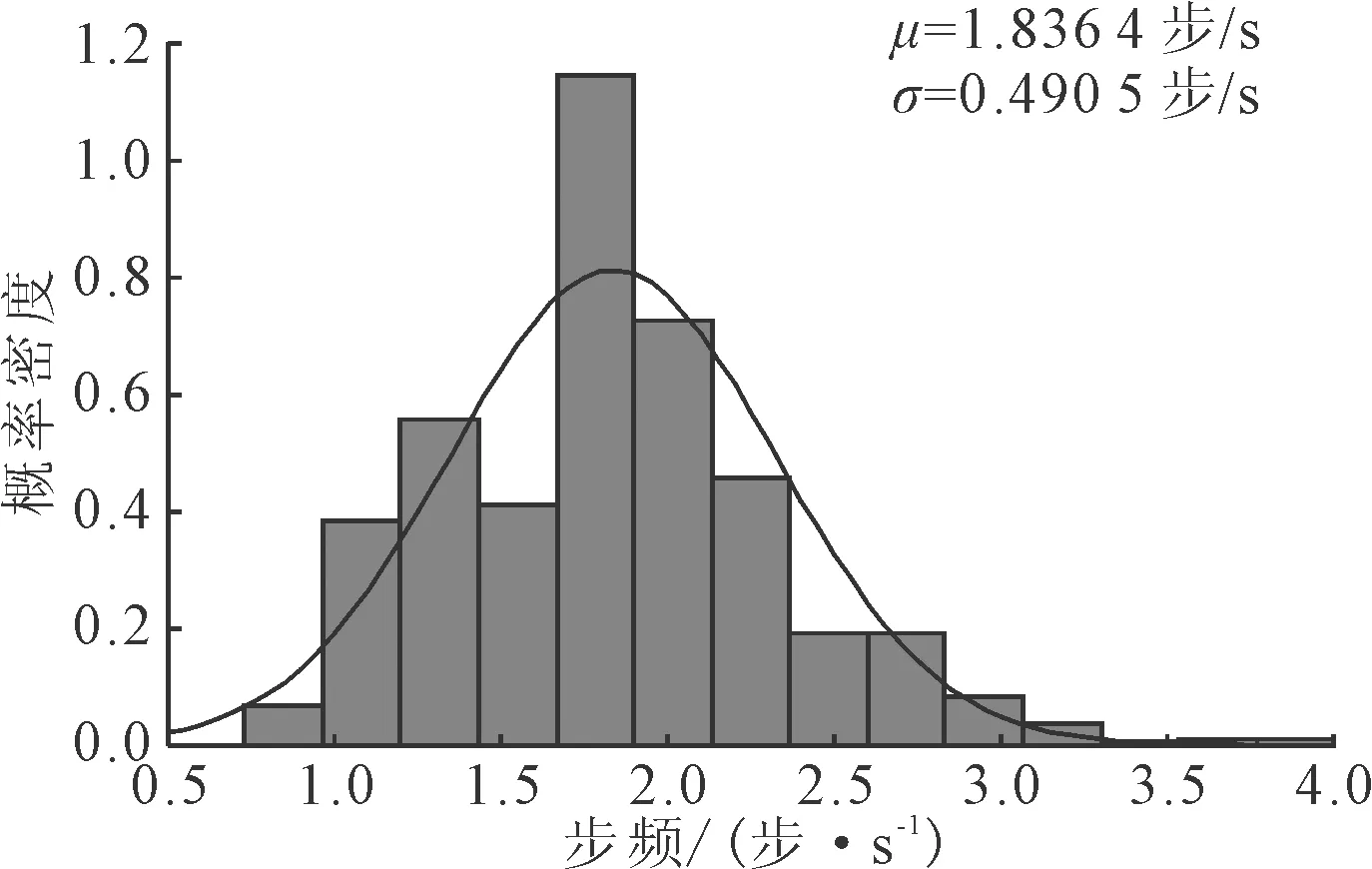
图3 人群步频分布图

密度-流量关系是决定人群运动效率的关键，美国国家消防协会(national fire protection Association)制定的美国消防工程师防火安全工程手册(the SFPE handbook of fire protection engineering)中给出的流量-密度关系为[20]：

F=1.4d-0.372 4d2

(1)

对于视频中的每秒时刻，提取了测量区域内人群密度-流量数据，如图4所示。由图4可知，随着测量区域内人群密度的增加，流量呈现明显上升趋势。而且，实测得到的密度-流量变化规律与手册给出的流量-密度关系一致，说明实验实测的运动参数结果具有代表性，能够表征地下通道内的人群运动规律。

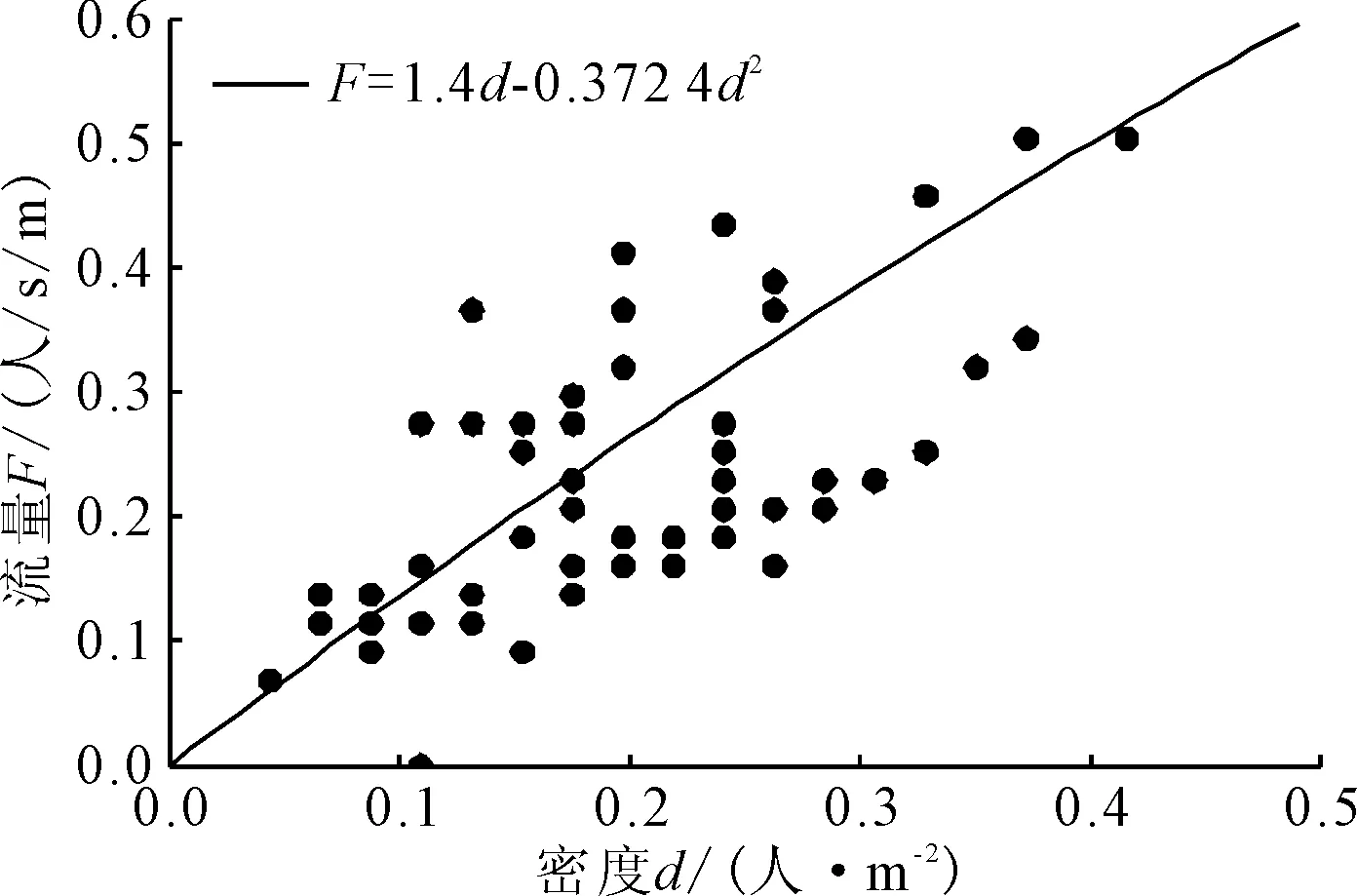
图4 人群密度-流量关系

2.2 行人流通影响条件分析

前文结果表明不同人群的速度差异与步频差异明显，为了进一步分析造成速度与步频差异的原因，将所有个体样本按照性别、年龄、是否携物、是否结伴进行分类，统计对比不同类别之间的速度与步频差异，并绘制了各类别速度与步频结果的箱型图与小提琴图。

不同类别人群的速度差异和速度差异的箱型图与小提琴图分别如表1和图5所示，可以发现：①824个样本中，男女各占一半，其中男性的速度为1.532 7±0.400 1 m/s，女性的速度为1.430 1±0.347 6 m/s，男性速度比女性高出7.18%。该项结果符合对不同性别人群运动能力的预期，即通常情况下男性运动能力强于女性，实验观测的人群是正常的普通人群，因此表现出男性的速度明显高于女性。②青年样本数量为403个，中老年样本数量为421个，其中青年速度为1.555 7±0.351 8 m/s，中老年速度为1.410 3±0.388 9 m/s，青年速度比中老年速度高10.31%。由于无法准确获取观测个体的年龄信息，只是根据观测个体的相貌特征主观判断其为青年人或中老年人。两类人群之间的速度差异也符合对不同年龄人群运动能力的预期，即通常情况下青年人运动能力强于中老年人。③携物人群样本量为384，不携物人群样本量为440，其中携物人群速度为1.463 8±0.402 1 m/s，不携物人群速度为1.496 7±0.356 3 m/s，不携物人群速度比携物人群速度高2.25%，说明携物在一定程度上会降低人群的运动速度。④结伴人群样本量为512，不结伴人群样本量为312，其中结伴人群速度为1.444 0±0.365 7m/s，不结伴人群速度为1.542 8±0.390 3 m/s，不结伴人群速度比结伴人群速度高6.85%，说明结伴在一定程度上会降低人群速度。

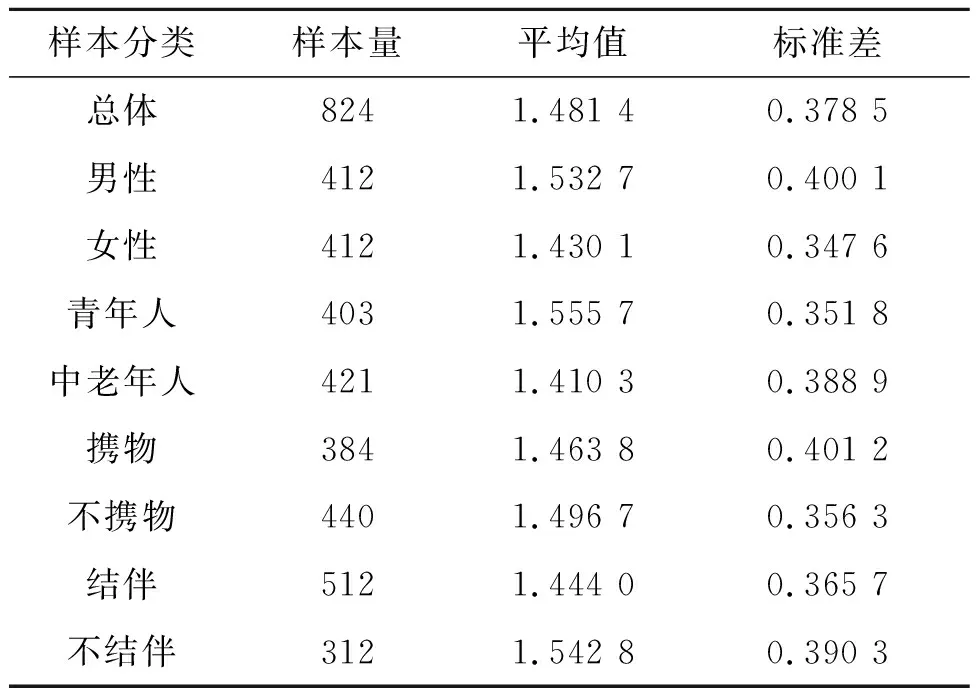
表1 速度差异统计分析结果

图5 不同类别人群速度差异的箱型图与小提琴图

不同类别人群的步频差异和步频差异的箱型图与小提琴图分别表2和图6所示，可以发现：①男性的步频为1.905 7±0.482 5 m/s，女性步频为1.767 1±0.487 5 m/s，男性步频比女性高7.84%；②青年步频为1.902 3±0.485 1 m/s，中老年步频为1.773 3±0.486 2 m/s，青年步频比中老年步频高7.27%；③携物人群步频为1.823 9±0.544 3 m/s，不携物人群步频为1.847 3±0.436 7 m/s，不携物人群步频比携物人群步频高1.28%；④结伴人群步频为1.810 5±0.475 2 m/s，不结伴人群步频为1.878 8±0.510 3 m/s，不结伴人群步频比结伴人群步频高3.77%。

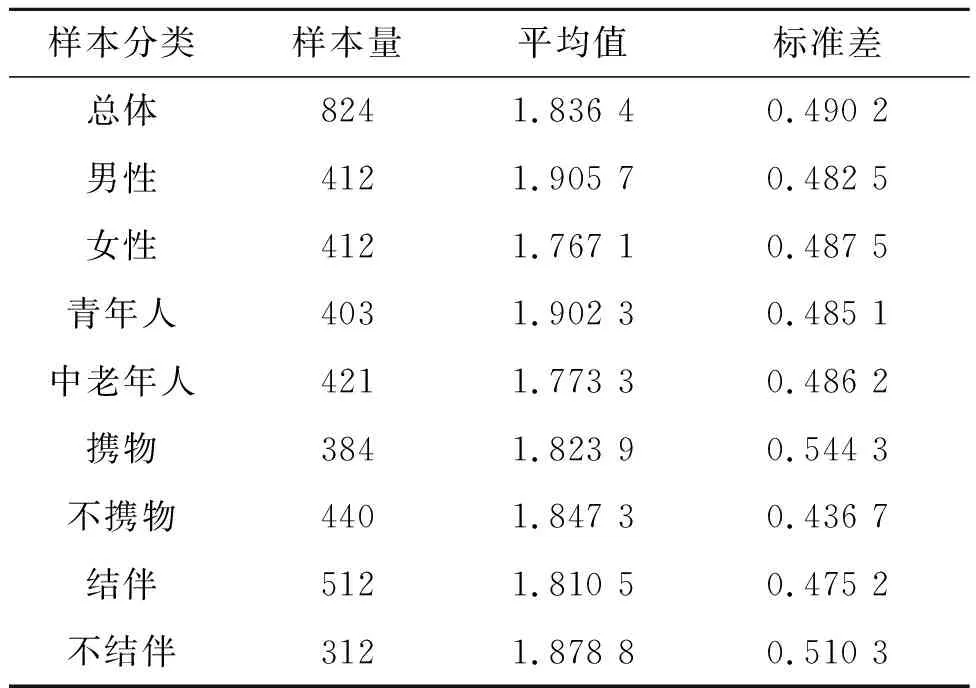
表2 步频差异统计分析结果

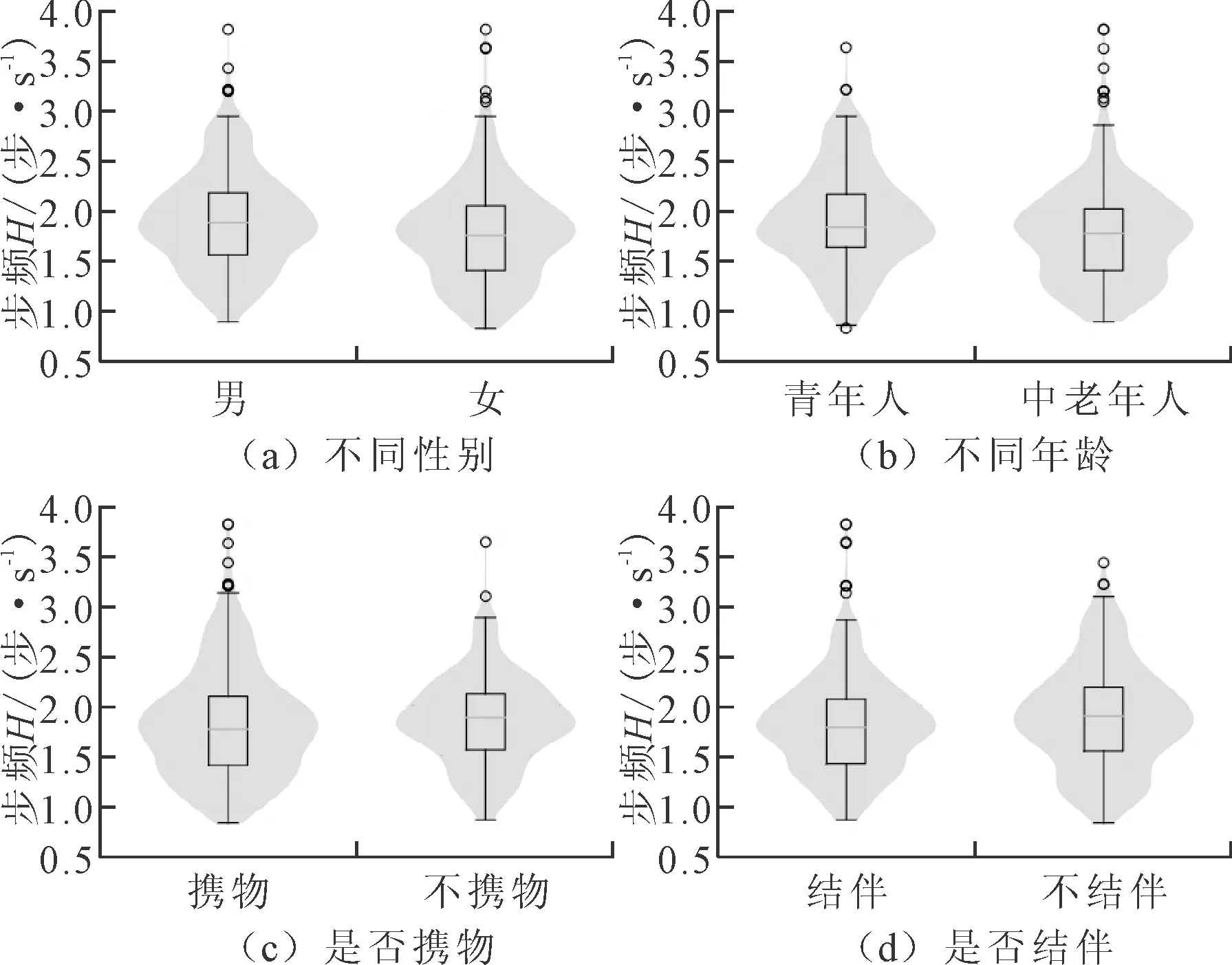
图6 不同类别人群步频差异的箱型图与小提琴图

笔者进一步采用SPSS软件对824个样本的性别、是否结伴、是否携物、年龄分组等属性信息及其运动速度与步频进行相关性分析，如表3所示。结果表明：①速度与步频之间呈现显著相关性，证明个体速度由其步频决定，个体步频越大，速度越大，再结合图2与图3说明个体紧迫性差异造成步频差异，进而表现出明显的速度差异；②性别与速度和步频呈显著相关性，说明性别密切影响通道内人群运动参数；③年龄与速度和步频呈显著相关性，说明年龄决定了人群运动参数；④是否结伴与速度呈显著相关性，与步频相关性不显著，说明结伴行为在一定程度上影响人群运动参数；⑤是否携物与速度和步频的相关性不显著，说明在商圈附近的地下通道内，人员携带的随身物品不足以影响其运动参数。

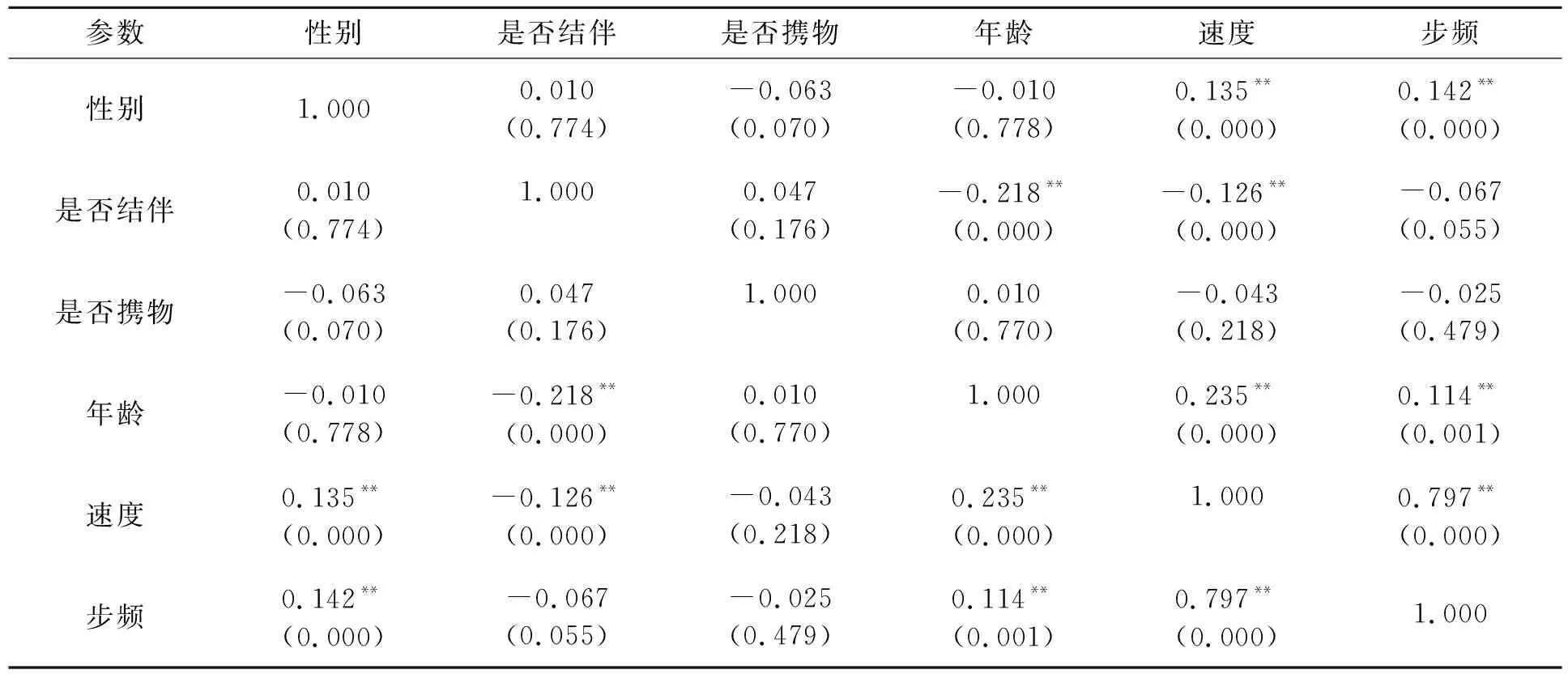
表3 人群运动参数与人群分组相关性分析

3 结论

(1)在某地下通道开展了人群运动观测实验，采集获取了824个行人样本数据，统计了人群速度、步频分布情况及密度-流量关系，并分析了不同类别人群下的运动参数差异。

(2)地下通道人群的速度为1.481 4±0.378 5 m/s，步频为1.836 4±0.490 2步/s，符合正态分布规律；实测得到的密度-流量变化规律与SFPE手册给出的流量-密度关系式一致，说明实验实测的运动参数结果具有代表性，能够表征地下通道内人群运动规律。

(3)地下通道内人群速度与步频之间呈显著相关性，个体速度由其步频决定，运动紧迫性差异造成步频差异，进而表现出速度差异；地下通道内性别、年龄与个体的速度、步频显著相关性，男性的速度、步频高于女性，青年人的速度、步频高于中老年人；根据平均值结果，地下通道内携物人群的速度、步频低于不携物人群，结伴人群的速度、步频低于不结伴人群。