累积Logistic回归模型结构变点的序贯检验

李拂晓, 肖燕婷, 陈占寿

(1.西安理工大学理学院, 陕西 西安 710054;2.青海师范大学数学与统计学院,青海 西宁 810008)

1.引言

分类变量在现实生活中十分常见, 如每个学生的期末考试成绩按分数段可分为“优秀”,“良好”, “及格”和“不及格”四类; 每个人的血压值可分为低血压, 正常和高血压三类.按照时间顺序记录分类变量值, 即构成分类时间序列.关于分类时间序列的建模, 研究者提出了多种模型, 如Markov链模型, 广义线性模型, 整数自回归模型和自回归滑动平均模型等.广义线性模型可以把响应变量的条件期望表示为过去观测值和协变量的函数, 且相比Markov链模型, 既不需要假设马氏性, 也不需要假设平稳性, 是分类时间序列建模比较常用的模型[1].累积Logistic回归模型(Cumulative logistic regression model)是一类重要的广义线性模型, 在生物医学, 社会科学和遗传学等领域有着广泛的应用.

在数据分析中，数据所服从的模型由于受到某些因素的影响, 可能在某个时刻或位置发生改变, 即产生变点.过去的几十年中，有许多学者研究了模型的结构变点检验和估计问题.[2-9]变点检验一般分为回顾性检验(Retrospective test)和序贯检验(Sequential test), 前者是分析已观测的历史数据, 检验数据中是否存在变点; 后者是连续检验数据中是否存在变点, 即新观测的数据是否仍符合原有的模型,也称为在线监测[10].针对回顾性变点检验,Antoch[11]基于整体最大值型(Overall maximum type)统计量研究了广义线性模型的结构变点检验问题.Hudecova[12]利用得分型统计量研究了二分类自回归模型(Binary autoregressive model)的结构变点检验问题.Fokianos[13]等基于偏似然得分过程构造统计量, 检验二分类Logistic回归模型的系数是否存在变点, Gombay[14]等将其推广到多分类Logistic回归模型.WANG等[15]在高维同质性检验的基:上提出了一种新的方法, 研究了具有大量类别的多分类数据的变点估计问题.关于变点的序贯检验, XIA等[16]分别基于残差的累计和(Cumulative sum, CUSUM)和滑动和(Moving sum, MOCUSM)构造统计量, 在线监测广义线性模型的结构是否存在变点.Hohle[17]利用CUSUM方法在线监测分类时间序列所服从的Logistic回归模型是否存在结构变化.LI等[18]基于偏最大似然得分过程构造统计量, 研究了多分类Logistic回归模型的变点序贯检验问题.

本文基于偏似然得分过程构造序贯检验统计量, 在线监测累积Logistic回归模型的结构是否存在变点.原假设下推导出统计量的渐近分布, 备择假设下证明其一致性.与文[17]提出的CUSUM变点监测方法相比, 本文所提出的方法只需要在原假设下估计出模型参数, 备择假设下不需要重新估计.模拟试验表明原假设下统计量的检验水平大部分都接近于显著性水平0.05, 在备择假设下虽然监测到变点的平均运行长度较长, 但监测到变点的误报率较低, 且检验势也较高.最后通过一组实际数据说明本文方法的有效性.

2.模型及变点检验问题

变点的序贯检验统计量一般是由监测统计量Γ(m,k)和边界函数g(m,k)构成.定义停时

Γ(m,k)和g(m,k)在原假设下满足

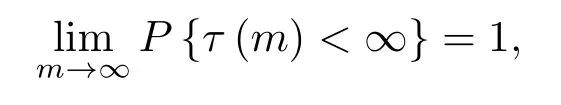
其中α ∈(0,1).

3.变点的序贯检验

首先利用偏最大似然方法对θ进行估计[20], 偏似然函数为

则对数偏似然函数为

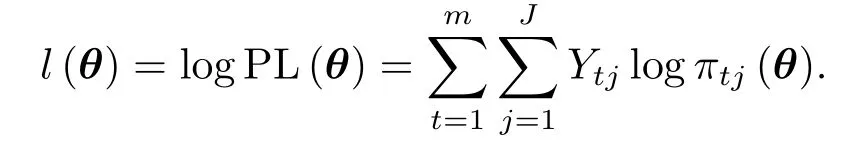
记

其中

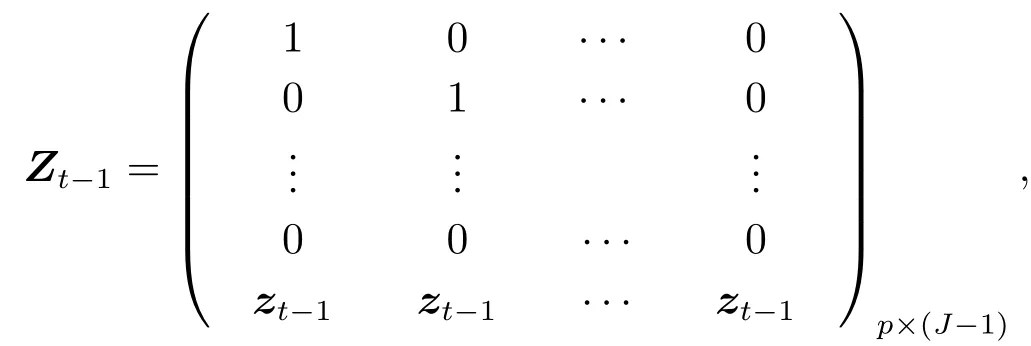
假设1和假设2表明偏对数似然函数的二阶导数是关于θ的连续函数[21].假设2保证了Ut(θ)是非奇异的.假设3表明

知了在树上放肆地叫着，夕阳的余晖照过来，我看到西天堆起大山一样的乌云，一重连一重。一注一注的阳光从乌云的后面射向天空，给绵绵云山缀上了一带炫目的金边。我强撑着爬起来，漫无目的朝前走着。身后不知么事时候，冒出几个细伢儿跟着，他们齐声唱道——

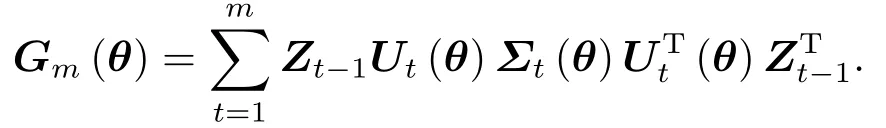
满足正定性的概率是1.[21]若假设4成立, 则当m →∞时

其中G(θ)为正定矩阵.[21]

令Sm(θ)=0, 求解可得θ的偏最大似然估计量基于构造变点序贯检验统计量

g(s)是边界函数.

下面两个定理给出统计量Stat在原假设下的极限分布以及备择假设下的一致性.

定理3.1如果假设1-4和原假设H0成立, 则

(i) 若g(s)=c, 则

由Nκm」, 类似于文[13]中定理1和定理3的证明可得

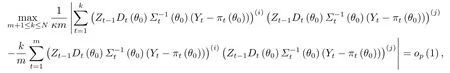
则定理的结论成立.(ii)的证明与(i)类似.

根据假设1-4,

因δ0, 当m →∞时

则(i)的结论成立, 当m+1＜k ＜k*时, 证明是类似的.(ii)的结论可由(i)直接推出.

4.模拟试验

本节利用Monte Carlo模拟研究变点序贯检验统计量Stat的有限样本性质.在推导统计量的渐近分布时, 采用了两种不同的边界函数g(s)=c和g(s)=cg1(s)=cs0.8, 相应的临界值可分别通过下式获得：

其中α是显著性水平.数据生成过程如下：

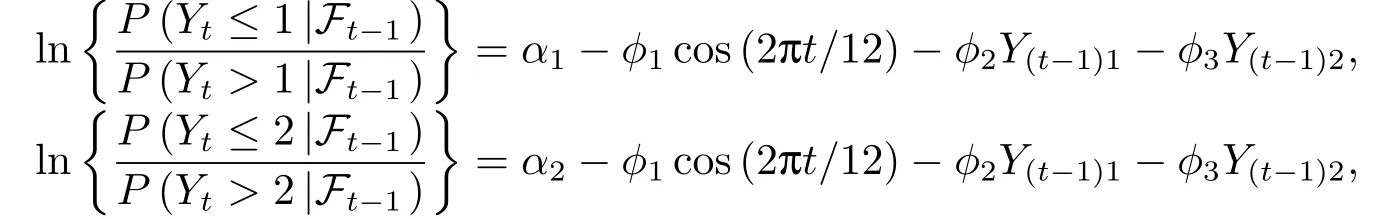
其中{Yt}是类别数为3的累积logistic回归模型,α1=-0.5,α2=0.2,(φ1,φ2,φ3)T=(2,-0.5,1)T.假设历史样本量m= 100,200,500, 监测样本量N1=N -m= (κ-1)m,κ= 3,5,7.显著性水平取α=0.05, 模拟试验重复的次数为2500 次.

令θ= (α1,α2,φ1,φ2,φ3)T, 在现实应用中可能只关注部分参数是否发生变化.本文假设只监测参数α1和φ1是否发生变化, 其余参数作为冗余参数.表1给出了原假设下统计量Stat在两种边界函数下的检验水平.结果表明两种情形下的检验水平大部分都接近于显著性水平0.05, 少部分存在一些扭曲.

表1 两种边界函数下统计量的检验水平

考虑下述形式的备择假设:

HA:α1在m+k*处从-0.5变为-2,φ1在m+k*处从2变为3,

其中k*= 0.01N,0.05N,0.1N,0.2N,0.3N.表2-5描述了统计量Stat的检验势和监测到变点运行长度(Run length)的四分之一分位数(Q1), 中位数(Q2), 均值(Average run length, ARL), 四分之三分位数(Q3), 最大值(Max) 以及误报率(Pτ).运行长度是变点发生位置与监测到变点的位置之间的样本量, 其均值称为平均运行长度(ARL).检验势是监测到变点发生在m+k*之后,N之前的次数所占的比率.ARL≥¯m+k*表示监测到变点位置发生在m+k*之后时, 其运行长度的平均值.误报率是指监测到变点发生在m+k*之前的次数所占的比率.做为对比, 考虑了文[17]中CUSUM变点检测方法, 其临界值可通过模拟平均运行长度的方式获取.假设受控状态下平均运行长度为370, 则相应的临界值为2.5.CUSUM统计量的检验势, 运行长度的数字特征和误报率见表6.

表2 在HA下, 当m=100,N =400, g(s)=c时, Stat的检验势, 运行长度的数字特征和误报率

表3 在HA下, 当m=100,N =400, g(s)=cs0.8时, Stat的检验势, 运行长度的数字特征和误报率

表4 在HA下, 当m=200,N =800, g(s)=c时, Stat的检验势, 运行长度的数字特征和误报率

表5 在HA下, 当m=200,N =800, g(s)=cs0.8时, Stat的检验势, 运行长度的数字特征和误报率

从表2-5的结果可以看出, Stat的检验势随着样本量的增加而增大, 但当变点发生的位置离监测起始时刻越远, 其检验势越低.边界函数不同, 其对应的检验势也有差异.当m=100,N=400时, 边界函数取g(s)=c的检验势高于g(s)=cs0.8时的检验势.但当样本量增大,m=200,N=800时, 两种边界函数下的检验势都趋于1.

运行长度的数字特征Q1,Q2, ARL,Q3, Max随着样本量的增大而增大.变点发生的位置也会对运行长度产生影响.当边界函数取g(s) =c时, 运行长度受变点位置的影响较小.例如当m=100,N=400, 不同变点位置下的平均运行长度是230左右;m=200,N=800, 不同变点位置下的平均运行长度是293左右.但当g(s) =cs0.8时, 不同变点位置对运行长度的影响较大.例如m=100,N=400,k*=0.01N,0.3N时, 平均运行长度分别是156.66和259.13, 差异较大.相比g(s) =c, 边界函数取g(s) =cs0.8时, 若变点的位置离监测起始时刻较近时, ARL较短, 但当变点位置离监测起始时刻较远时, ARL较长.由于误报率在大多数情形下都为0, 变点后的平均运行长度(ARL≥¯m+k*) 与平均运行长度(ARL)几乎都是相等的.

表6 在HA下, 当m=100,N =400, CUSUM变点检测方法的检验势, 运行长度的数字特征和误报率

由表6可以看出, 当利用CUSUM方法监测变点时, 其检验势, 运行长度和误报率受变点位置的影响较大.例如m= 100,N= 400, 当变点发生在监测起始时刻时, 检验势接近于1, 平均运行长度为11.5, 误报率为0; 但当变点的位置离监测起始时刻较远时, 检验势迅速下降, 误报率迅速增加, 此时监测到的变点大都发生在m+k*之前, 所以其平均运行长度为负值.

总的来说, 统计量Stat在两种边界函数下的平均运行长度较长, 但误报率很小, 大多数情况下都为0.CUSUM方法在变点发生在监测起始时刻时, ARL较短, 误报率较低.但当变点发生在离起始时刻较远时, 误报率较高.

5.实例分析

图1是一组新生儿睡眠状态的观测序列, 每隔30秒观测一次, 共1000个观测值.每个时刻的睡眠状态一般可分为四类: 安静睡眠(Quiet sleep), 不确定睡眠(Indeterminate sleep), 主动睡眠(Active sleep), 醒(Awake), 分别记为1, 2, 3, 4.根据新生儿的睡眠规律, 四个睡眠状态有一定的次序, 即“4”＜“1”＜“2”＜“3”, 则观测序列可看作有序分类时间序列.文[20]利用累积logistic回归模型对其进行建模

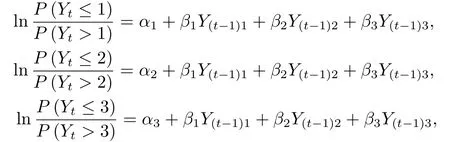
其中α1=-14.722,α2=-10.389,α3=-4.078,β1= 18.663,β2= 12.173,β3= 7.566.采用文[13]的回顾性变点检验(Retrospective change-point detection)方法检测上述模型是否存在结构变点, 结果发现α2在第596个观测值处存在变化.在变点前后对模型参数重新进行估计, 得到调整模型.对比原模型和调整后模型的AIC值, 发现调整后的模型AIC值减小, 即调整后的模型更加合理.用本文所提出的变点序贯检验监测变点, 以前200个数据为历史数据, 从第201个数据开始监测, 发现统计量在第671个数据处停止监测, 监测延迟为175.虽然有一定的监测延迟, 但也能有效监测到变点.

图1 新生儿睡眠状态的观测序列

6.结论

累积Logistic回归模型是分类时间序列建模的一类重要模型.针对累积Logistic回归模型结构变点的序贯检验问题, 本文基于偏似然得分过程构造统计量, 在线监测模型的结构是否存在变点.在原假设下推导出统计量的渐近分布, 备择假设下证明其一致性.模拟试验采用了两种形式的边界函数,结果表明原假设下统计量的检验水平大部分都接近于显著性水平0.05, 少部分存在一些扭曲.在备择假设下虽然监测到变点的平均运行长度较长, 但监测到变点的误报率较低, 且检验势也较高.CUSUM变点检测方法在变点发生在监测起始时刻时, ARL较短, 误报率较低.但当变点发生在离起始时刻较远时, 误报率较高.最后通过一组新生儿睡眠状态的观测数据说明本文方法的有效性.