与分数阶热半群相关的平方函数刻画Hardy空间
王志永, 赵凯
(青岛大学数学与统计学院,山东 青岛 266071)
1.引言
由于欧式空间上的实变量Hardy空间在偏微分方程的研究中起到了至关重要的作用,所以该空间的相关理论自上世纪七十年代以来被大量的研究, 许多重要的结果被相继的建立起来.令Δ是Rn上的Laplace算子, 众所周知, 经典的Hardy空间H1(Rn)可以通过极大函数supt>0|e-t(-Δ)f(x)|来刻画.[10]从某种意义上讲, 该结果表明经典的Hardy空间H1(Rn)可以看作是与-Δ相关的Hardy空间.作为经典理论的推广, 自二十世纪九十年代与微分算子相关的Hardy空间理论开始得到许多研究者关注.在Rn空间上,n ≥3, 令L=-Δ+V, 其中位势V属于逆Hlder类.1999年, Dziubanski和Zienkiewicz在文[3]中引入了与L相关的Hardy空间(Rn), 并且借助于局部Hardy空间建立了H1L(Rn)的原子刻画和Riesz变换刻画.进而借助于Campanato型空间, 在文[4]中, Dziubanski和Zienkiewicz引入了更一般的Hardy型空间Rn),p <1.自此之后, 文[3-4]的结果被推广到其他二阶微分算子, 并且许多与算子相关的函数空间被相继建立起来, 参见文[1,11-12].
令f是Rn上的局部可积函数,B=B(x,r)表示Rn中以x为中心且以r为半径的球.fB表示f在球B上的平均, 即fB=|B|-1令

则称f属于Campanato型空间(Rn).
引理1.1[9]令0<γ ≤min{1,2α,δ0},Hardy型空间(Rn)的对偶空间是Campanato型空间(Rn).
与L相关的极大函数定义为ML(f)(x):=supt>0|e-tL(f)(x)|,则Hardy型空间(Rn)的定义如下:
定义1.2对于0<γ ≤min{1,2α,δ0},Hardy空间(Rn)定义为所有((Rn))*中满足极大函数属于Ln/(n+γ)(Rn)的分布f的全体.其范数为

众所周知, 平方函数刻画在证明奇异积分算子在Hardy型空间中的有界性中起到了至关重要的作用.在文[5]中, Fefferman和Stein给出了经典Hardy型空间Hp(Rn)的平方函数刻画.自此以后, 此类刻画被推广到了其他情形, 参见文[3-4,12].定义
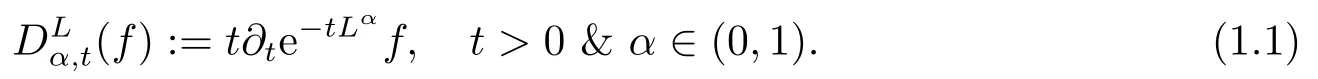
利用(1.1), 我们引入与分数阶热半群{e-tLα}t>0相关的Lusin面积函数
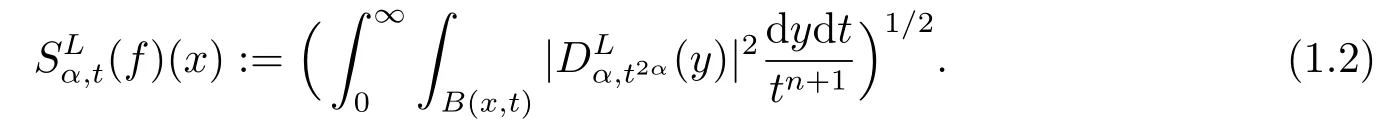
这篇文章的主要目的是借助于由(1.2)定义的平方函数去刻画Hardy型空间(Rn).
在本文的剩余部分, 我们用C和c来表示正的常数.这些常数仅仅与空间的维数, 函数空间的指标以及某些与Schringer算子相关的参数有关, 故这些常数在不同的地方可能取不同的值.所谓B1~B2, 是指存在一个常数C >1, 使得1/C ≤B1/B2≤C.
2.帐篷空间以及基本性质
如果存在C >0, 使得对任意的球B ⊂Rn, 逆Hlder不等式
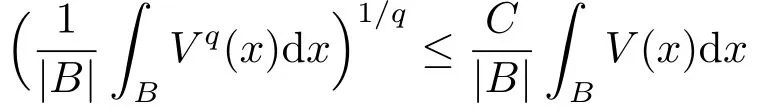
成立, 则非负位势V属于逆Hder类Bq, 1<q <∞.本文中, 我们假设02.
令δ0=2-n/q,δ=min{1,δ0}并且n/(n+δ)<p ≤1, 如果函数a满足


帐篷空间的原子定义如下:
定义2.2如果函数α(·,·)满足

3.分数阶热核的正则性
命题3.1[4](i) 对任意的N >0, 存在CN,c >0, 使得

接下来, 我们考虑与L相关的分数阶热半群.对于α ∈(0,1), 用Lα表示算子L的分数次幂,其定义为

通过从属性公式(3.1)和命题3.1, 在文[8]中, LI等人证明了
命题3.2[8]令0<α <1.
(i) 对任意的N >0, 存在常数CN >0, 使得
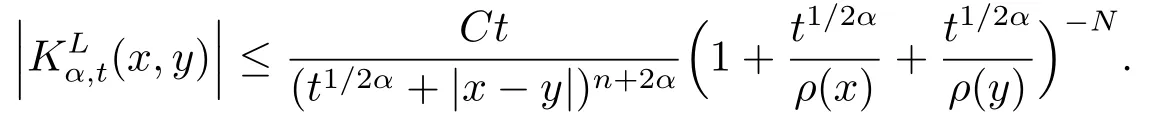
(ii) 令0<δ′ ≤min{1,2α,δ0}.对任意的N >0, 存在常数CN >0, 使得对任意的|h| ≤t1/2α,

对于t >0, 定义

在文[8]中, LI等人给出了核函数(·,·)的下列估计.
命题3.3[8]令0<α <1.
(i) 对任意的N, 存在常数CN >0, 使得
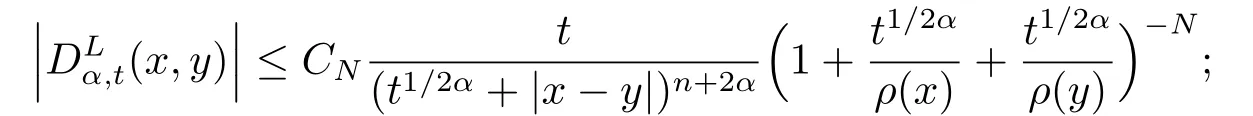

4.Hardy空间的平方函数刻画
我们首先给出几个必要的引理:

所以我们把以下的证明分为两部分, 首先我们验证(4.1).利用命题3.3, 可知
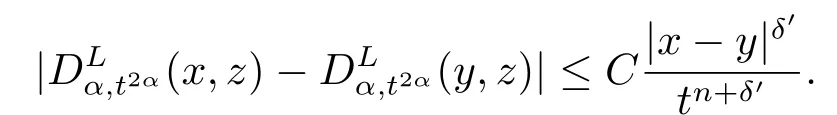
当γ=δ′ ≤min{1,2α,δ0}, 可以得到
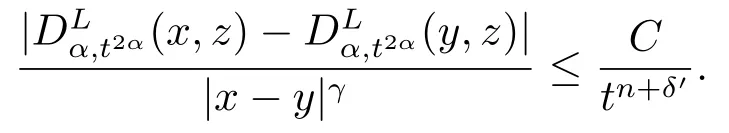
其次, 我们验证(4.2), 再次利用命题3.3, 可知

取N=γ, 有
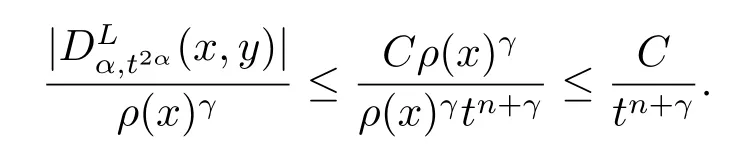


对于x ∈Bc(x0,2r)和y ∈B(x0,r), 则|x-y|~|x-x0|.考虑以下两种情况:
情形1α ∈(1/2,1).在这种情形下, 令l=n+1, 得到

最后我们有

这就完成了本定理的证明.
- 应用数学的其它文章
- 不确定离散时间输入饱和系统的鲁棒预见控制
- Maximal Operator of (C,α)-Means of Walsh-Fourier Series on Hardy Spaces with Variable Exponents
- Empirical Likehood for Linear Models with Random Designs Under Strong Mixing Samples
- 带分数阶边值条件的差分方程组的正解问题
- An Interior Bundle Method for Solving Equilibrium Problems
- 纵向数据下非参数带测量误差的部分线性变系数模型的估计

