含源反应扩散方程的两类修正差分格式

张静, 王彩华

(天津师范大学数学科学学院,天津 300387)

1.引言

奇异扰动方程一般是指微分方程中最高阶导数项含一个小参数, 此类问题广泛出现在应用数学和工程学的许多领域.求解奇异扰动方程的方法有很多, 如有限差分法[1-2]、有限元法[3-4]、有限体积法[5-6]等.本文研究一种奇异扰动两点边值问题: 含参数ε的含源反应扩散问题, 其微分方程模型为

针对一维对流扩散反应方程的数值解有较多研究, 如文[7]根据一阶和二阶导数的padé型紧致差分格式推导出一种四阶格式; 文[8]首先研究常系数情形下的差分格式, 然后在此基:上修正, 提出了变系数对流扩散反应方程的指数型高精度差分格式; 文[9]引入了指数拟合因子,结合等距网格给出了一种有限差分格式, 适合于求解具有双边界层的两点边值问题.

针对反应扩散模型(1.1), 文[10]设计了一种六阶三点差分格式FD1[10]:

其中

文[11]针对对流扩散反应方程提出了差分格式FD2[11], 应用于模型方程(1.1)得到如(1.2)的三点格式, 其中

该格式具有四阶精度.本文实验部分主要与文[10-11]给出的差分格式进行了数值比对.

虽然奇异扰动问题已有较多数值方法, 但一些方法适用于参数较大的情形, 当边界层非常窄时失效, 能否设计出精度更高, 适用性更强的数值格式仍值得进一步研究.文[12]针对无源对流扩散问题设计了两类修正差分格式: 其横向系列修正格式结合等距网格能高精度求解参数不是很小的对流扩散问题, 精度可分别达到二阶、四阶、六阶和八阶, 其纵向格式能高精度求解参数很小时的对流扩散问题, 数值实验表明, 文[12]提出的两类方法与八种参考格式比对数值结果更好.本文拟沿用文[12]的差分格式设计思路, 展开对反应扩散问题数值解的研究.

为表述简单, 下文的系列横向差分格式简记为HDS1, HDS2, HDS3 (HDS: Horizontal Difference Scheme)等; 纵向差分格式记为VDS1, VDS2 (VDS: Vertical Difference Scheme)等.

2.横向与纵向系列修正差分格式的设计思路

设函数u(x)充分光滑, 当i= 1,2,··· ,N -1时, 三点模板上将ui-1、ui+1在点xi处进行Taylor展开

于是, 当n=2,3,···时, 递推公式为

依据递推公式(2.5), 可列出u(x)的部分高阶导数降阶组式如下

横向系列差分格式设计思路: 当ε不是很小时,把(2.6)中部分降阶式代入泰勒展式(2.1),(2.2)中, 关于h的幂次保留的项数不同则截断误差不同.例如, 式(2.1),(2.2)只取到u′′(x)项, 整理后可得到二阶差分格式HDS1(即中心差分格式CDS); 式(2.1),(2.2)如保留到u(3)(x),u(4)(x)项,整理后可得四阶差分格式HDS2; 继续修正可得六阶差分格式HDS3.

纵向系列差分格式设计思路: 当ε非常小时, 纵向观察组式(2.6), 考虑含1/ε的负指数幂次越大的项其绝对值可能越大.如组式(2.6)仅保留纵向关于1/ε指数幂次最大项代入泰勒展式(2.1),(2.2), 舍去其它项, 整理可得纵向差分格式VDS1; 在VDS1的基:上继续修正,保留1/ε指数幂次最大项及次大项, 整理可得纵向差分格式VDS2; 类似地, 进一步修正可得VDS3等.

如需进一步提高数值解的精度, 且不考虑计算机舍入误差, 横向、纵向差分格式可一直修正下去.

3.横向系列修正差分格式

Ⅰ 二阶横向差分格式HDS1(中心差分格式CDS)

由带微分余项的Taylor展式知

其中ξi ∈(xi-1,xi+1).将式(3.3)代入到式(1.1)中, 并整理可得

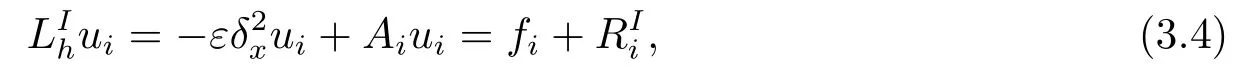
其中

忽略(3.4)式右端的二阶小量, 并记ui的近似值为Ui, 可得差分格式HDS1

该格式即为我们熟知的二阶中心差分格式(CDS).

Ⅱ 四阶横向差分格式HDS2

由Taylor展式及降阶式(2.3)有

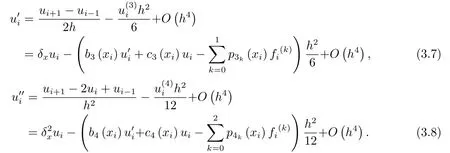
将等式(3.7)左右的移项合并, 并整理得

其中

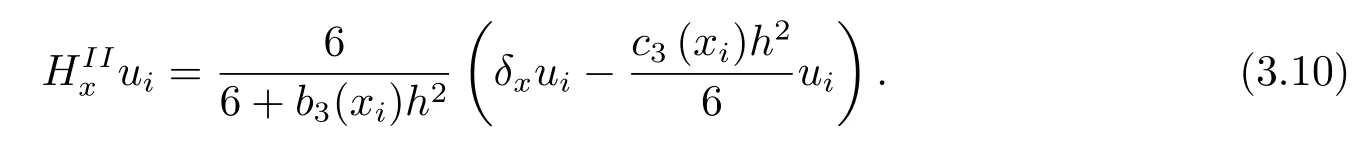
将式(3.9)代入式(3.8), 整理得

其中

将式(3.11)代入到微分方程式(1.1)中, 可得

其中

去掉式(3.13)中小量, 并用近似值Ui代替上式的ui, 可得差分格式HDS2

其截断误差为四阶.将(3.15)写成三点紧凑格式如下

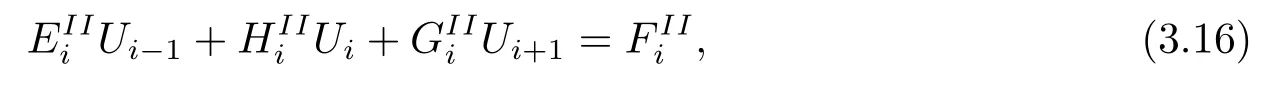
其中

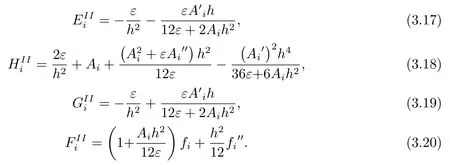
Ⅲ 六阶横向差分格式HDS3

由Taylor展式以及降阶式(2.3)有

将式(3.21)中项合并，并整理得

其中

将式(3.23)代入式(3.22), 整理得

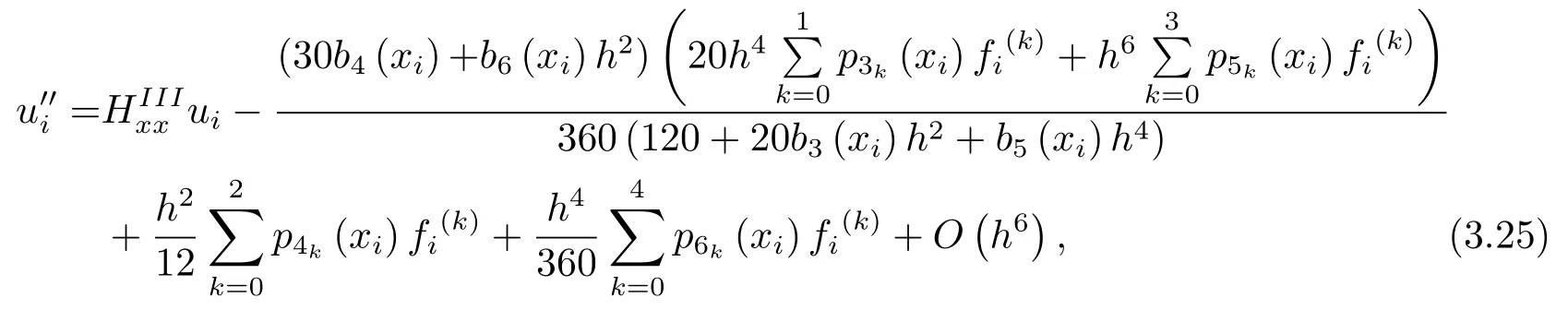
其中

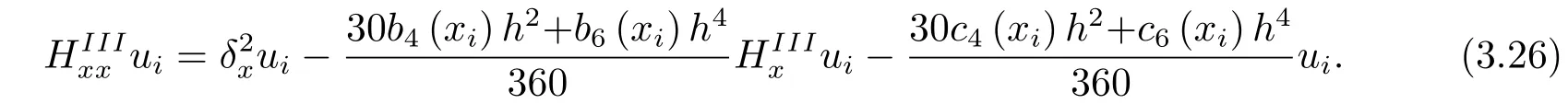
将式(3.25)代入到微分方程式(1.1)中, 并整理, 得

其中

忽略式(3.27)右端小量, 可得差分格式HDS3

其截断误差为六阶.

4.横向差分格式的收敛性分析

Ⅰ 中心差分格式(CDS)的收敛性分析

引理4.1(极值原理)设V={Vi|i ∈是上的网格函数, 差分算子由(4.1)给出,A(x)≥0(x ∈[a,b])成立, 如果

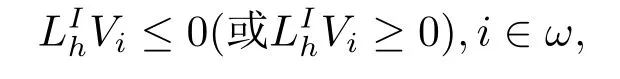
则有

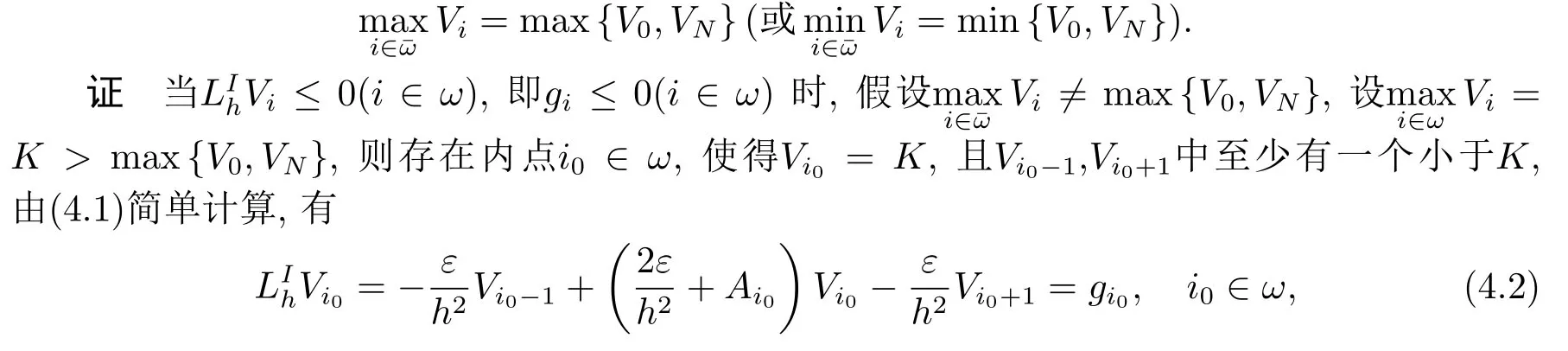
整理得

当差分方程组(4.1)为齐次右端与齐次边界条件时, 由引理4.1知其只有零解, 从而差分格式CDS唯一可解.

引理4.2设V={Vi|i ∈}是网格上任意的网格函数,差分算子由(4.1)给出,如A(x)≥Amin＞0(x ∈[a,b])成立, 有

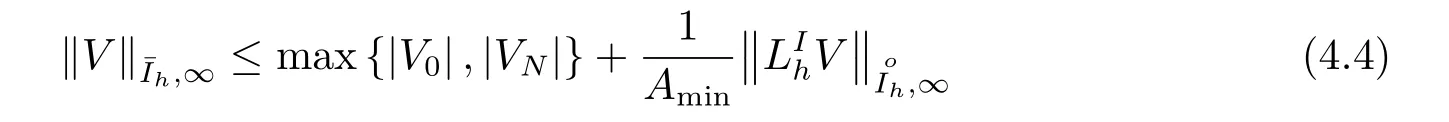
证取障碍函数(barrier function)

简单计算知

令

上式两端作用差分算子, 有

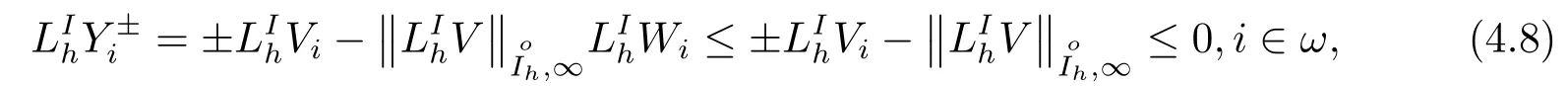
因而有

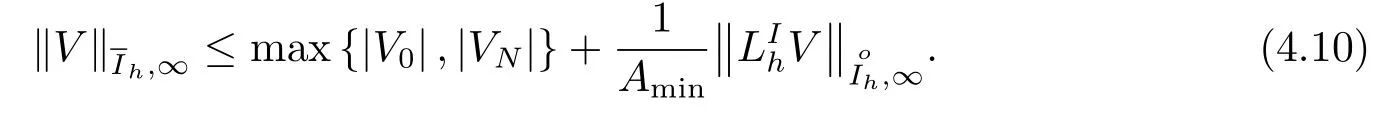
证明完毕.

定理4.1Ui是差分格式CDS即(3.6)的解,ui是微分方程(1.1)在结点处的精确值,当A(x)≥Amin＞0(x ∈[a,b])成立, 有

其中M1=‖-Af+A2u+ε(2A′u′+uA′′-f′′)‖∞.

证记误差为

则由(3.4),(3.6)式有误差方程

且

故定理4.1成立.

针对微分方程(1.1), 一般A(x)≥0且函数A(x),f(x)满足一定的光滑性, 该方程就是可解的, 中心差分格式可以进行数值计算.下面我们对一般情形A(x)≥0(x ∈[a,b])(不一定有A(x)≥Amin＞0)时中心差分格式的误差进行估计.

引理4.3设V={Vi|i ∈}是网格上任意的网格函数,差分算子由(4.1)给出,当A(x)≥0(x ∈[a,b])时, 有

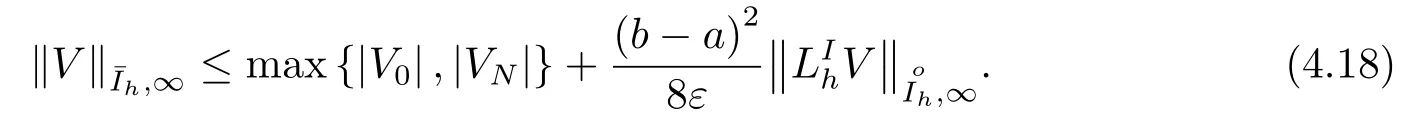
证取障碍函数

简单计算知

令

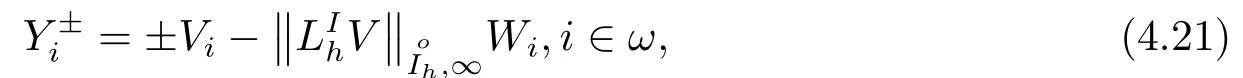
上式两端作用差分算子, 有

因W(x)＞0,x ∈(a,b), 由引理4.1有

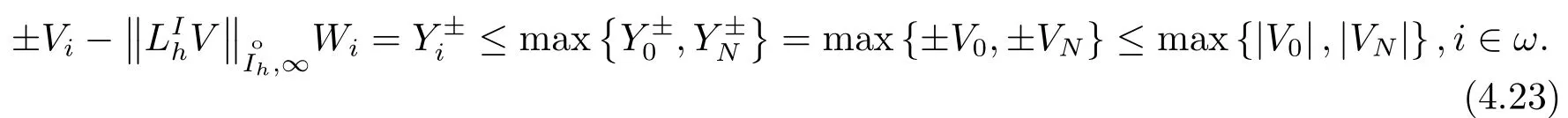
证明完毕.

定理4.2Ui是差分格式CDS即(3.6)的解,ui是微分方程(1.1)在结点处的精确值,当A(x)≥0(x ∈[a,b])时, 有

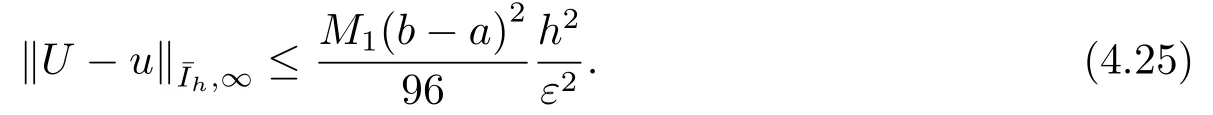
证在本定理条件下, 首先同定理4.1一样, 知式(4.16)即仍成立, 再结合引理4.3得故定理4.2成立.

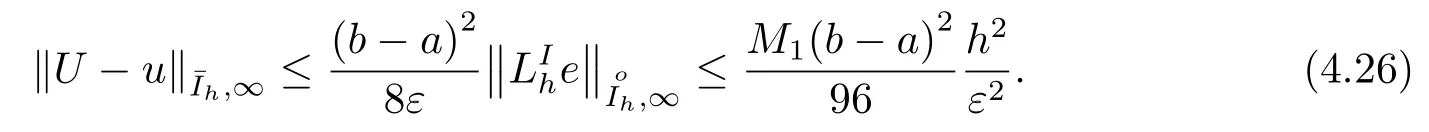
注4.21)关于定理4.1的相关注解对本定理仍然成立; 2) 当A(x)≥Amin＞0 (x ∈(a,b))可使用定理4.1的误差估计, 当仅有A(x)≥0(x ∈[a,b])时可使用定理4.2的误差估计.

Ⅱ 横向差分格式HDS2、HDS3的收敛性分析

利用带微分余项的泰勒公式计算, 可得

设差分方程组为

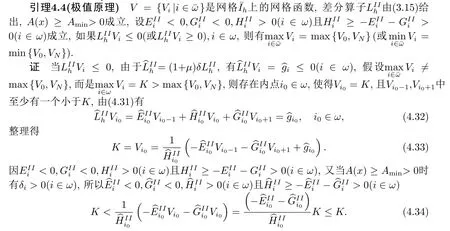
当差分格式HDS2的算子满足引理4.4的条件时, 显然齐次差分方程组只有零解, 从而差分格式HDS2唯一可解.

定理成立.

式(3.29)给出了HDS3格式, 泰勒展开可知

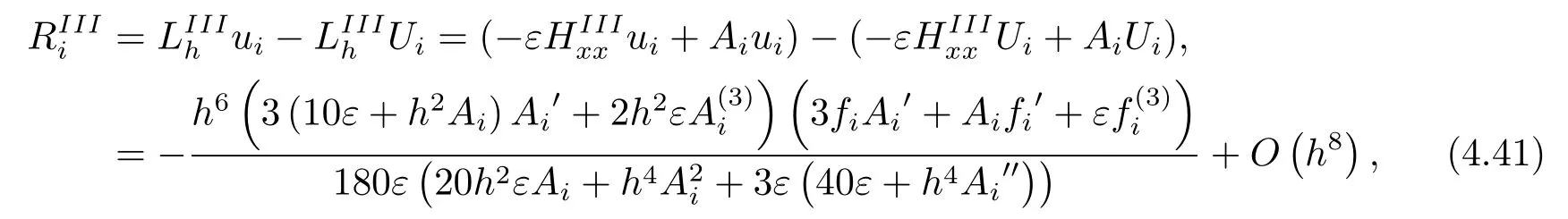
截断误差为六阶, 可类似HDS2一样进行误差分析, 省略.

5.纵向系列修正差分格式

将降阶式(2.3)分别代入式(2.1), (2.2)有

将上两式(5.1)与(5.2)简写成

其中

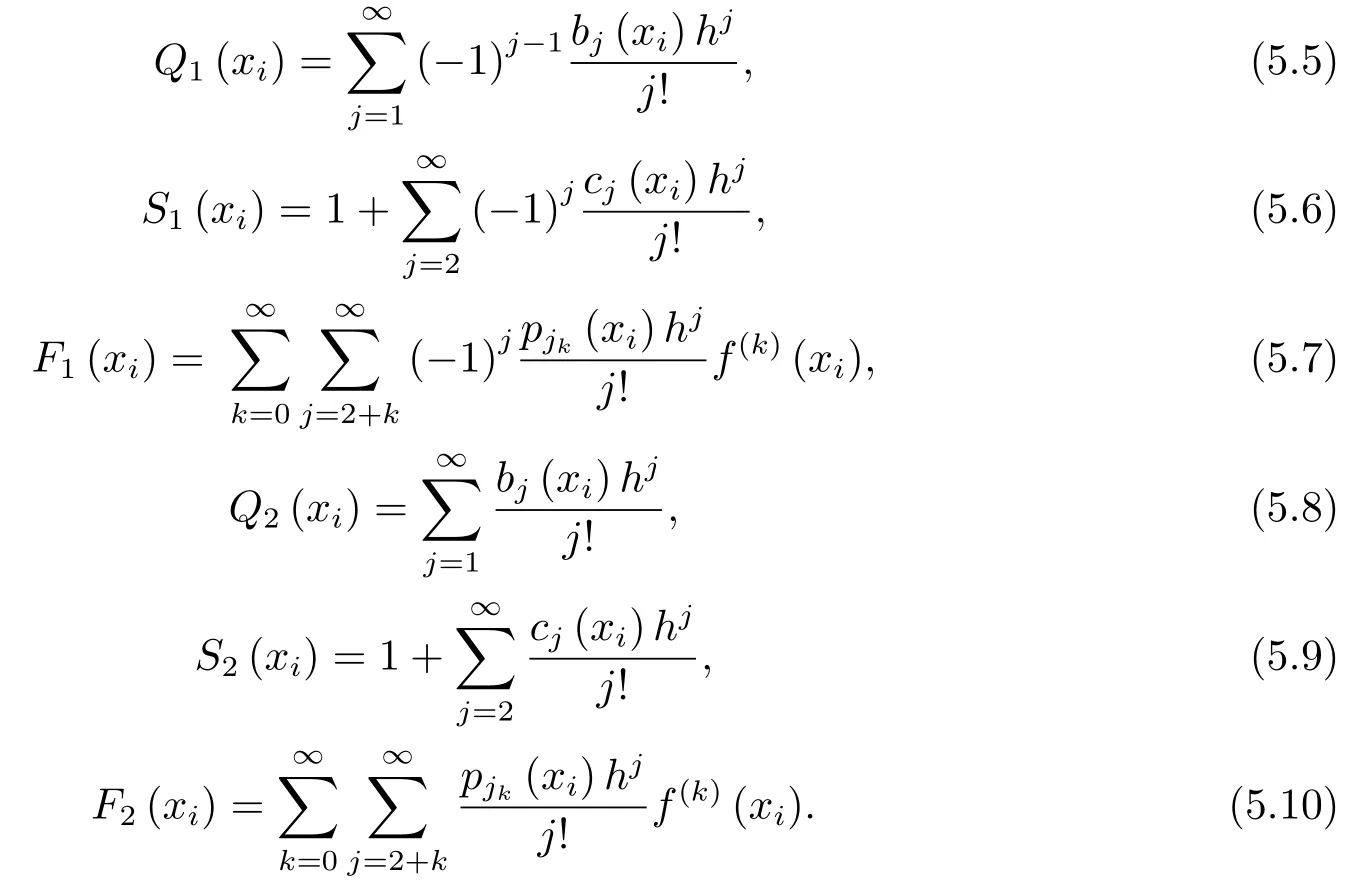
联立式(5.3),(5.4), 消去得到

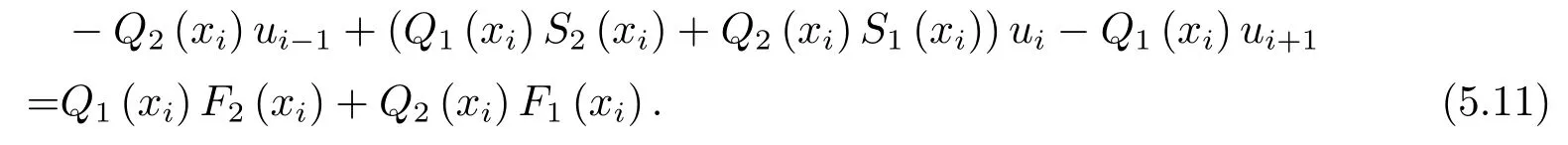
上式是无任何误差形式精确的差分格式, 下面的关键是如何对Q1(x),Q2(x),S1(x),S2(x),F1(x),F2(x)保留有限项进行截断.

bj(x)、cj(x)、pjk(x)由(2.5)式, 利用Mathematica软件符号推导容易写出其具体表达式,下面列出其部分式如下.

观察(5.5)和(5.8)式,Q1(x),Q2(x)中含有级数项bj(x)(j=1,2,···), 由递推公式(2.5), 可算出

观察(5.6)和(5.9)式, 由递推公式(2.5), 可算出S1(x),S2(x)中含有的无穷项cj(x)(j=1,2,···)的表达式如下

观察(5.7)和(5.10)式, 对于F1(x),F2(x)中的pjk(j=k+2,k+3,··· , k= 0,1,2,···), 由递推公式(2.5), 我们归纳如下.

首先，下面组式是F1(x),F2(x)中关于f(x)的系数表达式pj0(x)(j=2,3,···)

其次,f′(x)的系数表达式pj1(x)(j=3,4,5,···)

一般地,f(k)(x)的系数表达式pjk(x)(j=k+2,k+3,···)为

Ⅰ 纵向差分格式VDS1

将A(x),f(x)看成常数A,f,bj(x)、cj(x)、pj0(x)分别保留式(5.12)、(5.13)与(5.14)的第一列作为其近似, 代入(5.5)-(5.10), 整理可得纵向差分格式VDS1

其中i=1,2,··· ,N -1, 且U0=α, UN=β,

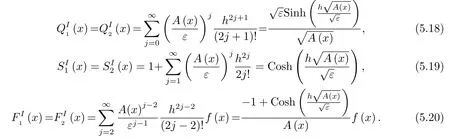
上三式代入(5.17), 整理可得VDS1的三点式

Ⅱ 纵向差分格式VDS2

在差分格式VDS1基:上进一步修正, 分别保留式(5.12)、(5.13)与(5.14)的前两列作为bj(x)、cj(x)、pj0(x)的近似, 代入(5.5)-(5.10), 整理可得纵向差分格式VDS2

其中i=1,2,··· ,N -1, 且U0=α, UN=β,

Ⅲ 纵向差分格式VDS3

在差分格式VDS2基:上进一步修正, 其中Q1(x),Q2(x),S1(x),S2(x)仍以VDS2中的式(5.22)-(5.25)近似,而(5.7)式F1(x)与(5.10)式F2(x)保留到f′′(x)项.对于pj0(j=2,3,···),pj1(j=3,4,···), 和pj2(j=4,5,···)分别保留第一列, 有

将式(5.22)-(5.25)和式(5.28)-(5.29)代入式(5.11), 可以得到如下差分格式VDS3

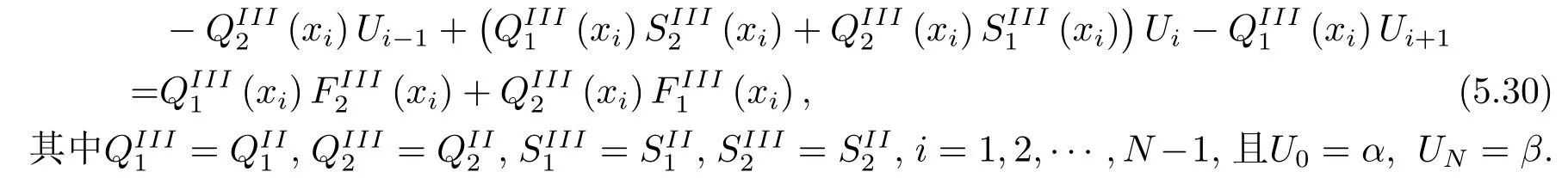
6.数值实验

例6.1含源反应扩散方程

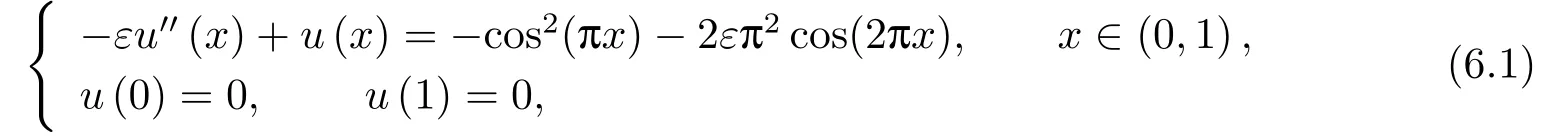
精确解为

由图6.1可见, 当参数较小时该解出现双边界层.

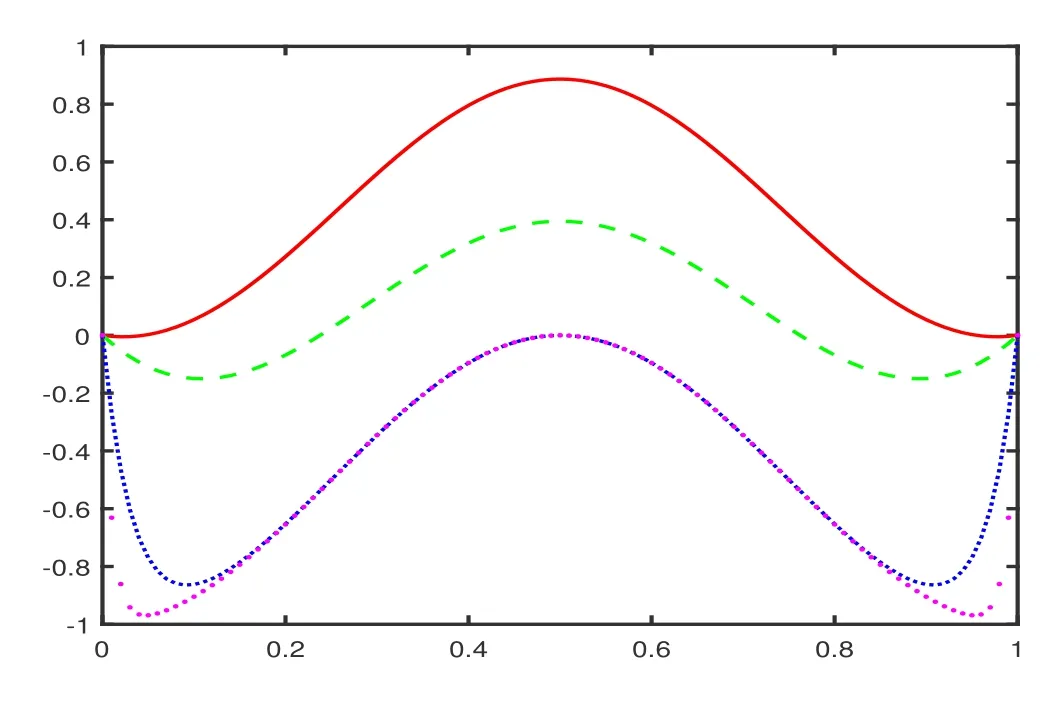
图6.1 参数不同时算例6.1的精确解图

为把舍入误差影响降低到最小, 以便能考察截断误差实际精度, 以下各种差分格式结果均是Mathematica软件设定高精度(如ε=0.1精度设置为50)后编程.

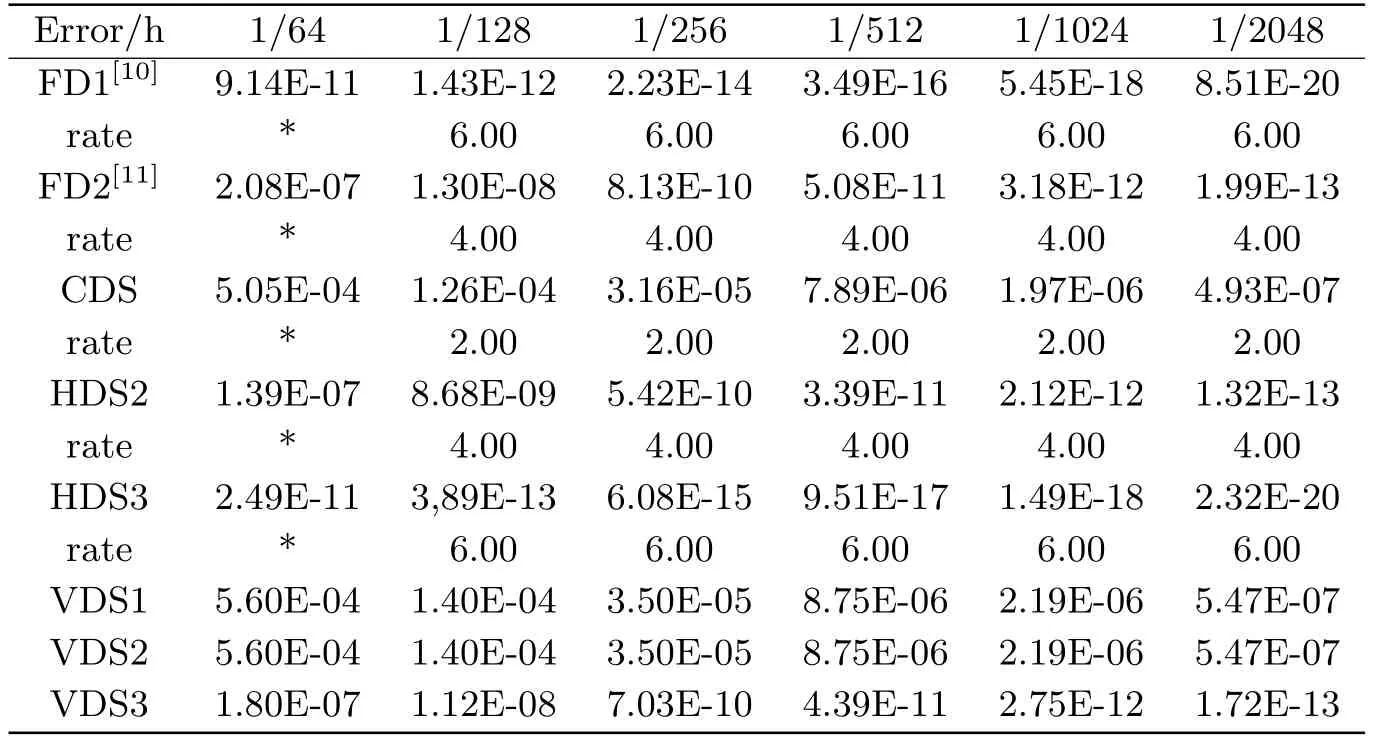
表6.1 算例6.1, 当ε=0.1 各种格式的最大误差

针对例题1, 因A(x) = 1为常函数, 此时VDS1与VDS2格式是相同的.由表6.1可看出, 数值结果精度由高到低为: HDS3, FD1, HDS2, VDS3, FD2, CDS, VDS1 (VDS2),且HDS3和HDS2数值结果明显优于纵向系列差分格式, 说明当参数ε较大时, 横向差分格式HDS3、FD1、HDS2更适用.

减小参数ε的值, 由表6.2可看出, 数值结果精度由高到低约为: VDS3, HDS3, FD1, HDS2,FD2, VDS1 (VDS2), CDS, 纵向格式VDS3的数值精度优于HDS3.

继续减小参数ε的值, 由表6.3可以得到, 数值方法精度由高到低约为: VDS3, VDS1 (VDS2), HDS3, FD1, HDS2, FD2, CDS, 纵向系列差分格式效果整体优于横向系列差分格式, 说明纵向系列差分格式更适用于小参数反应扩散问题.

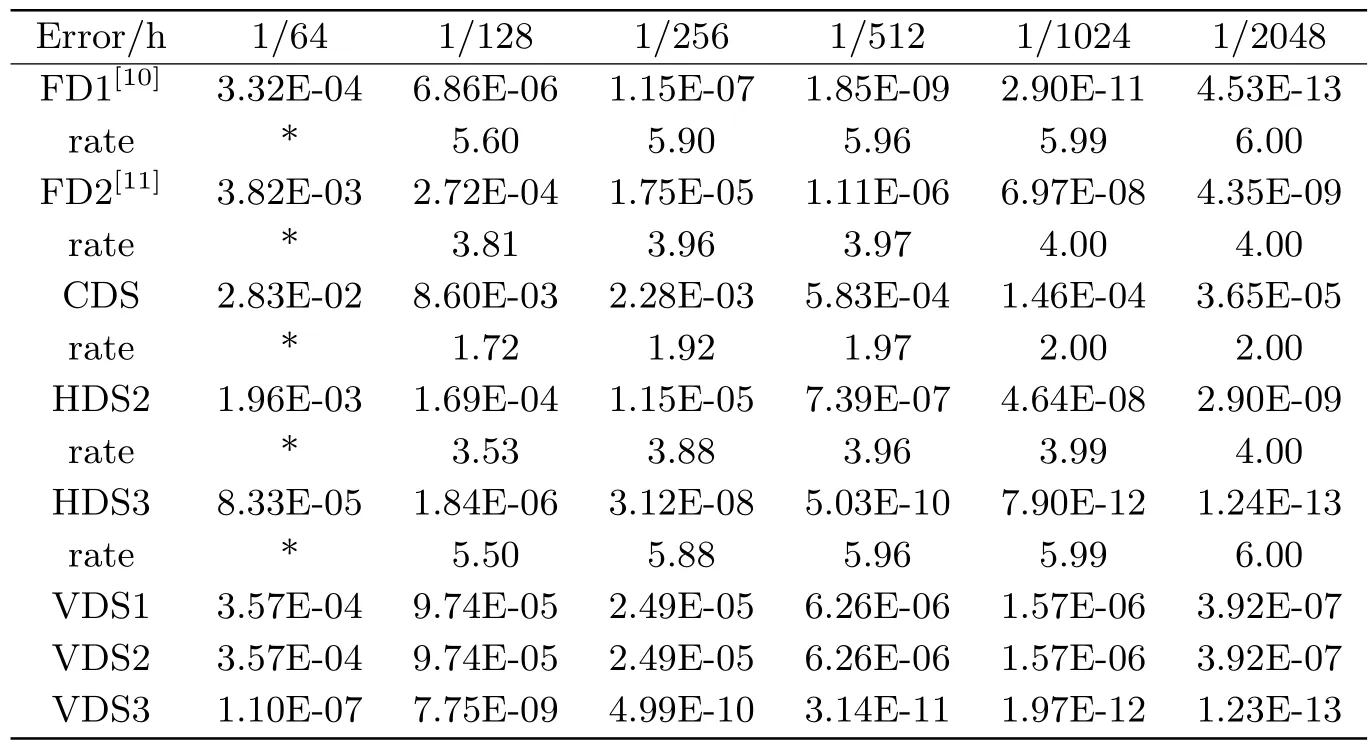
表6.2 算例6.1, 当ε=0.0001 各种格式的最大误差

表6.3 算例6.1, 当ε=10-7 各种格式的最大误差

下面给出反应项系数为变系数的算例实验.

例6.2含源反应扩散方程

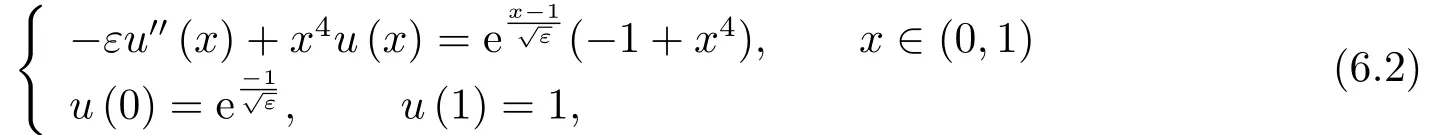
精确解

当参数较小时该解出现右边界层.当参数不太小时, 数值结果能得到与算例1类似的结论,篇幅所限, 下面仅给出ε=10-7的实验结果.

表6.4 算例6.2, 当ε=10-7 各种格式的最大误差

由表6.4可以得到, 当ε=10-7时, 数值方法精度由高到低为: VDS3, VDS2, VDS1, HDS3,HDS2, CDS, FD1, FD2.因此变系数情形下仍得到同样的结论: 纵向系列差分格式更适宜于求解小参数反应扩散问题.

由两个数值算例可以看出: 针对含源反应扩散问题, 中心差分格式虽然不会出现振荡现象,但是数值精度较低.当参数ε不是非常小时, 本文设计的横向系列修正格式HDS3, HDS2适用,但是随着参数ε进一步减小, 纵向系列差分格式逐渐优于横向系列修正格式, 更适用于小参数问题的求解.

本文设计的差分格式可结合非等距网格剖分, 从而能更细致地刻画解在边界层内的变化.另外, 一维降阶思想如何应用于二维奇异扰动问题数值方法设计, 是我们进一步研究的方向.