一个自适应Dai-Liao共轭梯度法

段复建, 杨冲, 李向利

(桂林电子科技大学数学与计算科学学院, 广西 桂林 541004)

1.引言

对于无约束优化问题

其中f: Rn →R是连续可微函数.g(x)是f(x)的梯度函数, 即g(x) =∇f(x).共轭梯度(CG)法是求解(1.1)常用的迭代方法之一, 具有算法简单, 储存需求低等优点.给定初始点x0∈Rn, 共轭梯度算法迭代产生点列{xk}如下

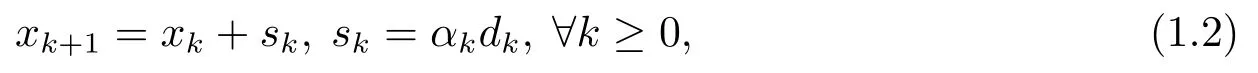
其中步长αk ＞0,dk是搜索方向, 且

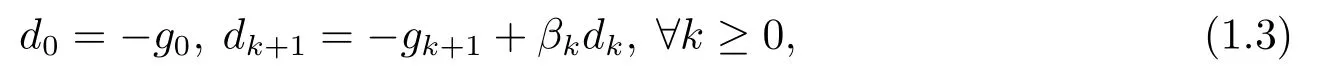
其中gk=∇f(xk),βk是共轭参数.

步长αk由线搜索确定.Wolfe非精确线搜索是最常用的线搜索之一, 它要求αk满足

其中0＜δ ＜σ ＜1.在共轭梯度法的收敛性分析和数值实现中, 步长αk通常也由强Wolfe线搜索计算, 此时步长αk要满足式(1.4)和

根据搜索方向dk的迭代格式(1.3)可以看出, 共轭参数βk的不同选取对应不同的共轭梯度法, 经典的βk公式包括Hestenes-Stiefel(HS)[1], Fletcher-Reeves(FR)[2], Polak-Ribière-Polyak(PRP)[3-4]和Dai-Yuan(DY)[5], 它们的计算公式分别为

其中‖·‖表示Euclidean范数.

随着共轭梯度法不断地深入研究, 2001年, 基于标准的共轭条件= 0, 并结合拟牛顿法的思想, DAI和LIAO[6]提出一个新的共轭条件

其中yk=gk+1-gk, 参数t ＞0.由式(1.3)和(1.6)得到共轭参数

Hager和ZHANG[7]指出参数t的不同选择, 数值结果有较大差异.文[7]中共轭参数形式为

Babaie-Kafaki和Ghanbari[8]将DL方法的搜索方向转化成如下形式

其中

同时, 文[8]指出在迭代过程中矩阵条件数会影响数值稳定性, 并得到矩阵Qk+1的一个谱条件数上界

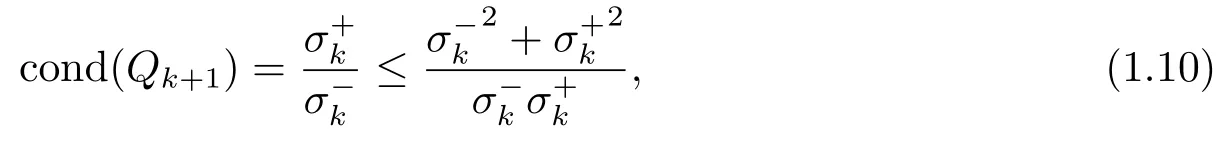
并且有

2018年, 文[9]借助式(1.10), (1.11)和(1.12), 提出了关于参数t的两种不同选取方式

2020年, 文[10]提出了参数t另一种自适应形式

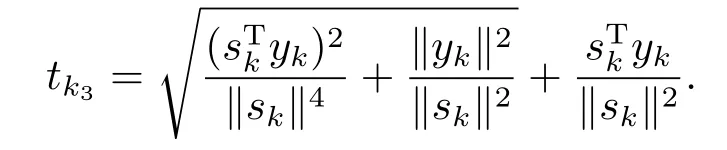
2.一个自适应DL共轭梯度算法

本节, 在文[8-10]的基础上, 提出一个关于参数t的自适应形式

其中θ ＞0是一个变化实参数.将式(2.1)代入到式(1.11)和(1.12)得到

将式(2.2)和(2.3)代入到式(1.10), 于是有

令

为了使cond(Qk+1)的上界尽可能小, 求得h(θ)的极小值点

由式(2.1)和(2.4), 参数t选取如下

类似文[11]中的修正方法, 由式(1.7)和(2.5)得到共轭参数

根据上述共轭参数βk的选取, 进而确定搜索方向dk.在强Wolfe线搜索条件下, 提出一种自适应DL共轭梯度算法.

算法2.1自适应DL共轭梯度算法(NADL)

步0 给定初始点x0∈Rn, 参数ε ＞0, 0＜δ ＜σ ＜1.令k=0,d0=-g0;

步1 若‖gk‖∞＜ε, 则算法终止; 否则, 进行步2;

步2 由强Wolfe条件(1.4)和(1.5)确定步长αk;

步3 计算xk+1=xk+αkdk,gk+1=∇f(xk+1);

步4 由式(2.6)和(1.3)分别计算共轭参数βk和搜索方向dk;

步5 令k:=k+1, 并返回步1.

在共轭梯度法中, 搜索方向dk的下降性具有重要意义.因此, 下面讨论算法2.1中搜索方向dk的下降性.

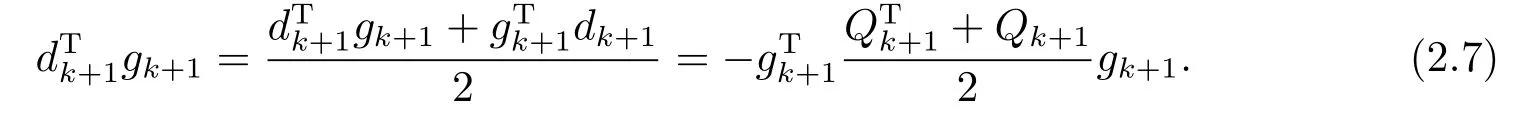
定义对称矩阵

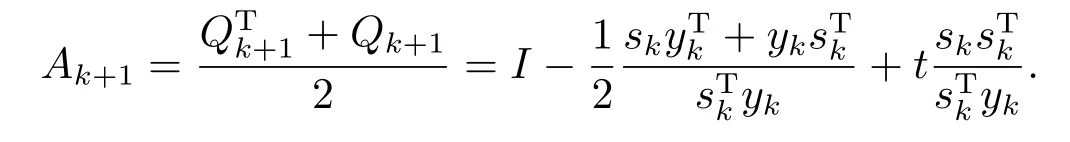
当

对称矩阵Ak+1的最小特征值

此时对称矩阵Ak+1是正定的.因此, 由式(2.7)有

从而搜索方向dk满足下降条件.

对于本文提出的参数tk4, 容易验证其满足关系式(2.8), 从而说明式(1.3)和(2.6)所确定的搜索方向dk对于充分下降条件成立, 即存在一个常数c ＞0, 有

3.收敛性分析

首先回顾一致凸函数的定义.

定义3.1[13]设S ⊂Rn是非空开凸集,φ:S →R是一致凸函数, 即存在一个常数μ ＞0, 有

基于定义3.1,φ是一致凸函数当且仅当

在本节, 当目标函数f(x)是一致凸函数, 在如下假设条件下, 证得算法2.1具有全局收敛性.

假设3.11)f(x)在水平集Ω={x ∈Rn|f(x)≤f(x0)}上有下界, 即存在常数B ＞0, 有

2)f(x)在水平集Ω的某邻域N内连续可微, 且g(x)满足Lipschitz条件, 即存在常数L ＞0,使得

基于假设3.1, 则存在一个常数γ ＞0, 使得

为了证得算法2.1具有全局收敛性, 在假设3.1的前提下, 有如下引理.

引理3.1[14]目标函数f(x)满足假设3.1, 共轭梯度法由式(1.2)和(1.3)迭代计算, 搜索方向dk是下降方向, 步长αk由强Wolfe条件(1.4)和(1.5)确定, 若有

则

定理3.1目标函数f(x)是一致凸函数, 且满足假设3.1, 在算法2.1中, 共轭参数βk由式(2.6)计算, 搜索方向dk由(1.3)确定, 步长αk由强Wolfe条件(1.4)和(1.5)确定, 则有

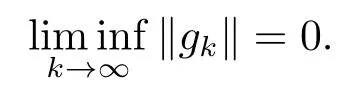
证目标函数f(x)是一致凸函数, 由式(3.1)可得, 存在一常数μ ＞0, 有

由式(3.4)和(3.2), 可以得到

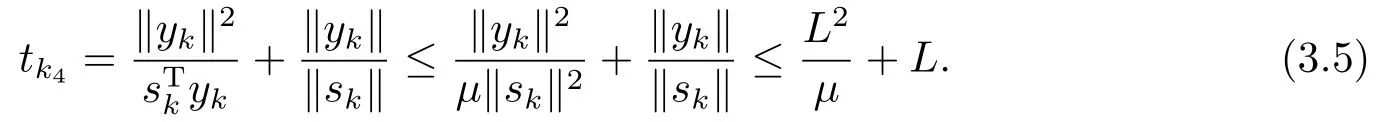
由式(1.3), (2.6), (3.3), (3.4)和(3.5)得到

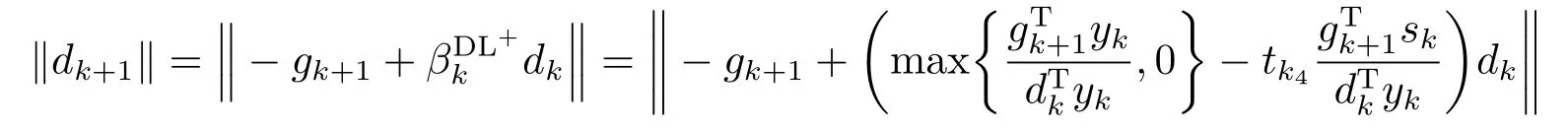
于是证得搜索方向dk有上界, 从而

成立, 由引理3.1可得

4.数值试验

在本节, 将文[7]提出的算法记为HZDL; 文[9]中参数选取式(1.13)中的tk2时, 算法记为ADL6.为了检验算法2.1(NADL)的数值效果, 将算法HZDL, 算法ADL6和算法NADL在完全相同的强Wolfe线搜索下, 选取文[15]中的部分测试函数进行进行对比试验.所有算法程序都是用Matlab R2016a在CPU 3.20 GHz, RAM 4.0 GB, 操作系统为Windows 10的个人计算机上进行测试.参数选取为δ= 1e-4,σ= 0.8,ε= 1e-6, 终止条件为‖gk‖∞＜ε(1+|f(xk)|).数值结果见表4.1, 其中N表示测试函数序号, Function表示测试函数名称, NI表示迭代次数,FE表示目标函数值计算次数, GE表示目标函数的梯度计算次数, TCPU表示迭代时间(秒),NaN表示运行无结果.

表4.1 算法HZDL、算法ADL6和算法NADL的数值结果

根据表4.1中的数值结果分析, 除测试函数SING和SINGX, 我们提出的算法NADL对于其他测试函数是可行的; 对于测试函数ROSE, FROTH, BARD, BD, OSB2, ROSEX, PEN2,BV, IE以及TRID, 从迭代次数, 函数值计算次数, 梯度计算次数和迭代时间四个维度对比分析, 算法NADL明显优于另外两种算法.利用Dolan和Mor[16]提出的性能曲线, 图4.1和图4.2分别针对不同测试函数求解的迭代次数, 目标函数值与梯度值的总计算次数直观分析算法的效果.从图4.1和图4.2可以直观看出, 算法NADL在总体的计算性能上是优于算法HZDL和算法ADL6.

图4.1 基于迭代次数的性能概况

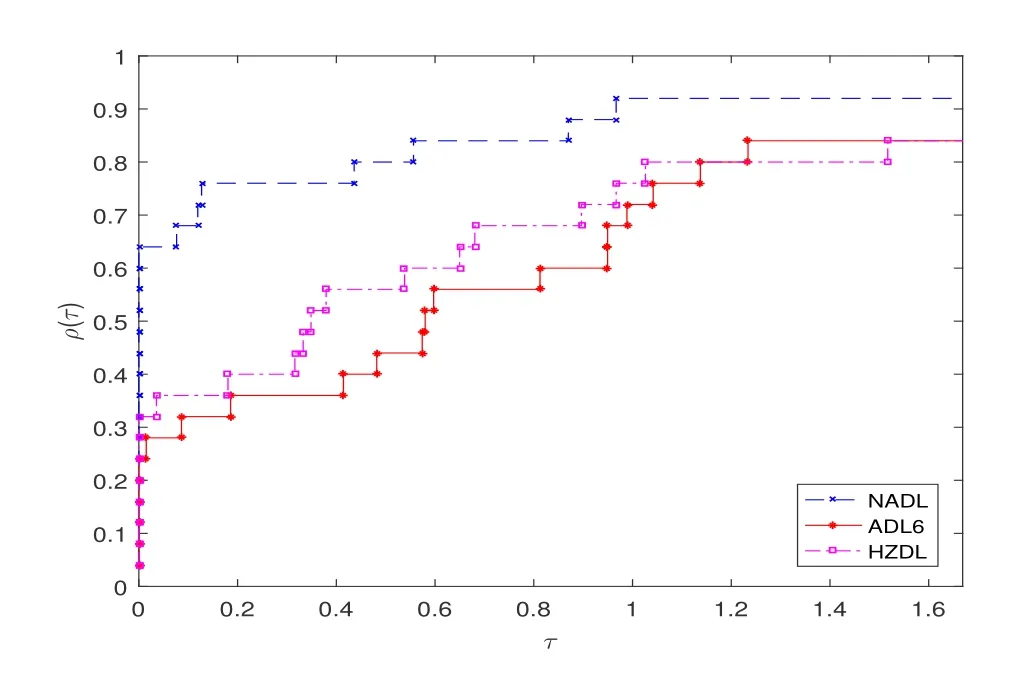
图4.2 基于函数值和梯度值的总计算次数的性能概况