带临界指数传输问题解的存在性研究
王跃, 钟荣花, 郝雪妍, 魏其萍
(1.贵州大学数学与统计学院, 贵州 贵阳 550025;2.天津财经大学管理工程与科学学院, 天津 300222;3.贵州民族大学数据科学与信息工程学院, 贵州 贵阳 550025)
1.引言和主要结论
传输问题在工程制造等行业中始终或多或少困扰着人们, 在工业制作中, 人工搬运下偶然因素较多, 例如工人体力支撑有限以及观察存在盲区等外界影响, 时效性得不到保证, 解决这一系列问题的过程促进了流水线的产生.流水线型工业生产中, 传送带在转运传输过程中起着不可忽视的作用, 由于传送带运行时往往会发生振动, 传送带上的材料时常会因为传送带的振动而发生掉落, 为了更好地解决该问题, 不得不对传送带本身的振动作相关研究, 如果已经充分了解传送带的振动状态, 便可以对症下药, 利用其他因素控制振动带来的负面影响.
振动问题的数学描述, 需要追溯到达朗贝尔和欧拉提出的波动方程和弦振动方程, 此后的研究中, 当不同外力和源项作用使f(t,x,u)≡0时Kirchhoff[1]提出了如下引人注目的振动模型:

其中v为无量纲化的传送带速度,vT >0是与匀速度相关的正常量.从方程自身来看, 传送带边界振动问题于Kirchhoff型问题而言其非局部系数中模量为负.我们通过文献查阅发现有这样的事实: 当两个原子靠得很近时表现出排斥力而离得远时表现出吸引力, 粮食供需等关系中的劲度系数有时为正有时为负等, 此中所表现出的便是负模量, 文[6]立足于该事实考虑了带有临界指数的负模量Kirchhoff问题后, 许多关于负模量Kirchhoff型数学问题解的存在性研究也沿用文[6]所叙述的物理意义.文[7]中对v进行了必要的说明, 0<v <1时是常态的转速,v= 1时是临界速度, 达到临界速度后振动将变得极不稳定, 就算带片自身的固有振动频率可以忽略不计, 都随时可能会产生不可估计的负面问题.例如, 交流电驱动下的传送带中, 常态速度下带片的速度大约等价于电动机的转速, 交流电一旦不稳定, 这个等价就失去平衡.如果电流过大, 电动机转速将提高, 其自身转子与传送带之间的摩擦力将随着转动速度而发生变化, 这将导致传送带的速度与电动机转速不匹配(一般小于电动机转速), 一旦传送带的速度v >1, 那么一方面会导致传送带上的材料颠簸而带来严重的负面影响, 另一方面也可能损坏电动机.为了保证流水线正常运作, 预防负面问题的发生, 需要添加适当的设备f(x,u)0以使得控制振动在一定的频率范围内, 其中f(x,u)的系数1表示抑制作用, 系数-1表示促进作用.由于在某些问题中所需要的结果可能与这里的相反, 例如需要振动频率越高越好, 因此是抑制还是促进需要根据实际出发.
设f(x,u)=λg(x)u3, 下面推广抑制作用的传输问题到高维, 即考虑带权函数的问题:


注记1定理1中, 由于临界值向上递增, 解序列{um}所对应的泛函值最后将趋于
2.预备知识

则直接可以证明I可微并且I的临界点就是问题(1.1)的解.

为了运用山路引理和对称山路引理[16]证明本文的结论, 现将其满足的条件列出如下:
引理1[16]设E是可分的实Banach 空间,I ∈C1(E,R)满足I(0)=0, 给出假设:
(I1)存在常数r,α >0使得对任意的u ∈Br{0}有I(u)>0; 对任意的u ∈Sr有I(u)≥α >0;
(I2) 存在函数e ∈E,0, 满足I(e)≤0;
(I3) 存在常数M >0, 使得同时满足的任意序列{un}⊂E有收敛子列;

(i) 记Γ={h ∈C([0,1],E)|h(0)=0,h(1)=e}, 如果条件(I1)-(I3)成立, 则
21世纪初,由Operstein提出了以植被覆盖来增强边坡稳定性,相对于传统土钉墙法,植被覆盖能完美地达到稳定边坡和美化环境的双赢效果。

是I的一个临界值且满足0<α ≤c <M.
记Γ={h ∈C(E,E)|h是E到E的同胚映射且h(Br)∈A0}, 则:
(ii) 如果h(τ)分离0和e, 那么满足条件(I1)-(I3)时,
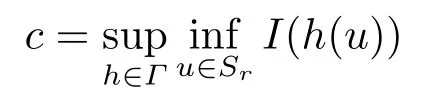
是I的一个临界值且满足0<α ≤c <M;
(iii) 如果h是奇映射, 那么满足条件(I1)和(I3)-(I5)时, 对每一个i ∈N*,
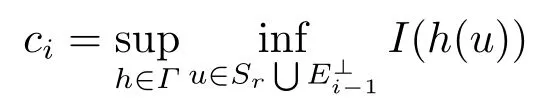
是I的一个临界值且满足0<α ≤ci ≤ci+1<M.由此推导出I有无穷多对临界点;
(iv) 如果h是奇映射且则(I3)-(I6)成立时对每个k >i,

通常, 结论(i)叫做山路引理, 结论(ii)-(iv)叫做对称山路引理.
3.定理1的证明
下面将对所考虑的问题进行逐项检验, 并与对称山路引理成立的条件作比较, 以此来证明次临界情形下问题(1.1) 无穷多解的存在性.


对上述的两式进行适当比较可得出
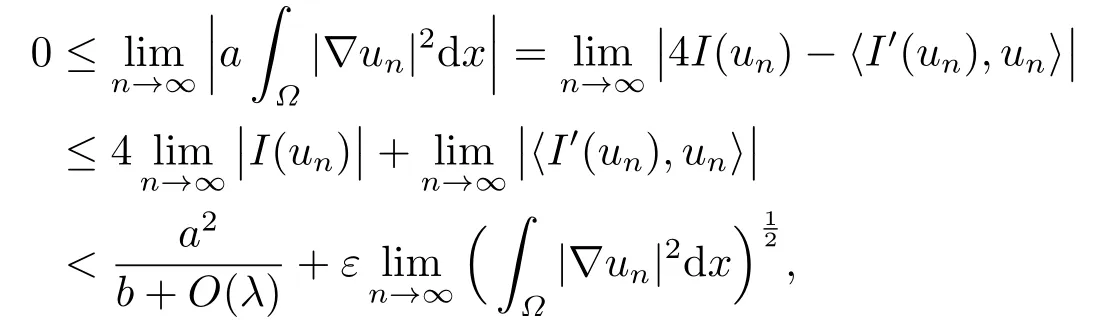

第四步 验证条件(I5)-(I6).事实上, 取Ei=Hi, 则条件(I5)-(I6) 都成立.

4.定理2的证明
由定理1的证明过程可见, 山路引理和对称山路引理的前提条件和(I1)-(I2)以及(I4)对N=4同样成立, 但当N= 4时Sobolev不等式嵌入不紧, 而且在RN上的达到函数不能张成整个空间, 从而空间分解失去作用.下面我们将证明当N=4时对称山路引理的条件(I3)也成立, 即证明所谓的(PS)c条件, 从而可以用山路引理证明方程(1.1)解的存在性.

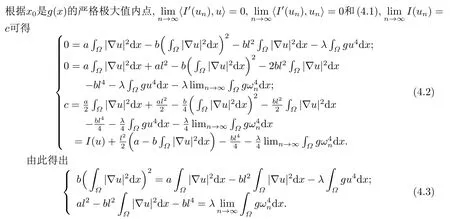
由于数列极限具有保号性, 从而根据(4.3)式和Sobolev嵌入不等式可得出可得

因此l2=0, 若不然就有

由此推出

一方面, 从(4.2)式以及(4.3)式的最后一个式子可得出
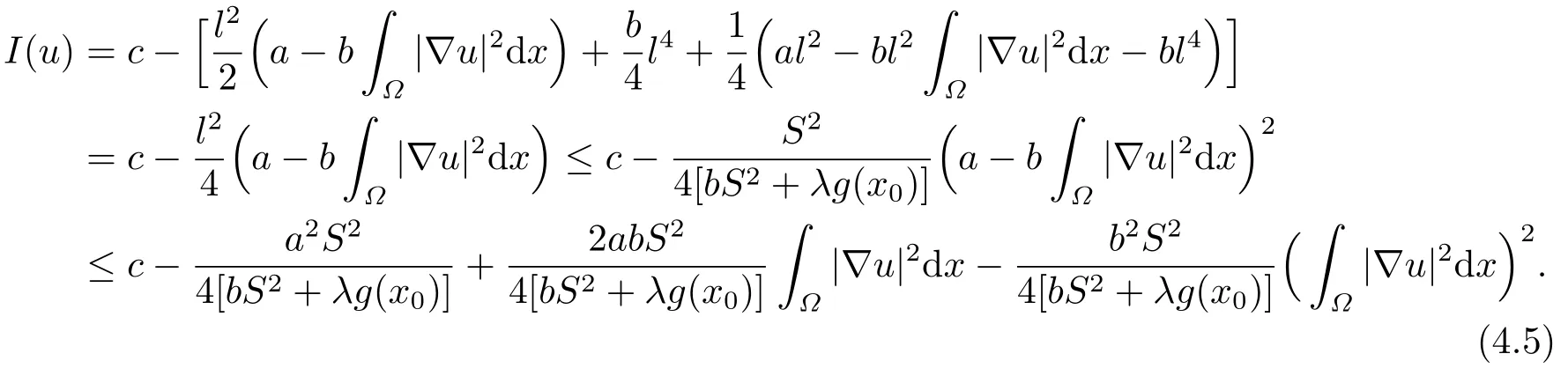
另一方面, 结合(4.3)式和(4.4)式知
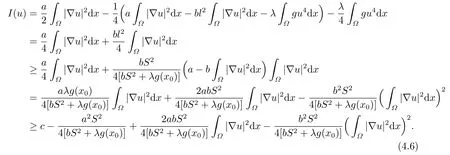

可达到, 从而根据山路引理,c是I的一个临界值且满足0<α ≤c <M.
证I的Nehari流形表示为
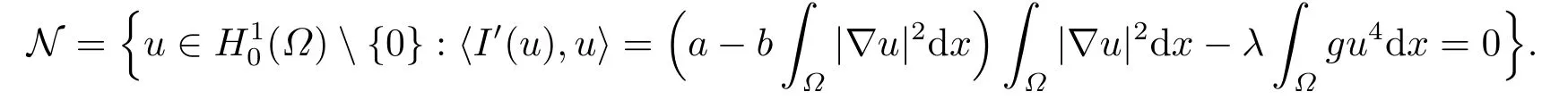
如果u是问题(1.1)的非平凡解, 则u ∈N.因此, 变分问题通常对应可以在Nehari流形上考虑,对问题(1.1)而言, 便是在N上考虑泛函I的极小值点, 既考虑极小化问题


根据引理3, 便得到了临界值c可以达到, 也就是说, 再联系到泛函的偶性便存在相应的一正一负两个临界点.从而说明当N=4时问题(1.1)至少存在一正一负两个解,根据c的达到可知此时的解是定义在g(x)的一个极大值点x0的邻域内, 因此推知当g(x)有k个极大值相等的严格极大值内点xi(i= 1,··· ,k)时问题(1.1)至少存在k个正解和k个负解.这便是推论2和推论3的主要结论.另外, 当g(x)的极小值点趋近于0时, 根据g(x)的连续性可知极小值点附近g(x)也趋近于0, 再根据引理3可知问题(1.1)对应的泛函值趋近于
——“模型类”相关试题选登
- 应用数学的其它文章
- 不确定离散时间输入饱和系统的鲁棒预见控制
- Maximal Operator of (C,α)-Means of Walsh-Fourier Series on Hardy Spaces with Variable Exponents
- Empirical Likehood for Linear Models with Random Designs Under Strong Mixing Samples
- 带分数阶边值条件的差分方程组的正解问题
- An Interior Bundle Method for Solving Equilibrium Problems
- 纵向数据下非参数带测量误差的部分线性变系数模型的估计

