基于6种不同行走状态下步幅特征对3种体态特征推定的研究
史洪飞,魏晓辉,蒋 敬,徐伯芃
(1.南京森林警察学院,江苏南京 210023;2.国家林业局森林公安司法鉴定中心,江苏南京 210023;3.长江航运公安局安庆分局刑侦支队,安徽安庆 246000)
0 引言
足迹学作为痕迹学中一个有影响力的分支,是在国家法律机构与社会犯罪行为作斗争的过程中,为了提供有关证据的需要而产生的[1]。在犯罪案件现场,只要有作案人在现场活动,就有可能留下足迹。虽然与手印、DNA检材相比,足迹的提取率较低,但也达到了35%[2]。由于人们在成长的过程中受到不同因素的长期影响,使每个人在一定时期内形成相对稳定、不易改变、特征明显的独特的足迹步幅特征,并且在不同的行走状态下,个人的足迹步幅特征也存在一定的差异,因此对现场遗留的足迹进行分析,可以推断犯罪嫌疑人的生理活动特点,锁定犯罪嫌疑人,为侦查破案提供线索。
目前,足迹检验技术在原有的形象检验、步法检验的基础上,发展了鞋底磨损检验、足迹动力形态检验,并向足迹定量化检验等新领域进行研究,从基础理论到检验方法均已形成自己的特色,无论是检验对象、内容、方法与手段等都有了很大的发展与进步[3]。然而,国内、外关于足迹的研究主要集中在足迹的形态特征,对足迹步幅特征的研究存在一定的局限性。计算机技术的应用、统计学理论的发展标志着足迹检验技术已经开始从以个人经验为主观依据阶段向以仪器设备检验为客观依据的定量化检验阶段发展,将统计学与足迹学相结合,使足迹检验技术在侦查破案中[4]发挥更大作用。
本文运用SPSS数据分析软件中的Pearson相关分析和线性回归分析对步幅特征参数进行统计分析,总结6种行走状态下的赤足足迹之间的步幅特征关系[5],根据步幅特征参数的相关性和线性回归方程,推断犯罪嫌疑人遗留下来的在6种行走状态下赤足足迹是否为伪装足迹[6];推断遗留足迹的犯罪嫌疑人的3种体态特征,锁定犯罪嫌疑人,为诉讼提供证据[7]。
1 实验方法
1.1 实验数据收集方法
(1)实验开始时先对每一位受试者,测量其身高、体重,再通过肥胖指数公式(肥胖指数=体重÷身高2)计算出肥胖指数;
(2)在海绵上涂抹油墨。将沾有油墨的油墨磙,从海绵的一端匀速地推向另一端,反复多次,使海绵上油墨分布均匀;
(3)铺开工程复印纸(长15 m),将实验对象的姓名、性别、身高、体重记录在工程复印纸上;
(4)捺印赤足平面-成趟足迹。首先赤脚立正站在海绵上,使左右两只脚底面均匀地沾附上油墨,同时注意足尖和足跟捺印完整,要求实验对象站立在工程复印纸上收集赤足足迹后,再要求实验对象依次按照正常行走、快速正常行走、快速大步行走、快速小步行走、慢速正常行走和倒退行走,从白纸的一侧向另一侧行走[8];
(5)分别量取实验对象在正常行走、快速正常行走、快速大步行走、快速小步行走、慢速正常行走和倒退行走状态下赤足成趟足迹的左步长、右步长、左步宽、右步宽、左步角、右步角并记录;
(6)设身高:H,单位:m;体重:W,单位:kg;肥胖指数:BMI,单位:kg/m2;左步长:Lp,单位:cm;右步长:Rp,单位:cm;左步宽:Lw,单位:cm;右步宽:Rw,单位:cm;左步角:La,单位:°;右步角:Ra,单位:°。
1.2 步幅特征参数测量方法
统一测量方法,测量实验对象在正常行走与快速正常行走状态下赤足成趟足迹的左步长、右步长、左步宽、右步宽、左步角、右步角,并记录。对左步长、右步长、左步宽、右步宽、左步角、右步角各测量5组数据,取平均值[9]。
(1)步行线的确定
选取同一只脚两个相邻的足迹内边缘的点,连线,作为步行线;
(2)足迹中心线的确定
连接足迹后跟中心点与足迹第二枚脚趾中心点,作为足迹中心线;
(3)步长的测量
从左足迹后跟边缘作左步行线的垂线,从相邻右足迹后跟边缘作左步行线的垂线,两条步行线垂线之间的距离为左步长;从右足迹后跟边缘作右步行线的垂线,从相邻左足迹后跟边缘作右步行线的垂线,两条步行线垂线之间的距离为右步长;
(4)步宽的测量
左足迹脚后跟内侧最凸点到右步行线的距离为左步宽;右足迹后脚跟内侧最凸点到左步行线的距离为右步宽;
(5)步角的测量
左足迹中心线与左步行线相交所形成的角为左步角;右足迹中心线与右步行线相交所形成的角为右步角。
1.3 实验数据分析方法
(1)相关分析
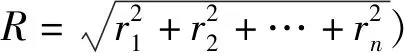
(2)线性回归分析
线性回归是确定两种或两种以上的变量间线性关系的一种分析方法[11]。在回归分析中,如果只包含一个自变量与一个因变量,二者的关系可用一条直线表示,则称为一元线性回归分析;如果包含两个以上的自变量,而且因变量和自变量间是线性关系,则称为多元线性回归分析。本文采用多元线性回归分析,利用SPSS确定身高、体重与6种行走状态下的步幅特征之间的线性关系。
2 实验结果与分析
2.1 实验数据
实验选取138名19~23岁成年人作为实验对象,其中男性108名,女性30名。对正常行走、快速正常、快速大步、快速小步、慢速正常、倒退6种行走状态下赤足足迹的左、右步长,左、右步宽,左、右步角等步幅特征参数进行测量,每种行走状态下的数据取行走过程的中间部分,并分别测量3次取平均值。
2.2 正常行走状态下步幅特征与3种体态特征的相关性分析及线性回归分析
2.2.1 正常行走状态下步幅特征与3种体态特征的相关性分析
根据表1,正常行走状态下赤足成趟足迹的左步长与体重呈正弱相关关系,r=0.249;左步长与身高呈正中等程度相关关系,r=0.492;右步长与体重呈正极弱相关关系,r=0.186;右步长与身高呈正弱相关关系,r=0.394;左步宽与体重呈正弱相关关系,r=0.268;左步宽与身高呈正极弱相关关系,r=0.185;左步宽与肥胖指数呈正弱相关关系,r=0.253;右步宽与体重呈正弱相关关系,r=0.244;右步宽与肥胖指数呈正弱相关关系,r=0.241;左步角与身高呈正极弱相关关系,r=0.220;右步角与身高呈正极弱相关关系,r=0.242。
所以身高的综合相关系数r综=0.751,为强相关;体重的综合相关系数r综=0.492,肥胖指数的综合相关系数为r综=0.367。
2.2.2 正常行走状态下步幅特征与3种体态特征的线性回归分析
(1)正常行走状态下步幅特征与身高线性回归分析
据表2,所有6个变量均进入模型,说明解释变量都是显著并且是有解释力的。
据表3,模型拟合优度系数为0.568,反映了因变量与自变量之间具有中度显著的线性关系,模型标准估计误差为0.056。
据表4,模型的设定检验F统计量的值为10.396,显著性水平Sig值几乎为零,因变量与自变量之间的线性关系明显。
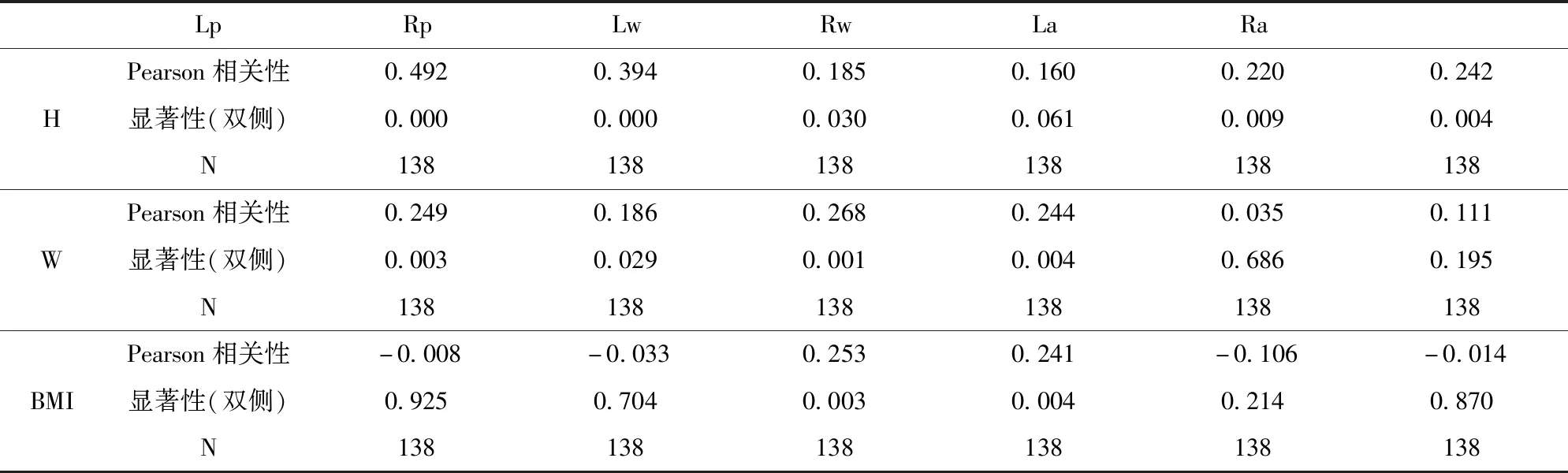
表1 体重、身高、肥胖指数与正常行走状态赤足成趟足迹各参数间的相关性数据表

表2 输入/移去的变量b

表3 模型汇总b
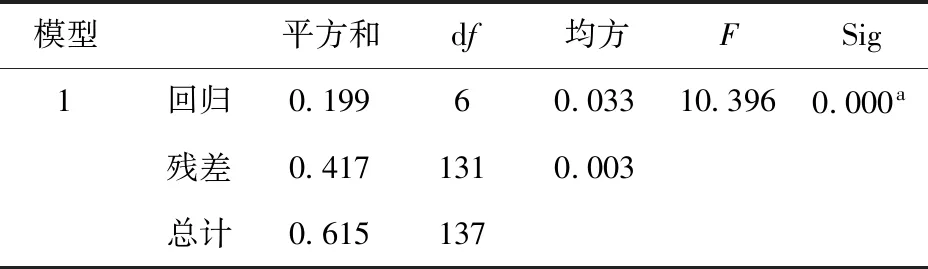
表4 方差分析表b
据表5、6,变量Rp、Rw、Ra的显著性检验的t值较小,未能通过变量的显著性检验,未达到显著性水平,因此将3个变量排除。所以正常行走状态下步幅特征与身高之间的线性关系如下:
H=1.379+0.005×Lp+0.002×La+0.005×Lw
回归方程建立后,正常行走状态下观测的(实际测量的)累积概率(横坐标)与期望的(根据回归方程计算的)累积概率(纵坐标)的正态概率图如图1所示。
(2)正常行走状态下步幅特征与体重线性回归分析
参照(1)可得出正常行走状态下步幅特征与体重之间的线性关系如下:
W=37.280+0.355×Lp+1.021×Lw

表5 相关性系数a
(3)正常行走状态下步幅特征与肥胖指数线性回归分析
参照(1)可得出正常行走状态下步幅特征与肥胖指数之间的线性关系如下:
BMI=21.235+0.143×Rw
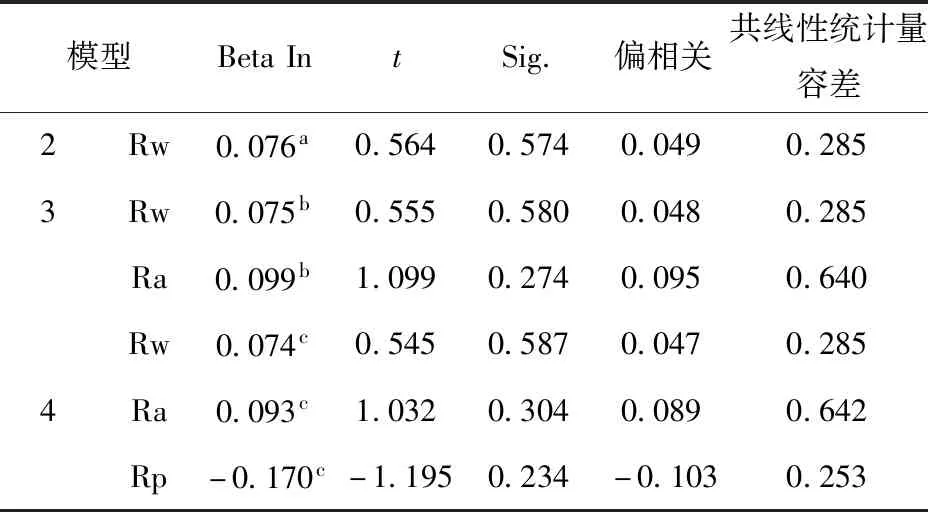
表6 已排除的变量d
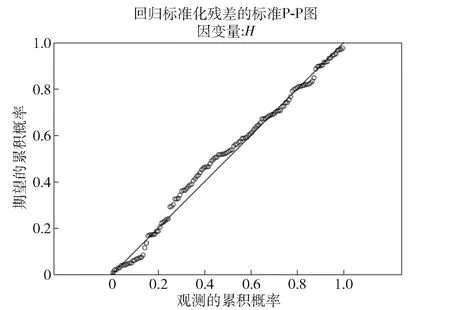
图1 正常行走状态下步幅特征与身高的正态概率图
2.3 快速正常行走状态下步幅特征与3种体态特征的相关性分析及线性回归分析
2.3.1 快速正常行走状态下步幅特征与3种体态特征的相关性分析
快速正常行走状态下赤足成趟足迹的左步长与体重呈正弱相关关系,r=0.243;左步长与身高呈正中等程度相关关系,r=0.475;右步长与体重呈正弱相关关系,r=0.213;右步长与身高呈正中等程度相关关系,r=0.437;左步宽与体重呈正弱相关关系,r=0.207;左步宽与肥胖指数呈正弱相关关系,r=0.183;右步宽与体重呈正极弱相关关系,r=0.174;右步宽与肥胖指数呈正极弱相关关系,r=0.189。
所以身高的综合相关系数r综=0.696,为强相关;体重的综合相关系数r综=0.425,为中度相关;肥胖指数的综合相关系数r综=0.272,为弱相关。
2.3.2 快速正常行走状态下步幅特征与3种体态特征的线性回归分析
参照(1)可得出快速正常行走状态下步幅特征与身高之间的线性关系为:
H=1.430+0.004×Lp+0.001×La+0.009×Lw-0.006×Rw
快速正常行走状态下步幅特征与体重之间的线性关系为:
W=42.192+0.301×Lp+0.536×Lw
所以快速正常行走状态下步幅特征与肥胖指数之间的线性关系为:
BMI=20.449+0.078×Ra+0.193×Lw
2.4 快速大步行走状态下步幅特征与3种体态特征的相关性分析及线性回归分析
2.4.1 快速大步行走状态下步幅特征与3种体态特征的相关性分析
快速大步行走状态下赤足成趟足迹的左步长与体重呈正弱相关关系,r=0.326;左步长与身高呈正中等程度相关关系,r=0.462;右步长与体重呈正弱相关关系,r=0.213;右步长与身高呈正中等程度相关关系,r=0.401;右步角与体重呈正弱相关关系,r=0.232。
所以身高的综合相关系数r综=0.695,为强相关;体重的综合相关系数r综=0.534,为中度相关;肥胖指数的综合相关系数r综=0.318,为弱相关。
2.4.2 快速大步行走状态下步幅特征与3种体态特征的线性回归分析
参照(1)可得出快速大步行走状态下步幅特征与身高之间的线性关系为:
H=137.175+0.388×Lp+0.162×Ra+0.505×Rw
快速大步行走状态下步幅特征与体重之间的线性关系为:
W=27.183+0.418×Lp+0.693×Rw
快速大步行走状态下步幅特征与肥胖指数之间的线性关系为:
BMI=21.580+0.103×Rw
2.5 快速小步行走状态下步幅特征与3种体态特征的相关性分析及线性回归分析
2.5.1 快速小步行走状态下步幅特征与3种体态特征的相关性分析
快速小步行走状态下赤足成趟足迹的左步长与身高呈正弱相关关系,r=0.327;右步长与身高呈正弱等程度相关关系,r=0.306;左步角与身高呈正弱相关关系,r=0.295;右步角与身高呈正弱等程度相关关系,r=0.226;左步角与体重呈正弱相关关系,r=0.223。
所以身高的综合相关系数r综=0.643,为强相关;体重的综合相关系数r综=0.493,为中度相关;肥胖指数的综合相关系数为r综=0.383,为弱相关。
2.5.2 快速小步步行走状态下步幅特征与3种体态特征的线性回归分析
参照(1)可得出快速小步行走状态下步幅特征与身高之间的线性关系
H=1.500+0.003×Lp+0.003×La+0.006×Lw
快速小步行走状态下步幅特征与体重之间的线性关系
W=43.066+0.234×Lp+0.433×Ra+1.041×Lw
快速小步行走状态下步幅特征与肥胖指数之间的线性关系
BMI=22.391+0.093×Lp-0.104×Rp+0.096×Rw
2.6 慢速正常行走状态下步幅特征与3种体态特征的相关性分析及线性回归分析
2.6.1 慢速正常行走状态下步幅特征与3种体态特征的相关性分析
慢速正常行走状态下赤足成趟足迹的左步长与身高呈正弱相关关系,r=0.303;右步长与身高呈正弱等程度相关关系,r=0.246。
所以身高的综合相关系数r综=0.476,为中度相关;体重的综合相关系数r综=0.318,为弱相关;肥胖指数的综合相关系数r综=0.268,为弱相关。
2.6.2 慢速正常步行走状态下步幅特征与3种体态特征的线性回归分析
参照(1)可得出慢速正常行走状态下步幅特征与身高之间的线性关系为:
H=1.543+0.002×Lp+0.003×La+0.003×Lw
慢速正常行走状态下步幅特征与体重之间的线性关系为:
W=54.79+0.557×Lp-0.401×Rp+0.503×Lw
慢速正常行走状态下步幅特征与肥胖指数之间的线性关系为:
BMI=21.042+0.218×Lw
2.7 倒退行走状态下步幅特征与3种体态特征的相关性分析及线性回归分析
2.7.1 倒退行走状态下步幅特征与3种体态特征的相关性分析
在倒退行走状态下,身高与赤足足迹的左步长、右步长呈正相关关系,相关系数分别为r=0.269弱相关和r=0.331弱相关;在倒退行走状态下,体重与赤足足迹的右步长呈正相关关系,相关系数为r=0.233弱相关;个人在倒退行走状态下,肥胖指数与赤足足迹的左步宽、右步宽呈正相关关系,相关系数分别为r=0.220弱相关和r=0.193极弱相关。
所以身高的综合相关系数r综=0.476,为中度相关;体重的综合相关系数r综=0.425,为中度相关;肥胖指数的综合相关系数r综=0.329,为中度相关。
2.7.2 倒退行走状态下步幅特征与3种体态特征的线性回归分析
参照(1)可得出倒退行走状态下步幅特征与身高之间的线性关系为:
H=1.598+0.003×Rp+0.001×La
倒退行走状态下步幅特征与体重之间的线性关系为:
W=52.205+0.257×Lp+0.322×Lw
倒退行走状态下步幅特征与肥胖指数之间的线性关系为:
BMI=21.379+0.093×Lw
2.8 6种行走状态下步幅特征与3种体态特征的综合相关性研究
表中身高、体重、肥胖系数和之前的不一致,之前为H、W、BMI。
根据表7,计算出平均综合相关性,身高平均综合相关系数为R=0.623,具有强相关性;体重平均综合相关系数为R=0.448,具有中度相关性;肥胖指数平均综合相关系数为R=0.323,具有弱相关性。
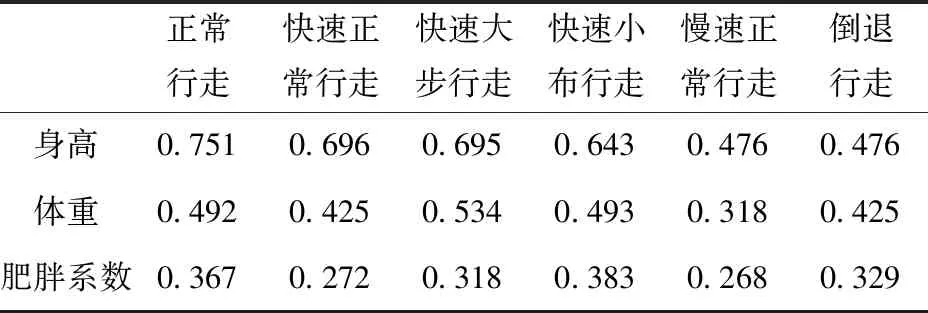
表7 综合相关数据表
2.9 步幅特征与3种体态特征线性关系的推导
步幅特征与身高的线性关系
快速大步行走状态下:
H=1.372+0.004×Lp+0.002×Ra+0.005×Rw
①
快速小步行走状态下:
H=1.500+0.003×Lp+0.003×La+0.006×Lw
②
快速正常行走状态下:
H=1.430+0.004×Lp+0.001×La+
0.009×Lw-0.006×Rw
③
慢速正常行走状态下:
H=1.543+0.002×Lp+0.003×La+0.003×Lw
④
正常行走状态下:
H=1.379+0.005×Lp+0.002×La+0.005×Lw
⑤
倒行状态下:
H=1.598+0.003×Rp+0.001×La
⑥
式②-式③得到:
0=0.070-0.001×Lp+0.002×La-0.003×Lw+0.006×Rw
⑦
式④-式⑤得到:
0=0.160-0.002×Lp+0.009×La-0.002×Lw
⑧
式⑦-式⑧得到:
0=-0.090+0.001×Lp+0.001×La+
0.001×Lw+0.006×Rw
⑨
式①+式⑥得到:
H=1.485+0.002×Lp+0.001×Rp+
0.001×La+0.001×Ra+0.002×Rw
⑩
H=1.579+0.001×Lp+0.001×Rp+
0.001×Ra+0.001×Lw-0.004×Rw
同理可推算出:
W=23.058+0.478×Lp-0.272 5×Rp-1.249×Lw+0.346 5×Rw
BMI=23.787+0.093×Lp-0.104×Rp-0.364 5×Lw+0.270 5×Rw-0.078×Ra
3 步幅特征与3种体态特征的综合相关性线性关系的实践验证
3.1 平均综合相关性实践验证
另取15人,测量并汇总其体态特征及在6种行走状态下的步幅特征,利用SPSS得出相关性数据验证结果,如表8所示。
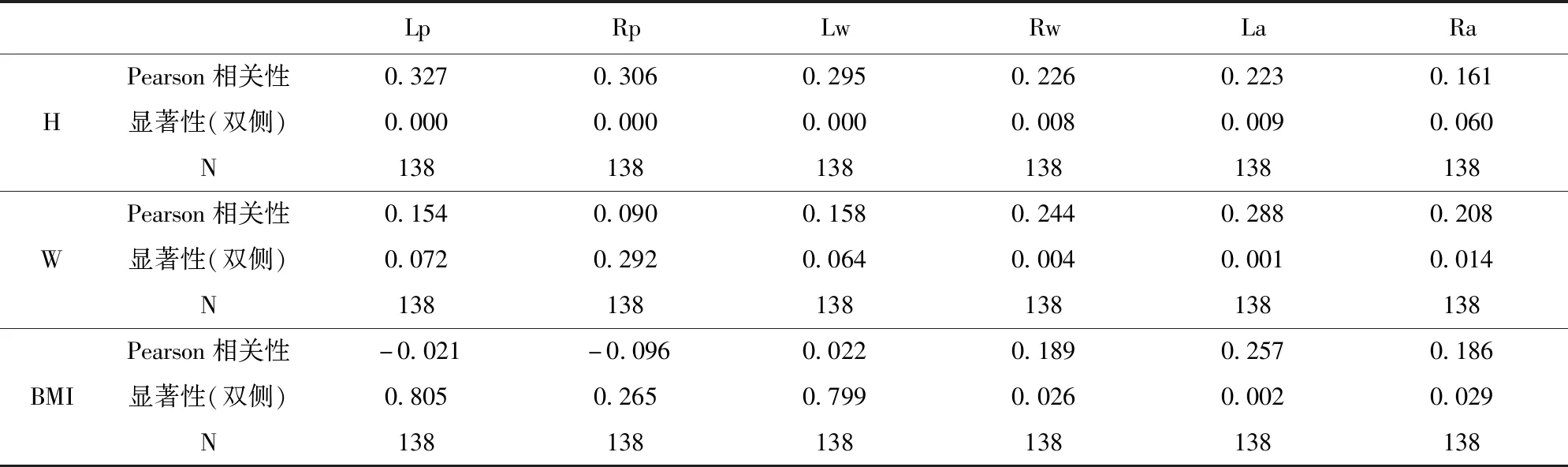
表8 体重、身高、肥胖指数与快速小步行走状态赤足成趟足迹各参数间的相关性数据表
根据表8可得身高的综合相关系数r综=0.643,为强相关;体重的综合相关系数r综=0.493,为中度相关;肥胖指数的综合相关系数为r综=0.383,为弱相关。与平均综合相关性偏差较小,故平均综合相关性可采信。
3.2 步幅特征与3种体态特征线性关系的实践验证
偏差率公式为
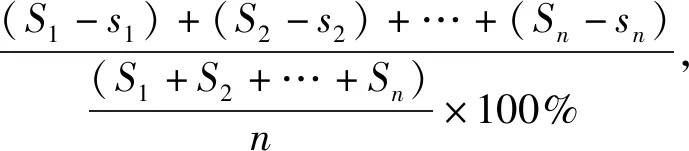
身高根据总公式利用步幅特征计算的身高与实际的身高的偏差率为0.64%,体重根据总公式利用步幅特征计算的体重与实际体重的偏差率为1.26%,肥胖指数根据总公式利用步幅特征计算的肥胖指数与实际的肥胖指数偏差率为1.50%。
4 讨论
(1)统计学理论的应用需要结合大量的实验样本,在本实验中样本的选取均来自于南京森林警察学院的学生,实验样本有限且男性与女性数量差距大,存在一定的局限性,得出的实验结果也具有一定的片面性。因此,需要进一步进行大量的样本试验,完善的实验结果。
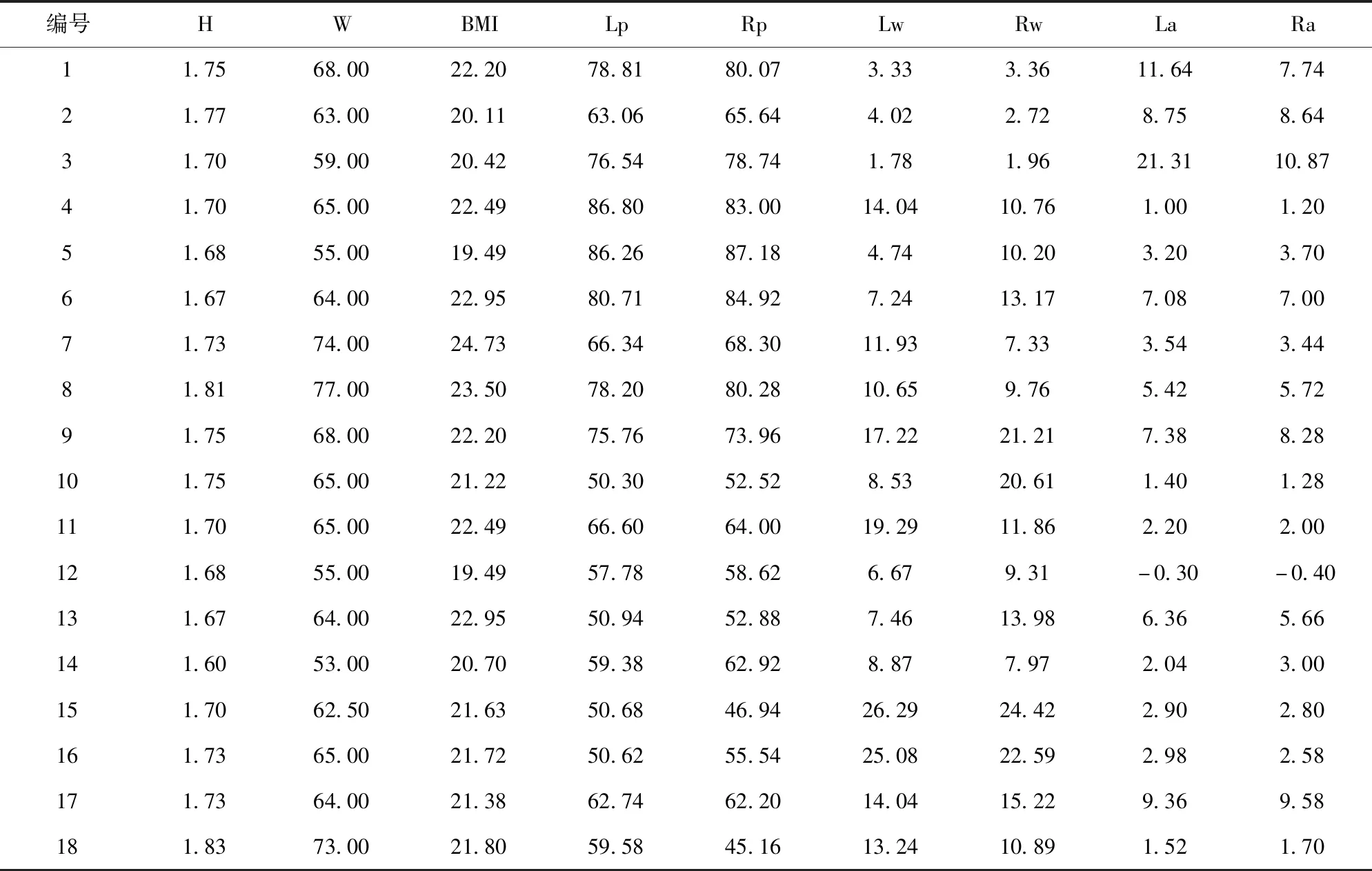
表9 抽取验证数据表
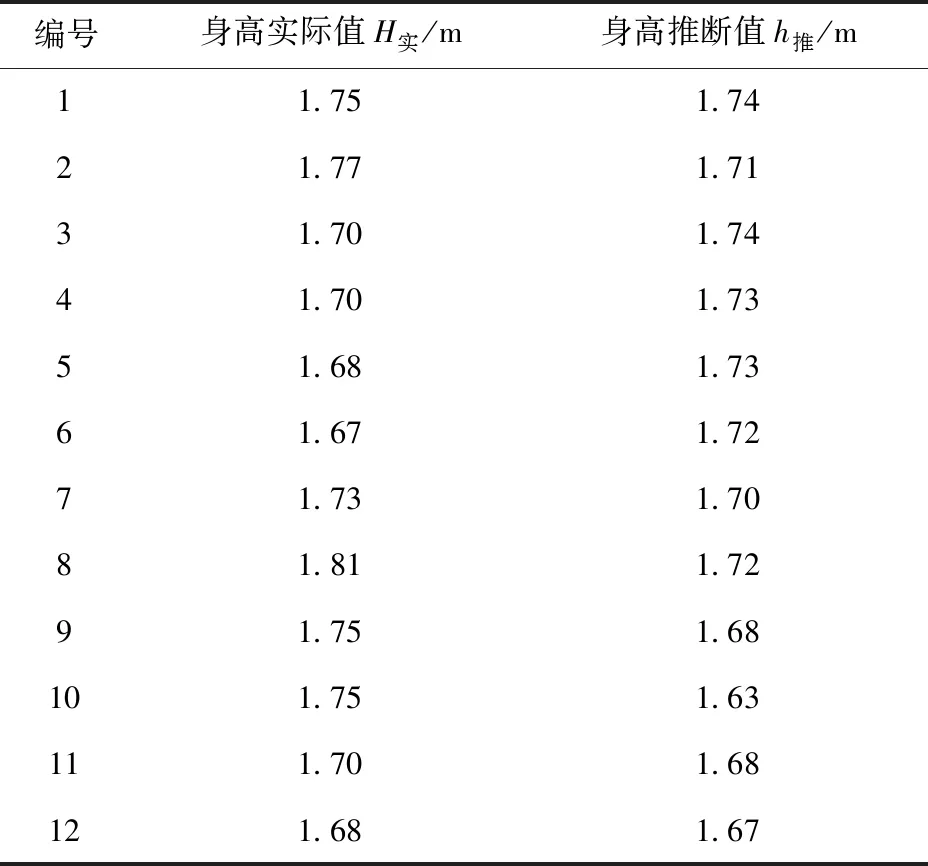
表10 身高总公式验证表
(2)在计算综合相关性时利用到欧式距离分析法,但是由于技术手段等原因,未能计算其矢量性。
(3)在实验数据测量中,由于器材的选取不够精确,导致测量的数据存在误差,从而影响到实验结果。因此,实验器材对实验结果的影响有待于进一步研究。
身高根据总公式利用步幅特征计算的身高与实际的身高的偏差率为0.64%,体重根据总公式利用步幅特征计算的体重与实际体重的偏差率为1.26%,肥胖指数根据总公式利用步幅特征计算的肥胖指数与实际的肥胖指数偏差率为1.50%。
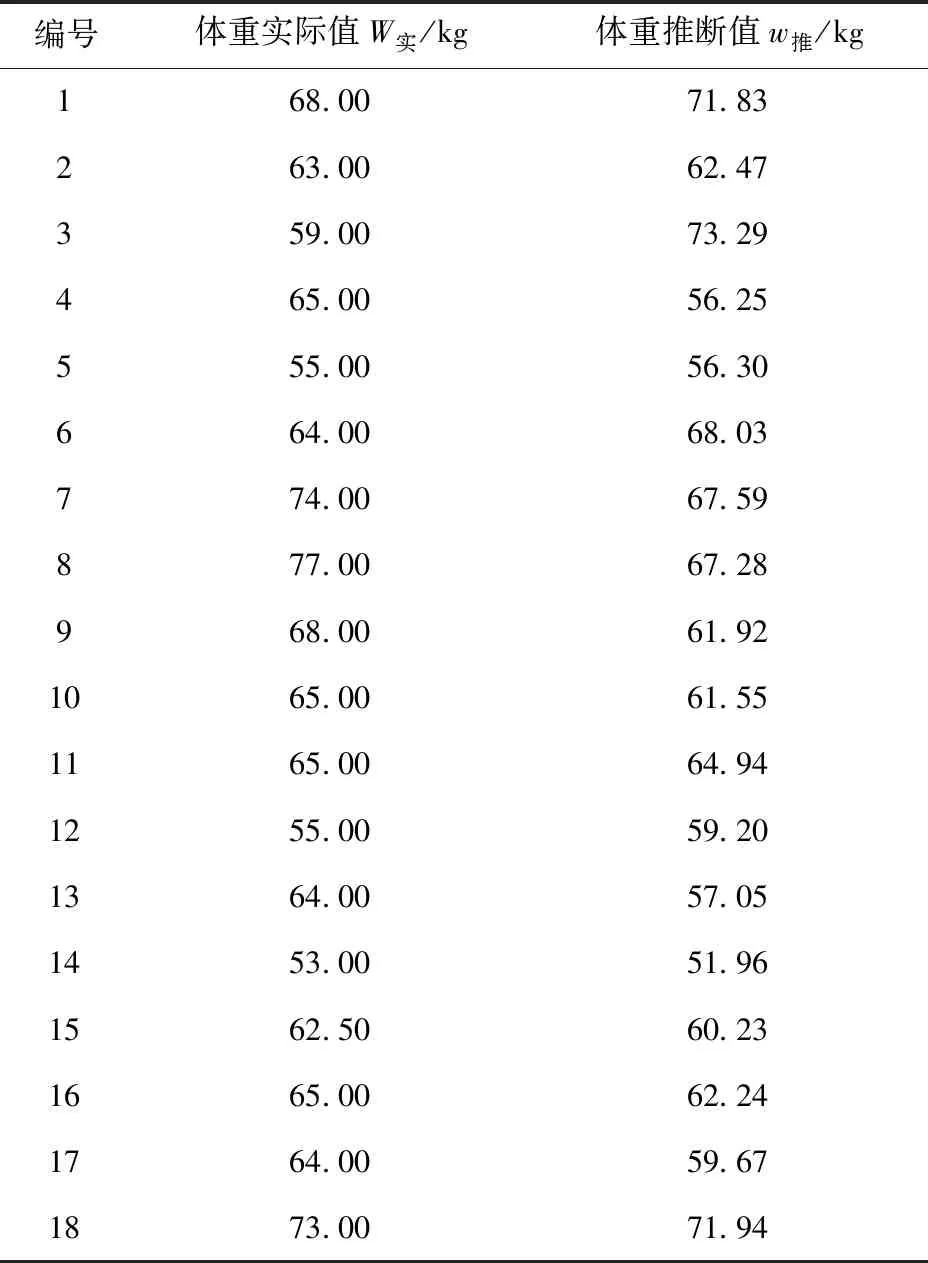
表11 体重总公式验证表
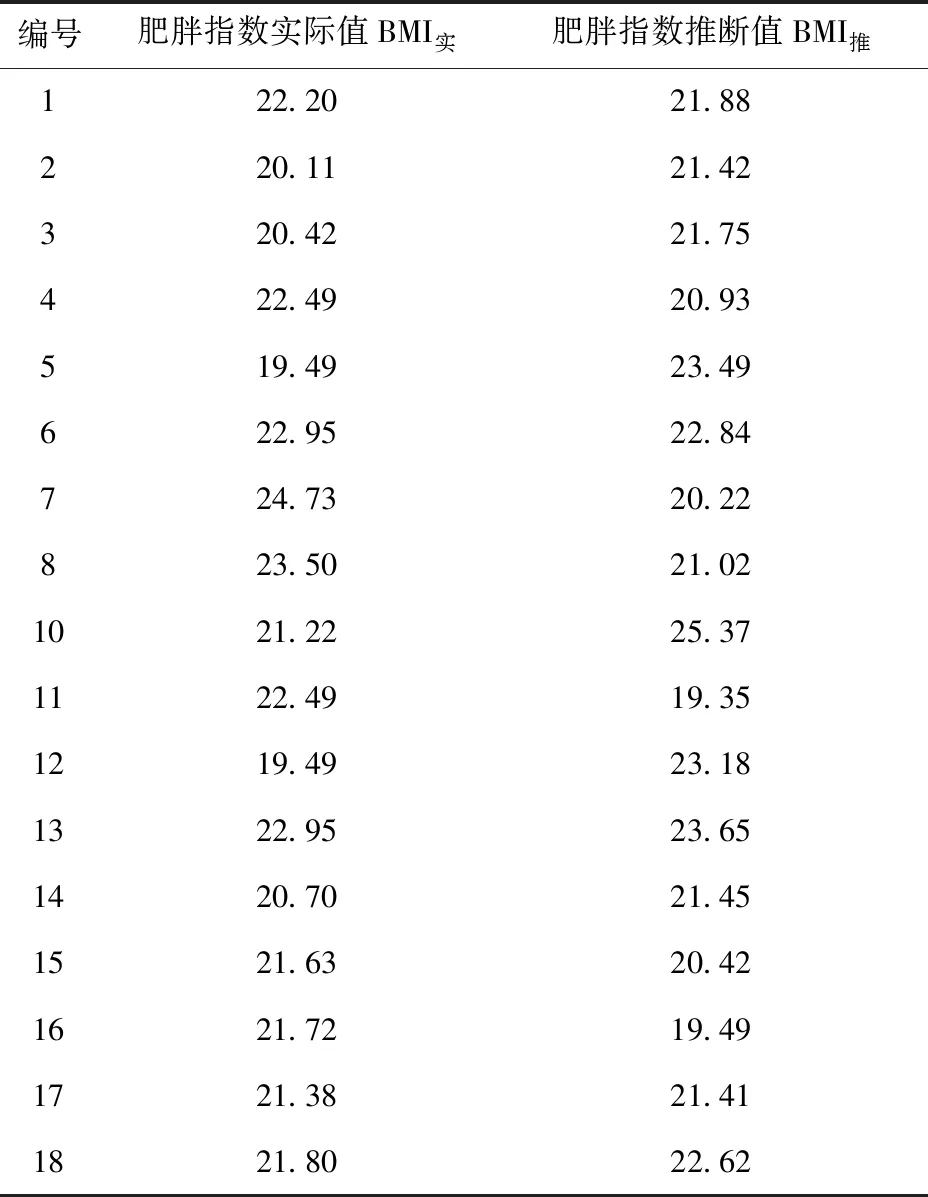
表12 肥胖指数总公式验证表
5 结语
本文综合考虑了6种行走状态下的步幅的数量特征与身高、体重和肥胖指数的相关关系及线性关系,并结合距离分析提出了综合相关性的检验问题,在数据分析的基础上建立了基于步幅特征推断身高、体重和肥胖指数的公式,并对各公式进行了实际验证;利用推导出的公式可较为准确的推断人的身高、体重和肥胖指数,推进了足迹步幅特征检验的量化研究,为后续足迹检验乃至痕迹检验的量化研究提供了借鉴,推进了痕迹检验的量化研究。实践案件中,步幅特征的研究及实践应用,计算机及大数据的应用将进一步推进足迹步幅特征的研究。

