一类带Logistic源项的趋化方程组解的定性性质
蒋 科,林小汇,夏安银
(西华大学 理学院,四川 成都 610039)
1 序言及预备知识
趋化性是指细胞受到空间中分布不均匀的物质所产生的化学信号的刺激而产生的定向运动.它分为两类:趋化吸引意味着细胞向信号浓度增加的方向移动,趋化排斥意味着细胞向信号浓度降低的方向移动.趋化性在免疫系统反应、胚胎发育、肿瘤生长等生物学现象中起着重要作用.20 世纪70 年代,Keller和Segel[1]根据细胞黏菌的趋化现象提出了标准的Keller-Segel模型:

其中未知函数u(x,t)、v(x,t)分别表示细胞密度和化学信号浓度.由第2 个方程可知,细胞既消耗化学物质,又会产生化学物质.考虑方程组的齐次Neumann初边值问题,即考虑模型:

其中Ω⊂Rn(n∈N)是一个具有光滑边界的有界区域,ν 是边界∂Ω 的单位外法向量.文献[2-4]证明了空间维数n =1 时,对任意充分光滑的初值,模型(1)存在全局有界经典解;当n =2,初值充分小时,同样存在全局有界经典解;当n≥3 时,对任意小的初值,模型(1)的解在有限时刻爆破.
由于不同生物环境中的趋化机制不同,许多学者开始关注经典Keller-Segel 模型的各种变体,其中一类为如下只含信号消耗而没有产生机制的模型:
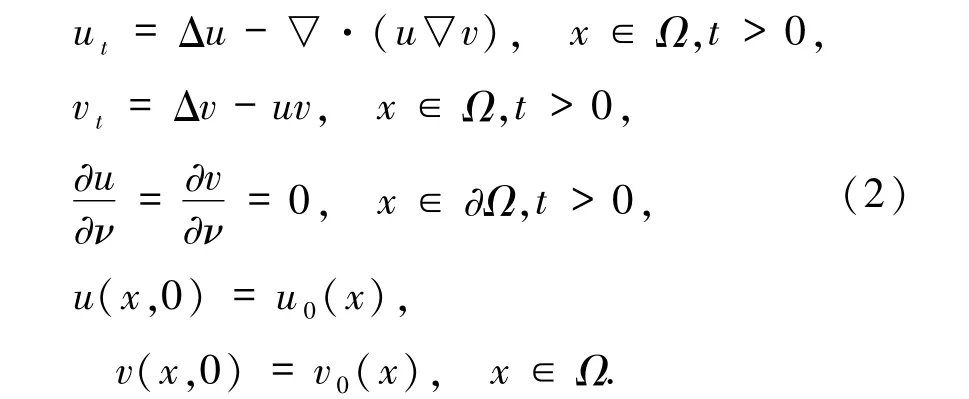
此模型的第2 个方程表明氧气在与细菌接触后以固定的速率降解,并且不再产生额外的氧气.针对此模型,如果考虑有界凸区域,文献[5-6]对解的适定性问题做了大量的工作.
在大时间尺度下,细菌自身的增殖与死亡也应该被考虑.Mimura等[7]研究了基于细菌趋化、扩散和增长的模型.他们在模型(1)中增加了Logistic源项ru-μu2(r≥0,μ >0).后续的研究表明,Logistic源项对方程组解的爆破有一定的抑制作用.
Winkler[8]研究了一类含Logistic 源项的趋化模型:
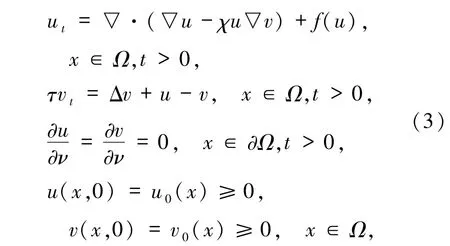
其中Ω⊂Rn(n∈N)是一个具有光滑边界的有界凸区域,τ >0.f(u)是Logistic 增长项且f(0)≥0,k≥0,μ >0 及

当μ足够大时,作者证明了模型(3)存在全局有界经典解.Wang等[9]考虑以下具有Logistic源项的趋化模型:
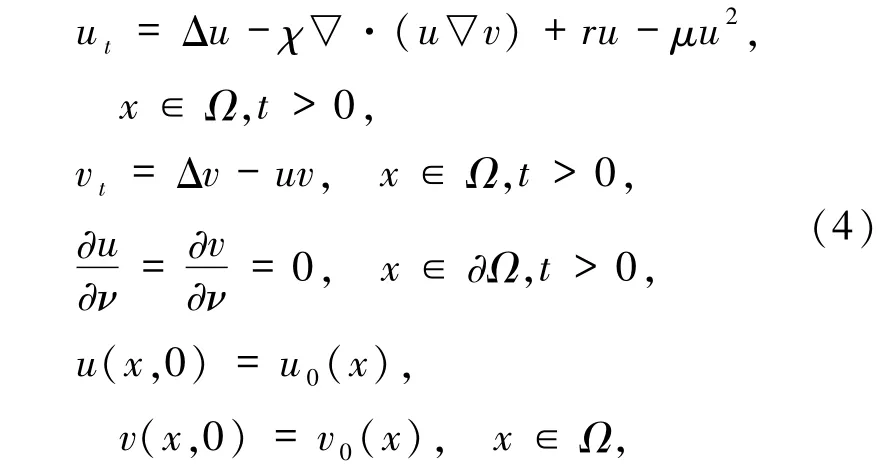
证明了对于适当大的μ >0,模型(4)存在全局经典解;对任意的μ >0,模型(4)存在全局弱解.关于更多带Logistic 源项的Keller-Segel 模型的变体以及相关结论,可参看文献[10-13].
自经典的Keller-Segel 模型及一些变体模型以后,关于趋化方程组的已有研究大多集中在对其整体适定性及长时间渐进行为等性质的研究,但是对方程组解自身定性性质的研究,还明显不足.最近,文献[14]证明了模型(3)在任意空间维数上其解都有一个正的下界,这表明如果细胞有任何死亡现象,那么它一定是空间上的局部性质,整个细胞种群总是持续存在的.
受到这项工作的启发,考虑这种细胞的持续存在性是否仍然适用于只含消耗机制的趋化模型(4).对于模型(3)而言,信号产生机制对质量的持续存在性有积极的影响.但是模型(4)只含信号消耗机制.因此,对于任何给定的时间尺度,它是否仍然具有类似的性质是一个有趣的问题.更确切地说,考虑
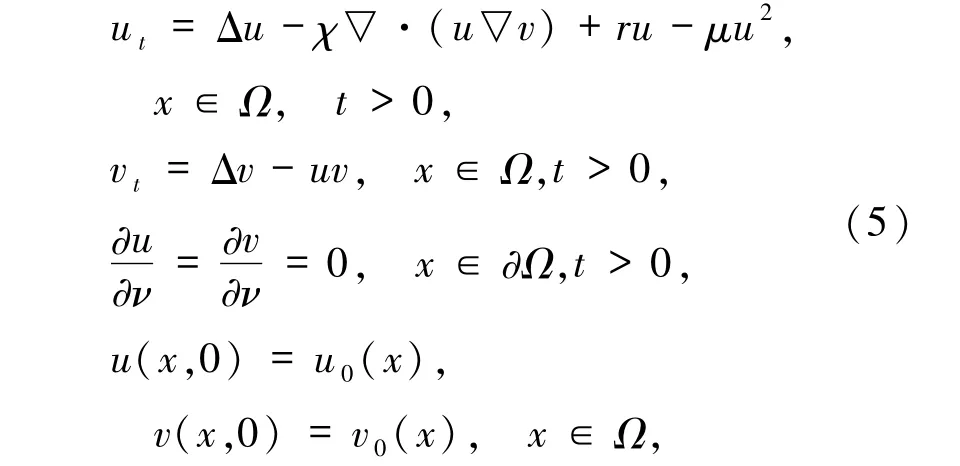
其中Ω⊂Rn(n∈N)是一个具有光滑边界的有界区域,r,χ,μ >0.假设初始条件满足:
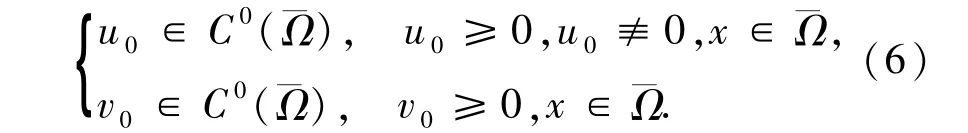
在这样的初始条件假设下,根据文献[9]可知,存在正常数k1(n)、k2(n),使得当
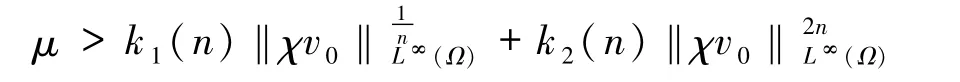
时,方程组(5)存在全局有界经典解(u,v).基于这一全局存在性和有界性的结果,将继续对模型(5)的解进行定性性质的研究.
为行文方便,令
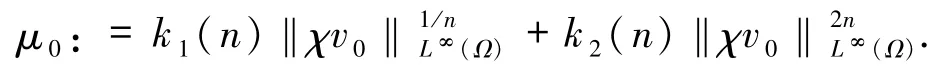
定理1.1假设Ω⊂Rn(n∈N)是一个具有光滑边界的有界区域,且χ,r,μ >0.若(u,v)∈C0(¯Ω×[0,∞))∩C2,1(¯Ω×(0,∞))是方程组(5)的经典解,且初值u0、v0满足(6)式,则存在m,A,L >0,使得对任意的t >0,只要
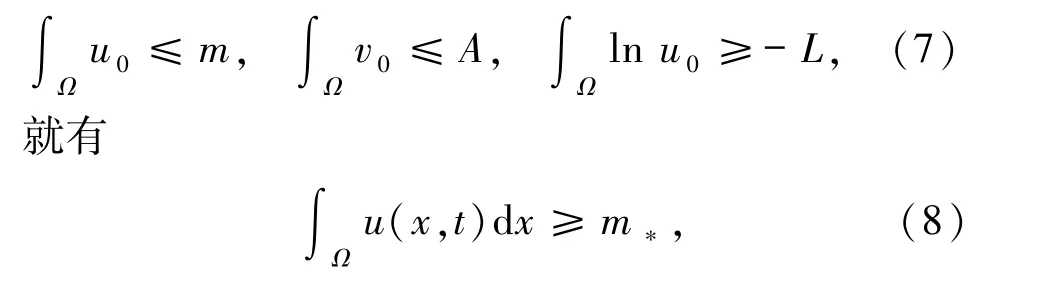
其中m*=m*(m,A,L,χ,r,μ,Ω)>0.
2 一些基本的估计
引理2.1设(u,v)是方程组(5)的非负全局经典解,χ,r >0 且μ >μ0,初值u0、v0满足(6)式.则对任意的t >0 有
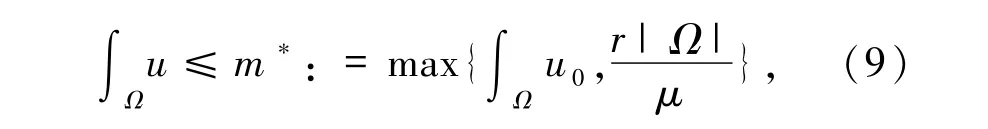
且对任意的t0≥0 和T >0 有

证明将方程组(5)的第一个方程关于变量x在区域Ω内积分有
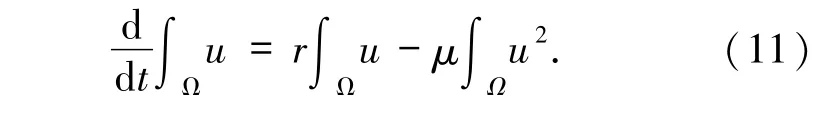
由Cauchy-Schwarz不等式知:
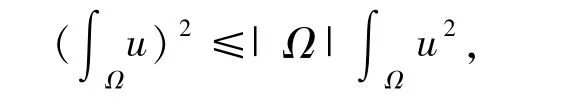
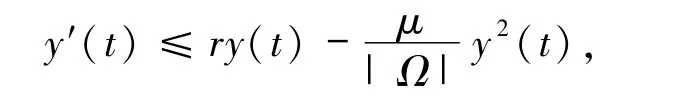
再由常微分方程的比较原理可以得(9)式.将(11)式关于时间t∈(t0,t0+T)积分,再由u 的非负性可得

即(10)式成立.
以下两个引理是研究信号消耗趋化模型时常用到的基本引理(可参看文献[15-17]).
引理2.2设(u,v)是方程组(5)的非负全局经典解,初值u0、v0满足(6)式.则对任意的t >0 有
‖v(·,t)‖L∞(Ω)≤‖v0(·,t)‖L∞(Ω)=:C∞.(12)
证明将方程组(5)的第2 个方程两边同时乘以vp-1,再关于空间变量x 在区域Ω 内积分,利用分部积分公式及u、v 的非负性可知,对任意的t >0 有

引理2.3设(u,v)是方程组(5)的非负全局经典解,初值u0、v0满足(6)式,则有

其中C∞是由(12)式所定义的常数.
证明将方程组(5)的第2 个方程两边同时乘以v,再关于空间变量x在区域Ω内积分,则对任意的t >0 有
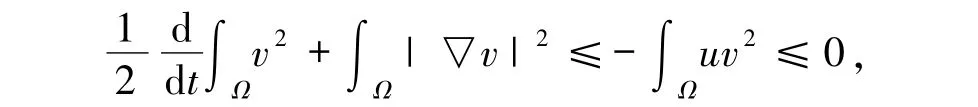
再对时间积分有

其中C∞是由(12)式所定义的常数.当t→∞时,可证得(13)式.
本节是为证明主要结论做一些准备.特别地,将对函数∫Ωln u进行分析并推导出它的一个下界.
引理3.1设(u,v)是方程组(5)的非负全局经典解,χ,r >0 和μ >μ0,且u 在区域¯Ω ×(0,∞)内非负,则对任意的t >0 有
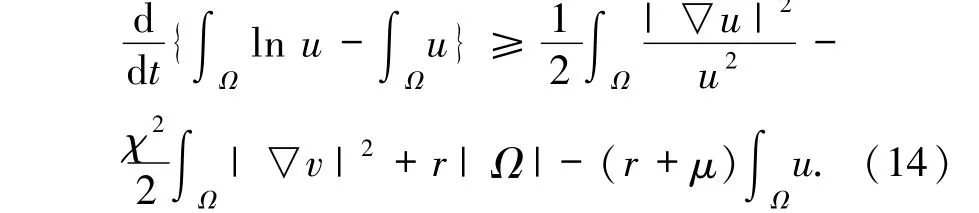
证明将方程组(5)的第一个方程两边同时乘以,再利用Young不等式有

结合(15)和(11)式可得(14)式.
引理3.2设(u,v)是方程组(5)的非负全局经典解,χ,r >0 且μ >μ0,若存在t0,L0≥0 和T >0,满足

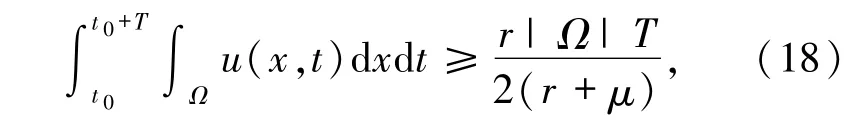
其中m*和C∞分别是引理2.1 和(12)式所定义的常数.
证明由(14)式可知,对任意的t >t0有

再令t:=t0+T,则由(16)式、引理2.3 和u 的非负性可知

又因为对任意的ξ >0,有ln ξ≤ξ,即可得
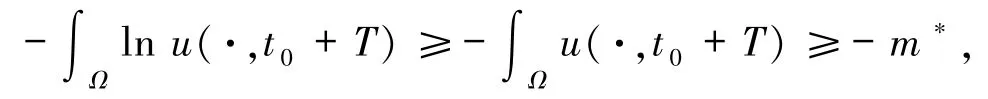
再由(17)和(19)式可知

即(18)式得证.
由引理3.2 的结论,可以直接得到下面的估计.
引理3.3设(u,v)是方程组(5)的非负全局经典解,χ,r >0 和μ >μ0,且t0,L0≥0 和T >0 分别满足(16)和(17)式.则
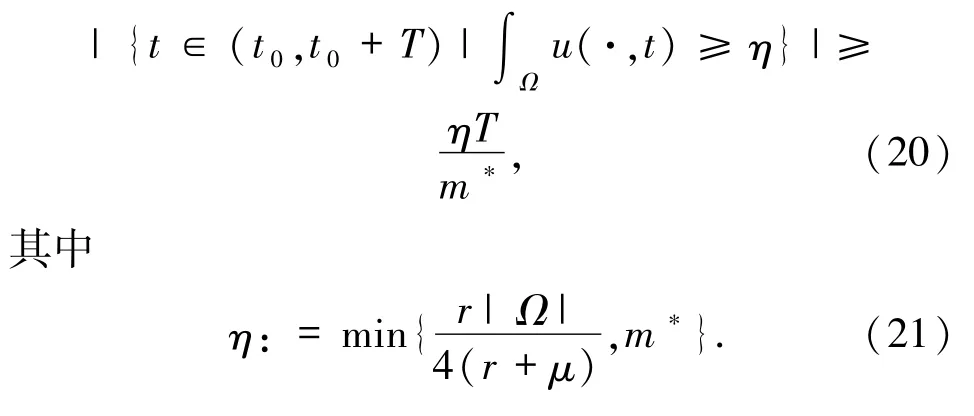
证明令

因此,由引理3.2 可知
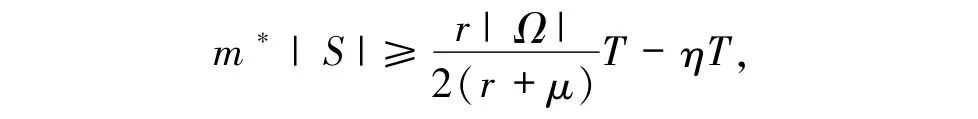
再由η的定义可证得(20)式.
引理3.4设(u,v)是方程组(5)的非负全局经典解,χ,r >0 且μ >μ0,令T,K >0,t0≥0,则有

其中m*是由(9)式所定义的常数.
证明令

因此,由(10)式可以直接得到(22)式.
引理3.5设(u,v)是方程组(5)的非负全局经典解,χ,r >0 和μ >μ0,且t0≥0 和L0>0 满足(16)式,则对任意的M,T >0 有

其中m*和C∞分别是由(9)和(12)式所定义的常数.
证明将(14)式关于时间t∈(t0,t0+T)积分,则由引理2.1、引理2.3 和(16)式以及

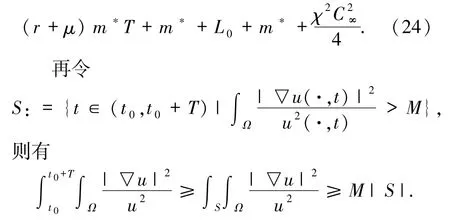
再结合(24)式可证得(23)式.
引理3.6令η,K >0,则对非负函数ψ ∈L2(Ω),若满足

证明引理的证明可参看文献[14]的引理4.1.
引理3.7假设φ∈C1()是一个正的函数,且对任意的ε,σ >0,若满足

则存在一个常数C(ε)>0,使得

证明引理的证明可参看文献[14]的引理4.3.
引理3.8令m,A,L >0,设(u,v)是方程组(5)的非负全局经典解,χ,r >0 和μ >μ0,且u0∈C0(¯Ω),v0∈C0(¯Ω)满足
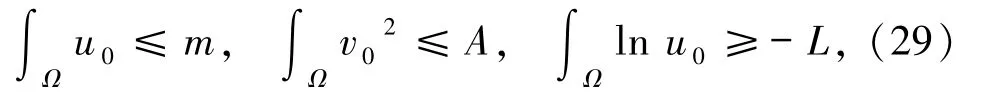
则可以找到一数列(tk)k∈N⊂[0,∞),使得有
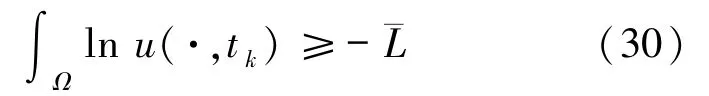
成立,其中¯L =¯L(m,L,r,χ,μ,Ω)和T =T(m,A,L,r,χ,μ,Ω)都为正常数,k∈N,tk<tk+1<tk+T,且当k→∞时,有tk→∞.
证明令
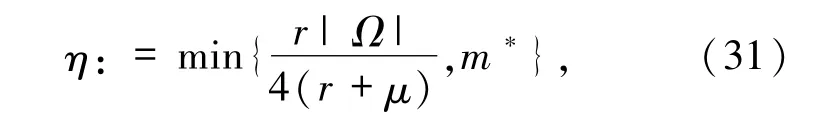
取适当的K,M >0 满足
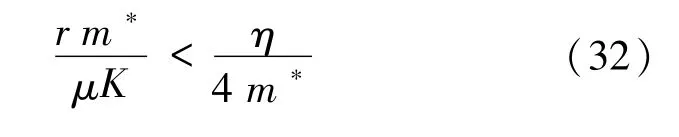
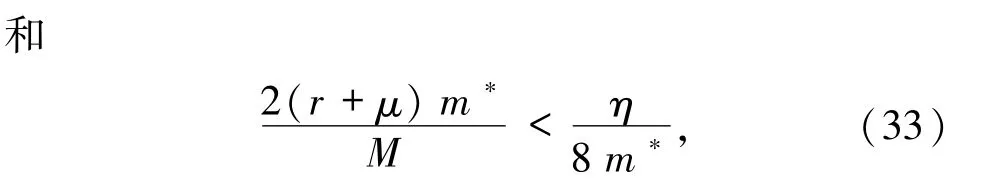
其中m*>0 是由引理2.1 所定义的常数.记

对引理3.8 的证明主要是利用微分不等式(14)和一个迭代理论.令
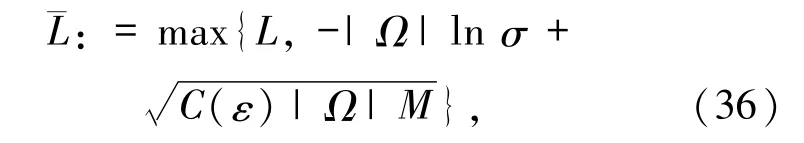
其中C(ε)是由引理3.7 所给定的常数.固定适当大的T >0 满足

其中C∞是由(12)式所定义的常数.
在上面的假设条件下,需要证明(30)式成立.以下运用数学归纳法对其进行证明.令t1=0,并且假设当j∈{1,2,…,k}时,有

成立.接下来证明当j =k+1 时,存在

使得(40)式同样成立.
为此,引入集合

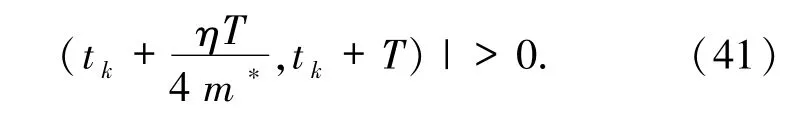
取L0:=,t0:=tk,则当j =k 时,由(39)和(40)式可得(16)和(17)式.再由引理3.3 和η 的定义可得

其次,由(31)式可知η≤m*,即有

取t0:=tk,再根据(32)和(38)式以及引理3.4可得
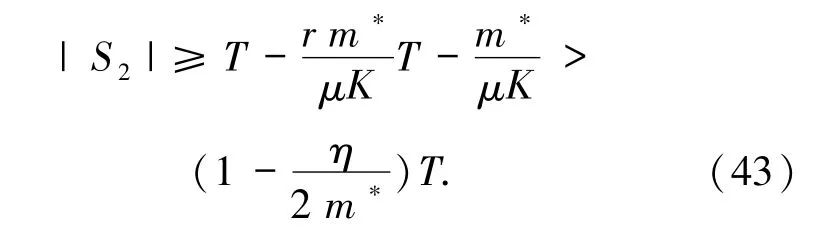
最后,由(40)式和引理3.5 可知

再根据(33)和(37)式可知
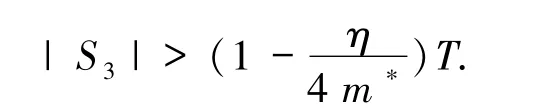
结合(42)和(43)式可得

即(41)式得证.
接下来证明对任意的t∈S1∩S2∩S3有
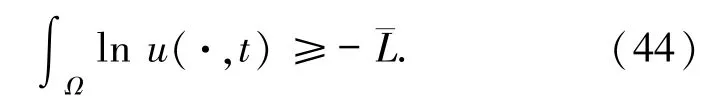
为此,固定t∈S1∩S2∩S3,再根据引理3.6 以及σ和ε的定义,可得

因此,由引理3.7 可知
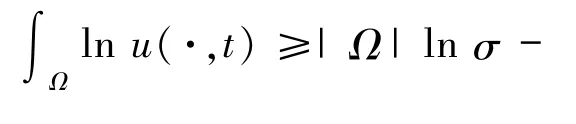

由于t也属于S3,故有

再由(36)式可得(44)式.因此,当j =k+1 时,存在

使得(40)式成立,即引理得证.
4 主要结果的证明
结合引理3.8 和引理3.3 可以得证本文的主要结论.
定理1.1 的证明由引理3.8 知,存在数列(tk)k∈N⊂[0,∞),使得当k→∞时,有tk→∞,且对所有的k∈N,有

成立.令t0:=tk,再根据引理3.3 知,存在~tk∈(tk,tk+T),使得
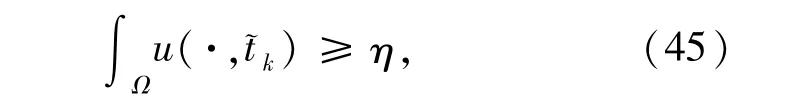
其中η是由(21)式所定义的常数,且对任意的k∈N,有.
又因为对任意的t >0,有
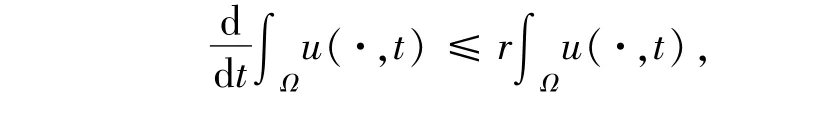
再结合(45)式,对任意的t∈[0,~tk)有

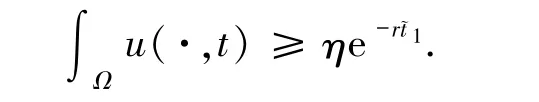
对于较大的时间t,当k≥2 时,由tk<tk-1+T和tk<<tk+T 可以推出<+2T.因此,由(46)式可知,对任意的有
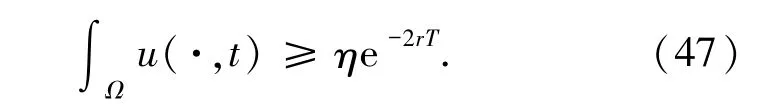
取m*:=min{ηe-2rT,ηe-r~t1},又因为当k→∞时,有~tk>tk→∞,再结合(47)式可得证(8)式.

