循环荷载下水泥土桩复合体动力参数试验研究

叶观宝 ，秦粮凯 ，张 振 ，郑文强,3 ，陈 勇

（1.同济大学土木工程学院地下建筑与工程系，上海 200092；2.同济大学岩土及地下工程教育部重点实验室，上海 200092；3.上海勘察设计研究院（集团）有限公司，上海 200093）

水泥搅拌桩被广泛应用于软土地基处理中[1]，处理后的软土路基要承受长期往复交通荷载，因此水泥土桩复合体的动力特性也备受关注。

叶观宝等[2]结合现场试验得出水泥土桩承载力、基底反力、荷载传递等规律。刘松玉等[3]结合某高速公路工程进行钉形水泥土桩的现场研究。叶观宝等[4]从土体、水泥土及复合桩体单元变形模式出发对加芯水泥土桩复合地基桩土应力比建立理论计算公式。白顺果等[5]采用室内模型试验得出水泥土复合地基随着循环应力比增大，沉降速率也越大。Kim等[6]以离心机动力试验模拟结构物、浅基础与结构物下水泥土加固地基在神户地震波下动力响应进行研究，随着振动加速度的增大，置换率24%的模型比置换率33%先达到破坏。Liu等[7]对水泥土桩复合体进行单剪与循环剪切试验。Cai等[8]、曾国红等[9]、吕程伟[10]及Kazemian等[11]分析了水泥土复合单元体静动力特性。然而，目前的研究大多集中在水泥土桩复合地基的静力特性[12-13]和水泥土的动力特性[7]，对循环荷载作用下水泥土桩复合体动力特性的研究较少。

本文利用GCTS-STX600大型三轴仪，开展水泥土桩复合体大型动三轴试验，研究围压、静偏应力、置换率及分级加卸载路径对其动力参数的影响，并分析了动力参数的波动性。

1 试验方案与试样制备

1.1 试验设备及方案

试验设备包含GDS动三轴仪和GCTS大型静动三轴仪。动三轴仪进行软土以及水泥土循环动力试验。大型静动三轴仪主要进行水泥土桩复合体静动力试验，如图1所示。GCTS大型动静三轴试验机可同时独立施加、改变和控制试样的轴向荷载、围压和反压及加载速率，进行静态、动态三轴试验。试验机可产生轴向加载频率为0～10 Hz的正弦波、方波、三角波和用户自定义波形，轴向力加载精度±0.01 kN，围压精度±0.1 kPa。

图1 GCTS大型三轴仪Fig.1 GCTS large scale triaxial apparatus

试验方案主要考虑围压、动应力分级加卸载路径、静偏应力以及置换率对水泥土桩复合体动力特性的影响。加载形式分为分级加载和分级卸载：分级加载的动应力共分5级，每级循环2 500次，依次动应力比为0.25，0.30，0.35，0.40，0.45；分级卸载动应力比次序与之相反。软土的动强度较小，软土动三轴试验选用动应力比为0.15。相关研究[14-17]表明，交通荷载在路基内部产生的动应力频率一般在0.1～5 Hz，且以1 Hz左右低频分量为主，且可采用半正弦波来描述交通荷载作用下地基土中动应力。因此，本试验采用1 Hz的半正弦波来模拟交通荷载作用下地基土中的动应力。加（卸）载示意图如图2所示。围压采用40，60，80 kPa。试验方案见表1。

表1 试验方案Table 1 Test scheme

图2 分级循环加（卸）载示意图Fig.2 Schematic diagram of staged cyclic loading (unloading)

1.2 试验材料

试验材料包括土、水泥和水。试验用粉质黏土，密度为1.66 g/cm3，含水率为25.0%，液限为36.3%，塑限为21.2%。采用普通硅酸盐水泥（P.O 32.5）、自来水。水泥土模型桩的直径分别选取100，120，140 mm。水泥土模型桩水泥掺量10%，水灰比取1。将制备的水泥土浆液置于模型桩模具内振捣，静置48 h后拆模，并置于标准养护室浸水养护龄期60 d，测得水泥土峰值强度为0.93 MPa。水泥土强度在实际工程典型范围内[1-2]。

图3为水泥土桩复合单元体大型三轴试验试样示意图。大三轴试验试样的直径300 mm，高度600 mm。试样制作时，在大型三轴模具底层放置一层滤纸，在模具中央放置水泥土模型桩；按含水量控制加入一定量水并充分搅拌软土；按软土天然密度分批次称量充分搅拌后的软土，逐层填入模具内，并压实至制定高度；重复操作至模具内填满软土；将试样顶面刮至齐平，铺上一层滤纸，再将加载顶盖轻轻放置在试样顶部。制作完成的试样如图4所示。将试样置于仪器中，在相应围压下进行固结，待体积变化稳定后（本文试验采用静置12 h）进行GCTS动三轴试验。

图3 水泥土桩复合单元体示意图Fig.3 Schematic diagram of unit cell of composite soil with DM column

图4 GCTS大型三轴试样制作Fig.4 Specimen preparation of the GCTS large-scale triaxial test

软土动三轴试验试样采用天然含水率的重塑土，分层填入饱和器中，用击实器将土样击实，重复操作至饱和器顶部，将试样顶面刮至齐平，静置12 h备用。水泥土动三轴试验试样采用与大型动三轴试验中水一致的水泥土浆液，分批次灌入饱和器内，沿侧壁捣实，再将饱和器置于小型振动台上，振动60 s后，重复操作至饱和器顶部，并用刮刀刮平，套上保鲜膜静置养护24 h后，拆模置于标准养护室浸水养护60 d备用。

2 软土与水泥土动力参数

2.1 软土的动力参数

图5为软土试样在不同静偏应力下动力参数随循环振动次数关系曲线。由图5（a）可知，在不同静偏应力下，动弹模量随振次增加而减小；随静偏应力增加，动弹模量逐渐减小。静偏应力40 kPa下，软土试样加载初期应变迅速增加至20%，试样出现明显鼓胀破坏。由图5（b）可知，在不同静偏应力下，阻尼比在振动荷载初期增加较快，而后逐渐趋于稳定。在试验静偏应力和动应力比范围内，软土试样动弹模量稳定值为15～70 MPa，阻尼比稳定值为0.05～0.10。试样在40 kPa静偏应力下虽然出现鼓胀破坏，但由于试验为应力控制，随着应变增加，试样与动荷载达到平衡状态，动弹模量也出现显著衰减。

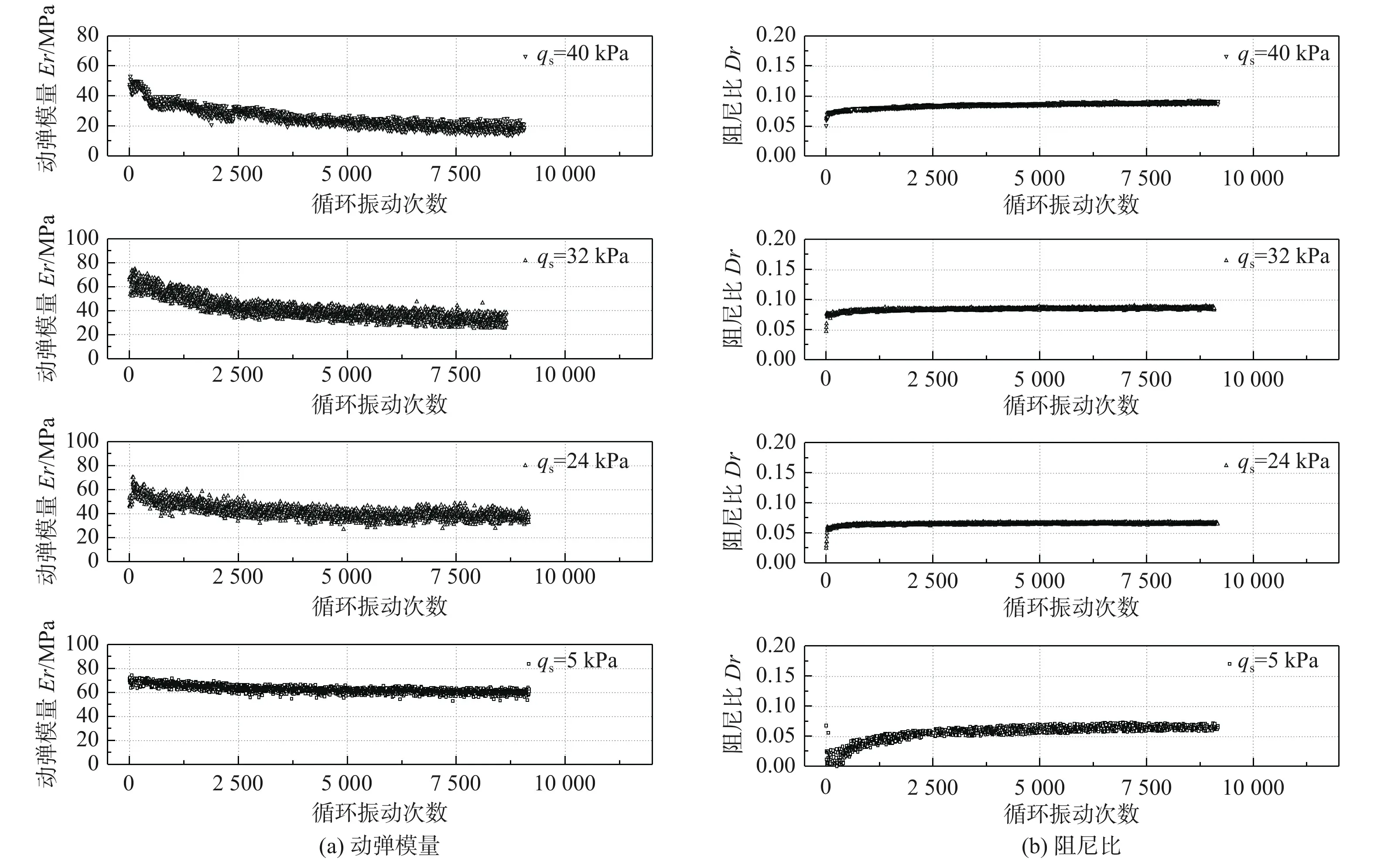
图5 不同静偏应力下软土动力参数与循环振次的关系Fig.5 Dynamic parameter vs cyclic loading times under different static deviator stresses of the soft clay

2.2 水泥土的动力参数

图6为水泥土在不同静偏应力下动力参数随循环振动次数关系曲线。由图6（a）可知，在不同静偏应力下，动弹模量随振次增加略有增加；随静偏应力增加，动弹模量逐渐增大，这可能是由于静偏应力作用一定程度地使得试样结构性更强。由图6（b）可知，在不同静偏应力下，阻尼比在振动荷载初期迅速衰减，而后逐渐趋于稳定。静偏应力为5 kPa时，阻尼比随动应力增加而减小；而静偏应力为24～40 kPa时，阻尼比随动应力幅值增加而增加。在试验静偏应力和动应力比范围内，水泥土动弹模量稳定值为100～125 MPa，阻尼比稳定值为0.03～0.075。

图6 不同静偏应力下水泥土动力参数与循环振次的关系Fig.6 Dynamic parameter vs cyclic loading times under different static deviator stresses of the composite soil with deep mixed column

3 水泥土桩复合体动力参数

3.1 围压的影响

图7为置换率为11.1%时不同围压下水泥土桩复合体动力参数随循环振动次数的关系曲线。由图7（a）可知，在逐级加载情况下，围压对动弹模量影响差异并不明显。随着动应力比增加，动弹模量略有下降，但在相同动应力振级范围内，动弹模量随振次变化不大，这可能是因为动应力水平相比其强度较低。图7（b）为不同围压下阻尼比随振次的变化曲线。随着围压越大，同一振次下的阻尼比越小；随着动应力幅值的增加，阻尼比略有减小。在试验围压和动应力比范围内，动弹模量稳定值为100～130 MPa，阻尼比稳定值为0.05～0.15。

图7 不同围压下动力参数与循环振次的关系Fig.7 Dynamic parameter vs cyclic loading times under different confining pressures

3.2 静偏应力的影响

图8为置换率为11.1%时不同静偏应力下水泥土桩复合单元体动力参数随振次的变化曲线。随着静偏应力的增加，试样动弹模量逐渐减小，而阻尼比显著增大。静偏应力为32 kPa和40 kPa、动应力比分别为CSR=0.40与CSR=0.35时，试样出现应变陡增（试样破坏），试样动弹模量迅速衰减，阻尼比迅速增加。可知，随着静偏应力的增加，水泥土桩复合单元体的临界动应力比减小。

图8 不同静偏应力下动力参数与循环振次的关系Fig.8 Dynamic parameter vs cyclic loading times under different static deviator stresses

3.3 置换率的影响

图9为围压80 kPa和静偏应力5 kPa时不同置换率下水泥土桩复合单元体动弹模量与阻尼比随振动次数的变化曲线。随着置换率从11.1%增加至21.7%，试样的动弹模量略有增加，阻尼比略有减小。Chai等[8]研究结果也表明，置换率在5%～20%范围，小应变（10-4）情况下提高置换率可提高水泥土桩复合体动弹模量，但随着应变的增加，两者的动弹模量逐渐趋于一致。这可能是因为水泥土桩复合单元体的动力特性受到水泥土和桩间软土的共同影响。试验中，虽然增加了水泥土桩置换率，但软土的占比仍较大。

图9 不同置换率下动力参数与循环振次的关系Fig.9 Dynamic parameter vs cyclic loading times under different area replacement ratios

3.4 动应力分级加卸载的影响

图10为置换率为11.1%时分级加卸载情况下动弹模量与阻尼比随振次变化曲线。加卸载情况下，动弹模量稳定值为100～120 MPa，阻尼比稳定值为0.05～0.075。但相同振次下，相比于分级加载，分级卸载的动弹模量略小，阻尼比略大。这可能是因为分级卸载第一级动应力幅值较大，试样内部在振动过程早期出现了裂缝，并随振动次数增加不断发展，造成复合单元体的动力参数劣化。

图10 动应力分级加卸载下动力参数与循环振次的关系Fig.10 Dynamic parameter vs cyclic loading times under different static deviator stresses under staged loading/unloading

4 动力参数讨论与分析

4.1 动力参数波动性分析

由试验结果可知，在循环荷载下，土、水泥土和水泥土桩复合单元体的动力参数集中在一定范围内波动。为研究试样动力参数的波动性，选取每级动应力下最后500次，即应变稳定后的动力参数进行分析。通过正态分布验证（图11）表明，动力参数服从正态分布。据此计算出各组试验动力参数的均值、标准差和变异系数，并分析土、水泥土和水泥土桩复合单元体的动力参数波动程度。

图11 正态分布检验Fig.11 Verification of normal distribution

图12为不同静偏应力下软土、水泥土和水泥土桩复合单元体动力参数变异系数计算结果。软土、水泥土和水泥土桩复合单元体，三者动弹模量变异系数分别为0.61%～5.36%、0.40%～0.82%和1.08%～1.73%，三者阻尼比的变异系数分别为4.21%～12.37%、2.21%～4.87%和3.55%～7.97%。三者动弹模量的变异性均小于阻尼比，即阻尼比波动性更明显。水泥土和水泥土桩复合单元体的动力参数变异性要小于软土，即软土的动力参数波动性更明显。本试验置换率和静偏应力范围内，其对软土、水泥土和水泥土桩复合单元体的动力参数变异系数的影响规律不明确。

图12 不同静偏应力下不同材料的动力参数变异系数Fig.12 Coefficient of variation of dynamic parameter of different materials under different static deviator stresses

4.2 动力参数对比

表2归纳了试验中软土、水泥土和水泥土桩复合单元体动力参数的上下限范围，造成试样破坏的动应力比阶段除外。从表2中可知，三者的动弹模量差异较大，阻尼比差异较小。图13为三者动力参数对比直方图。随着静偏应力增加，软土的动弹模量逐渐减小，呈软化状态；水泥土的动弹模量逐渐增加，呈硬化状态；复合体的动弹模量略有减小。对于复合体，动弹模量随着置换率增加而增加。相比于软土，复合体动弹模量提高了2～6倍，静偏应力越大，提高系数越大。

图13 不同静偏应力下不同材料的动弹性模量Fig.13 Dynamic elastic modulus of different materials under different static deviator stresses

表2 不同材料的动力参数取值范围Table 2 Value ranges of dynamic elastic modulus of different materials

5 结论

（1）随着静偏应力增加，复合单元体动弹模量减小，阻尼比增大，临界动应力比减小。随着置换率增加，动弹模量略有增加，阻尼比略有减小。逐级卸载会造成复合单元体的动力参数劣化。

（2）软土、水泥土和水泥土桩复合单元体的动力参数的波动性均符合正态分布。三者动弹模量的变异性均小于阻尼比，复合单元体阻尼比的变异系数是动弹模量的2.8～7.0 倍。水泥土和水泥土桩复合单元体的动力参数变异性要小于软土。

（3）随着静偏应力增加，软土呈软化状态，水泥土呈硬化状态，复合体呈轻微软化状态。相比于软土，复合体动弹模量提高了2～6 倍，静偏应力越大，提高系数越大。