高阶线性Gronwall不等式的推广及应用

廖玲蓝,王朋杰,张 洁

(贵州师范大学 数学科学学院，贵州 贵阳 550025)

数学物理方程的能量估计[1]和解的存在唯一性[2]是微分方程最重要的内容之一，而微分与积分形式的Gronwall不等式[3-4]求解思想是得到能量估计和解的存在唯一性的关键，该方法是通过指数函数求导来求解方程的。由于方程因时间和空间变化的多样性，一阶线性Gronwall不等式不能满足现阶段方程的需求，因此相关的高阶线性Gronwall不等式[5-9]求解方法的研究受到了学者的极大关注。文献[3]研究了含有2个函数的一阶线性Gronwall不等式；文献[4]研究了二阶线性常数项Gronwall不等式；文献[5]研究了含有一阶、二阶、常数项的Gronwall不等式。本文在文献[3-5]的基础上进行推广，构造三阶或者含有2个函数的方程，通过一阶线性Gronwall不等式求解方法实现对高阶线性Gronwall不等式的求解，最后将得到的解结合实例来具体分析。

1 Gronwall不等式的主要性质

引理1[1](Gronwall不等式)令η(·)是[0,T]上的非负绝对连续函数，满足几乎处处于t的导数不等式η′(t)≤φ(t)η(t)+ψ(t)，其中ψ(t)是φ(t)非负可积函数，则

0≤t≤T。

2 高阶Gronwall不等式的推广与证明

Gronwall 不等式的广泛应用解决了大量微分方程问题。例如一阶Gronwall不等式用于解决常微分中解的唯一性问题；二阶Gronwall不等式能更好解决方程的能量估计问题等；而对于三阶Gronwall不等式只含一个函数时，目前的研究还不是很完善。下面本文接着讨论三阶线性并含有2个函数的Gronwall不等式，从而得到了类似于二阶Gronwall不等式的结果。

(1)

则存在常数m1,m2使得

+k4)dξ，

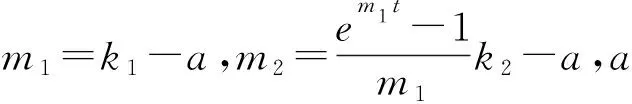
证明文献[5]研究g(t)=u(t)的情况，并且得到了结果u(t)≤c,c为正常数。下证g(t)≠u(t)的情况。

由于k1>0，则存在正常数a>0，使得m1=k1-a>0，在式(1)的两端乘e-at，则

k3e-atg(t)+k4e-at;

(2)

在式(2)的两端减ae-atu″(t)，则

(3)

令F(t)=e-atu″(t),G1(t)=k2e-atu′(t)+

k3e-atg(t)+k4e-at，由u″(0)=0得到F1(0)=0,从而式(3)可整理为

(4)

在式(4)的两端减ae-atu′(t)，则

(5)

由u′(0)=0得F2(0)=0,从而式(5)可整理为

代入F2(t),G2(t)以及引理2得

整理并且对t∈[0,T]积分，代入u(0)=0得

+k4)dξ,

一般高阶Gronwall不等式的“高”只会体现在u(t)上，对于含有2个函数的不等式，文献[5]已经讨论了g(t)为常数或者是一阶线性函数的情况，下面讨论g(t)为二阶线性函数的情况，得到类似g(t)为一阶线性函数的结果。

定理2设u(t),g(t)满足

(6)

且g(t)≥0,c2<0,c1为正常数，u″(0)=u′(0)=

u(0)=0，g′(0)=g(0)=0,则存在正常数c，使得

u(t)≤0。

证明整理(6)得

(7)

在式(7)的两端乘e-c2t，则

(e-c2tu″(t)+e-c2tg′(t))′≤c1e-c2t

+((c2e-c2tu(t))′+c2e-c2tu′(t)+c2e-c2tg(t))′；

(8)

式(8)两端在t∈[0,T]上积分，并且带入边值条件有

(9)

式(9)两端在t∈[0,T]上积分，代入边值条件并且消去e-c2t，有

由c1>0,c2<,g(t)≥0得

由引理1得u(t)≤c。

对于二阶连续可微函数，当g(t)=c=常数时，文献[4]已经得到通解，下面将讨论如何在g(t)≠c的情况，得到类似文献[4]的结果。

定理3设u(t)是定义在[0,T]上的二阶连续可微函数,g(t)在[0,+∞]上可积，存在正常数c，使得

(10)

证明在式(10)的两端乘ec1t，则

u″(t)ec1t≤cu(t)ec1t+g(t)ec1t,

上式对t∈[0,T]积分，由分部积分公式得

u′(t)ec1t-u(0)≤c1u(t)ec1t-c1u(0)

(11)

在式(11)的两端乘e-2c1t，则

u′(t)e-c1t-u′(0)e-2c1t≤c1u(t)e-c1t

上式对t∈[0,T]积分并且使用分部积分公式得

整理化解后得

3 应用举例

最后本文将讨论以上定理在双曲型能量估计不等式中的应用。

(12)

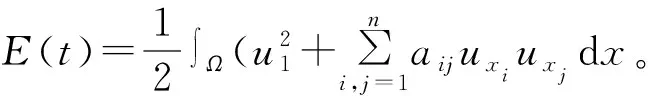
利用格林公式进行分部积分，并且代入初边值条件得

(13)

(14)

(15)

其中c1为一个与u无关的函数，由弗里德里克斯不等式[2]得

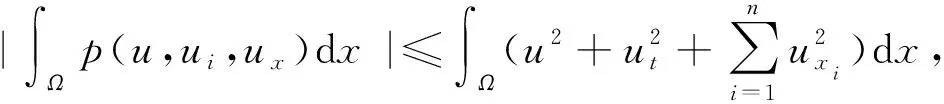
(16)

由Young不等式[1]得

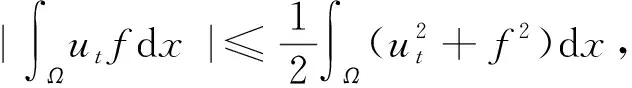
(17)

将(14)～(17)代入(13)有

其中c是与u无关的正常数，由引理1得

4 结语

本文主要是对u(t)、g(t)进行推广改进，将一阶、二阶线性形式函数u(t)推广到三阶线性形式，将常数形、一阶线性形式函数g(t)推广到二阶线性形式，从而得到与文献[3]～[5]类似的估计。根据本文推广的形式，后续可以继续改进推广到更高阶线性形式。