非Hermite线性方程组的迭代终止条件

廖晓花

(闽南理工学院 信息管理学院，福建 石狮 362700)

微分方程和积分方程已经广泛应用于量子化学、流体力学、声散射等工程应用和科学计算领域中[1]。有限差分以及有限元等离散化技术中的微分方程和积分方程复线性方程组求解主要包括以下两类：复线性方程组，Ax=b；存在多右端项的复线性方程组，AX=B。其中A∈Cn×n表示非Hermite矩阵，x，b∈Cn，X,B∈Cn×p,p=n。

求解大规模线性方程组在实际工程问题数值计算中所占比重高[2]；非线性方程组的高效求解是众多研究学者的研究方向，其高效的求解具有较高的应用价值以及理论意义[3]。目前普遍通过Krylov子空间方法研究存在多右端项以及普通非Hermite线性方程组的求解。

非Hermite线性方程组实际应用中对计算规模、计算效率以及存储量等要求较高[4]，采用Krylov子空间方法往往无法满足这些需求，为此，非Hermite线性方程组的迭代终止条件研究具有较大的必要性。

非Hermite线性方程组求解的预处理方法可有效提升求解效率[5]。探究非Hermite线性方程组的迭代终止条件，采用预处理方法完成对CORS算法的处理后，再利用处理后的CORS算法求解非Hermite线性方程组，使其快速迭代，可提升非Hermite线性方程组的收敛速度、鲁棒性以及稳定性。

1 非Hermite线性方程组的迭代终止条件

1.1 非Hermite线性方程组预处理

通过预处理方法预先处理非Hermite线性方程组可提升其求解速度[6]，然后再将预处理完成的非Hermite线性方程组利用迭代算法快速求解。

本文采用预处理方法与实线性方程组加速求解的方法建立预处理条件子M-1，令所建立与处理条件子与系数矩阵A的逆矩阵近似，即M-1≈A-1，且M-1≈(M1M2)-1。获取的非Hermite线性方程组的CORS方法预处理公式为

(1)

预处理具有多个右端项的非Hermite线性方程组时，可使M1=I，M2=M，利用以上仅考虑右端项的预处理方法，系数矩阵内奇异值分布较为聚集[7]，从而提升迭代算法的收敛速度。

1.1.1 选取预处理条件子

设

A=(aij)n×n=D-N。

(2)

式中D=diag(d1,d2,…,dn)，且需满足

那么

A-1=(D-N)-1=(I-D-1N)D-1。

(3)

式中I表示单位矩阵。

已知存在公式：

(I-D-1N)-1≈I+D-1N+…+(D-1N)q-1，

(4)

可得预处理条件子M-1公式：

M-1=(I+D-1N+…+(D-1N)q-1)D-1。

(5)

式中q≥1。

通过确定预处理条件子M-1可知，非Hermite线性方程组计算量随着内迭代次数的提升而有所增加[8-9]，非Hermite线性方程组预处理的内迭代次数对于提升最终计算的收敛速度极为重要。

1.1.2 预处理CORS算法

预处理CORS算法过程如下：

3)当‖rk‖2≤ε‖r0‖2时，终止求解，此时ε∈R+；否则需求解

4)令k=k+1，返回至步骤2)。

forl=0,1,…,q-1

end

(6)

forl=0,1,…,q-1

end

(7)

迭代次数范围固定时，内迭代次数q的增多令系数矩阵特征值聚集程度有所提升[10-11]，令非Hermite线性方程组求解速度有所提升。

1.2 非Hermite线性方程组的迭代终止条件

基于CORS方法求解非Hermite线性方程组，令非Hermite线性方程组快速满足迭代终止条件[12]。

广义CORS方法参量符合公式：

(8)

(9)

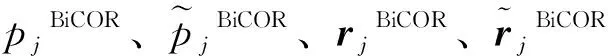
j+1过程。

j+1。

已知公式如下：

(10)

获取递推过程如下：

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

将公式(17)与公式(18)结合可得公式：

(19)

获取辅助迭代向量公式为

(20)

可得迭代序列公式如下：

sj=tj-αjApj，

(21)

(22)

(23)

(24)

uj+1=rj+1+βj+1hj，

(25)

(26)

(27)

(28)

以及

(29)

从而得到

(30)

以及

(31)

(32)

以及

(33)

通过以上推导过程得到高效迭代终止的非Hermite线性方程组的广义CORS方法过程如下：

(1)用x0表示初始值，求解r0=b-Ax0；

(4)求解j=0,1,2,…；

(6)αj=ρj/σj；

(8)sj=tj-αjqj；

(20)uj+1=rj+1+βj+1hj；

计算结束。

该方法的误差界公式为

(34)

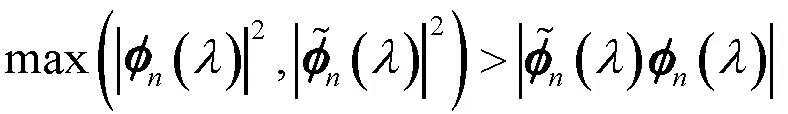
2 算例分析

在MATLAB环境下运行算例的全部计算过程。

已知2个非Hermite线性方程组：

方程组A：A1x=b1;

方程组B：A2x=b2;

采用随机算法求解以上2个非Hermite线性方程组，结果如表1所示。

表1 线性方程组求解结果

由表1可知，采用随机算法通过常用的终止迭代条件求解非Hermite线性方程组将提前终止求解，使获取的迭代解与精确解相差较大。

将本文方法与TFQMR方法和GCORS2方法对比，统计不同方法求解以上公式的迭代过程计算量，统计结果如表2所示。

表2 不同方法计算量

表2中，AXPY表示执行向量x、y以及纯量α的运算α×y+x。由表2中统计结果可知，本文方法相比于TFQMR方法和GCORS2方法所执行AXPY运算较少。

设置停机准则TOL为10-5及10-8，得到的数值结果如表3所示。

表3 不同方法数值结果

由表3可以看出，利用本文方法求解线性方程组的收敛速度明显高于另2种方法。不同停机准则情况下，本文方法所需的迭代步数以及CPU执行时间明显低于另2种方法，且可得到最精确的近似解。以上算例计算结果表明，利用本文方法，迭代过程中的残量范数较高，具有较快的收敛速度，可在较少迭代次数情况下快速获取最优解，迭代次数低、稳定性高。

3 结论

由于非Hermite线性方程组存在于应用数学、物理学以及控制论等各类学科中，所以，非Hermite线性方程组的求解问题是应用数学中的一个十分重要的分支。但是，由于目前非线性方程组的理论研究还有欠缺，所以其应用价值还不能充分发挥。本文的主要研究亮点如下：

1)对CORS方法进行预处理，可提升利用广义CORS方法求解非Hermite线性方程组的效率、收敛速度，实现求解结果的实时性；

2)利用残量多项式建立的广义CORS求解非线性方程，由于存在不规则收敛残量范数，易造成非线性方程解误差较高、近似解较差的问题，而经过本文方法求解后可避免初始误差加大，进一步提升了收敛速度与光滑性；

3) 经过预处理算法处理的广义CORS方法求解非Hermite线性方程组时，收敛速度提升至最高，可通过最小的迭代时间和迭代次数实现快速终止，因此，本文方法在求解结果精确度与计算量均具有一定的优势性。