一种改进的KFF-AGC方案

杨 扬，张 飞，肖思竹

（1.中国恩菲工程技术有限公司，北京 100038；2.北京科技大学 高效轧制及智能制造国家工程研究中心，北京 102206）

0 引言

随着当前市场对成品带钢质量要求的逐渐提高，轧机控制性能的提升也面临着极大的挑战。热轧带钢的出口厚度精度是产品质量的重要指标，厚度设定模型和自动厚度控 制（Automatic Gauge Control，AGC）系 统 一 直 是热轧带钢自动化实现的重要功能。AGC系统的功能是在轧制过程中，在面对轧件与设备产生扰动时，出口带钢厚度依旧保持厚度恒定或最小的变化。长期以来，AGC系统以压力AGC（GM-AGC或称RF-AGC）和监控AGC（MN-AGC）为主体。传统AGC是以厚度偏差为依据来控制厚度，这对于来料厚差的消除是有效的，但对于来料硬度在每一机架重发性产生的厚差，只能在“事发后”对设有反馈AGC的这架轧机加以纠正，因而不能有效消除厚差。20世纪90年代以来，出现了研究新的前馈AGC的潮流。其中，以加拿大Hatch Steltech推出的FFF-AGC最为著名，近年韩国POSCO亦推出了新的FF-AGC[1]。国内对前馈AGC的研究和应用也进入了一个新的阶段，文献[2]根据影响系数分析法认为，造成热带厚差的主要原因是带钢全长的温度不匀产生的“硬度”波动，并在某钢厂1700mm热连轧上使用了将硬度信息前馈的自动厚度控制（Kfeed-forward Automatic Gauge Control，KFF-AGC） 方 案， 取 得了良好的控制效果。

经过在现场的长期观察和大量数据的分析，发现KFFAGC策略存在一定缺陷，对某些规格的钢种不能有效消除水印厚差和头尾厚跃。图1所示的曲线是来自某钢厂1700mm热连轧现场采集到的数据，从图中可以看出，轧制生产线采用了KFF-AGC方法后，带钢头部鼓包、水印部分和尾部尖峰超差均达100µm以上，前馈AGC的优点并没有得到充分发挥。这与KFF-AGC的设计初衷不相符，所以需对KFF-AGC方法采取进一步改进。

图1 出口厚差曲线Fig.1 Export thickness difference curve

1 影响板带厚度的因素分析

在生产实践中，可将影响出口带钢厚度的因素分为两类：一类是轧机内部的扰动，另一类是轧件本身产生的扰动。轧机内部的扰动有：轧辊热膨胀、轧辊偏心、轧辊磨损、油膜厚度等。轧件产生的扰动有：轧件入口厚度不均匀、轧件加热不均产生水印、机架间张力变化等。在热连轧生产过程中，还有一个重要的工艺参数——轧制温度。由于轧制温度会直接影响到轧制力的大小，因而精确预测轧机各机架的轧制温度是保证成品带钢出口厚度达到目标的关键。一般情况下，硬度K与温度T相关。金属材料的硬度K在钢种确定的情况下，主要取决于轧制温度T、变形速度v及变形程度e，可以用

如果来料因为一定的温度波动而产生硬度波动，那么这段带钢每进入一个机架都会产生一定的硬度波动，致使钢板每经过一个机架后，都会产生厚度波动，这些厚差也会同样影响到后面几个机架的出口厚度。由此可知，在轧制过程中，温度的波动会引起带钢硬度波动，进而影响每一机架的出口厚度发生变化，最终导致出口带钢的厚度精度较低。这种重复发生的现象会严重影响成品带钢的质量。虽然热连轧机具有削减来料厚差的能力，但无法消除由于温度波动引起的厚差。因此，需要根据温度波动引起的硬度波动，调整对带钢轧制产线的控制策略，提升出口带钢的厚度精度。

2 前馈控制

2.1 前馈控制基本思想

轧机自动厚度控制系统采用直接或间接的测厚AGC。由于热轧生产线中的测厚仪的实测数据存在滞后情况，用于带钢的厚度的反馈控制时容易引起较大误差，所以高速轧制时的板厚精度将会受到制约。前馈控制克服了控制系统本身的惯性，控制效果更好。因此，前馈控制能够减少带钢头端部鼓包、水印和尾端部尖峰等状况的发生。

前馈AGC的主要功能是将本机架的实际出口厚度偏差，用于下一机架的预先调整，减小对下一机架出口厚差的影响，实现获得目标轧出厚度。图2可以用来说明前馈AGC的必要性。图2（a）表示具有阶跃形的轧件咬入轧机后，在反馈AGC作用下厚差的变化。由于系统存在滞后时间ΔT2，加上压下移动需要一定的时间ΔT1，因而在轧件的一段长度上有较大的波动；图2（b）表示无超前量前馈AGC的动作过程；如果将前馈控制量提前某一合适的时间ΔT送出，则可以得出图2（c）所示的结果。在所有的AGC系统里，只有前馈AGC可以采用这种提前控制的方法。

图2 前馈控制效果示意图Fig.2 Schematic diagram of feedforward control effect

图2中，H和h分别代表机架的入口厚度和出口厚度。根据影响系数分析法可知，造成热轧带钢厚差的主要原因是带钢全长的温度不匀产生的硬度波动。由于硬度波动具有重发性，因而可以利用F1机架作为硬度检测机架对下游机架进行前馈控制。该机架不参与AGC调节，保持恒辊缝。

2.2 前馈控制基本算法

前馈控制思想的基本方程为Fi（i=1～6）机架出口厚度的变化量和轧制力变化量方程，可用下式来表示：

式中：δ代表偏差；i表示F(i)（i=1～6）机架；δhi为i机架出口厚差；δPi为轧制力偏差；δHi为i机架入口厚度变动（从静态角度可以认为δHi=δhi-1）；δKi为第i个机架入口硬度变动；δSi为i机架的辊缝调节量；M代表刚度系数；Q代表塑性系数。式（4）中的AXi对应式（2）中的AHi、AKi、ASi，当AXi取AHi、AKi或ASi时，Xi则为(∂P/∂H)i、(∂P/∂K)i或M；式（5）中 的BXi对 应 式（3）中的BHi、BKi、BSi，当AXi取BHi、BKi或BSi时，Xi则 为(∂P/∂H)i、(∂P/∂K)i或M。

求取δKi时，由于F1机架不投入AGC，故δSi=0，其轧制力波动是由δHi、δKi所产生的：

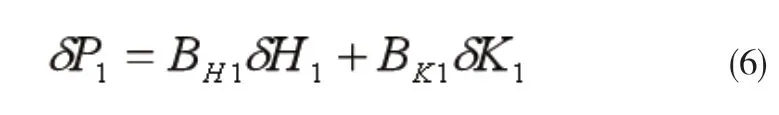
在粗轧末架采样轧制力以获得粗轧出口厚度δh0，则可得：

计算δKi时，当精轧入口温度有变动时，不能用(δK/K)i相 等 的 法 则，即 (δK/K)1=(δK/K)2=…=(δK/K)6来表示各机架δKi间的关系，而是应该采用式（8）的方法表示各机架的硬度关系：

式（8）中：βi为F(i)（i=1~6）机架的比例系数。当然，面对不同的模型时，计算的结果也会不同。计算时以设定出口温度TR来计算各机架的轧制温度，并由此计算出轧制力及设定辊缝。然后，假设TF0有一个大小为δT的温度变动，计算出此时温度状态，进入设定辊缝后将产生的hi、Ki及Pi。从而可计算获得δKi：

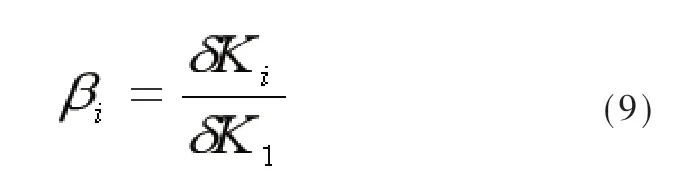
为使F2机架的出口厚差为零，计算可得：

为了使F3～F6的出口厚差为零，辊缝调节量的计算方式如式（12）所示：

热轧带钢产生厚差的主要原因是因入口温度不同而导致带钢硬度不同，而不是因为带钢的入口厚度不同，硬度前馈AGC是根据带钢硬度进行前馈而不是根据厚度。式（10）是用来消除F1、F2机架因硬度不同而使F2机架产生的出口厚差，由于F1机架不参与调节，前两个机架的厚差消除工作实际上均由F2机架来完成。式（12）是消除下游F3～F6机架因硬度不同而产生的相应机架的出口厚差。根据硬度前馈的思想，即使上游机架不能完全消除出口厚差，也不影响下游机架AGC调节量的计算方式。

3 某钢厂KFF-AGC系统

KFF-AGC策略的优势在于不会产生滞后现象，甚至在一些情况下还可实现对带钢的超前控制。在某钢厂1700mm热连轧上使用KFF-AGC，理论根据是：在热轧工艺条件下，来料厚度波动比较容易消除，而且不具有长期的遗传性。恰恰相反的是，由于温度波动造成的来料硬度波动对于出口产品的厚度质量影响很大，而且硬度波动在各机架轧制过程中具有很强的遗传性。为此，在F1机架上不执行任何AGC功能，将F1机架当作一台前馈硬度测量机架，利用轧制压力的在线测量而计算出板坯的硬度波动情况，系统根据硬度的波动情况计算出F2～F6各机架的硬度前馈投入方式和控制率，然后根据计算得到的投入方式和控制率调整下游机架的设定值，如图3所示。这种利用F1机架作为检测机架去控制下游机架的方式与 Hatch Steltech相似，但Hatch Steltech采用的是压力前馈。

图3 某钢厂1700mm热连轧KFF-AGC控制方案Fig.3 KFF-AGC Control scheme for a 1700mm hot strip mill in a steel mill

实践表明，仅几个机架采用这种厚度前馈并不能解决成品厚差。这是由于真正造成轧制力变化（轧出厚度变化）的是该段带钢温度偏低（或偏高），这种温度变化在该段带钢进入每一机架时都将发挥作用，产生厚差。因此，应在F1机架检测出这种温度变化（实质为硬度变化）。以此硬度变化为出发，对后面每一机架进行前馈控制，这便是KFF-AGC的基本思想。

前馈AGC的计算公式为：

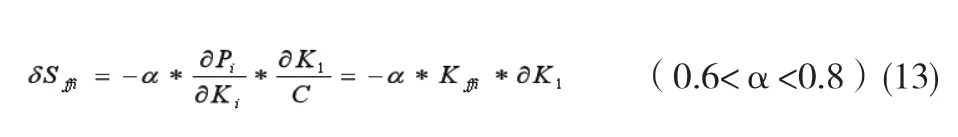
式（13）中：δSffi代表前馈AGC补偿量；C为轧机的刚度系数；α的取值不等于1的原因是考虑到轧辊偏心的影响；Kffi为第i个机架的硬度前馈压下效应系数。硬度前馈压下效应系数，可通过实际调试予以确定。

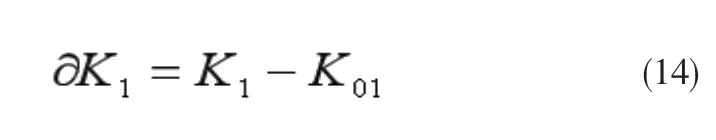
式（14）中：K1、K01分别为F1机架的实际硬度和目标硬度。

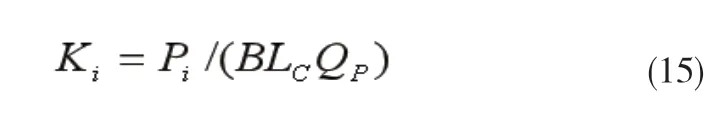
式（15）中：Pi为轧制力大小；B为轧件宽度；Lc为接触弧水平投影长度；QP为外摩擦状态系数。

式（16）中：R为工作辊的辊径；h0、h分别是入口厚度和出口厚度。

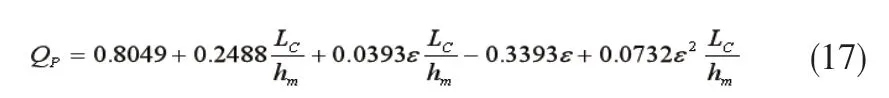
式（17）中：hm为轧机入口厚度h0与出口厚度h的平均值；ε为相对变形程度。即：

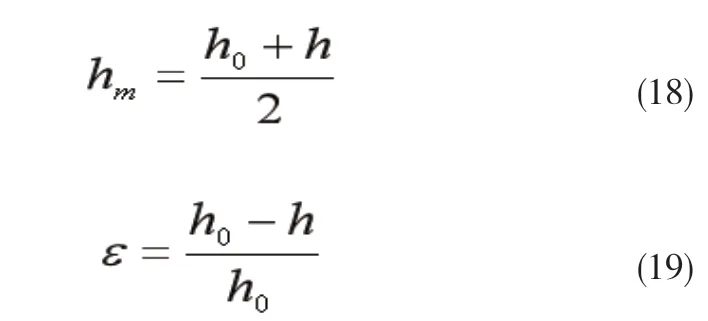
4 KFF-AGC存在的问题及对策

虽已有不少文章提出偏心补偿的方法，但现阶段仍不能有效去除轧辊偏心对带钢质量的影响，故而式（13）中α小于1是必然的。但正是因为此α的存在，导致了KFF-AGC没有真正消除趋势性厚差和突变性厚差。趋势性厚差可由随后的MN-AGC来消除，但如果厚差过大，会加重F6机架MN-AGC的负担，甚至导致F6机架AGC调节量饱和，最终影响到精轧出口厚度精度。而突变性厚差不能被GM-AGC有效消除，这是因为检测仪表和执行机构都需要响应时间（大于50ms），GM-AGC检测和控制的又不是同一位置，这会导致突变性厚差在出口厚差中仍比较明显，造成了图1所示出口厚差的多个鼓包。

针对这一情况，如图4所示，可以把F1检测到的硬度信息K1（曲线AE）分为趋势性硬度K1T（直线AD）和突变性硬度K1S（曲线AC）。趋势性硬度不含轧辊偏心干扰，用KFF-AGC进行控制时可以取α=1。这样就只剩下突变性硬度K1S，对包含轧辊偏心信号的K1S用MFFT方法滤波，就可消除大部分偏心信号和随机波动[4]，这时用KFFAGC方法控制便可按照图5所示的二次函数对α进行取值。图5中的Kα初值在2.0×10-4（T/mm2）附近，可以通过反复学习控制加以改进[5]，反复学习控制框图如图6所示。图中，uk表示Kα第k次迭代参考输入；yd为有界连续期望输出；yk为出口厚差精度百分数的第k次迭代输出；ubk为反馈信号；ek为偏差；Δuk为修正信号。

图4 硬度信息分类示意图Fig.4 Schematic diagram of hardness information classification

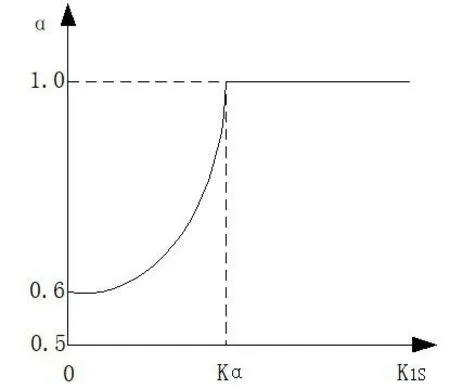
图5 突变性厚差控制中α的取值Fig.5 The value of α in the abrupt thickness difference control

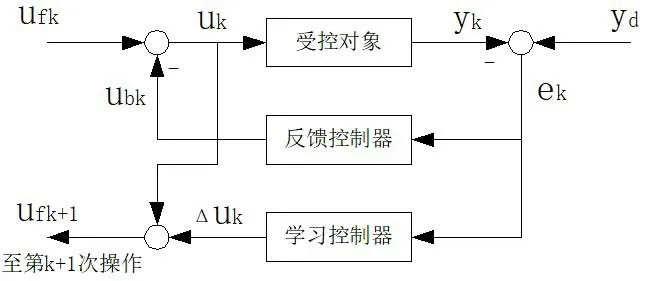
图6 反复学习控制Fig.6 Repeated learning control

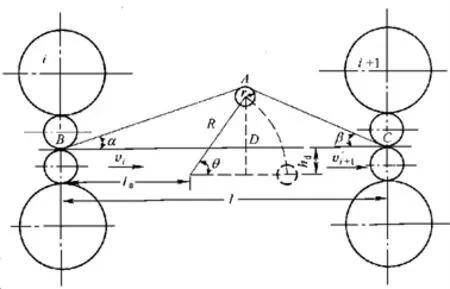
图8 活套参数示意图Fig.8 Schematic diagram of looper parameters

图4所示的只是硬度信息分类的示意图。实际上，由于带钢头尾厚跃的缘故，用最小二乘法进行直线拟合时，只能对带钢本体部分进行估计（图7中BC段虚线），带钢头部的趋势性硬度则需利用前一块钢的硬度信息进行估计（图7中AB段虚线），带钢尾部的趋势性厚度则利用BC段硬度信息所拟合的直线延长得到（图7中CD段虚线）。BC段虚线之所以不是直线，是因为F1采集数据和对F2～F6机架进行控制是同时进行的。由于F1机架采集的数据是不断增多的，拟合的直线也就会不断变化。

图7 KFF-AGC的改进策略Fig.7 The improvement strategy of KFF-AGC

F1机架检测到某点的硬度信息，当该点进入F2～F6时，各机架应进行相应动作，可以用式（20）来计算该点进入下一机架的时间。

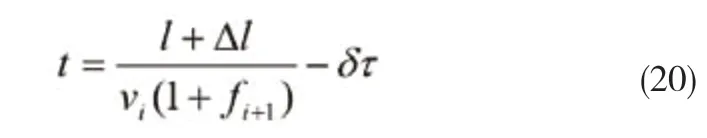
式（20）中：l为机架间距离；Δl为套量的变化量；vi为上游机架出口速度；fi+1为下游机架的前滑值，可根据前一机架的压下量计算得出[2]；δτ为系统响应延迟时间，可通过对上一块钢的AGC给定和位置反馈数据进行FFT变

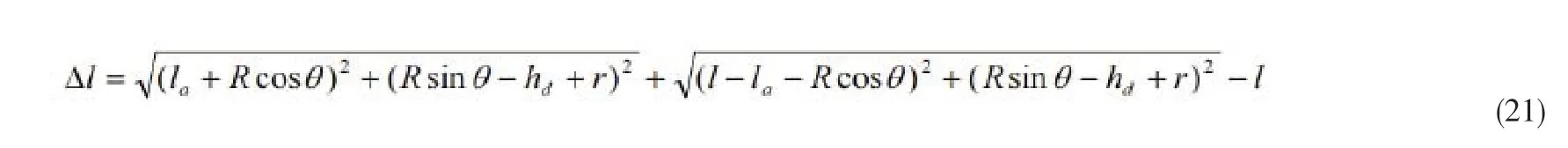
对于速度补偿采取的是后架补偿的方法[6]：

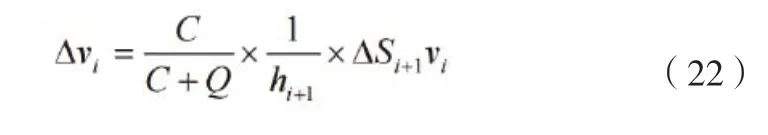
式（22）中：Δvi为F(i)机 架 由 于F(i+1)机 架AGC调节时的速度补偿量；C为轧机刚度系数；Q为轧件塑性系数；hi+1为F(i+1)机架的厚度设定值；Si+1为F(i+1)机架的辊缝调节量；vi为F(i)机架速度设定值[6]。

5 结论

在轧制同一种规格的钢种时，将改进后的KFF-AGC方案应用于轧制产线，出口厚差的曲线如图9所示。将之与图1对比分析，可以看出带钢出口厚度的精度有明显提升。改进后的KFF-AGC可以保证带钢全长的97.5%以上落在±50µm厚差范围内。因此，可得出结论即本文提出的改进KFF-AGC方案是可行的。对其他类型的AGC来说，亦存在厚差消除效果不明显的相似问题，本文所提出的解决方案值得其他类型AGC借鉴。

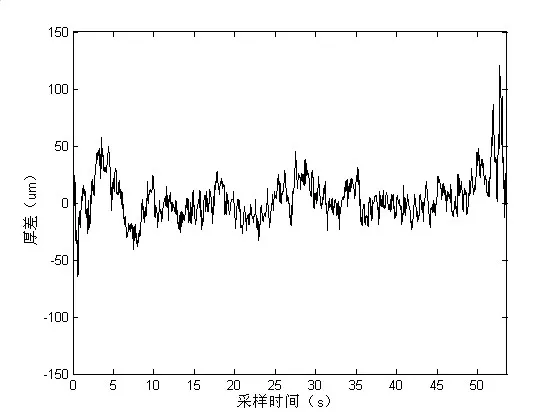
图9 改进后的KFF-AGC控制效果Fig.9 Improved KFF-AGC control effect