基于模式转换的电磁超声螺栓轴力测量*

王文军, 丁 旭, 饶 刚

(武汉科技大学 机械传动与制造工程湖北省重点实验室，湖北 武汉 430081)

0 引 言

通常来说，螺栓连接的可靠性取决于螺栓的预紧力，即螺栓的轴向应力，简称轴力。针对传统螺栓轴力测量方法的困难和不足，近年来一些学者将超声无损检测技术应用到螺栓轴力的测量中，并取得了一些成就，而电磁超声传感器的应用克服了压电超声使用耦合剂的缺点[1]，但电磁超声传感器的信号比较微弱。对此，巴洪等人[2]提出一种增强传感器信号的方法并得到了验证。而螺栓轴力的超声无损检测原理主要是基于材料的声弹性效应[3]，声弹性应力测量技术中最具有代表性的方法是脉冲纵波相对测量法，其通过计算螺栓加载前后的声时差乘以声时差—应力系数得到轴向应力。然而，由于该方法必须事先得知螺栓的初始渡越时间及其等效受力长度，故无法用于测量已紧固螺栓的紧固力[4]。Yasui H等人[5]提出利用纵横波渡越时间比值法来解决这一问题，虽可以测得螺栓轴力，但在在实际应用中，纵波和横波换能器的耦合条件(安装位置、按压力、耦合剂浓度等)必须尽量相似才能保证其测量精度，故实用性不佳。

通常使用的声时测量方法的精确度易受信噪比影响，为实现高测量精确度需要进行大量平均抑噪，测量时间长，效率低。邹晓红[7]将小波分析应用到超声信号的处理当中，发现其可以提高信号的检测和特征提取，提高了信噪比。王萍等人[8]利用互相关算法精确地测出了超声波的传播时间。丁旭等人[9]提出了基于互相关法的声时提取方法，并且发现该方法具有较强的噪声抑制能力，但是互相关需要两路信号才能计算。

本文提出了单探头横波换能器的超声轴力测量原理，其具有高灵敏度、通用性强等优势，并且对螺栓本身的要求也低，非常适合用于螺栓轴向应力的测量[6]。本文结合互相关理论和测量所得信号的波形图，提出了一种简单的声时提取方法。

1 超声波的模式转换

根据超声波在介质中的传播特性，当电磁超声换能器(electro-magnetic acoustic transducer,EMAT)在螺栓端面激励产生与端面法线成微小夹角的横波，横波在另一端面反射，发生波型转换，产生一束横波和一束纵波被超声探头接收，而超声波在端面发生波形转换的现象称为超声波的模式转换现象，转化产生的波称为波型转换波[10]。超声波在螺栓中的传播路径如图1所示,其中将螺栓简化为理想圆柱体；图中，S1为入射横波传播路径，S2为反射横波传播路径，S3为反射纵波传播路径，α为入射横波发射角，θS为入射横波入射角，γS为反射横波反射角，γL为反射纵波反射角。在实际计算时，由于横波与轴线的夹角非常小，可以将超声波的传播路径近似视为沿轴线传播。

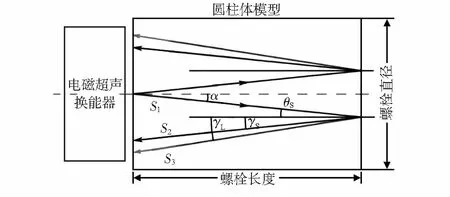
图1 超声波在螺栓中的模式转换

根据声波的反射原理，由Snell定律可知，超声波在图1所示的传播路径满足如下的关系式

α=θS

(1)

θS=γS

(2)

(3)

式中CS为螺栓中横波声速，CL为螺栓中纵波声速。

假设螺栓预紧后的的长度为L，可以得出横波以及波形转换波在螺栓的传播时间，根据图1，其计算方法可以表示为

(4)

式中T1-2为S1到S2的传播时间，T1-3为S1到S3的传播时间。

2 螺栓轴力测量原理

螺栓的轴力可以通过测量螺栓轴向应力获得，而螺栓轴向应力可通过螺栓中声弹性效应产生的声速变化进行测量。由声弹性效应可知螺栓内部的声速会随着应力状态的变化而变化

(5)

式中CL,CL0分别为螺栓受应力和不受应力时的纵波声速；CS,CS0分别为螺栓受应力和不受应力时的横波声速；σ为应力大小；λ，μ为二阶弹性常数；m为三阶弹性常数。

式(5)可简化为

(6)

其中

(7)

式中kL为纵波声弹性常数，kT为横波声弹性常数。由式(6)可知，声速随应力状态变化。

根据胡克定律可知在物体的弹性范围内，应力与应变满足正比例的关系。所以有

(8)

式中E为材料的杨氏模量，L0为代表螺栓全长，Lσ为螺栓等效受力长度，即螺栓受到应力时分布近似均匀部分的长度。

在实际计算时，由于声速变化量难以直接获取，故常以超声波的渡越时间代替。纵波和横波的渡越时间可表示为

(9)

式中TL为纵波渡越时间，TS为横波渡越时间。将上下两式相除后，整理得

(10)

其中

由式(10)可知，只要确定横波与纵波的渡越时间比，以及与材料属性相关的参数a，b和c，就能计算出轴向应力σ。显然，要保证螺栓轴力测量准确性，最重要的是声时的测量精度。必须指出，温度变化对超声波传播速度有较大的影响[11]，应尽可能保持恒温下进行螺栓轴力的超声测量。

3 互相关时延估计

基于相关的时延估计是最经典的时延估计方法，其中心思想是通过对两个信号相似性的比较，可以快速、准确的获得时间延迟，并且具有较强的噪声抑制能力。对于超声传感器接收到的信号x1(t)与x2(t)，s(t)为源信号，D为时间延迟，n1(t)和n2(t)分别为接收信号的噪声，它们相互独立。假设信道的衰减因子为l，则接收的超声信号的模型为

x1(t)=s(t)+n1(t)

(11)

x2(t)=s(t-D)+n2(t)

(12)

则互相关可以表示为

R12(τ)=E[x1(t)x2(t-τ)]=Rss(τ-D)

(13)

式中Rss(τ-D)为s(t)信号的自相关，由于自相关满足Rss(τ-D)≤Rss(0)，所以，τ=D时，互相关函数取最大值，即互相关的估计问题可以表示为

(14)

4 螺栓实测信号的处理

实验使用如图2的螺栓轴力电磁超声测量系统，由右边的电磁超声发生系统和左边的轴力加载系统组成。超声系统由电磁超声探头、个人电脑PC、电磁超声检测仪组成，轴力加载系统包括轴力加载测试台和轴力显示系统。螺栓试件规格为M24×150的10.9级高强度六角螺栓，其材料为35VB。为排除温度对材料声速的影响，实验室保持恒温，使用螺栓轴力台对样件进行轴力加载，记录下每次测量的数据。

图2 螺栓轴力电磁超声测量系统实验台

如图3为首次测量的超声信号波形结果，从螺栓测量结果波形图可以看出：第一次横波与第二次的横波回波，并且可以看出第二次回波的幅值相比较第一次的回波幅值发生衰减，而且只能通过两次的回波时差粗略得出横波的声时，但是并不能得出模式转换纵波的声时，必须对测量所得的信号进行一系列的信号处理，以便计算出较为准确的声时。

图3 首次测量的波形结果

根据数字信号的处理原理，观察实验测得信号波形图，首先使用巴特沃斯滤波器对测得的信号进行滤波，本文将测量所得的信号导入MATLAB软件中，选取采样频率为50 Hz，使用MATLAB巴特沃斯滤波器函数对信号进行高通滤波处理，其中滤波器阶数取4，根据实验的激励信号，截止频率取500 kHz，处理后的结果如图4所示。

图4 滤波后波形

根据互相关时延估计的原理，对滤波后的结果作自相关得图5。根据螺栓长度和钢铁材料上纵波公称声速，计算出波型转换波应出现在79.3 μs左右处，并且发现自相关之后的此位置一个回波信号，峰值约为0.107，说明可以得出信号的波型转换纵波。求其包络峰值处对应的时间，即可得到回波对应的声时。

图5 自相关后的信号

通过拧紧螺母对螺栓进行轴力加载，螺栓受到的拉力将显示在图2左侧的显示屏上。每间隔25 kN的轴力加载，记录一次测量数据，直到螺栓拧不动，一共记录下测量数据11组，螺栓轴力依次从0加载到了250 kN。

根据本文提出的模式转换的螺栓轴力测量原理，以第一次和第二次的横波回波声时差作为横波的声时，以第一次横波回波与波形转换信号的时间差作为纵波的声时，可得纵横波的声时比值，分别对记录的11组数据做相同处理，最终得到波型转换纵波和横波的声时比与轴力的关系如图6。将声时比和轴力的关系进行线性拟合，得到两者的关系为

图6 声时比与螺栓轴力关系

RL-S=6.376×10-5F+4.496

(15)

其中,轴力F的单位为kN。线性回归的判定系数R2=0.994 5。

5 结束语

本文提出了一种基于超声波波型转换的电磁超声螺栓轴向应力的测量方法。使用电磁超声横波换能器，通过超声波在螺栓端面发生反射产生波型转换，同时接收横波和纵波。通过对超声波反射线路的分析，建立了螺栓轴向应力测量模型。为验证方法测量螺栓轴向应力测量方法的有效性，进行了螺栓轴向拉力测量实验，并基于互相关的时延估计原理对测量信号进行数据处理，结果表明：螺栓纵波与横波飞行时间之比与螺栓轴向拉力成线性关系。使用该方法测量螺栓轴力具有非接触特性，并且测量方便、快捷。