基于改进即时学习的海洋碱性蛋白酶菌体浓度广义预测控制*

朱湘临, 蔡 可, 王 博

(江苏大学 电气信息工程学院,江苏 镇江 212013)

0 引 言

由于微生物发酵过程具有较强不确定性,且其内部机理复杂多变,一般难以建立准确的机理模型[1～4]。采用传统的控制策略优化补料速率很难达到预期的效果,因此有必要研究新型的优化控制策略[5～14]。广义预测控制(generalized predictive control,GPC)具有鲁棒性强、控制效果好的优点,它拥有预测控制算法中的滚动优化、多步预测、反馈校正等步骤。其中影响GPC控制精度最重要的部分是预测模型。最小二乘支持向量机(least square support vector machine,LS-SVM)[13]能简化计算复杂度,特别适用于在线建模，但它通常是基于全局模型的建模技术,而发酵过程是多工况的,仅仅建立单一的全局模型,预测精度往往较低。即时学习(just-in-time learning，JITL)是一种局部在线建模策略,它充分发掘了历史数据库中数据之间的信息,适合发酵过程的建模[11]。考虑到历史数据库信息量大和发酵的时段性特点,采用加权模糊C均值(weighted fuzzy C mean,WFCM)算法[13,14]对数据库进行聚类,当查询样本到来时能快速选择相似样本集建立预测模型。

基于以上分析,本文提出了基于LS-SVM和改进JITL策略相结合的预测模型,同时为了避免预测控制中求解非线性问题,将得到的非线性模型在每一个采样点处进行线性化,再融合GPC控制算法,建立菌体浓度的GPC模型。通过仿真结果表明这种控制方法在海洋蛋白酶的流加补料控制中具有良好的控制效果。

1 菌体浓度预测模型建模分析

通过对海洋碱性蛋白酶化学特性和发酵工艺流程的深入分析,碳源葡萄糖是其菌体生长的重要基质。本文选取葡萄糖给进速率u(t-m)与前一时刻菌体浓度值y(t-n)为输入量,以及当前时刻的菌体浓度输出y(t)为输出量。海洋碱性蛋白酶菌体浓度模型可用非线性形式表示

y(t)=f(u(t),u(t-1),u(t-2),…u(t-m),

y(t-1),…,y(t-n))

(1)

式中f(·)为复杂的非线性函数关系。

2 基于改进JITL的LS-SVM预测模型建立

对于一组输入样本,LS-SVM利用非线性映射将训练数据集非线性的映射到高维的特征空间,从而使非线性函数估计问题转换为线性函数估计问题。设建模数据集Ω={x1,x2,…,xn},xi是查询样本周围包含的n个相似样本,利用LS-SVM算法将相似样本集映射到高维线性特征空间,并构建最优回归函数如下

(2)

式中ci为拉格朗日乘子,δ为偏置量,采用高斯径向基函数exp{-‖x-xi‖2/2σ2}作为核函数。

3 改进JITL策略

传统的JITL策略在搜寻相似样本时,需要对整个数据库进行搜索。考虑到发酵过程的历史数据量较大,就海洋碱性蛋白酶发酵为例,一个完整的发酵周期通常为200 h,随着发酵批次的进行,历史数据会越来越多。因此需要采取一种选择策略加速相似样本的选择。鉴于微生物发酵的一般特性：时段性,本文采取WFCM对收集的数据进行分类,当查询值到来时,首先先确定它属于哪一个时间段,再使用相似度度量准则确定相似样本集。这样不仅能加速样本集的确定,而且缩小了样本选择空间,减少噪声数据的干扰。

3.1 WFCM聚类

WFCM聚类算法属于非监督学习方法[13,14],根据数据本身之间的特性将数据分为几个类别,同一类别中数据具有较高相似度,反之亦然。它能够很好地处理差别较大的数据集,适合对发酵历史数据进行聚类。

假设X={x1,x2,…,xn}为有限数据集,数据集的维度为p,xk∈Rp为第k个样本的特征向量。类别数c可以为任意值(2≤c≤n),则数据集的WFCM聚类问题可归结为求解以下数学问题

(3)

式中pi为样本的权系数,pi的大小直接关系分类的影响程度。dij=‖xi-Vj‖为样本点与聚类中心的距离。uij为第i个样本属于第j个中心的隶属度,U为n×c的模糊划分矩阵。V=[V1,V2,…,Vc]为c个类别的向量集；m为用来控制聚类的模糊加权指数。

为了求解上述数学问题,将拉格朗日乘法引入

(4)

式中pi主要用于调节聚类中心的距离大小。

3.2 相似度度量准则

本文采用基于角度和距离加权的相似度选择指标[5,6]。定义查询样本点xq和所处发酵阶段中任意样本xi的距离和角度表示如下

(5)

式中λ为权值,si的取值介于[0,1]之间,其值越大,表示xq与xi越相似。当cos(θi)<0时认定该数据相似度较低,不予采用。

4 菌体浓度的GPC算法

GPC[11]是由Clarke等在保持最小方差自校正控制的模型预测、最小方差控制、在线辨识等原理的基础上提出来的,它采用带控制量的自回归积分滑动平均(controlled autoregressive integrated moving average,CARIMA)模型作为预测模型。

4.1 基于JITL-LS-SVM的预测模型线性化

上述得到的JITL-LS-SVM模型是非线性的,不能直接用在GPC系统中,需要对模型线性化。考虑到海洋蛋白酶发酵这样的非线性系统可以用如下线性时变系统表示[12]

y(t)=a1y(t-1)+a2y(t-2)+…+anyy(t-ny)+

b1u(t)+b2u(t-1)+…+bnuu(t-nu)

(6)

在采样点x0处利用泰勒公式展开。线性化后的模型为

A(z-1)y(t)=B(z)u(t-1)+∂

(7)

式中A(z-1)=1+a1z-1+…+anz-n,B(z-1)=1+b1z-1+…+bmz-m,∂为常数。上式与GPC算法中的CARIMA模型形式基本吻合,考虑到发酵这样的强时变性,存在的不确定因素较多,对模型进行进一步的修正

(8)

式中ω(t)为白噪声,C(z-1)=c0+c1z-1+…+cncz-nc,nc为系统的扰动阶次,当C(z-1)=1时,系统为一阶时滞。

4.2 菌体浓度的GPC算法

对上述线性化处理后的模型进行转换,将常数∂消除并离散化,得到如下的CARIMA模型为

(9)

式中y(t)为系统输出量,即菌体浓度；u(t)为模型输入；Δ=1-z-1为差分算子；ε(t)为系统噪声影响量。采用一般的GPC方法继续对式(9)处理,引入Diophantine方程求解,求解后可以得到多步预测后的矩阵输出形式

(10)

F=[F1(z-1)F2(z-1)Fp(z-1)]T；

H=[H1(z-1)H2(z-1)Hp(z-1)]T

t时刻的滚动优化表达形式如下所示

(11)

式中E为期望,w为菌体的期望参考值,N1和N2分别为优化时域的初始值和终值,λ(j)为控制加权系数,一般设为常数λ。为确保输出值能够较好跟踪参考轨迹,将参考轨迹引入其中

w(t+j)=βw(t+j-1)+(1-β)×ys,j=1,2,…,N

w(t)=yr(t)

(12)

式中β为调节因子,范围为[0,1)之间;yr为参考轨迹;ys为将来某时刻的设定值。令W=[w(t+1),…,w(t+P)]T,则有

J=(Y-M)T(Y-W)+λΔUTΔU

(13)

当∂J/∂U=0时,可以得到控制律为

u(t)=u(t-1)+dT(W-F)

(14)

式中dT为(GTG+λI)-1GT的第一行。

基于JITL-LS-SVM的海洋碱性蛋白酶菌体浓度的GPC框图如图1所示。

图1 基于JITL-LS-SVM的海洋蛋白酶菌体浓度的GPC框图

图1中yr为菌体浓度设定值,y(t)为菌体浓度输出值,y(t+1)为t+1时刻的预测值。在t时刻,GPC根据yr和JITL-LS-SVM预测模型输出的对象预测输出值y(t)来计算输出控制量u(t),将控制量u(t)输入到基于JITL-LS-SVM的预测模型和被控对象中,JITL-LS-SVM预测模型根据Nx前个控制量和前Ny个输出值来得到下一时刻的预测输出值y(t+1)。将y(t+1)返回到GPC,进行下一时刻的控制。

4.3 基于JITL-LS-SVM的GPC算法实现步骤

基于以上分析,本文将LS-SVM算法,改进的JITL算法融入到基于CARIMA模型的GPC算法中。具体算法实现步骤如下：1)基于海洋蛋白酶发酵过程,构建历史数据库。设定GPC模型参数P、M和LS-SVM的C、σ。采用WFCM算法对历史数据分类,并设定类别数c和模糊加权指数m。2)针对当前工况时刻点,判定所属发酵阶段类别,采用式(5)的相似度度量准则,选择相似样本构建局部建模样本集。3)利用相似样本集建立基于JITL-LS-SVM的局部预测模型。4)引入GPC算法,根据参考轨迹来计算控制增量Δu(t)和控制律u(t)；输入u(t)到JITL-LS-SVM 预测模型和被控对象中,得到y(t)。根据u(t)和y(t)得到预测值y(t+1)。5)t→t+1,返回步骤(2)。

5 实验与结果分析

实验数据来自江苏大学发酵控制系统平台。选用镇江日泰发酵设备公司RTY-MS型号的20L发酵罐,选用从中国黄海水样中分离得到的菌株YS-9412-130(主要分泌碱性蛋白酶)为菌种。按照发酵工艺流程进行发酵并收集数据。依据上位机每隔1 min采集葡萄糖流加速率,菌体浓度每隔2 h离线化验所得,在实际建模中采用1 h插值运算。一个发酵周期取一批数据,共提取10批数据,每个批次取发酵前80 h,一共收集800个样本,剔除噪声数据后,将剩余的768组数据中的80 %作为训练集,20 %作为验证集。

将LS-SVM模型和JITL-LS-SVM模型分别融合GPC构建预测控制模型。 在产酶加速期和高峰期,细胞呈对数增长,对该时期的菌体浓度进行有效控制可以提高酶的活性和产量。选取发酵中期的对数生长期(10～40 h)进行GPC,预测时域P=5,控制时域M=3,设初始输出u=15,初始增量Δu=4.5,初始输出为y=14.5,仿真步长为15 min。设定值为给定的方波信号,依据在对数期的前段时间处于产酶加速期,菌体浓度不宜过高,将其设定为20 g/L。后段时间处于产酶的高峰期但由于前面时刻基质消耗比较快,菌体生长速度减慢需要加快基质给进速率,并将菌体浓度设定为33 g/L以提高酶的活性和产量。

由图2的仿真中可以看出,基于LS-SVM的GPC输出虽然能大致跟踪设定值,但是超调量较大。而基于JITL-LS-SVM的GPC输出较好地跟踪参考轨迹且输出较平稳,超调量小。

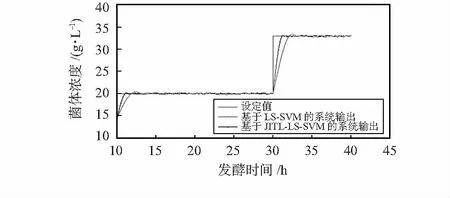
图2 海洋碱性蛋白酶菌体浓度的仿真跟踪控制曲线

图3为基于JITL-LS-SVM的GPC模型下的葡萄糖给进速率图,可以看出每个时刻的速率都是变化的。由此可见基于JITL-LS-SVM的GPC方法是可行的。

图3 基于JITL-LS-SVM模型的补料速率输出仿真曲线

图4为海洋蛋白酶发酵过程中菌体浓度真实值与基于LS-SVM和JITL-LS-SVM的GPC模型的效果对比。

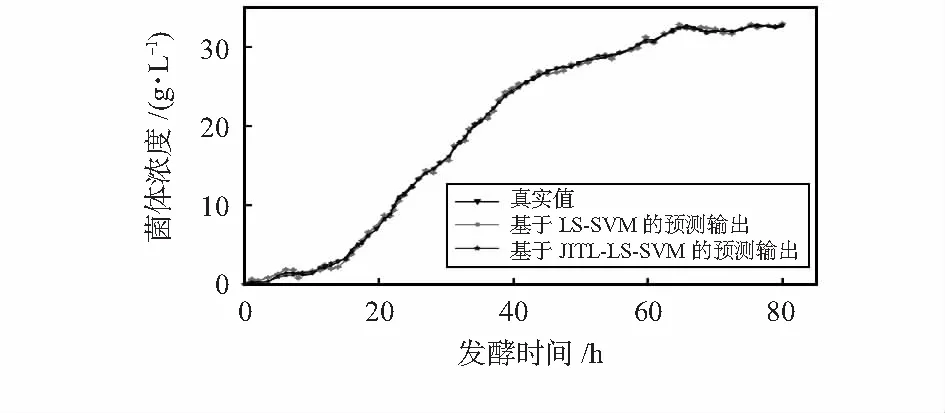
图4 系统实际输出对比

图5为误差对比图。从图5中可以看出基于JITL-LS-SVM的GPC在拟合程度和预测精度上明显优于LS-SVM的GPC模型。其中模型参数采用交叉验证法获得,取LS-SVM参数C=106,σ2=4.6。WFCM的类别数c=3,模糊加权指数m=1.9。

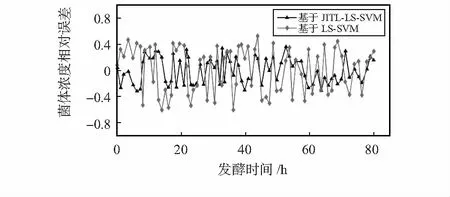
图5 系统误差对比

选取均方根误差(RMSE)和最大绝对误差(MAXE)作为模型精度评价标准。如表1所示,基于JITL-LS-SVM的GPC的控制输出效果更加好,菌体浓度更加逼近真实值

表1 二种预测模型效果对比

(15)

6 结 论

本文提出的一种改进JITL策略的GPC补料方法,利用WFCM算法和基于角度和距离的相似度准则,加速相似样本的选择,并建立菌体浓度的JITL-LS-SVM非线性控制模型。为了避免求解非线性问题,将预测模型在每一个采样点处进行线性化,并融合GPC算法。通过仿真验证方法对海洋蛋白酶发酵过程中菌体浓度控制具有很好的自适应和鲁棒性,可以运用于一般微生物发酵中的流加补料控制。