步进电机S型加减速算法改善研究
刘锦杭
(惠州城市职业学院 机电学院,广东 惠州 516025)
0 引言
步进电机的加减速控制一直是影响电机运行的重要因素,突变的加减速会导致电机失步,造成位置与精度误差,因此必须有合理的加减速控制来保证电机能够平稳顺畅地运行。电机的运行是一个“加速-恒速-减速-停止”的过程,在此过程中,当控制系统极限启动频率大于电机所需运行速度时,电机可以直接启动;当控制系统通过停止发送驱动脉冲或让使能离线时电机停机。若在电机启动时,直接以正常运行速度启动,容易导致电机失步或无法启动。为了避免此情况,电机启动后需要有一个均匀加速的过程来慢慢达到要求的运行速度。另一方面,由于惯性的存在,电机停止容易冲过设定的目标位置,造成位置偏离,正常的电机停止应该使启动速度等于或略高于减速过程结束时的速度,经低速运行若干步后停止。为保证步进电机运行的稳定、平滑,本文从电机的加减速控制算法入手,通过改善S型加减速算法来实现电机的稳定运行,并通过MCU控制器对运行过程进行仿真,以验证改善后的S型加减速算法的可行性。
1 电机加减速控制方法分析
目前对电机加减速的控制主要有T型加减速算法和S型加减速算法,如图1、图2所示。图2中,c为加加速度,是一常数;0~t1时间段为加加速阶段,速度由起始速度增加到中间速度v1,加速度a逐步增加;t1~t2时间段为减加速阶段,速度由v1上升到运行速度vt,此时间段内加速度a减小到零,加加速度为负值;t2~t3时间段为均速运行阶段;t3~t4、t4~t5分别为加减速阶段和减减速阶段,与加速曲线对称,两时间段内加速度a为负值。对比两种控制方式在启动瞬间、加速结束、开始减速、减速完成四个节点的情况,T型加减速算法在加减速过程中角加速度突变不连续,导致角速度ω不能平滑过渡,而S型加减速算法在加减速阶段与匀速阶段都是连续的,且加速度的变化率是可控的,这有利于电机控制性能的提高。但是相对来说,T型加减速算法容易实现,而S型加减速法算法比较复杂。

图1 T型加减速算法曲线

图2 S型加减速算法曲线
2 S型加减速算法改善
基于对两种算法的分析,S型加减速算法有利于提高步进电机的运动稳定性,避免机器运动时造成的柔性冲击,本文对S型加减速算法进行研究。S型曲线来源于Sigmoid函数,是一个在生物学中常见的S型函数,其定义为:
(1)
曲线方程(1)将横坐标的任一实数映射在(0,1],如图3所示,曲线平滑,能够引入作为电机的加减速曲线。
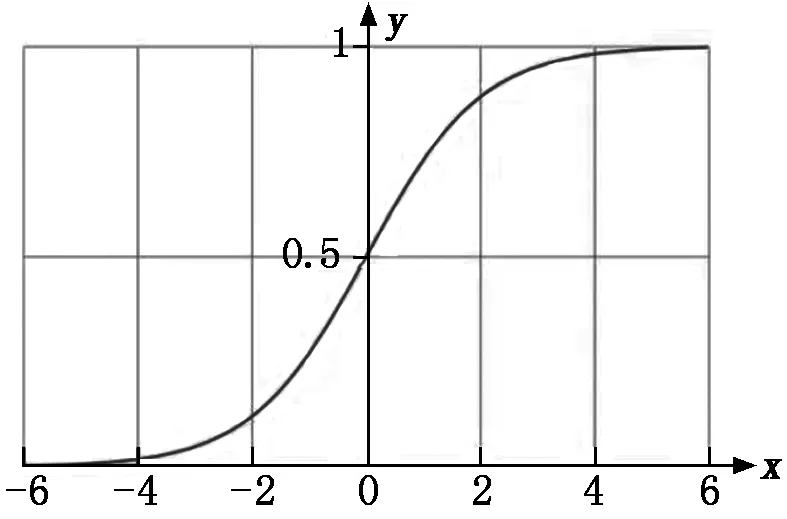
图3 Sigmoid函数曲线
由图3曲线可见,式(1)的曲线方程在x轴上有负值,因此不能直接用于步进电机的加减速控制,对方程(1)进行拉伸和平移,以适应电机加减速曲线的实际需要,变换后方程如下:
(2)
其中:A、B分别为y方向平移和拉伸分量;a、b分别为x方向平移和拉伸分量。
对比式(2)与式(1),y方向进行A分量的平移和B分量的拉伸,A、B分量可用于控制电机速度或频率的取值范围;x轴方向进行a分量平移与b分量拉伸,a分量与b分量用于控制电机速度或频率变化率。变换后的曲线依然是理论上的曲线,需要对曲线进行离散化使其能够适用于电机的加减速控制。离散即把曲线离散成各个频率段,在程序中保存时间点和与其对应的频率,并形成表格,在系统运行时根据已有表格中的频率值依次进行加载生成实际的脉冲曲线,使脉冲曲线与理论曲线相拟合,加速阶段的曲线离散后如图4所示。图4中,t1为中间速度(拐点速度)时刻,即电机在此时间前为加加速阶段,在此之后为减加速阶段;t2为电机加速完成进入均速运行时刻;t′为离散实现过程中将加速时间平均分成若干个固定长度的时间段。由于频率与速度之间只相差一个脉冲当量并且成正比关系,因此曲线算法也适用于速度。
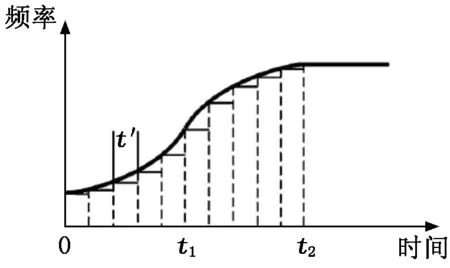
图4 加速阶段的曲线离散
离散化后,加速过程曲线方程为:
F=Fmin+(Fmax-Fmin)/(1+e-f(i-m)/m).
(3)
其中:F为加速曲线当前频率;Fmin为加速曲线起始频率;Fmax为加速曲线目标频率;i为循环计算索引,从0开始到选取的加减速点总数;f为曲线的斜率,f越大曲线越陡峭;m为1/2加减速点总数。
对应式(2),离散后相当于A分量=Fmin,B分量=Fmax-Fmin,a分量=f/m,b分量=f。
变量f取值的大小决定着S曲线压缩的程度,理想的S曲线f取值为4~6。设电机起始速度=20 r/min,电机最大速度=200 r/min,设f=4、f=5、f=6,求得三个f对应的速度曲线,如图5所示。

图5 三个f对应的速度曲线
从图5可以看出,在三个曲线中,遵循f越大曲线相对越陡峭,f越小曲线相对平稳,越接近匀加速的轨迹。由此可知,控制f的取值可以使得步进电机加减速时速度平滑地过渡。S型加减速算法原理设计曲线核心代码如下:
void CalculateSModelAccelLine(u16 usArrPerd[], float usLinePoint,float fMaxFreq,float fMinFreq,float fAccelRatio)
{
int i;
float freqTmp;
float deno;
float melo;
float delt=fMaxFreq-fMinFreq;
for(i=0;i { melo=fAccelRatio*(i-usLinePoint/2)/(usLinePoint/2);deno=1.0/(1+expf(-melo)); freqTmp=delt*deno+fMinFreq; usArrPerd[i]=(u16)(1000000.0/freqTmp); } } 应用STM32F103VCT6单片机来控制步进电机,以STM32F103VCT6的高级定时器产生PWM信号驱动电机,步进电机所需的驱动芯片选用东芝公司的TB6560,并将驱动电路设计到控制器内部。控制系统以定时中断加PWM的方式发送指定脉冲数,控制PWM输出引脚的电平即可控制脉冲数。PWM的输出由定时中断捕捉,一个脉冲需经两次定时器中断才能产生,由此可得到ARR(定时器装载值),计算方法如下: (4) 其中:fclk为定时器的时钟频率;fTarget为脉冲目标频率。 设定步进电机起始频率Fmin为1 000 Hz,最大频率Fmax为10 000 Hz,加加速度c为100 000脉冲/S3,采用Keil软件通过调试微控制器读取内存值,由内存值绘制频率与时间关系曲线,如图6所示。由图6可见,频率与时间关系曲线符合S型加减速特性,在加减速过程中能够平滑过渡。 图6 频率与时间关系曲线 在实际应用中对步进电机的控制一般有停机、加速、运行和减速4种状态,这4种状态对应了S型加减速曲线的整个过程,步进电机控制状态机如图7所示。 图7 步进电机控制状态机 根据电机控制的4个状态设计出控制代码,步进电机状态机核心代码如下: void MotorControl(void) { switch (g_stStepMotor.m_ucMotorState) { case MOTOR_STOP://停机状态处理 break; case MOTOR_ACCEL://加速状态处理 if (usAccelPulseNum { //加速点数未到,继续设定PWM频率 TIM3->ARR=(ucSpeedAccel[usAccelPulseNum]>>1); usAccelPulseNum++;// } if(usAccelPulseNum>=ACCEL_POINT_NUM) { //达到设定的加速点数,将电机状态切换至运行状态 TIM3->ARR=(ucSpeedAccel[ACCEL_POINT_NUM-1]>>1); g_stStepMotor.m_ucMotorState=MOTOR_RUN; } break; case MOTOR_RUN://运行状态处理 break; case MOTOR_DECEL://减速状态处理 if (usDecelPulseNum>0) { //减速点数未到,继续设定PWM频率 TIM3->ARR=(ucSpeedDecel[usDecelPulseNum]>>1); usDecelPulseNum--; } if (usDecelPulseNum<=0) { //达到设定的减速点数,停机处理 usDecelPulseNum=0; usAccelPulseNum=0;//清零相关数据 MOTOR_SET_TQ2; MOTOR_SET_TQ1;//释放电机力矩 MOTOR_DISABLE;//步进电机脱机控制 TIM_Cmd(TIM3,DISABLE);//失能PWM定时器 g_stStepMotor.m_ucMotorState=MOTOR_STOP;//切换至停机 } break; } } 研究了将S曲线引入步进电机的加减速控制中,通过对S曲线进行转换与离散,得出了可运用于实际电机加减速控制的方程,针对离散后的方程给出了S型加减速核心代码,并进行了仿真实验。仿真实验结果表明:步进电机按照改善后的S型曲线法进行加减速,整个运行过程较为平稳,没有产生冲击和跳变。3 单片机控制步进电机速度实验
3.1 脉冲频率输出
3.2 实验仿真

3.3 步进电机控制状态机

4 结语

