基于脉冲式力源的发动机试车台矢量推力校准装置设计及仿真
黄相华 杨海生 江 峰 杨水旺 宋志强
(1.北京振兴计量测试研究所,北京 100074;2.火箭军装备部驻北京地区第六军事代表室,北京 100070)
1 引 言
在发动机研制生产环节中,推力测试是评估发动机性能极为重要的参数之一。矢量推力测量数据的准确性直接关系到矢量发动机的性能,从而很大程度上影响着后续矢量发动机的研制、验证试验、飞行试验等[1]。
随着发动机矢量推力测量日益受到重视,发动机矢量推力校准也逐渐成为困扰发动机设计部门与试验部门的一个难题。目前,已经建设完成的试车台,推力校准基本还是采用实验室送检的方式进行。即把发动机试车台上的力传感器拆下后,送到有资质的实验室进行校准,再装回到发动机试车台上进行试验测试。
传统推力校准方法存在以下几个问题。
1)测力传感器的校准是在理想静态环境下进行的,得到灵敏度系数,但是在实际测试环境中测量的是动态力值信号,测量数据误差较大;
2)矢量推力测量系统的各个测量仪器只能单独进行校准,不能做到系统校准,对于整个测量系统的测量不确定度无法有效评估;
3)目前在用的发动机试车台,仅局限于对推力进行单分量校准,通过计算公式将各个方向的推力合成,得到矢量推力的校准结果,与发动机实际工作状况存在较大差异。
通过分析可知,传统的校准方式已经不适应飞速发展的矢量推力试验技术[2-7]。本文提出一种基于脉冲式力源的发动机试车台校准装置,对试车台进行矢量推力校准。设计完成后对校准方案进行了动力学建模及仿真,对测量结果进行了测量不确定度评估。
2 矢量推力现场动态校准方案
2.1 矢量推力校准技术方案的确定
发动机试车台上矢量推力测量系统在试验时,可以分别测得主推力Fx和侧向力Fy,Fz,矢量推力的幅值大小即可由空间正交力的形式表示。当矢量推力测量系统测得空间正交力Fx,Fy,Fz的幅值大小后,可通过式(1)计算,从而得到矢量推力F为
(1)
而发动机试车台矢量推力的另外一个参数,偏斜角α可以通过式(2)计算得出
(2)
由此可以看出,把主推力和侧向力各个方向的传感器都进行动态校准后,就可保证通过公式计算矢量推力大小和偏斜角大小的准确度。本项目的研究重点是动态校准装置设计,设计原理总体框图如图1所示,并通过数采系统分别得到矢量推力校准装置和试车台矢量力测量系统的力值曲线,通过比较法实现力传感器动态校准,进而保证矢量推力测量系统测量结果的准确性。
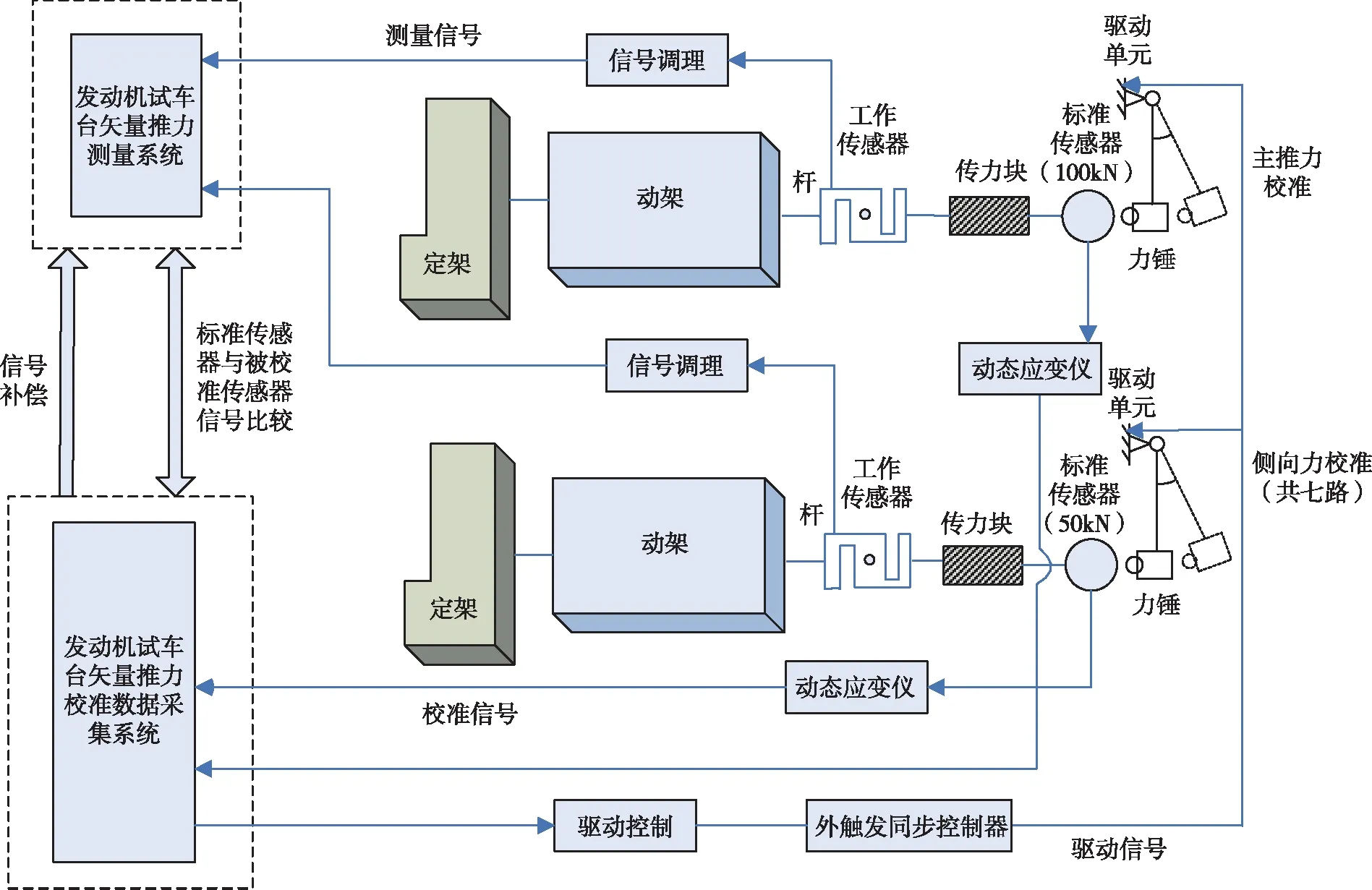
图1 发动机试车台矢量推力校准总体框图
通过调研,对现阶段已经得到应用的矢量力发生装置的优点及缺点进行比较[8-12],确定了采用摆锤式动态力发生装置作为现场矢量推力校准的动态激励源,以完成发动机试车台矢量推力的校准工作。
整套校准装置根据施加作用力的方向与力值的大小,可以分为主推力校准模块与侧向力校准模块。在进行校准时,根据需要提供的激励波形,调整校准摆锤激励系统的工作参数,如摆锤的提升高度、摆动角度、摆锤的锤头质量等,可以获得不同幅值与脉宽组合的半正弦冲击力信号。
随后将校准装置所采集到的标准动态力信号,与矢量推力测量系统采集到的测试数据进行比较。通过数据融合、矢量推力动态特性的获取、测量系统幅频相频特性的补偿等数据处理方法,实现发动机试车台矢量推力的现场校准。
2.2 摆锤式脉冲激励装置的设计
发动机试车台矢量推力现场动态校准是通过矢量推力校准装置和试车台矢量力测量系统之间比对来实现,而摆锤式动态力发生装置用于提供一个便于测量和分析的半正弦力值信号。摆锤式的矢量推力激励装置机械结构如图2所示。
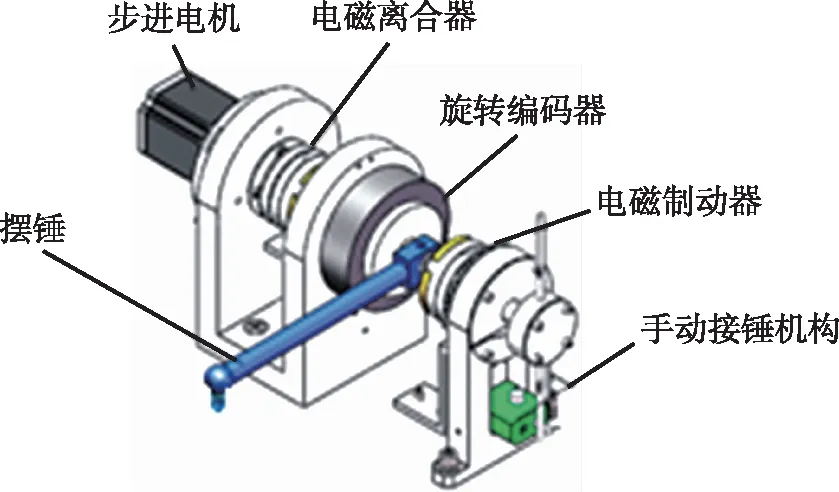
图2 激励装置机械结构图
为了能够快速便捷产生一定幅值和脉宽半正弦力值信号,需要对摆锤工作状态参数(锤头质量、摆臂长度、摆动角度、材料刚度等)与其所产生动态力之间数学关系进行进一步理论分析和仿真研究。为确保摆锤动态力幅值准确度和稳定度,需对摆锤摆动角度精确定位。通过相应机电元件测出摆锤摆动角度,并反馈至控制单元,通过驱动电机精确控制摆锤摆动高度。
2.3 传力块的设计
为产生便于分析与测量的半正弦激励信号,摆锤式矢量力发生装置通过撞击传力块,得到不同脉宽、不同幅值的冲击力值信号。
传力块与摆锤锤头以及工作级传感器连接方式如图3所示,图中传力块采用40Cr或炮钢材料,其上放置可换材料,产生校准所需脉宽。
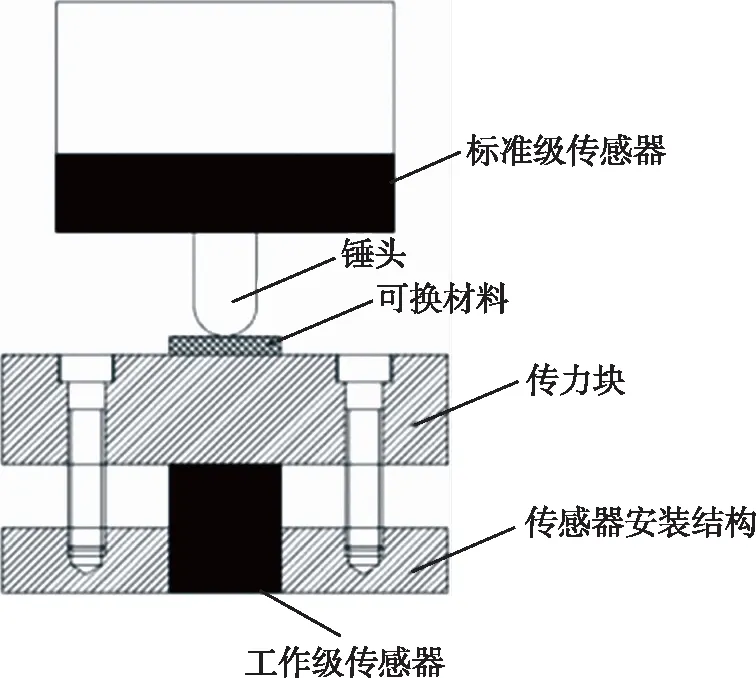
图3 传力块结构图
假定可换材料为规则形状,受力面积为A,厚度为T的条件下,线性恢复力系数k有关系式为
(3)
式中:E0——可换材料的初始弹性模量。
根据式(10),可换材料可设计成圆柱体或长方体型等规则形状,若保证可换材料受力面积和厚度之比A/T为0.1,则系数k近似等于E0/10,根据仿真结果,可换材料初始弹性模量E0应控制在(0.5~10)GPa范围内,因此可选择聚乙烯(0.49~2.50)GPa、尼龙(1.07~2.83)GPa、酚醛塑料(3.92~8.83)GPa和铅17GPa等不同初始弹性模量材料作为可换材料使用。
为了使得撞击力能够尽可能沿着垂直于工作级传感器敏感面方向进行传递,当摆锤式动态力发生装置锤头与可换材料接触时,锤头与传感器敏感面近似保持垂直状态。此外还需调节好摆锤锤头与传力块对中精度,从而进一步保证传力方向与工作级传感器垂直度在误差允许范围之内。
3 脉冲式力源的力学仿真分析
3.1 模型的建立
根据前文的分析可知,通过合理调整系统参数,如摆锤质量、提升角度、可换材料等即可获得不同脉宽及幅值力值信号[13]。摆锤式动态力发生装置的力学模型如图4所示。
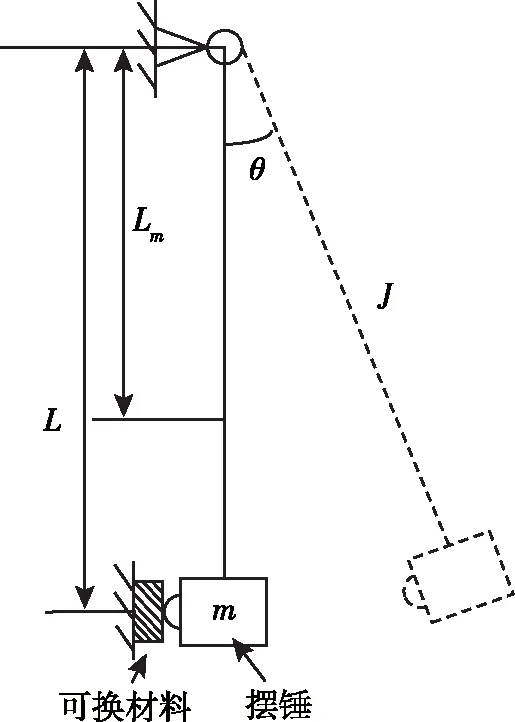
图4 摆锤式激励装置力学模型图
将摆锤激励系统进行简化,摆锤视为理想刚体,其几何尺寸不随冲击力值的变化而变化。取摆锤为研究对象,摆锤撞击可换材料的初始角速度ω由摆锤的提升角度θ来决定。
当摆锤激励系统中的摆锤从初始位置到达击打位置时,摆锤所能达到的势能为
Ep=mgLm(1-cosθ)
(4)
式中:Lm——摆锤摆杆系统质心到转动中心的长度;m——摆锤质量;θ——摆锤提升角度。
当摆锤激励系统的摆锤到达击打位置时,其动能可以用式(5)表示
(5)
式中:J——摆锤相对于转动中心点的转动惯量。
将摆锤系统视为理想状态时,根据能量守恒定律,可以认为摆锤激励系统Ep=Ek。
由此可以得到摆锤在撞击传力块前的冲击速度为
(6)
式中:L——转动中心与摆锤击打点之间的距离。
考虑到在设计时摆锤激励装置中摆锤质量远大于摆杆,摆锤自身尺寸相对较小,和摆杆相比可忽略,因此摆锤质心到转动中心距离Lm和转动中心到摆锤冲击点距离L近似相等,摆锤对摆动中心转动惯量J≈mL2,则有
(7)
以摆锤旋转至与可换材料碰撞瞬间为时间零点,可换材料与摆锤的接触点为坐标原点,根据牛顿第一定律,可以得到摆锤激励系统的力学方程为
(8)

一般在工程应用中,可更换材料一般可以分为双曲正切型非线性材料、正切型非线性材料、三次型非线性材料等几个种类。在本项目中,采用的是三次型非线性材料,故而,摆锤的弹性恢复力可以用式(9)表示
F(x)=kx+δx3
(9)
式中:k——线性恢复系数;δ——非线性恢复系数。
将式(9)代入式(8),变换后,可以得到摆锤激励系统的摆锤力学方程为
(10)

(11)
采用数值计算法,利用Matlab对上述二元一阶常微分方程组进行求解,可以得到所需的计算结果。
为详细分析摆锤冲击过程中的变量对冲击力幅值和冲击力脉宽等数值的影响,在设计之初可以分别以可换材料的k,δ,θ,m,L等为变量,对设计方案进行仿真,并分析各种变量对最终产生的半正弦冲击力所产生的影响。
3.2 冲击过程的半正弦力值时域与频域仿真
为了便于分析,设摆锤装置打击传力块产生的力脉冲信号为理想半正弦,则力脉冲信号可表示为
(12)
式中:Fm——脉冲力峰值;τ——脉冲力脉宽。
选取半正弦力脉冲信号幅度谱密度由1下降至0.1的频率段作为信号的有效频带,分别对脉宽为0.1ms,0.5ms和1ms的归一化理想半正弦力脉冲信号进行分析,得到的频谱仿真图如图5和图6所示。
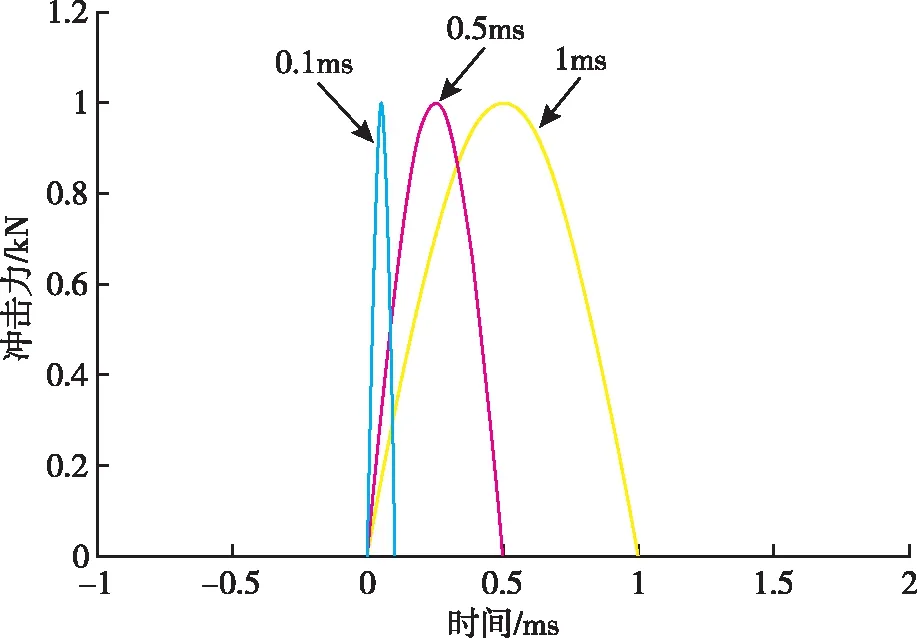
图5 冲击过程的半正弦力值时域仿真图
从图5和图6可知,脉宽为0.1ms,0.5ms和1ms的归一化理想半正弦力脉冲信号的有效频带范围分别为13 120Hz,2 607Hz和1 303Hz,为了达到技术指标,力脉冲信号的脉宽应控制在1.3ms以内。
3.3 激励系统的冲击力仿真结果
下面针对各种参量作为设计变量,分别加以仿真,以验证所设计摆锤激励系统的结果[14]。
3.3.1不同k值条件下冲击力仿真
根据设计输入条件,确定初始条件:摆锤激励系统的初始摆角θ=90°,材料的非线性恢复系数δ=1×1010,摆锤的质量m=5kg,转动中心到摆锤冲击点的距离L=1m,在线性恢复力系数k=[5×107,l×l08,2×108,5×108]的不同条件下,利用Matlab进行数值仿真,得到在不同k值下的摆锤激励系统冲击力值曲线,如图7所示。
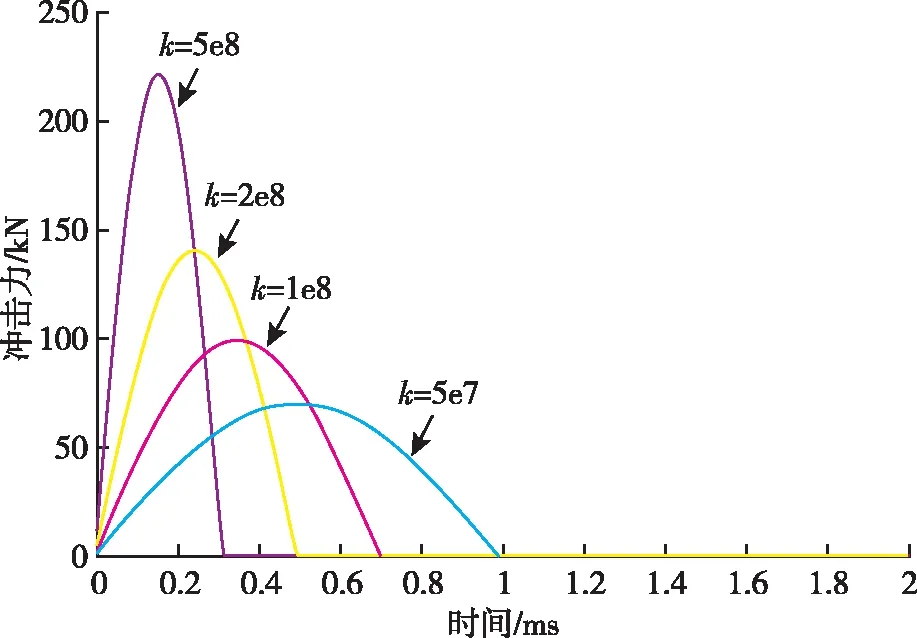
图7 不同k值条件下冲击力仿真图
从图7中的仿真结果可以看出,激励源在冲击过程中产生的为半正弦式脉冲力波形,其脉冲力幅值与可更换材料的k值大小成正比,而脉冲力的脉宽与可更换材料的k值大小成反比。材料的线性恢复力系数k对脉冲力的幅值和脉宽的影响均较大。
3.3.2不同δ值条件下冲击力仿真
选取仿真初始条件:[k,θ,m,L]=[5×106,90°,10,1],分别取δ=[0,l×1010,5×1010,1×1011],仿真得到的不同δ值下的摆锤激励系统冲击力值曲线,如图8所示。
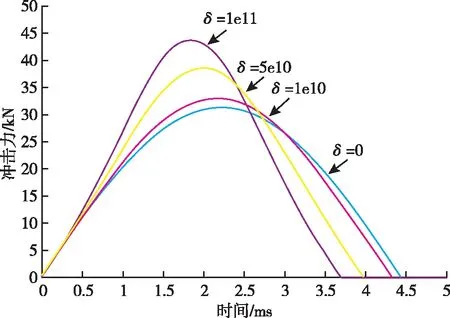
图8 当k=5×106时不同δ值下冲击力仿真图
选取仿真初始条件:[k,θ,m,L]=[1×107,90°,5,1],分别取δ=[0,1×109,1×1010,1×1011],仿真得到的不同δ值下的摆锤激励系统冲击力值曲线,如图9所示。
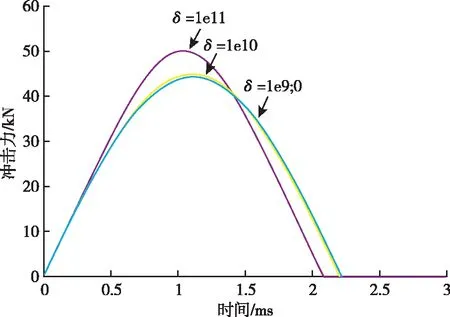
图9 当k=1×107时不同δ值下冲击力仿真图
选取仿真初始条件:[k,θ,m,L]=[1×108,90°,5,1],分别取δ=[0,1×109,1×1010,1×1011],仿真得到的不同δ值下的摆锤激励系统冲击力值曲线,如图10所示。
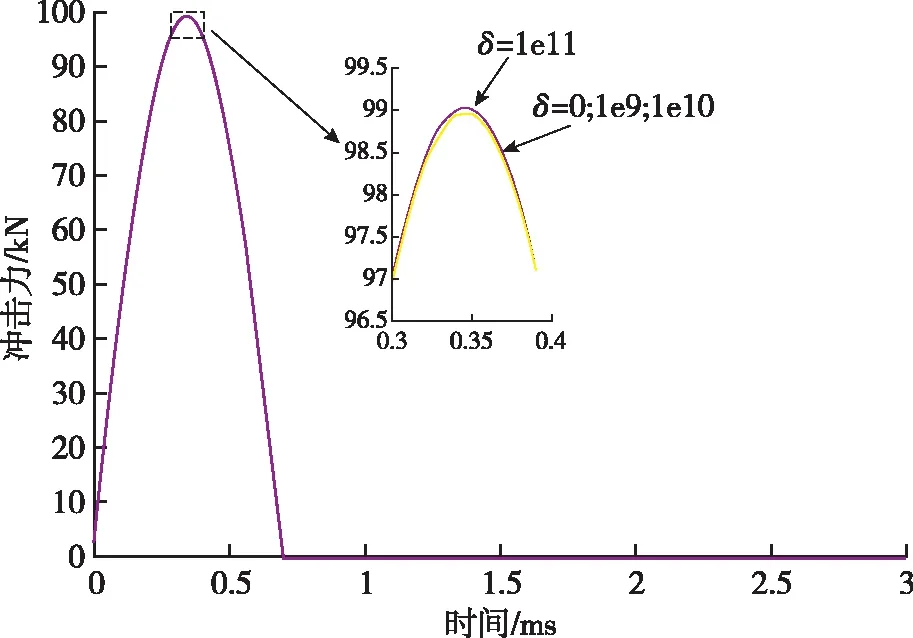
图10 当k=1×108时不同δ值下冲击力仿真图
从仿真结果可以看出,摆锤冲击过程中随着δ的增加,冲击力峰值增大,而脉宽则随之减小。
这说明在设定了相同的试验参数时,当可换材料的非线性恢复系数越大时,摆锤激励系统所产生的动态力幅值就越大,冲击力脉宽越窄;反之,当可换材料的非线性恢复系数越小时,摆锤激励系统所产生的动态力幅值就越小,冲击力脉宽也越宽。
3.3.3不同θ值条件下冲击力仿真
选取仿真初始条件:[k,δ,m,L]=[1×108,1×1010,5,1],分别取θ=[30°,60°,90°,120°],得到在不同摆角条件下摆锤激励系统冲击力值曲线,如图11所示。
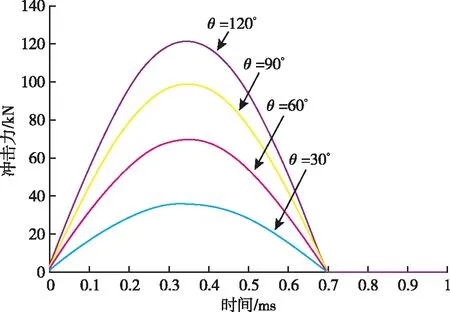
图11 不同θ值条件下冲击力仿真图
从仿真得到的结果可以看到,激励系统的θ值越大,脉冲力的幅值越大,而脉冲力的脉宽在改变θ值的过程中变化不大。
3.3.4不同m值条件下冲击力仿真
选取仿真初始条件:[k,θ,δ,L]=[1×108,90°,1×1010,1],分别取m=[1,5,10,15],得到在摆锤质量不同的条件下摆锤激励系统冲击力值曲线,如图12所示。
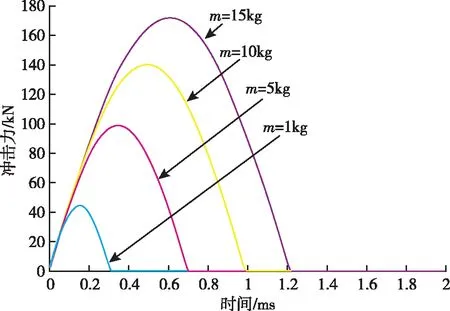
图12 不同m值条件下冲击力仿真图
由图中的仿真结果可以看到,随着锤头质量m的增大,激励系统的脉冲力幅值与脉宽均会增大,且脉冲力幅值增大的幅度更明显。
3.3.5不同L值条件下冲击力仿真
选取仿真初始条件:[k,θ,δ,m]=[1×108,90°,1×1010,5],分别取L=[0.5,1,1.5,2],得到在L值不同的条件下摆锤激励系统冲击力值曲线,如图13所示。

图13 不同L值条件下冲击力仿真图
摆锤冲击过程中的力峰值随着L的增加而增大,而力脉宽则随着L的增加而减小。转动中心到摆锤冲击点的距离L对力信号峰值影响较大,对脉宽影响较小。
从分析可知通过合理的调整系统参数即可获得不同脉宽及幅值的力值信号。根据上文中的仿真结果,本项目主要通过改变摆锤质量m、摆杆长度L、摆动角度θ和可换材料线性恢复力系数k这四个参数来控制力脉冲信号的峰值和脉宽。其中,摆锤质量可通过设计多组不同质量(0.1kg,0.2kg,0.5kg,1kg,2kg和5kg)的组合式配重片来进行调节;摆杆长度可通过设计多组不同长度(0.1m,0.5m和1m)的摆动杆来进行调节;摆动角度在0°~120°范围内可调。
4 试车台矢量推力测量不确定度分析
依据现场的校准过程,提炼出发动机试车台矢量推力测量不确定度分量,进行分析,并加以汇总,进行测量不确定度的合成[15]。测量不确定度分量评估表见表1。
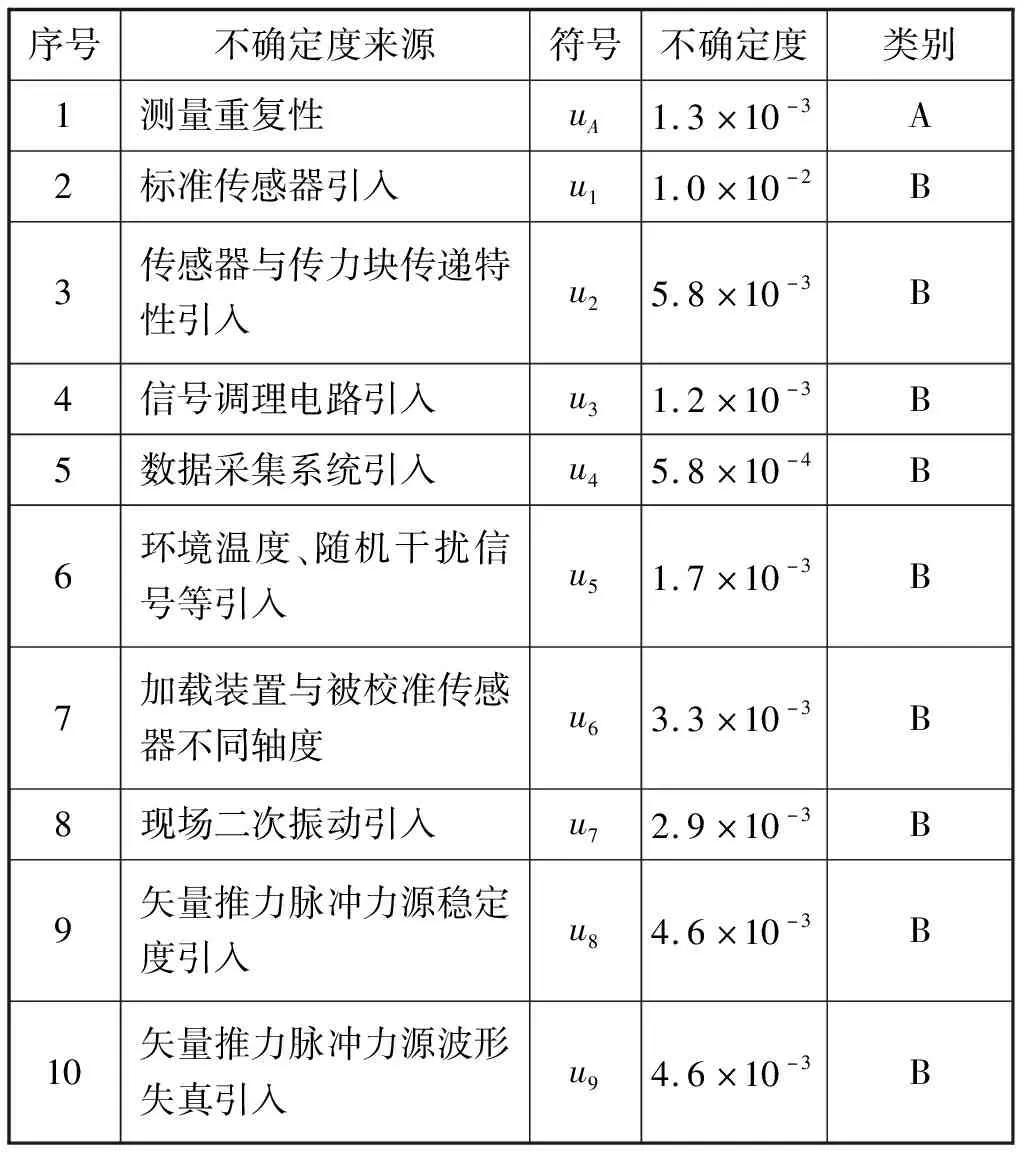
表1 试车台矢量推力测量不确定度评估表
测量不确定度合成为
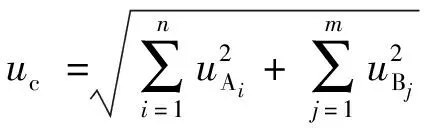
=1.5%
试车台矢量推力校准扩展不确定度为
Urel=kuc=2×1.5%=3.0%(k=2)
5 结束语
针对发动机试车台矢量推力现场校准需求,重点研究了基于脉冲式力源的试车台矢量推力校准装置总体方案、脉冲力源及传力块的设计、脉冲力源的力学仿真分析、试车台矢量推力测量不确定度评定等工作,建立了发动机试车台矢量推力校准装置,解决了发动机试车台现场校准的难题。该校准技术的研究成果能够填补国防军工行业在发动机试车台矢量推力现场校准领域的空白,对于科研生产有着重要的理论和应用价值。另外通过简单的结构改造后,该项校准技术也可应用于其他行业的发动机试车台测试校准工作,应用前景广阔。

