日月影响的地球重力加速度精确计算方法

黄劲松 傅 瑜

(中国运载火箭技术研究院，北京 100076)

1 引 言

地球表面上重力加速度

g

与一些因素的集合有关，这些因素包括所研究点的地理位置和高度、地球、太阳和月球的重力、地球围绕自身轴和沿绕太阳轨道的转动、地球轴相对黄道面的倾角、一年和一昼夜的时间等，即它是对不同位置和时间取不同值的变量。准确地求出以m/s、cm/s、伽(1伽=1cm/s)、毫伽(1毫伽=0.001cm/s)计量的自由落体绝对加速度，对宇航学、导航、大地测量、估计全局地球物理气象过程以及军事应用等都具有非常重要的意义。

2 问题的提出

使用各种摆式仪表和重力测量仪、弹簧式和弦式测力计、杠杆式称重等设备直接测量重力加速度是非常困难的，这需要详细完成大量的工作，并且通常情况下这类仪表的可靠性需要标好刻度来实现，这就导致在必须可靠地确定地球表面上任意一点的重力加速度时存在一定的困难。因此，为了得到在整个地球上的基准重力网，波茨坦城重力加速度的绝对值曾被取为基准单位，由Kuhnen.F、FurtwanglerPh(1898～1904)用五个回转摆在40次系列试验中以直接测量的方式，确定了

g

=981274±3毫伽的形式。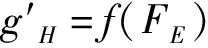

研究人员对重力加速度标准部分

γ

值的计算进行较多研究，他们在理论探索和在波茨坦坐标系进行大量实际测量试验结果分析的基础上，提出了一系列在精确球体条件(

H

=0)下确定

γ

值的解析关系式。1930年于斯德哥尔摩市举行的大地测量会议上认定下面的Cassinis公式为国际公式(

γ

值的计量单位是毫伽)

γ

=978049

.

0·(1+0

.

0052884sin

φ

-0

.

0000059·sin2

φ

)

(1)

但之后在详细完成不同地理点的多次重力测量与卫星观测数据分析的基础上确认，波茨坦系把加速度值提高了大约14毫伽。因此在1971年于莫斯科市举行的国际大地与地球物理测量会议上曾确立了新的确定标准的重力加速度公式，该公式考虑了观测点在海平面以上高度

H

的影响，其表达形式如下：

γ

=978031

.

85·(1+0

.

005302·sin

φ

-0

.

0000059·sin2

φ

)-0

.

3086·

H

(2)

公式(2)给出了考虑物体纬度和高度位置时重力加速度的标准值(近似值)，为了更精确地确定绝对值

g

，必须附加地考虑由各种因素作用造成的异常值(简化)，为此本文介绍一种考虑太阳和月球影响的方法重力加速度值计算方法。

3 方法构建与求解

来自月球引力的加速度

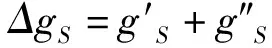
Δg

与所研究时刻月球在轨道上的位置有关，特别是该轨道被地球-月球地心轴与地球表面交点的坐标(

φ

,

λ

)确定。于是，考虑上述因素的重力加速度

g

的广义量由公式(3)确定：

g

=

γ

+

Δg

+

Δg

(3)

式中：

γ

——考虑到所研究点的纬度和高度位置，按公式(2)确定的自由落体标准加速度；

Δg

,

Δg

——分别为由太阳和月球引力以及地球围绕太阳运动形成的引力加速度值的异常。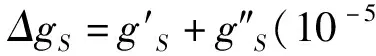

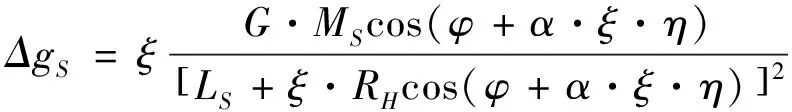
(4)

式中：

M

——太阳的质量1

.

989·10

kg

；

G

——重力常数6

.

6720·10

Nm

/

(

kg

·

s

)；

α

——地球轴相对黄道平面的倾角23

.

5°；-90°≤

φ

≤90°——所研究点的地理纬度。它与地心纬度之间的差别很小(<0

.

1°)，对北半球、南半球和赤道的取值范围分别是

φ

>0,

φ

<0,

φ

=0；

R

——从所研究的海平面上高度

H

处的点到地球中心的距离，按公式(5)计算

R

=

R

+

H

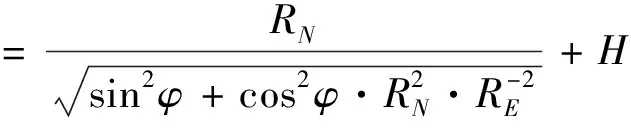
(5)

式中：

R

——球形地球的矢径；

R

——地球的赤道半径,

R

——地球的极半径，其值分别为

R

=6378.164·10m，

R

=(1-

ε

)

R

=6356.799·10m；

ε

——地球扁率，0

.

00335；按公式(6)计算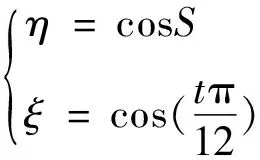

(6)

式中：

η

——考虑一年时间的系数；

ξ

——考虑一昼夜时间的系数，

S

——数值上等于天数的以度为单位的角度：对于第一个半年从所考虑的日期到6月22日，而对于第2个半年从6月22日到所考虑的日期(太阳系半年)；

t

——当地一昼夜时间内的一个数(以小时记)；按公式(7)计算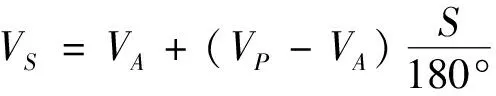

(7)

式中：

V

——地球在黄道平面内沿黄道轨道运动的线速度当前值，

V

——地球绕太阳轨道运动在远日点的线速度，29.27×10(m/s)，

V

——地球绕太阳轨道运动在近日点的线速度，30.27×10(m/s)。按公式(8)计算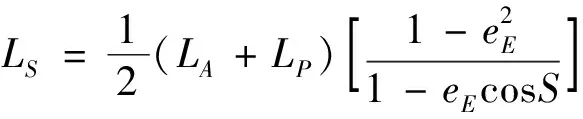

(8)

式中：

L

——所研究的日期从地球到太阳的日心距，

L

,

L

分别表示在远日点(6月22日)和近日点(12月22日)上从地球到太阳的距离

L

=152098.233·10m，

L

=147098.291·10m，

e

——地球轨道的偏心距，0.0167112。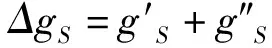

对于给定的时间，根据月球的位置和地球-月球地心轴的坐标(

φ

,

λ

)，按公式(9)计算月球重力

F

对重力加速度的影响

Δg

=

f

(

F

)(10毫伽)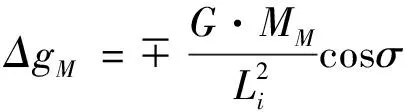

(9)

对地球朝向月球方向该公式取负值“-”，而对地球的背对月球方向取正值“+”。

式中：

M

=7.35·10kg为月球的质量；

L

——从月球到所研究的地球表面上坐标为(

φ

,

λ

)的点的距离，其中-180°≤

λ

≤180°为所研究点的地理经度(

λ

>0,

λ

<0,

λ

=0相应地对应于东经、西经和零子午线)，按公式(10)计算

L

=

L

-

R

·cos

σ

(10)

式中：

L

——地球到月球的当前距离，对于月球的椭圆轨道按公式(11)计算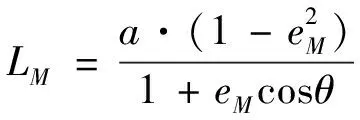

(11)

式中：

e

——月球绕地球轨道的偏心率，0

.

055；

a

=384.40·10m，月球轨道的长半轴(沿拱点线)；

θ

表示月球轨道平面内地球-月球地心轴相对拱点线(相对近地点)的偏角(顶点在地球中心)，根据计算日期月球的位置求出；

σ

——顶点在地球中心的地球-月球地心轴坐标(

φ

,

λ

)和所研究点(

φ

,

λ

)的地理位置之间的夹角，按公式(12)计算

(12)

式中：

Δφ

=|

φ

-

φ

|；

Δλ

=|

λ

-

λ

|，当

Δλ

>180°时应该按照

Δλ

=360°-|

λ

-

λ

|计算。角

σ

的变化范围是：对于地球朝向月球的那一面0≤

σ

≤90°；对于地球背对月球的那一面90°≤

σ

≤180°。根据专门计算所研究日期上月球在绕地球轨道上的位置计算出点(

φ

,

λ

)的坐标值和角度

θ

，在这种情况下纬度坐标的变换范围-18

.

36°≤

φ

≤18

.

36°，当月球沿拱点线位于轨道上时，近地点和远地点上达到极值(最小和最大值)。零值

φ

=0对应于月球处于节线上(在升交点和降交点附近)，这时

θ

=90°。

4 结果分析与示例

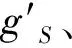
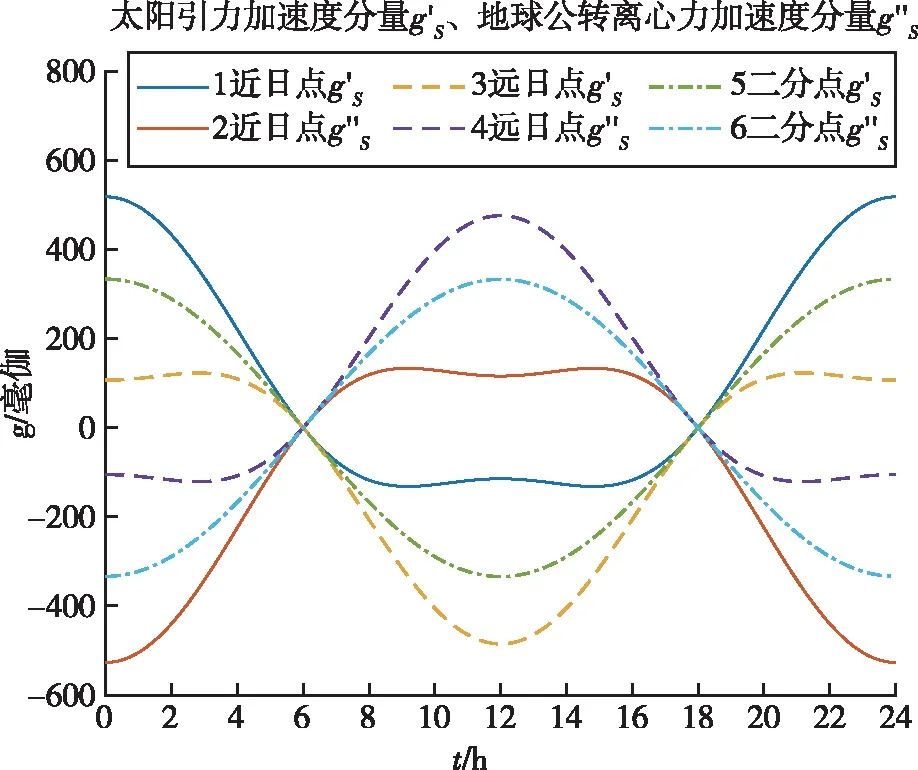
图1 太阳引力及离心力相关加速度

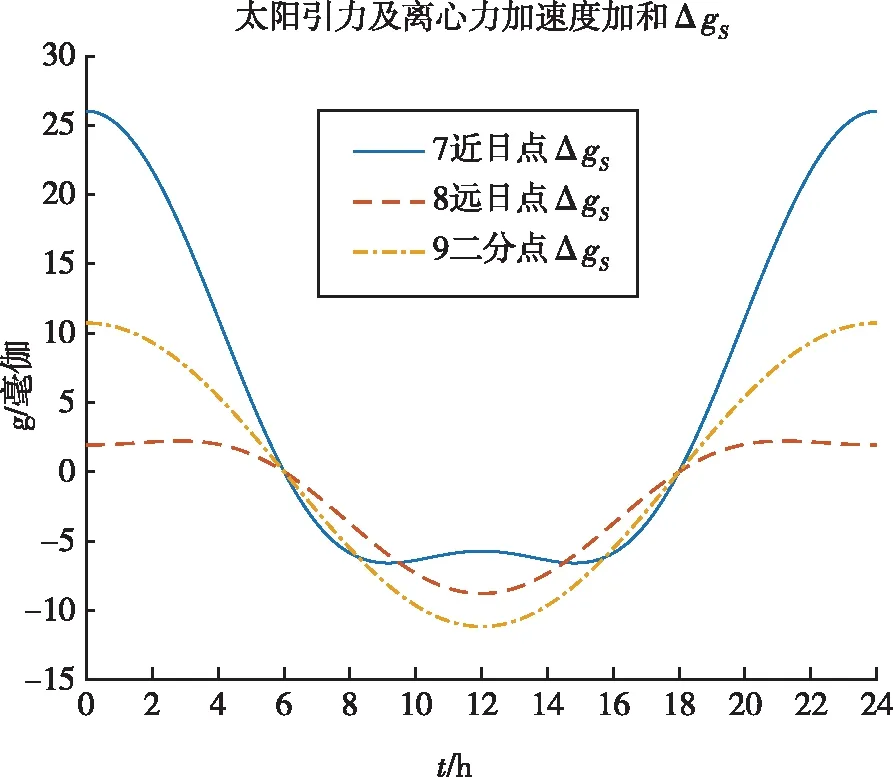
图2 太阳引力及离心力相关加速度和ΔgS

在早晨和晚上(

t

=6,18)，因为作用力朝向地球表面的切线方向，所以太阳对重力加速度不产生影响。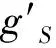

除此之外，对地球绕自身轴和沿绕太阳轨道运动的分析得出，对于躺卧状态的人体组织来说，最有利的状态是沿子午线躺卧。当身体转变到头朝西或者是头朝东时，夜间和早晨单方向的切向和切向-离心加速度使血液向头部或脚部流动。

对于近日点夜间与白天(

t

=0;12,

S

=180°)地球上不同点处考虑高度

H

的按公式(2)计算出的最大的标准加速度

γ

和按公式(3)～(5)计算出的广义加速度

g

值的比较结果在表1中给出，括号中给出标准加速度

γ

和广义加速度

g

值之间的差值。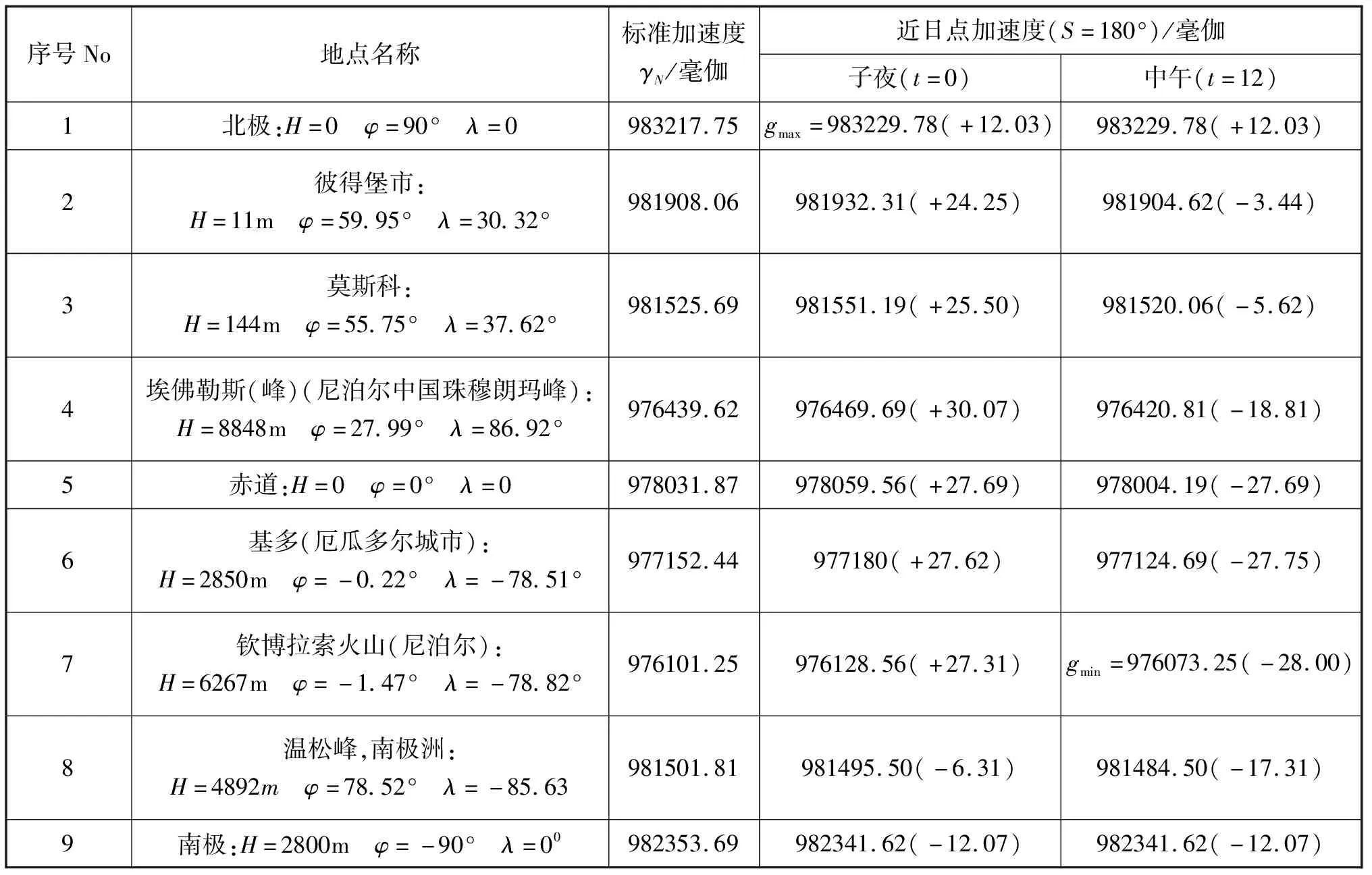

表1 近日点时各地昼夜的加速度

从表1中可以看出，与一年中和一昼夜内的时间有关，广义加速度

g

取与标准加速度

γ

不一样的变化的值，相应地达到30.07和-28.00毫伽。在近日点(P)北极(

t

=0;12)加速度

g

达到最大值983229.81毫伽，在钦博拉索火山顶峰(

t

=12)达到最小值976073.25毫伽和最小值。在两极的加速度的大小有不同的值——北极的大，南极的小。对于地球上不同点，月球引力

F

对重力加速度的影响

Δg

=

f

(

F

)，在2019年12月26日(

S

=179°,

t

=12)新加坡市全日食期间(

H

=15

m

,

φ

=1

.

35°,

λ

=103

.

85°)，在地球-月球地心线与节点线上地球表面的交点处，即

θ

=90°广义加速度

g

的计算结果在表2中给出。从表2中可以看出，月球引力

F

对重力加速度的影响取变符号的值——在地球朝向月球的这面取负值，在地球背对月球的面取正值。对于所研究的情况，加速度

Δg

=

f

(

F

)的最大值(绝对的)等于-3.29毫伽，在地球-月球地心线与节点线上地球表面的交点处。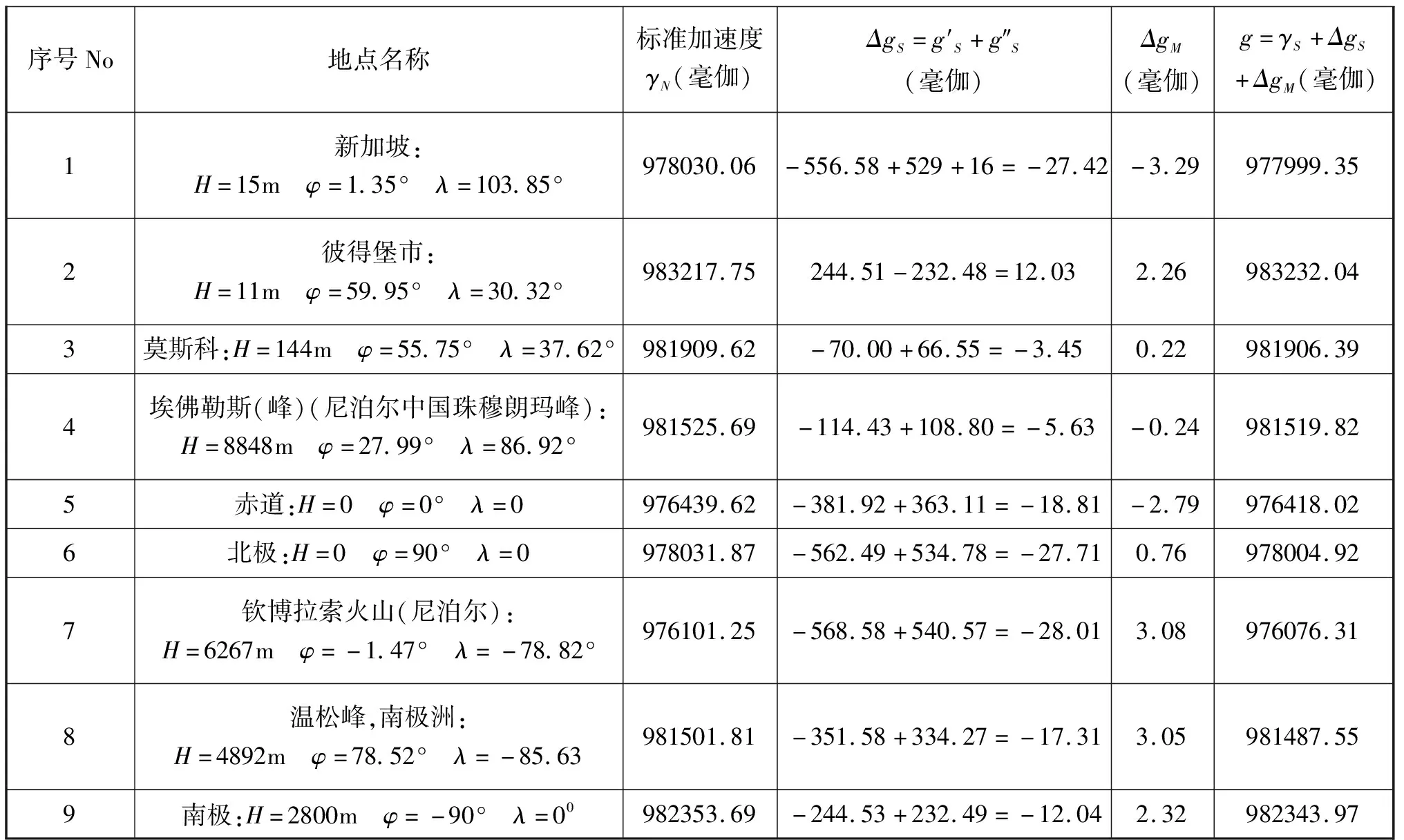

表2 新加坡全日食期间各地的加速度

4 结束语

在自由落体标准加速度国际公式的基础上，得到了与地球、太阳和月球引力、海平面以上的高度、一年和一昼夜间的时间有关的地球表面任意一点的广义加速度的计算公式，并得出在两极的加速度的大小有不同的值——北极大南极小。

地球在近日点时，加速度在北极(子夜、中午)和钦博拉索火山顶峰(子夜)处，分别达到最大值983229.81毫伽和最小值976073.25毫伽。在一昼夜期间由重力和离心力造成的变号加速度分量没有被完全“平衡”，例如，对钦博拉索火山在近日点子夜分别是-568.57毫伽和+540.56毫伽。

在近日点太阳对地球上重力加速度施加的影响最大，一昼夜间加速度波动幅值达55.34毫伽(对钦博拉索火山夜间加速度增加达27.34毫伽，而白天减少达-28.00)。在早晨和晚间太阳对加速度的影响不大，因为重力沿地球表面的切线方向。

来自月球引力的加速度对地球朝向月球的表面取负值而对背对月球的那一面取正值，并且其绝对值相对较小(达3～4毫伽)。

由太阳和月球影响带来的一昼夜和一年间加速度的不对称波动对地球运动的集成作用最终被地球绕自身轴旋转和沿轨道运动的特点所“吸收”。