原子频标中激光器高偏振态检测器件设计研究

陈妍君 黄 凯 王秀梅 王晓露 王 亮 高连山

(北京无线电计量测试研究所，北京 100039)

1 引 言

波片也称为相位延迟器，用于使两个互相垂直的线偏振光之间产生一定的相位延迟，从而改变入射光的偏振态。在需要对光束偏振态进行检测或调控的原子频标中，波片起到至关重要的作用。原子频标系统架构随着航天及对地标准的集成化与一体化需求日趋小型化。因此要求原子频标中光学模块的光学器件也趋于微小型化发展。由于传统波片通常由双折射晶体制成，其体积大、在设备小型化、集成化等方面遇到瓶颈，器件的性能也会受到材料特性的限制。因此需要设计体积小、厚度薄、可集程度高的亚波长偏振调控器件，通过对子单元的结构设计、空间排布，使得入射光与每个子单元产生强烈的光学响应，实现亚波长结构器件对光场相位、振幅、偏振态的调控。为此研究者们逐渐将焦点转向对亚波长纳米结构器件的研究上，与传统晶体材料波片相比，由二维周期阵列构成的超薄纳米器件有能力增强电磁场的强度并对光的偏振态进行调控，对于原子频标中光学模块的小型化与集成化发展具有重要意义。

2011年，Anders等学者利用有限元商业软件仿真，设计出金纳米十字结构和纳米砖型结构，分别在波长为1 520nm和770nm实现了反射波片的功能，可以将线偏振光转化为圆偏振光。2012年，Jean等学者利用银椭圆环形孔径阵列设计并制造出可见光波段的四分之一波片。2013年，Zhao等学者利用有限时域差分法商业软件FDTD仿真，设计出贴片式纳米天线，该结构实现了透射式波片的功能。2013年，Zhao等学者利用特定排布厚度为几十纳米的交叉银纳米天线，实现正交方向的相位延迟，实现特定的偏振态转换。2015-2016年，Wen等学者利用梯度排布的金纳米棒制作超表面，可以将入射光分解为左旋圆偏振光与右旋圆偏振光，进而可以测量原偏振光的椭偏度及手性。然而，先前的研究没有对波片的性能进行分析，并且也没有考虑实际应用中消色差波段及透过率，只是证明这些结构可以实现对光偏振态的调控功能。

我们利用时域有限差分法来求解空间电磁场的分布。将矩形纳米棒等效为两个正交的伴有电偶极矩的偶极子，在两个正交方向会引入相位差，当相位差满足π/2时可以产生圆偏光。本文中我们主要对波片的消色差波段及消色差波段的透过率进行研究。仿真结果表明，利用线偏振光垂直照射波片表面，当正交电矢量的相位差值误差控制在±2°时，消色差波段为620nm～668nm，与此同时该波片在消色差波段最低透过率高于40%，最高透过率为48%左右，这是可以与传统双折射晶体波片相比拟的。为光学模块的小型化、集成化奠定基础，有利于辅助激光器调制出高效的偏振光。

2 理论与仿真

在这一部分，

λ

/4波片结构图如图1所示。它由镀在基底为SiO上的银纳米棒阵列组成。方案中，银纳米棒之间的距离足够远来避免相互之间的耦合作用。矩形银纳米棒可以等效为两个正交的伴有电偶极矩的电偶极子，并且在远场的观察区域近似在

z

轴附近(

z

>>

x

,

y

)。

图1 波片原理图

两个独立的偶极子的极化率可以表示为

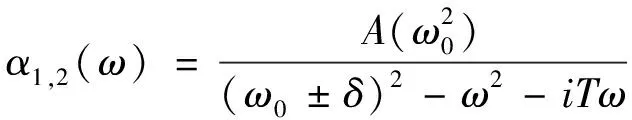
(1)

式中：

δ

——失谐频率；

A

——共振强度；

T

——阻尼系数；

ω

——中心频率。

我们选择相反地两个偶极子都略微失谐于中心频率。因此两个偶极子极化率之间的相位差为

ψ

(

ω

)-

ψ

(

ω

)=

π

-2

arctan

(

T/

2

δ

)

(2)

利用时域有限差分法进行透射场的数值仿真。这里优化出

λ

/4波片的参数为长

a

=250nm，宽

b

=120nm，厚度

t

=40nm，周期

p

=300nm，如图2所示。玻璃基底的折射率为1.5，并且假设玻璃基底无限大。

图2 波片子单元结构图

在

x

、

y

轴方向应用周期性边界条件，在

z

轴方向应用完美匹配层边界条件。矩形银纳米天线等效为两个正交偶极子，每个偶极子在与偏振方向垂直的两边激发表面等离子体共振。在波长为633nm时近场电场图样分布如图3所示。当入射电场方向沿

x

(或

y

)方向时，电场主要聚焦在与入射光偏振方向垂直行的两边(图3(a)和3(b))。当偏振方向为45时，电场存在于四边，模式图样是前面提及图样的叠加如图3(c)。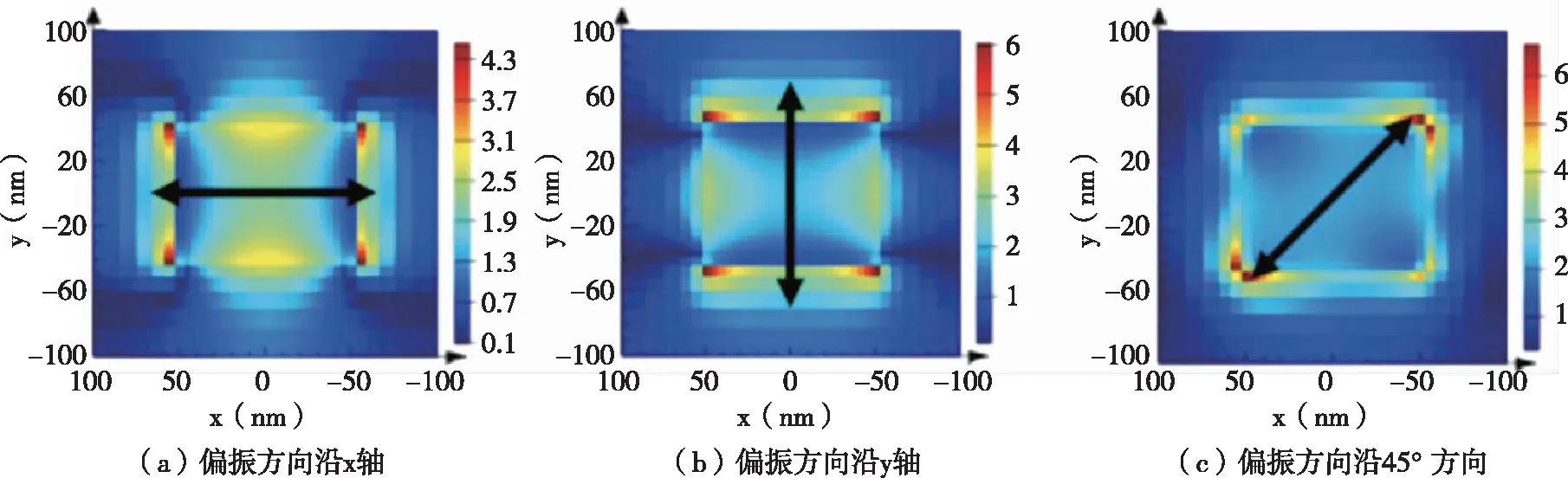

图3 亚波长结构波片近场电场分布图

我们由仿真计算可以得到出射光含有电场强度以及偏振相关信息的数据，然后利用三角函数表示法对相关数据进行分析。对于一个性能较好的

λ

/4波片需要满足正交方向相位差值为π/2和电场强度之比绝对值为1这两个条件。图4给出在不同波长下，辐射光在

x

和

y

两正交方向的相位差值及

x

、

y

方向电场强度绝对值之比(|

E

|/|

E

|)。图中左侧纵轴表示电场强度值之比，右侧纵轴表示相位差值。由图4看出，当正交方向相位差值的误差控制在±2°时，在一个较宽的波段范围内可以获得近似平滑的π/2相位差值。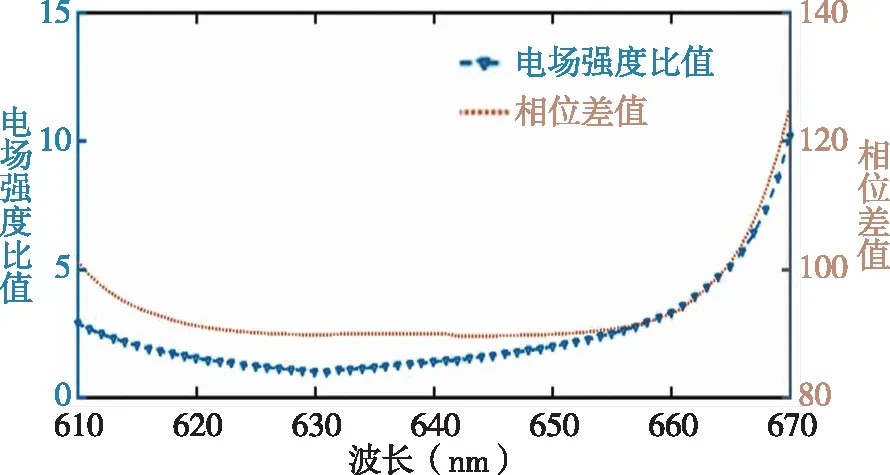

图4 不同波长下正交方向相位差值和电场强度比值

3 性能分析结果

在实际的原子频标光学模块构建中，会广泛的使用

λ

/4波片，其主要作用是对入射光的偏振态进行调控。依据使用的条件和需求，对光学器件的优劣制定出一系列的评价标准。在完成器件的设计后，需要对其性能进行仿真计算分析。根据上述方案原理，我们主要对该结构波片的消色差波段带宽、透过率、偏振调控特性等性能进行分析。

3.1 消色差波段带宽

在某一波段范围内，若

E

与

E

两正交方向的相位差值都近似为π/2，且每一对应波长处|

E

|与|

E

|之间的比值都近似为1，那么这种矩形银纳米棒结构波片在该波段称为消色差波片。在前文中已经证明可以通过改变偏振角的大小来调节|

E

|与|

E

|之间的比值。如图5所示当光线正入射时，不同波长下对应的相位差值。当相位差值的误差控制在±2°时，消色差波段为620nm～668nm。意味着在此波段范围内亚波长结构波片都满足消色差波片的要求，但针对不同波长入射的情况下，若想调制出圆偏振光，则需要适当改变入射光的偏振角度。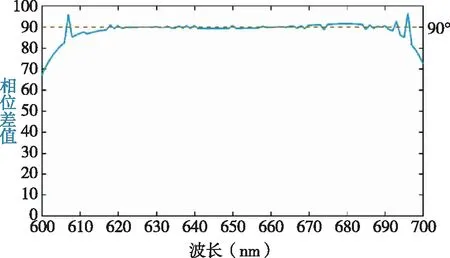

图5 不同波长下的相位差值

3.2 消色差波段透过率

透过率是评价光学器件性能的重要指标。本文主要对消色差波段的透过率进行探究。如图6所示，可以看出波长不同时透过率也不同，在620nm～668nm的消色差波段透过率是不断升高的，最低的透过率高于40%，最高的透过率为48%左右。但需要考虑实际加工后的器件透过率可能会降低，因为仿真计算是在理想条件下进行。

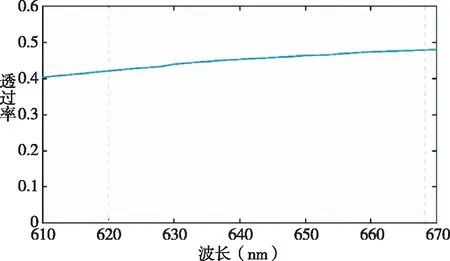
图6 不同波长下的透过率

3.3 偏振调控特性

通过调节入射线偏振光的偏振方位角，可以调制出多种偏振光，调制示意图如图7所示。

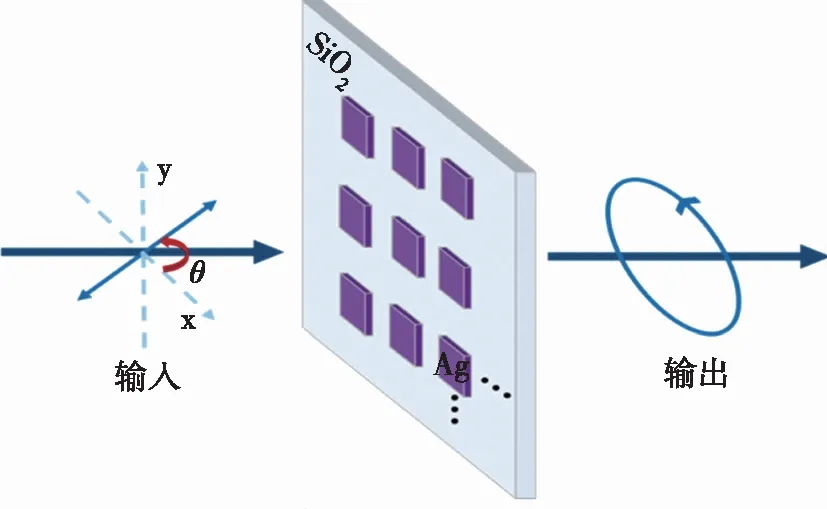
图7 偏振态调控示意图

采用此结构的消色差波片通过仿真计算实现了入射线偏振光到圆偏振光及椭圆偏振光的转换，如图8所示列出入射光的偏向角及出射光的偏振态，出射光偏振态参数见表1。在入射波长为633nm时，入射线偏光的偏向角为±45、±135时，出射光为圆偏振光；偏向角为其他角度时输出光为椭圆偏振光；偏向角为0、90、180、270时输出光依然为线偏振光。若将波片加工封装之后，亦可固定入射线偏振光偏向角，通过旋转封装结构来调控输出光的偏振态。因此该新型亚波长结构波片可以调控出多种偏振态的出射光，也为光频原子钟的小型化、集成化奠定了基础。

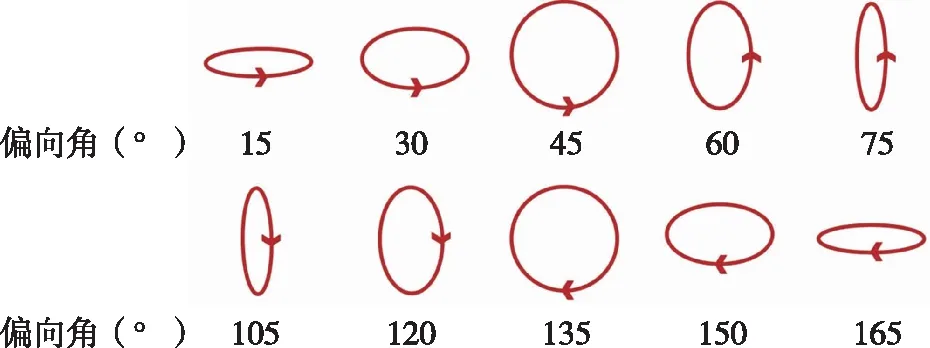
图8 出射光的偏振态

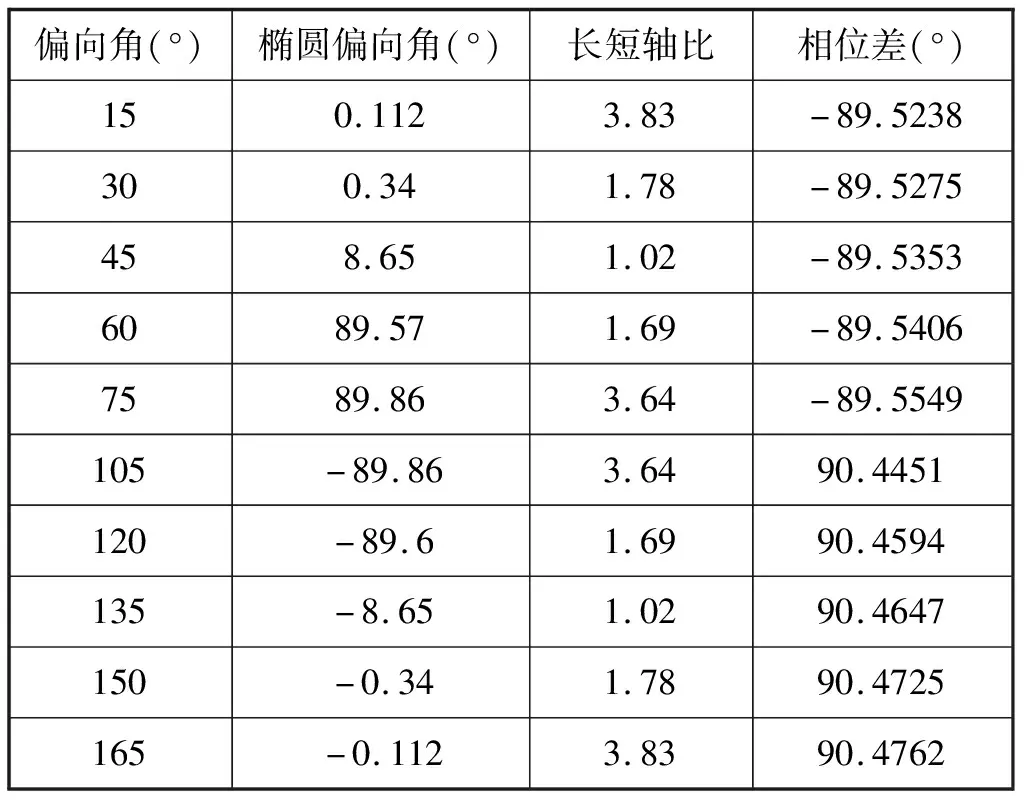
表1 出射光偏振态参数

4 结束语

综上，本文设计出一种矩形银纳米棒结构波片，对其结构模型进行仿真计算，可以在远场实现光场偏振态的调控。利用时域有限差分数值方法进行仿真模型的计算与误差容限的分析，为实际器件的加工提供了一定的参考限度。与此同时也对该结构波片的性能和偏振特性进行了分析。利用线偏振光垂直照射波片结构表面，当相位差值的误差控制在±2°时，消色差波段为620nm～668nm。与此同时在此消色差波段透过率是不断升高的，最低的透过率40%，最高的透过率为48%左右，这是可以与传统双折射晶体波片相比拟的。基于该结构体积小、厚度薄、灵活度高，将其应用于光频原子钟系统中，有利于光学调制模块集成化、小型化的实现，有利于辅助激光器调制出高效的偏振光。