基于信任模型的分簇WSNs可靠数据采集方法*

陈 辉张春雨

(安徽理工大学计算机科学与工程学院，安徽 淮南 232001)

无线传感器网络WSN(Wireless Sensor Network)在军事、医疗和工业等方面有着广泛的应用，集中体现在数据收集和事件监测方面[1-2]。然而，无线传感器节点多为电池供电，计算能力和带宽容量有限，且经常部署在一些恶劣的环境中。这些因素极易导致节点出现异常和受到干扰，进而造成监测数据的可靠性得不到保障[3]。无线传感器网络是以数据为中心的网络，对突发事件的快速响应和数据的可靠采集是非常必要的[4-6]。

通常WSN中异常数据一方面由于节点自身故障或外界环境干扰引起的数据异常；另一方面由突发事件引起的数据变化超出正常幅度。前者直接关系着网络监测数据可信度，而后者则是无线传感器网络监测重点，因此WSN数据异常检测和可靠性传输很有必要[7]。无线传感器网络中异常数据检测通常借助统计学方法或充分利用邻近节点之间的空间相关性。如文献[8]基于隐马尔科夫模型的数据异常检测方法，以先验数据为参考判断新产生的数据轨迹偏差，但阈值的设定需要大量数据支撑；文献[9]利用K-Means均值聚类对异常数据进行分类，对所有数据对象依据相似程度进行划分，该方法更适合集中式异常检测，对所有数据进行聚类算法复杂性较高。数据采集是无线传感器网络主要功能之一，而采集数据的可靠性直接决定着网络的安全运行[10]，但仅对异常数据进行筛选还不能完全满足对无线传感器网络数据可靠性的要求。无线传感器网络中数据来自众多传感器节点，因此，传感器节点的可靠性是影响数据采集可靠性重要诱因之一，而信任模型的出现解决了传感器节点路由选择、数据认证等方面问题，为节点可靠性判断提供了理论支撑。目前，信任模型已广泛应用在无线传感器网络领域[11-13]，其中，文献[11]通过信任模型帮助寻找可靠的节点，提高了节点之间的协作和系统的性能；文献[12]提出一种基于时间因素的WSN信任模型，利用动态反馈机制计算节点信任度，同时引入时间衰减模型降低网络时延、增加模型可信度；文献[13]在直接信任度计算时使用异常衰减修正贝叶斯方程，并以熵作为参考为节点信任度赋权，很好地克服了主观赋值的局限性。此外，借助UAVs(Unmanned Aerial Vehicles)[14-15]可较为准确验证数据可靠性，但UAVs使用成本较高。当前WSN数据采集多以去冗余、降能耗为目的，如文献[16]用历史数据来降低冗余数据的采集，该算法只有在监测区域数据波动较小的情况下效果较好；采用压缩感知(Compressed Sensing)技术[17-18]对数据进行采集，能有效缓解硬件资源的压力，但压缩采集会导致部分数据的失真。而随着物联网应用要求的不断提高，如车联网、自动驾驶等，感知层数据可靠性变得尤为重要。

在实际应用中传感器节点一般以恒定频率进行数据的采集和传输，多数情况下数据是缓慢变化的，如温度、湿度、压力等。这种情况下“不可靠节点”的存在直接影响着检测结果的准确性，因此节点可靠性和数据可靠性的准确判断关系到网络的QoS(Quality of Service)。基于多数节点出现“数据异常”为突发事件所致，少数节点出现“数据异常”一定概率上是节点异常或干扰所致的事实，本文提出一种基于信任模型的数据收集方法(Algorithm of Trust-based Data Gathering，AT-DG)。该算法以分簇型网络拓扑结构为基础，首先，基于数据时间相关性和空间相关性区分数据异常与否，并统计异常数据占比。然后，根据异常数据占比的不同采取不同的数据采集策略。对于少数“数据异常”，通过簇首节点信任评估机制判断节点可信度，进而得出异常数据产生原因，并采取相应的采集策略；对于多数“数据异常”，启动监测事件发生时的数据采集机制，实现紧急数据包的采集和传输。AT-DG算法在保证一般数据可靠收集的同时，可实现监测事件发生时的快速响应。

1 网络模型

分层的WSN网络拓扑结构因其简单高效便于管理广泛应用在各种监测活动中。相邻传感器节点按照一定规则进行组合，形成一个“簇”，如图1所示。每个簇都有一个簇首和若干成员节点组成，并且簇间成员节点感知覆盖区域有一定重合。另外，同一簇内的成员节点在通信行为和空间特征上具有较高的相关性，这也使在簇头建立信任模型成为可能。同时，事件的发生也表现为部分簇内数据变化差异较大，以簇为单位的异常检测机制更容易实现。

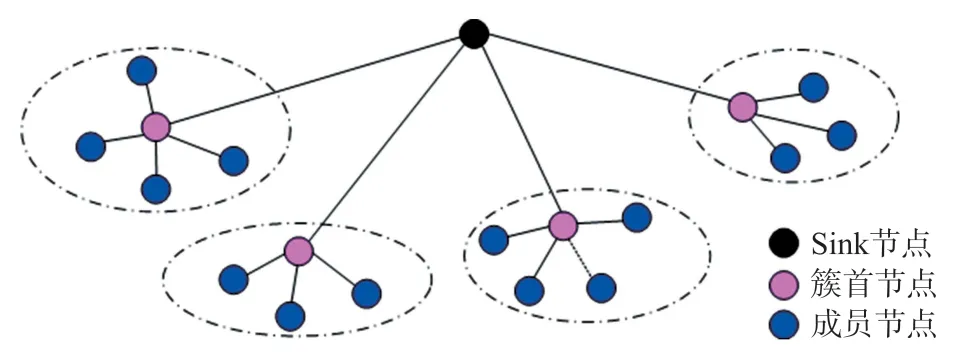
图1 分簇的网络拓扑结构

本文依据HEED协议对网络进行层次划分，且网络中传感器节点满足以下条件:①网络中节点位置一旦确定就不在移动，且每个节点都有唯一的标识；②网络中只有唯一的Sink节点，网络中数据路由由簇首直接或间接地发送到Sink节点；③簇内各成员节点位置相邻且只能和本簇簇首通信；④每个节点通信半径、路由能耗相同且能源不可再生。

2 数据采集方案

2.1 数据异常判别和采集规则

通常情况下，如果簇内多数节点监测数据发生突变，监测事件应当是大概率发生，而少数节点监测数据发生突变很大程度上是采集数据错误。因此，可以通过设定异常数据占比的阈值来区分异常数据是监测事件发生还是错误数据。对于异常数据的判断，统计学中采用基于距离的方法可对异常数据进行定义，即数据前后变化的差值[19]。为了突出异常数据的变化量和异常数据的占比，阈值的设定首先要针对数据变化量的定义，然后再判断这些节点占的比重，进而判断是事件发生还是数据错误。数据级异常检测通常利用节点数据流的时间性和空间性等特点，通过比较当前异常数据与历史数据、邻节点数据差异，进而计算节点信任度。数据异常检测方法中基于分类的方法由于其检测精度受到数据集规模的影响，不适合在资源受限的无线传感器网节点实现，而基于统计的异常检测更符合无线传感器网要求，其中四分位数展布法计算量小且收敛速度快，因此文中选用四分位展布法的箱型模型作为异常检测的依据。

基于监测数据的时间相关性设置大小为M的数据窗口，如图2所示。对于节点i，当前时刻t采集的数据为a i(t)并记t＝n×Δt，Δt为采样间隔，则上一时刻，即(n-1)×Δt时刻采集数据为a i(t-1)。簇首利用箱型模型，即式(1)对节点i前M-1个数据进行箱型计算并划分可信区间[εa，εb]。如果a i(t)在[εa，εb]区间外即数据偏差过大判断为异常数据。

图2 基于箱型模型的数据异常判断

式中:Q1和Q3分别为M-1个数据中下四分位和上四分位值，在计算分位时采用向下取整策略来确定Q1和Q3的值。其中IQR＝Q3-Q1。通过历史数据对簇内各节点进行区间划分，以该区间作为当前时刻数据异常的判断依据。

监测事件的发生主要表现为局部性数据变化，而事件规模大小与数据变化节点个数成正相关。因此，数据异常占比θ可定义为数据异常节点数与簇内总结点输之比。

式中:N为当前时刻簇首基于式(1)统计出该簇内数据异常节点数，NCH为该簇内成员节点总数。由于算法基于网络异常规模的大小为采集依据，并且监测事件的发生具有小概率性和局域性，为了研究方便本文取¯θ＝0.25为规模阈值。在实际应用中，可根据监测系统的性能来调整¯θ取值。依据θ值的不同，数据采集规则如下:①当0<θ<¯θ，小部分异常值出现，可能由节点异常引起，采用基于信任模型的采集方式；②当θ≥¯θ，多数节点出现数据异常，可能由事件发生引起，启动紧急数据采集机制。

2.2 基于信任模型的节点筛选

对于少数节点出现数据异常有可能是节点故障导致的，但也不排除由事件发生引起的数据异常。为此，对于出现数据异常的节点要从节点和数据两方面进行考虑，通过节点信任度[20]和数据偏移量的计算，为可靠性数据采集方案提供理论依据。

2.2.1 节点信任度计算

节点的通信质量是数据可靠性重要保障，节点级信任度可利用簇内节点通信行为和数据相关性进行计算。基于文献[10]和[13]所利用的Bayes信任管理框架同时对beta分布进行拟合，利用节点中历史交互记录计算节点可信度。通过已知条件概率密度参数表达式和先验概率，结合贝叶斯公式可以为后验事件提供决策。则节点i和节点j信誉分布reputationij可表示为:

式中:α和β分别表示节点i和节点j历史交互成功和失败次数。节点交互历史及邻节点的相似程度作为节点故障的主要依据，由贝叶斯评估方法可得节点i关于节点j概率密度分布函数为:

式中:φi j为交互成功的概率，且α>0，β>0，则对于簇首节点j和异常节点i，在成功交互a ij次 和失败交互βi j次 时，簇首对异常节点i的可信度可表示为:

2.2.2 数据偏移度计算

在节点可信度计算的基础上，引入数据偏移度来提高采集模型准确性。数据偏移度是指节点当前监测的数据同历史数据以及邻节点数据的偏差程度，通过异常节点历史数据和邻节点数据进行计算。对于异常节点i的数据偏移度的计算过程是:选取同簇通信半径内k个邻居节点，设k个邻节点当前采集数据为a i1，a i2，…，a i k，则邻节点数据均值为:

同时对于异常节点i在窗口内取当前时刻前M-1个历史数据，历史均值为E i，则异常节点i的数据偏移度为:

式中:a i为异常节点i当前采集的数据，ω为平衡系数且ω∈[0，1]，ω的大小决定了历史数据和邻节点数据的权重。

2.2.3 异常数据节点综合信任度计算

对于数据异常节点的判断要综合考虑节点本身的质量和数据偏移程度，式(5)和式(7)分别给出了节点质量和数据偏差的定义。节点信任度越高且与周围节点数据偏差越小，该数据异常节点可靠性就越高。异常节点i的综合信任度Trusti可表示为:

式中:φ为平衡系数且φ∈[0，1]，而节点信任度是一个逐渐积累的过程，所以在更新当前时刻信任度时需要考虑前一时刻节点信任度值，即当前信任值，其中κ为平衡系数，为前一时刻节点信任度。当异常节点i的综合信任度大于阈值λ时，采信该节点数据，启动紧急数据传输机制；当小于阈值λ时，数据可信度较低，过滤该节点数据。

2.3 紧急数据可靠传输机制

目前，对于数据可靠传输机制的研究主要从拥塞控制和可靠性保障两方面入手。突发事件会引起数据激增，而簇首缓存空间有限，大量数据的涌入会造成队列溢出，导致数据包传输时延和丢包率急剧增加。因此，针对紧急情况下突增数据流，需要充分利用整个网络资源来确保紧急数据的可靠性传输。另外，分簇结构下各簇首在数据传输过程中存在着的链路竞争和数据冲突也关系着紧急数据可靠性传输问题。

基于以上突发事件数据流特点，提出一种冗余协助传输机制(Redundant Assistance Mechanism，RAM)。RAM充分利用处于正常状态下的簇首资源，基于紧急数据优先的路由思想，该方式保证了紧急事件的准确感知和及时预警。具体RAM工作流程如下:

Step 1 簇首检测到异常节点信任度高或异常节点超过规模阈值时，立即启动紧急数据传输机制；

Step 2 簇首节点采用多链路传输策略，向其下游发送紧急请求，请求信息包含该簇位置信息；

Step 3 下游簇首节点接到请求消息后，降低自身簇内数据采集频率和减少其他簇首数据转发，并提高请求簇首数据转发优先级来确保紧急簇首数据传输；

Step 4 异常数据采集完毕，各簇首恢复正常采集机制。

RAM通过提高紧急簇首优先级并降低下游簇首采集频率来满足紧急数据传输需要，如图3所示。RAM机制虽然牺牲了部分层次的数据采集，但可以最大程度地保障网络对突发事件的及时上报和处理。实际上突发事件的频率较低，该机制的设置对网络整体性能的影响并不大。

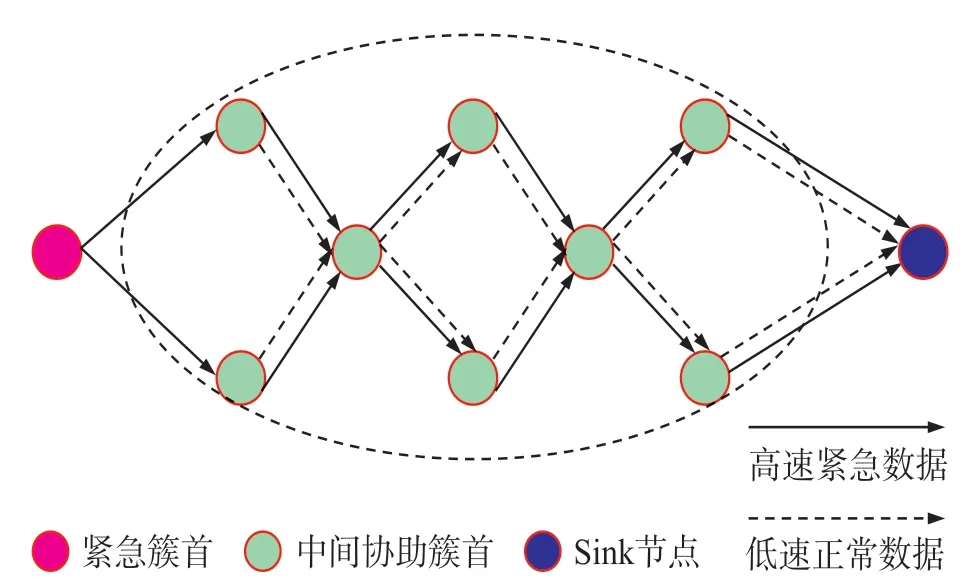
图3 紧急数据传输机制

2.4 数据采集方法

无线传感器网络最为重要的是当监测事件发生，如森林火灾、瓦斯泄漏等而引起的数据流异常时，传感器节点要能够准确感知、快速传达到汇聚节点。因此，为了保证监测事件发生时，监测数据能够及时可靠传输和收集，可采用差异化的数据收集策略。

无线传感监测网络中“异常数据”的出现可能是由节点故障产生的错误数据，也可能是事件发生引起数据突变。由于传感网的监测数据大部分都是重要程度较低的冗余数据，这些数据之间的差异较小，“异常数据”主要表现为少数节点出现数据异常，而事件发生引起的极富价值的“异常数据”表现为多数节点的数据异常。通过异常数据占比阈值的划分来判断“异常数据”类型，对前一种数据异常采用基于信任模型的采集方式，对后一种数据异常启动紧急数据采集方案。

因此，对于正常的普通数据采用常规的数据传输方式，对于异常数据，根据异常数据占比情况，采用过滤方式或紧急传输策略。异常数据占比低于设定的阈值，采用基于信任度模型的过滤机制，异常数据占比超过设定的阈值的异常数据，采用紧急数据传输策略，数据采集方案如图4所示。

图4 数据采集方案

3 仿真与性能分析

为了验证AT-DG算法数据采集的准确性和及时性，本文使用MATLAB作为仿真工具验证算法相关性能。在100×100矩形区域随机分布传感器节点，基于HEED协议对网络进行层次划分。相关仿真实验参数配置如表1所示。

表1 仿真实验参数

3.1 信任模型性能分析

基于信任度的数据异常类型的判断是AT-DG算法的基础，本文的信任度模型基于节点交互和数据偏移两个维度进行建模，利用信任度区分数据异常节点正常与否。因此，是否能够有效检测出非正常节点是衡量该模型的重要指标。结合本文以数据异常为导向的信任评估，算法的检测率定义为检测出的异常节点占总异常节点的比例。为了验证信任模型的有效性，实验中设置150个传感器节点，依据HEED协议对网络进行层次划分，在不同的异常节点占比下对本文算法和经典信任模型RFSN[21](Reputation based framework for sensor networks)的检测率进行对比，结果如图5所示。随着网络中异常节点比例增加，AT-DG和RFSN检测率均呈现下降趋势，但AT-DG算法以数据和节点质量为依据，平均检测率比RFSN算法高出9.14左右%。

图5 检测率对比

此外，选取在异常节点占比15%时随机选取一个簇，检测该簇内正常节点和异常节点信任度均值变化趋势。实验过程中异常节点随机分布在网络中，正常节点可准确上报环境中的数据，簇内所有节点属性相同并设初始信任度为0.5。实验选取前50个采样周期该簇内节点信任度均值变化，如图6所示。其中，前15次采样中，由于正常节点和异常节点报告数据差值较大，信任度区分效果不明显；随着采样次数的增加，异常节点不良行为造成可信度降低，进而导致异常节点信任度均值逐渐下降，而正常节点始终表现良好。由此说明，基于信任模型可以较好的区分异常数据节点的类型，为数据可靠性采集提供决策支撑。

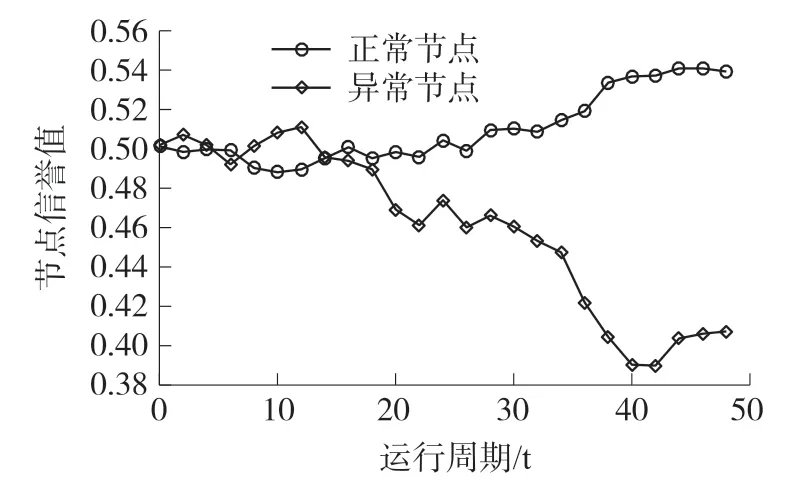
图6 节点信任度对比

3.2 网络性能分析

为了验证AT-DG算法数据采集性能，在数据采集准确率和网络能耗与原生HEED算法进行试验对比。图7是数据采集准确率对比，试验时随机选取一个簇模拟事件发生，对正常节点和异常节点数据包进行标记，统计Sink节点接收到正常节点数据量占总数据量的百分比作为试验结果。试验对比前20次采用结果进行对比，HEED协议数据包准确率受异常节点影响平均准确率为71.75%左右。而AT-DG算法加入异常数据检测机制，对异常节点数据包进行过滤，随着仿真轮次的增加，平均准确率维持在91.73%左右，较原生HEED协议平均数据采集准确率高20%左右。

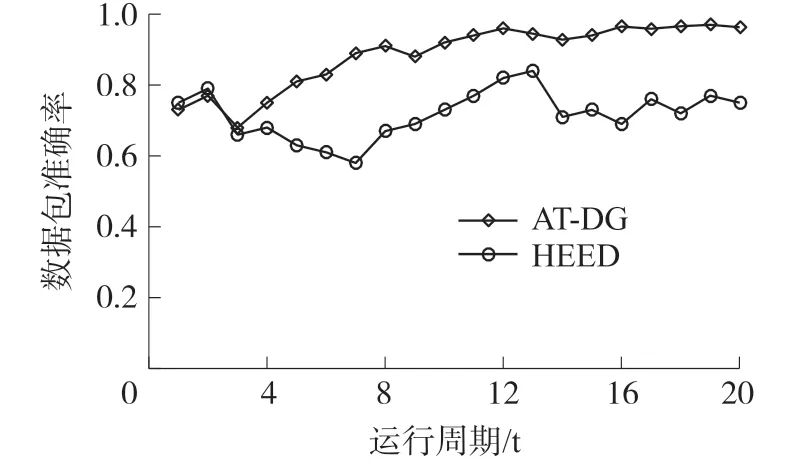
图7 数据包接收准确率对比

图8是AT-DG算法节点总能耗变化曲线。从图8可以看出在相同的轮转周期内，AT-DG总能耗小于原生HEED算法。其中，HEED协议在2 200轮次时网络总能耗已经达到最值(节点全部死亡)，而AT-DG算法下网络生命持续到3 200轮次。此外，AT-DG引入紧急数据传输机制，避免了因突发事件引起大规模数据传输，均衡网络负载，节点出现死亡现象较HEED协议迟200轮次左右。以上表明AT-DG能量利用率更高，网络寿命更长。

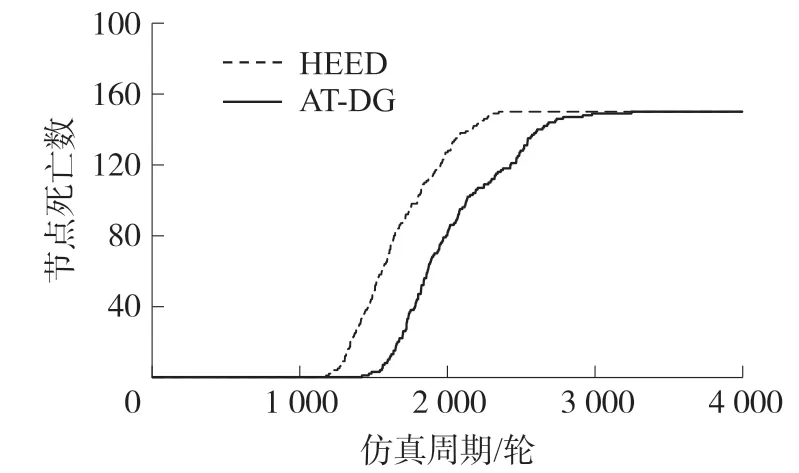
图8 网络总能耗对比

4 结束语

为了解决因数据异常造成的决策误判问题，本文基于分簇的无线传感器网络拓扑结构，结合事件监测特点，以异常数据为出发点设计了AT-DG数据可靠性收集算法。通过建立异常数据节点的信任度模型，计算异常数据节点的信任度，对节点异常类型进行判断，进而采取相应的数据采集机制。仿真结果表明AT-DG算法在事件监测中能够精准、及时对数据进行处理，该算法可广泛用于层次型无线传感器网络数据的采集当中以提高监测数据采集的可靠性。