复合封装高量程加速度计参数动态辨识方法*

温晓杰石云波*赵 锐曹慧亮王彦林张娟娟

(1.中北大学电子测试技术重点实验室，山西 太原 030051；2.西安机电信息技术研究所，陕西 西安 710065)

现代战争为信息化的战争，精确制导、引信侵彻日渐成为战争火力的主要打击方式，为了满足逐渐发展的战争的需要，各国都在大力发展尖端武器[1]。其中量程达到数万gn乃至数十万gn的加速度计作为将其他信号转化为电信号的器件在引信制导过程中占据着举足轻重的位置[2]，精确测定加速度计的动态性能指标可为智能控制、钻地武器的研制奠定重要的基础[3]。而在实际应用中，加速度计在高量程的测试环境下的动态特性会发生变化，从而影响测试精度[4]。由于高量程加速度计具有较高的固有频率，对于激励信号的要求极其苛刻[5]，对其精确度的测量将是一个巨大的考验，因此需要通过系统辨识的方法来获取高量程加速度计的内部传递特性，进而对其工作频带及谐振频率进行校准。

对加速度计动态系统进行系统辨识是对加速度计动态建模的一种手段，常用的系统辨识方法有预测误差法、神经网络法、遗传算法等[6-7]，其中预测误差法将加速度计构建为ARMAX模型，将对加速度计模型各阶系数的辨识转化为对加速度计内部结构的相关参数辨识，降低了辨识的维度，当加速度计模型阶次较高时，计算量相对较大且采用高斯牛顿迭代法求解容易陷入局部最优，无法得到全局的最优值，神经网络法同样在全局寻优的过程中容易陷入局部最优值，虽然结合遗传算法可以大大降低这些缺陷，得到了比较精确的结果，但大多学者仅仅将加速度计视为简单的二阶系统，但实际的加速度计由于封装、安装等方面的原因，往往表现为高阶系统。

本论文从高量程加速度计的多层封装出发，分析加速度计的内部结构，确定需要辨识的加速度计模型参数的数量，然后基于PSO-BP算法，分析加速度计的辨识原理，将PSO算法运用到BP神经网络算法中，针对BP算法的收敛速度慢和易陷入局部极值的局限性进行了改进，大大提高收敛速度，并克服局部最优值所造成的的误差，并采用惯性权重线性递减、学习因子非线性变化的方法，提高算法收敛速度和模型辨识精度，最后通过数值仿真和实验的方法验证该算法的可行性。

1 加速度计动态校准理论

1.1 加速度计数学模型

高量程加速度计相对于普通加速度计具有更高的谐振频率，为了提高抗过载能力，往往采用复合封装的方法对加速度计进行防护[8]。高量程加速度计的复合封装结构如图1(a)所示，硅芯片和玻璃衬底通过阳极键合到一体，然后通过贴片胶粘贴到外壳底部，周围再用灌封胶进行填充，其每一个部分都可以看做是一个二阶系统，那么整个高g加速度计可看成多个二阶系统的串并联的组合。高量程加速度计的整体封装结构的振动模型如图1(b)所示，整体模型可等效为一个三自由度振动系统，该系统有三个谐振频率。高量程加速度计是由各个部分串并联而来的，整体构成了一个六阶系统。

如图1(b)所示，c i、k i、mi(i＝1，2，3)为各层二阶系统的阻尼系数、刚度系数和等效质量，加速度计整体模型可视为三个二阶系统的串联组合，其标准传递函数为:

图1 复合封装加速度计结构示意图

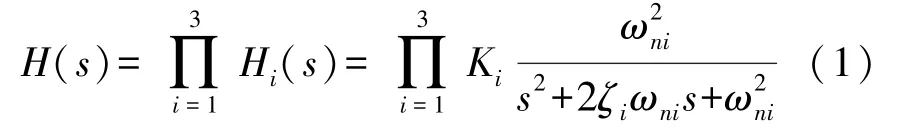
式中:H i(s)为各层系统传递函数，K i为各层系统函数增益，为各层系统的无阻尼振荡频率为各层系统阻尼比。

因此，复合封装高量程加速度计模型传递函数为:

将传递函数分子分母系数拼接为待辨识参数向量θ＝[b0b1…b ma0a1…a n]。

高量程加速度计的动态特性的指标意味着能即时准确复现输入加速度信号的能力，分为时域动态指标和频域动态指标。本论文着力于实现对高量程加速度计频域动态指标的校准，主要通过对高量程加速度计系统辨识的方法来实现对其通频带和谐振频率的校准。

1.2 窄脉冲动态校准理论

动态校准的目的是获取被校系统的全部工作模态，这对激励信号就提出了相关要求，动态校准的理想激励信号的频谱在所有频率点上的都具有平直的幅频特性，其时域信号为冲激信号，这在物理上是无法实现的，因此提出在有限带宽内保持平直的准δ信号作为激励信号，根据文献[5]中窄脉宽校准准则，激励信号脉冲宽度和需要校准的加速度计的谐振频率有如下关系:

式中:τ激励加速度脉宽；f为脉宽为τ的激励加速度信号能校准的最大谐振频率。

一般实验室的校准装置，可产生的最小激励加速度脉宽为20μs左右，通过式(3)可计算能校准的加速度计最大谐振频率为70 kHz，对于复合封装加速度计，最高阶的芯片本振频率高达400 kHz～500 kHz，要想将加速度计全部模态激发出来，所需最大激励加速度脉宽为2μs～3μs，这在现有的校准技术和实验条件下是难以实现的，因此本文通过动态参数辨识的方法，建立加速度计的多阶动态模型，利用BP-PSO算法对加速度计的模型参数进行系统辨识。

2 基于BP神经网络原理的改进PSO算法

2.1 BP神经网络

BP神经网络是1986年由D.E.和J.L.提出的一种多层前馈网络的误差反向传播算法，该算法由输入层、隐含层(一层或多层)和输出层构成，其网络拓扑结构如图2所示，其中输入层为待辨识参数θ，一方面对样本进行前向传播，另一方面通过对比模型输出与期望输出的误差来进行反向馈通传播，通过误差一次次调整每一层的权重继续进行前行传播，通过对样本的训练一次次逼近输出期望值。

图2 BP神经网络拓扑结构示意图

为了提高BP神经网络的泛化能力，采用基于全局误差的BP神经网络辨识，模型的稳定性和准确性可以通过误差序列的平均值M和标准差(即均方差σ)来进行描述:

虽然误差平均值和标准差可以反映模型预测和实际数据的拟合程度，但是计算量较大，因此本文采用误差的残差平方和(即均方误差)MSE(Mean Square Error)来进行描述[9]。

MSE越小表明系统辨识效果越好，这样就将求极值转化成一个二次规划问题，为了方便计算，我们引入模型系统辨识的代价函数J，令

为使代价函数J最小，使用梯度下降法对参数进行迭代求解，梯度下降法是一种最速下降寻优法，每一次的迭代只考虑下一步的方向，而忽略前面所积累的经验[10]。除此之外，BP神经网络的学习因子对辨识结果的影响也很大，当学习因子较小时，收敛速度太慢，久久得不到预期的结果，当学习因子较大时，又容易跳过最优值，并来回震荡，甚至会使迭代结果发散，致使辨识失败，而且当初始参数选择不当时，还容易陷入局部最优值的困境，因此本论文在BP神经网络算法的基础上引入了PSO算法，从BP网络的不足之处入手，来对算法进行改进。

2.2 基于BP神经网络的改进PSO算法

PSO算法(Particle Swarm Optimization，粒子群优化算法)是1995年由Eberhart和Kennedy两位博士提出来的，如今已被应用到神经网络训练/模糊系统控制和人工智能等领域[11-12]。其核心思想为每个粒子在每次运动过程中在自己上一次的位置、自己经历的最优的位置p ibest以及所有粒子经历过的最优位置gbest三个因素的共同作用下调整自己的速度和方向，第i个粒子在k+1时刻的速度和位置为:

式中:ω为惯性权重系数，表征粒子在每一次移动时，上次的状态所占的比重；c1，c2分别为个体学习因子和全局学习因子；r1，r2为分布在0～1之间的随机数；p ibest(k)为第i个粒子在前k次的运动过程中最优值(个体最优值)；gbest(k)为所有粒子在前k次的运动过程中的最优值(全局最优值)。

惯性权重ω是由shi等人在1998年提出来的[13-15]。并且提出了惯性权重线性递减的粒子群算法，ω较大时算法有较强的全局搜索能力，ω较小时算法具有较强的局部搜索能力，为了使算法在全局和局部的搜索中达到最佳的平衡和加快收敛速度，定义变化的惯性权重为:

式中:ωmax和ωmin分别为惯性权重的最大值和最小值，k和K分别为当前迭代次数和最大迭代次数。

对于学习因子，经过多数学者的理论论证和实践检验，当学习因子固定不变时，其收敛速度和迭代效果并不理想，纷纷提出各种学习因子随迭代次数而改变的粒子群算法，都得到了较为满意的效果[16-19]。经过前人的研究，个体学习因子c1逐渐减小，全局学习因子c2逐渐增大，会提高算法的收敛速度和迭代精度。

虽然改变学习因子会提高算法的计算速度和准确度，但线性改变学习因子的方法，也在一定程度上存在缺陷，理想的学习因子在初期和末期变化应该变化缓慢，为了更大程度地搜寻更为广阔的位置以及持续以更快的速度进行局部探索，提高算法的精度，而在算法中期，学习因子应该快速变化，尽快从全局寻优转移到局部寻优上，因此本文提出学习因子非线性变化的粒子群算法，学习因子可按照sigmoid函数或cos函数进行取值。

若按照sigmoid函数，学习因子随迭代次数变化的表达式为:

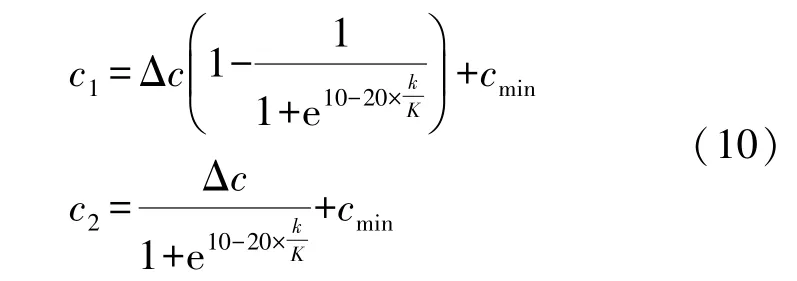
式中:cmax、cmin分别为给定学习因子的最大、最小值，一般取[1，3]；Δc＝cmax-cmin；k为当前迭代次数；K为最大迭代次数。

若按照cos函数，学习因子随迭代次数变化的表达式为:

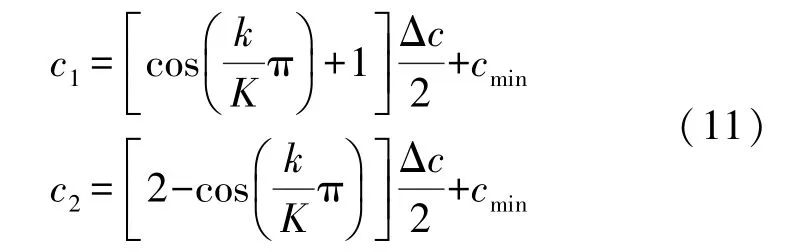
经过数值仿真比较，本论文选用sigmoid函数作为学习因子的变化函数，改进的算法流程如下:

Step 1 随机产生n组BP神经网络各部分权重初始值ωi j、ωl并进行反向传播训练，根据图2网络结构将每一次的训练结果＾ωij、＾ωl经过式(12)后得到θ作为PSO算法的参数初始值，其中θi为θ中第i个参数，则初始粒子群位置为x(n，d)，d为参数的维度，设定历史权重ω和学习因子c1、c2向量；

Step 2 将BP神经网络中的代价函数J作为PSO算法的适应度函数，最优值即为代价函数的最小值，代入各粒子的初始位置计算各粒子的适应度，初始化粒子群的个体最优值pbest和全局最优值gbest；

Step 3 通过公式更新粒子新的位置和速度信息，通过计算适应度函数更新个体最优值pbest和全局最优值gbest；

Step 4 判断适应度函数J是否在精度要求范围内或是否达到最大迭代次数，若是，则进入下一步，否则返回step3继续迭代计算；

Step 5 输出的全局最优值gbest即为系统参数向量的辨识结果＾θ，将参数结果作为各阶系数即可转化为加速度计模型的离散传递函数H′(z)；

Step 6 通过零阶保持器将离散传递函数H′(z)转化为连续传递函数H(s)，并令s＝jw，即可求出系统的频率响应函数H(jw)；

Step 7 根据频率响应函数H(jw)可作出幅频响应曲线，并对结果进行分析，验证其算法的准确性和可行性。

3 数值仿真分析

为了验证上述算法对于高量程加速度计的参数动态辨识结果，利用MATLAB软件构建了基于实际加速度加加速度计的多阶动态模型以及激励信号进行仿真。

激励信号选用峰值为1μV，脉宽为100μs的半正弦加速度信号，持续时间段为600μs～700μs，其频谱截止频率为60.55 kHz，激励信号表达式为:

为了使仿真更加贴近实际，对于激励半正弦脉冲添加均值为0，方差为0.01的随机干扰，下面通过仿真来验证算法对加速度计模型参数的辨识效果。

假定加速度计为二阶系统(谐振频率为134.8 kHz)，待辨识参数θ＝[0.5，1.546×106，6.247×1011，1，1.026×105，7.08×1011]，其连续时间传递函数为:

将连续时间传递函数通过零阶保持器转化为离散时间传递函数，采样间隔为0.5μs，获得其离散系统传递函数为:

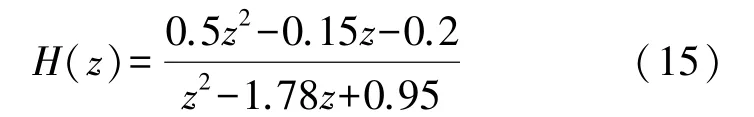
通过算法辨识得到其以分母最高阶系数为基准进行归一化处理后离散传递函数为:

再变换为连续时间传递函数为:

辨识得到的参数向量＝[0.5，1.546×106，6.247×1011，1，1.026×105，7.08×1011]，与待辨识参数向量θ相比，所有参数相对误差均为0%。通过算法获得加速度计二阶模型系统辨识的效果如图3所示。

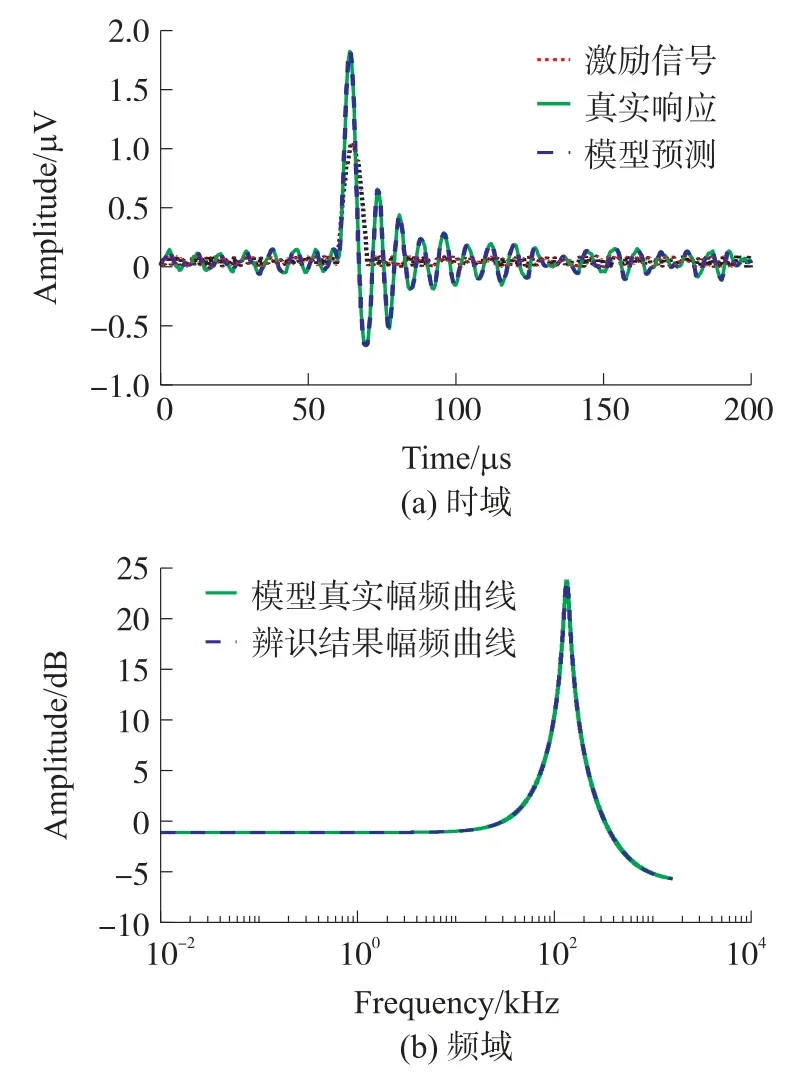
图3 二阶系统参数辨识数值仿真结果

假定加速度计为四阶系统(两个二阶系统串联，谐振频率分别为132.4 kHz、446.3 kHz)，其幅频特性曲线将呈现两阶谐振频率，其连续时间传递函数为:

将连续时间传递函数通过零阶保持器转化为离散时间传递函数，采样间隔为0.5μs，获得其离散系统传递函数为:

通过算法辨识得到其归一化离散传递函数为:

再变换为连续时间传递函数为:

各参数的辨识误差分别为1.40%、0.67%、0.05%、0.04%、0.12%、0%、0.71%、0.03%、0.02%、0.07。通过算法获得加速度计四阶模型系统辨识的效果如图4所示。

图4 四阶系统参数辨识数值仿真结果

假定加速度计为六阶系统(三个二阶系统串联，其谐振频率分别为83.2 kHz、254.4 kHz、417.6 kHz)，其幅频特性曲线将呈现三阶谐振频率，其连续时间传递函数为:

将连续时间传递函数通过零阶保持器转化为离散时间传递函数，采样间隔为0.5μs，获得其离散系统传递函数为:

通过算法辨识得到其归一化离散传递函数为:

再变换为连续时间传递函数为:

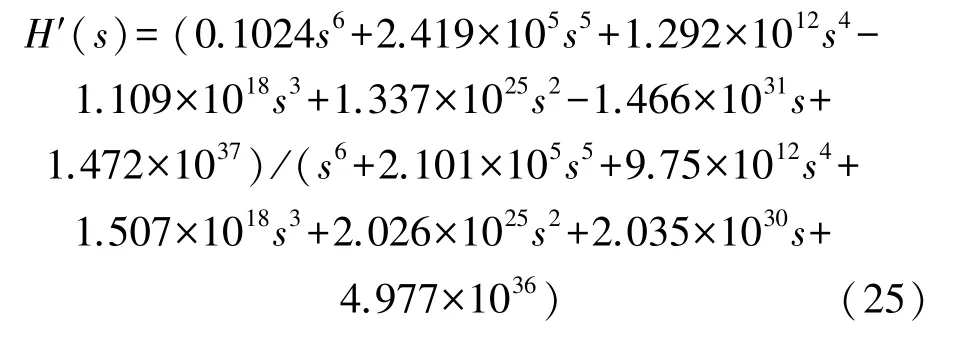
各参数的辨识误差分别为2.40%、2.46%、1.41%、4.07%、1.06%、2.88%、1.27%、0%、0.28%、0.04%、0.59%、0.05%、0.63%、0.14%。通过算法获得加速度计六阶模型系统辨识的效果如图5所示。

图5 六阶系统参数辨识数值仿真结果

由数值仿真结果可知，在输入信号有干扰的情况下，算法辨识结果良好，参数辨识相对误差都保持在5%以内，辨识结果时域和频域曲线基本完全重合，加速度计模型的各阶振型已全部辨识出来，工作频带与谐振频域与预定模型参数完全一致，满足动态校准的要求。

4 加速度计动态校准实验及数据分析

使用Hopkinson杆测试系统对中北大学研制的NCCJ-20型高量程加速度计(量程200 000gn，芯片本振频率450 kHz～500 kHz)进行动态校准测试实验。

Hopkinson杆测试系统示意图如图6所示，子弹在气压的作用下冲击Hopkinson杆，杆末端的加速度计在激励加速度作用下有信号输出，利用差动式多普勒干涉仪对激励信号进行复现，与加速度计的输出信号通过数据采集装置采集到上位机。

图6 测试系统示意图

在2 MHz的采样频率下通过系统辨识得到加速度计的归一化离散传递函数为:

变换为连续时间传递函数为:

激励加速度信号通过该模型的预测输出波形如图7所示。

图7 加速度计时域辨识实验结果

辨识结果模型的幅频特性曲线和实验数据FFT计算结果对比如图8(a)所示，由于实验过程中受到各种外在因素的影响，导致FFT的计算结果显得比较杂乱，但比较关键的频率点可以看出明显的峰值，其部分峰值所对应的频率点为加速度计的各阶谐振频率点。通过算法辨识出来加速度计模型三阶振动模态，分别是77.16 kHz、198.1 kHz、479.9 kHz，对应实验FFT计算结果中的75.56 kHz、207.1 kHz、489.5 kHz，其相对误差分别为2.12%，4.35%，1.96%。

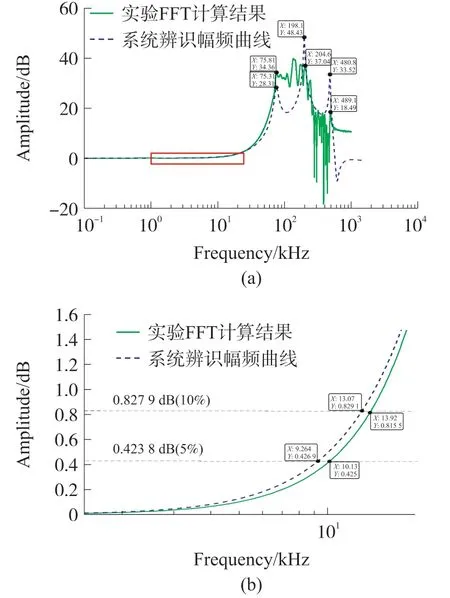
图8 加速度计频域辨识实验结果

为探究算法对加速度计工作频带的辨识结果，将图8(a)中方框部分放大，如图8(b)所示，在幅值误差在5%(对数幅值约0.423 8 dB)时FFT计算带宽为10.13 kHz，算法辨识带宽为9.26 kHz，相对误差为8.59%，在幅值误差为10%(对数幅值约0.827 9 dB)时FFT计算带宽为13.92 kHz，算法辨识带宽为13.07 kHz，相对误差为6.11%。算法辨识得到的加速度计谐振频率和频带宽度可信度较大，结果足以满足动态测试的要求。

5 结果与讨论

本文通过改进后的BP-PSO算法对高量程多振动模态加速度计进行了系统辨识。首先对施加被随机白噪声污染的半正弦激励加速度信号的加速度计多阶模型进行了系统辨识，得到了良好的辨识效果，最后利用Hopkinson杆校准装置产生脉宽20μs左右的激励加速度脉冲校准了芯片本振频率高达478.02 kHz的加速度计，此外也对加速度计的各阶振动模态和工作频带进行了校准，加速度计三阶谐振频率相对误差分别为2.12%、4.35%、1.96%，在5%和10%误差范围内工作频带的相对误差分别为8.59%和6.11%，得到了不错的动态校准效果。