基于网格模型简化算法的多传感测距误差自动修复研究*

轩春青

(郑州商学院信息与机电工程学院，河南 巩义 451200)

在多传感器测距过程中，常因出现环境遮挡和异常信号的噪音干扰[1]，导致测距技术的精度难以满足现实需求，因此对测距误差进行修复成为目前重要的研究方向[2]。

国内有学者提出一定的研究成果。如，黄科[3]等人提出基于统计理论的测距误差修复方法，该方法在统计理论的基础上通过单光子探测器的概率和激光雷达方程分析误差产生过程，利用单光子探测概率模型实现测距误差的修复。但该方法没有获取测距信息，存在检测误差概率低的问题。鞠萍华[4]等人提出基于双线性插值法的测距误差修复方法，该方法对侧头偏心误差、侧头各向异性等影响因素进行考虑，利用双线性插值法实现半径补偿，进而实现测距的修复。但该方法缺少构建网格模型，获取测距数据所用的时间较长，导致修复时间较长，存在修复效率低的问题。当前，国外有学者提出相关方法。文献[5]提出在无线传感器网络中，通过链路RSSI估计、温度补偿、PLE估计和节点间距离估计等方式，减轻路径损耗指数估计误差，提高测距的质量[5]。但该方法的测距精度受到的限制较多，难以广泛应用。

考虑到上述方法存在的不足，本文将网格模型简化算法应用在测距误差修复过程中，提出基于网络模型简化算法的多传感测距误差自动修复方法。针对传感器图像，利用RGB颜色空间构建网格模型，对网格属性及坐标进行归一化处理，并利用高斯滤波器减少颜色二次误差，将Huber残差代价函数实现测距误差的自动修复，其中，利用阈值调节因子控制测距误差修复残差，实现了高精度的多传感测距误差修复。

1 网格模型简化算法

在RGB颜色空间中，设ci(r i，g i，b i)、c j(r j，g j，b j)分别表示两种颜色。对颜色在网格中的差异进行评估，保证简化过程中网格的颜色。

利用RGB空间中的欧式距离对两种颜色之间存在差异D(c i，c j)进行计算:

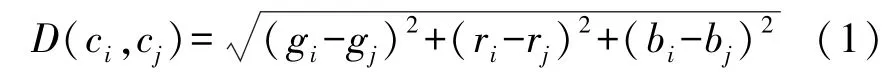
由于人对不同颜色存在差异性的视觉敏感度，因此计算色差时需要注意对三原色采取不同的计算方式[6]。为了对RGB空间的非均匀性进行补偿，通过加权颜色分量法计算色差D(c i，c j):

式中:w g、w r、w b均代表的是加权系数。

设(r，g，b)代表的是当前网格顶点v对应的颜色值，代表的是经过伸缩变化处理后顶点在网格中对应的颜色值。在此空间中可以通过欧式距离准确地对色差进行计算，逆变换处理目标点的颜色属性:

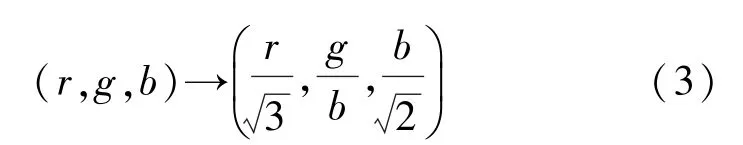
通过变换获得目标点对应的颜色属性，以降低光照和背景的颜色信息干扰。此时颜色分量的坐标信息产生变化，在计算折叠代价过程中为了平衡空间属性信息和空间位置信息，在网格数据进行初始化处理过程中，对网格属性及坐标进行归一化处理，使其变换后的范围均为[0，2][7-8]。

在网格模型简化过程中将包围盒的坐标范围设置为[xmin，xmax]，[ymin，ymax]，[zmin，zmax]，其中:

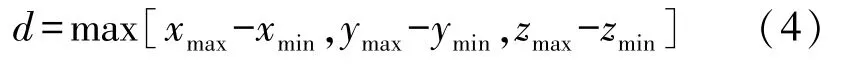
利用下述公式对模型中存在的点进行规整处理:

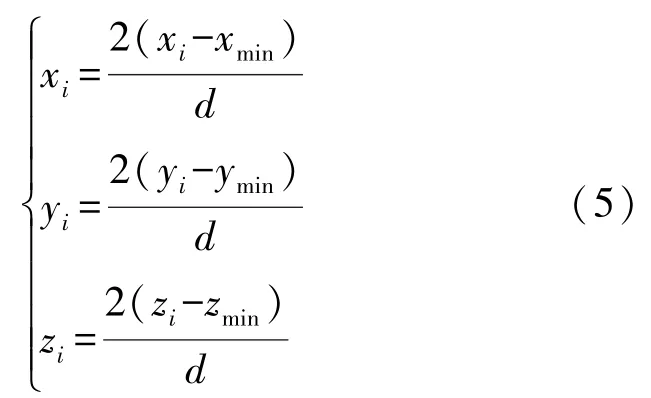
考虑计算显著度，首先需要确定网格顶点的领域灰度。设N(v，σ)代表的是半径为σ的顶点对应的邻域；gray(v)代表的是顶点对应的灰度值，采用欧式距离定义顶点对应的邻域:

式中:x代表的是网格中存在的点。

设G[gray(v)，σ]代表的是顶点灰度对应的高斯加权平均灰度值，可通过下式计算得到:

式(7)实际上为高斯滤波器，半径为2σ。

通过半径不同的灰度插值对网格显著度S(v)进行计算:

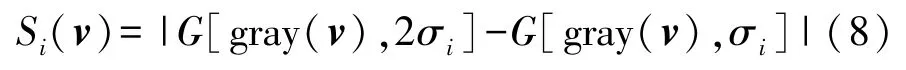
式中:σi代表的是高斯滤波在规格i下的标准差。

在相邻三角面的二次误差测度的总和可以视为，各网格顶点的颜色二次误差测度Q vc[9]，即:

当折叠边(v i，v j)到顶点时，颜色的二次误差测度Q c计算方式为:

设E g代表的是几何属性在折叠操作过程中对应的误差；E c代表的是颜色属性在折叠操作过程中对应的误差。考虑显著度S(v)，利用规范化函数w进行处理，使其规范到[1，Wmax]，对边折叠的折叠代价可通过下式计算得到:

选择堆中最小代价的边实施折叠操作，对相关信息进行更新，重复边折叠操作，当堆为空或达到简化要求后停止，实现网格模型的简化，获得简化后的网格模型[10-11]。

2 测距误差自动修复

测距结果中通常存在一些测距信息，如果直接剔除测距异常值，会导致信息损失，采用基于Huber损失函数最小化的Kalman滤波方法实现测距误差的自动修复[12]。

Kaman滤波的测量方程和状态方程为:

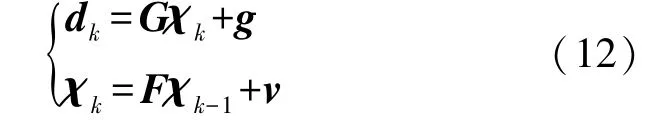
式中:d k代表的是量测值；G代表的是测量矩阵；χk、χk-1分别代表的是第k次和第k-1次的测距状态真实值；g代表的是量测噪声矢量；F代表的是状态转移矩阵；v代表的是系统噪声矢量。

设υ代表的是回归残差，最小化回归残差:

式中:ρ(υ)代表的是测距残差代价函数；ρl(υ)代表的是LOS测距结果对应的残差代价函数；ρn(υ)代表的是NLOS测距结果对应的残差代价函数。

针对回归残差代价，基于网络模型简化算法的测距误差自动修复方法采用Huber残差代价函数[13]进行定义:

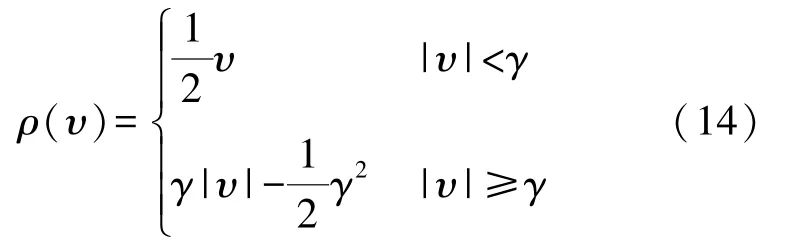
式中:γ代表的是阈值调节因子。

其中测距回归残差与阈值调节因子γ的关系应为:

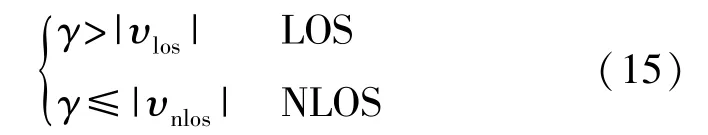
式中:υlos代表的是LOS对应的测距回归残差；υnlos代表的是NLOS对应的测距回归残差。

采用Huber回归方法修复测距误差[14-15]:

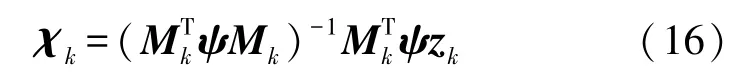
式中:ψ代表的是对角矩阵；M k、z k均代表的是过程参数。

3 仿真分析

为了所提方法的整体有效性，需要对所提方法进行测试，本次测试的开发环境为Visual Studio 2010。分别采用本文方法、文献[3]方法、文献[4]方法和文献[5]方法进行测试，对测距误差进行修复之前需要对测距误差进行检测，将测距误差检测概率作为测试指标对不同方法进行测试，测试结果如图1所示。

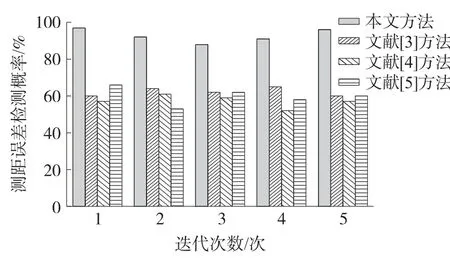
图1 测距误差检测概率测试结果

分析图1中的数据可知，在多次实验过程中本文方法的检测误差概率均在80%以上，表明本文方法在测距误差修复过程中可以较为全面地检测测距误差，文献[3]方法、文献[4]方法和文献[5]方法在多次实验中的测距误差检测概率均在60%附近波动，表明其他方法有很大概率无法检测出测距误差，影响后续的测距误差修复工作。对比不同方法的测试结果可知，本文方法的测距误差检测概率较高，因为本文方法采用网格模型简化算法对网格模型进行了简化处理，获得了结构简单的网格模型，可准确地获得相关信息和数据，提高了测距误差检测概率。

采用不同方法对测距误差进行修复，对比不同方法修复所用的时间，测试结果如图2所示。

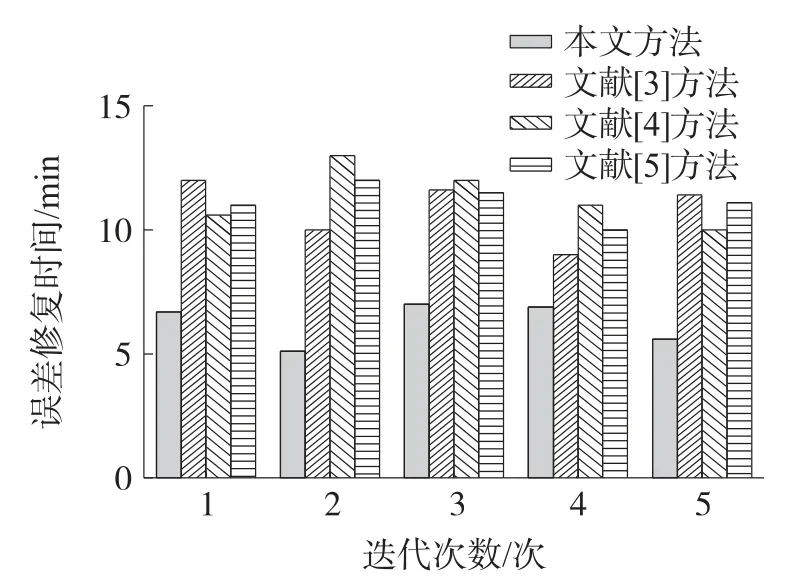
图2 误差修复时间测试结果

分析图2可知，对测距误差进行修复时，本文方法所用的修复时间平均为6.26 min，文献[3]方法、文献[4]方法和文献[5]方法所用的修复时间远远高于本文方法所用的修复时间，平均都在10 min以上。因为本文方法在简化网格模型的过程中保持了空间属性信息和空间位置信息的平等，并规范了网格属性坐标，可在较短的时间内完成网格模型的简化，进而提高了效率。

检测测距误差修复方法的重要指标之一是修复精度，分别采用不同方法进行测试，测试结果如图3所示。

由图3可知，本文方法修复测距误差的精度平均为80.6%，远远高于文献[3]方法、文献[4]方法和文献[5]方法修复测距误差的精度，均在55%左右。因为本文方法通过网格模型获取相关数据和信息，根据获取的数据和信息采用Kalman滤波方法在网格模型的基础上Huber平滑处理测距结果，通过采用Huber回归方法对测距误差进行修复，提高了测距误差修复的精度。

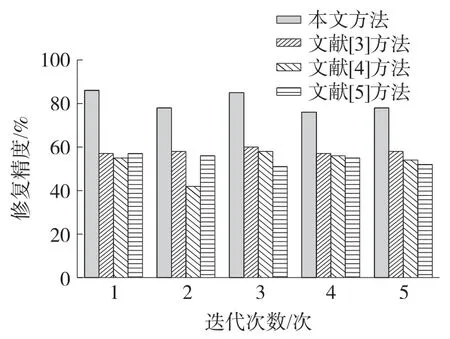
图3 修复精度测试结果

4 结束语

目前测距误差自动修复方法存在测距误差检测概率低、修复效率低和修复精度低的问题，提出基于网格模型简化算法的多传感测距误差自动修复方法，对网格模型进行简化处理，获得测距相关的数据和信息，利用Huber回归方法在网格模型的基础上实现测距误差的自动修复。经过仿真实验可以验证，本文设计方法能够通过网格模型，平均在6.26 min内获得相关信息，测距误差的自动修复精度高达80.6%，且误差检测概率达到80%。由于条件所限，本文研究的多传感器误差修复方法仅在仿真平台上应用，在未来的研究中，考虑应用于实际环境，并根据实际环境参数进一步改进，以期为高精度测量技术的发展提供一定的帮助。