地下道路结构配筋设计探讨

顾志超

（上海市政交通设计研究院有限公司，上海市200030）

0 引 言

随着国民经济和社会的发展，城市人口日趋集中，城市路面交通系统日趋紧张，开发地下空间资源、修建地下道路成为各大城市改善交通环境的一个发展趋势[1]。

城市地下道路结构，根据施工工艺可以分为明挖地道和暗挖地道。其中，明挖地道一般为闭合框架结构形式，根据车道规模又可以分为单孔框架、双孔框架等。

由于荷载、土体性质等因素变化较大，且缺乏统一的三维计算软件，设计人员对地下结构设计较民用建筑保守。对于相似的地下结构，不同设计人员的设计含钢量相差较大[2]。

在已有研究的基础上，针对明挖地下道路结构，从刚域、削峰、腋角、轴力、结构空腔等方面进行结构配筋设计探讨，以期为实际工程设计提供参考。

1 计算理论及模型建立

1.1 计算理论

（1）地道主体框架结构的受力分析一般可简化为平面问题，采用荷载结构法进行分析。

（2）地道底板厚跨比一般均小于1/6，宜按弹性地基理论计算内力[3]。

（3）荷载主要有永久荷载、可变荷载和偶然荷载。永久荷载分为结构自重、土层压力、水压力等；可变荷载分为地面超载、车辆荷载等；偶然荷载分为地震荷载、人防荷载等。

（4）地道结构配筋按裂缝控制。

1.2 模型建立

西安地区某地下道路工程双向六车道标准断面如图1所示，结构单孔净宽12.9 m，净高5.6 m，结构顶底板厚度1 m，侧壁厚度0.9 m，中隔墙厚度0.7 m，结构覆土厚度5 m，不考虑地下水位影响，地基基床系数为30 000 kN/m3，地面超载取20 kPa，混凝土强度等级为C35。

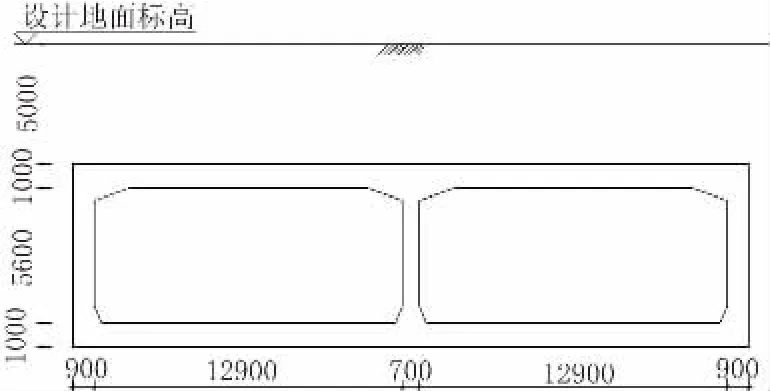
图1 地下道路结构横断面图（单位：mm）

采用Midas Gen结构有限元计算软件建立基本模型，按中轴线简化横断面计算，准永久组合弯矩图如图2所示。若采用此结果按裂缝配筋，支座计算钢筋需18 498 mm2，配筋率过大，易发生脆性破坏，且支座钢筋过密，难以施工。为此，需加大板厚，从而增加造价。

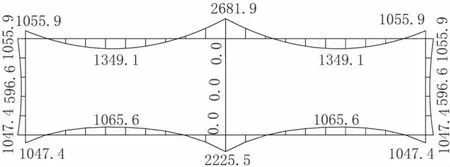
图2 基本模型准永久组合弯矩图（单位：kN·m）

2 内力取值及配筋优化

地道一般为宽扁型结构，顶底板跨度大于侧壁高度，最大弯矩值一般位于顶底板支座或跨中。同时，由于弹性地基变形协调作用，地道底板弯矩一般比顶板小。因此，现主要从顶板内力方面，研究刚域、削峰、腋角、轴力、结构空腔等对结构配筋的影响。

2.1 刚域

《混凝土结构设计规范》（GB 50010—2010）（2015年版）5.2.2条规定：梁、柱等杆件间连接部分的刚度远大于杆件中间截面的刚度时，在计算模型中可作为刚域处理[4]。

《高层建筑混凝土结构技术规程》（JGJ 3—2010）5.3.4条规定：在结构整体计算中，宜考虑框架或壁式框架梁、柱节点区的刚域影响。梁端截面弯矩可取刚域端截面的弯矩设计值。刚域的长度可按下列公式计算：

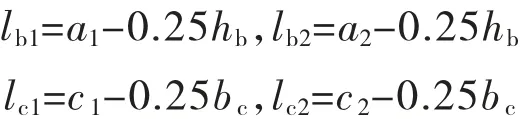
当计算的刚域长度为负值时，应取为零[5]。图3为刚域示意图。

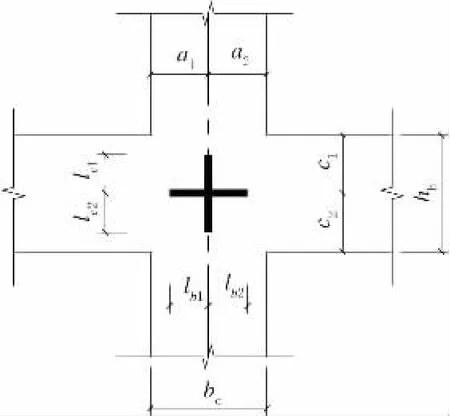
图3 刚域示意图

根据高层建筑混凝土结构技术规程取刚域长度，重新计算模型可得弯矩图如图4所示。考虑刚域后，顶板支座及跨中弯矩均减小约4%，可小幅减少配筋，但影响有限。

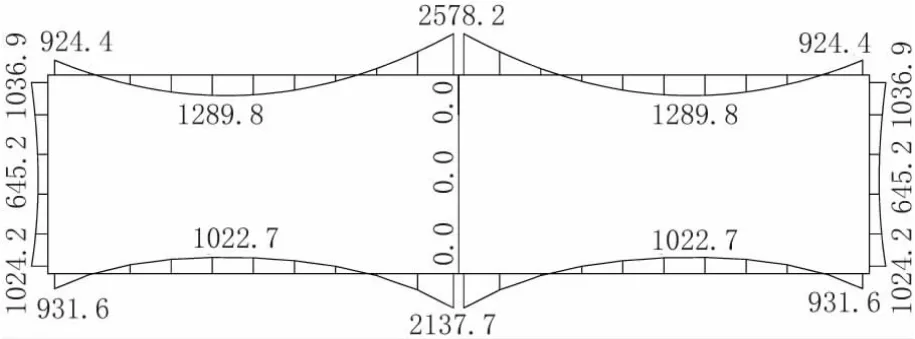
图4 考虑刚域模型准永久组合弯矩图（单位：kN·m）

2.2 削峰

无论是基本模型，还是考虑刚域模型，顶板支座弯矩取值位置均处于壁板范围内。但是，其并不是最不利截面。其最不利截面应是壁板边。根据上海市地方标准《城市轨道交通设计规范》（DG/TJ 08-109—2017）11.6.5条规定：纵梁截面配筋时，梁支座处的负弯矩可取柱边弯矩,按下列公式计算：

式中：M0为支座中轴线弯矩；Q0为支座中轴线剪力；b为支座宽度。

计算可得，顶板在中壁板边弯矩为2 438 kN·m，相比支座中轴线弯矩减少约9%，可减少支座配筋。

2.3 腋角

闭合框架结构增加腋角可有效改善角部应力集中现象，腋角最佳坡度比例为1∶3[6]。腋角的存在使得地道顶板在支座边缘的计算截面变大，对于配筋是有利的。但是腋角也增加了顶板支座处刚度，在矩形地道常用断面的加腋比的情况下,负弯矩可增加20 %以上[7]。

为分析腋角对于支座配筋的影响，在Midas Gen中建立地道1 m长断面的实体模型，顶板腋角高500 mm、宽1 500 mm，底板腋角高700 mm、宽300 mm。计算结果如图5、图6所示。顶板在中壁板边弯矩为2 595 kN·m，比平面框架模型弯矩大6.5%，但是截面高度可取1.5 m，计算配筋仅12 315 mm2，相比基本模型节约钢筋约33%。顶板跨中弯矩为1 114 kN·m，相比基本模型减少约17.5%。由此可见，考虑腋角作用可大幅优化顶板支座及跨中纵向受力钢筋。

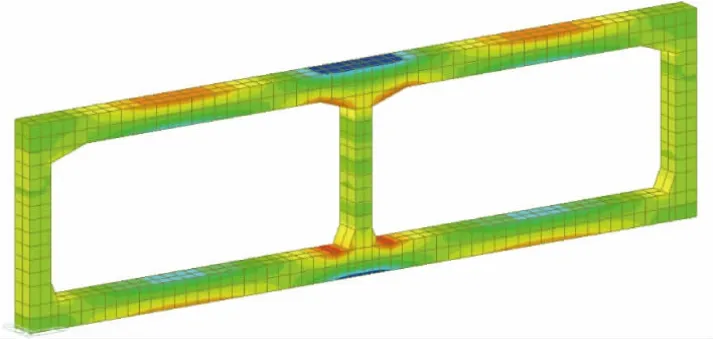
图5 实体模型准永久组合应力云图

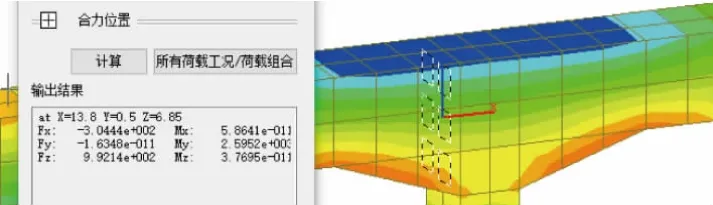
图6 实体模型顶板支座处准永久组合弯矩值云图（单位：kN·m）

增加腋角对于截面抗剪也是有利的，地道结构跨度一般较大，在深覆土情况下，顶底板剪力对结构截面高度起控制作用。以上文基本模型为例，基本组合下顶板在中壁板边剪力为1 324 kN，按1 m板厚验算抗剪是不满足的。由于顶底板、侧壁不能像梁一样采用箍筋或弯起钢筋抗剪，拉结筋抗剪计算也缺乏规范支持，只能增加板厚。若考虑腋角作用，截面计算高度可取1.5 m，截面本身抗剪即可满足要求。考虑腋角作用其实也是削峰的一种方式，值得注意的是，腋角、削峰都不能和刚域同时使用。

2.4 轴力

地道平面闭合框架顶底板和侧壁均为压弯构件，轴力对结构受力是有利的。以上文基本模型为例，顶板轴力来源为侧壁承受的侧向水土压力，侧壁高度相对较小，且地道暗埋段侧向水土压力一般为静止土压力，使得传至顶板的轴力较小，准永久组合工况下顶板轴力为263 kN，按压弯构件计算，配筋为17 693 mm2，配筋仅减小约4%。作为对比，取侧壁内力进行分析。基本模型侧壁支座弯矩为1 056 kN·m，轴力为955 kN，考虑轴力比不考虑轴力的配筋减小约25%，侧壁考虑轴力后可大幅减小配筋。

在实际情况中，地下水位不是一个定值，基坑围护桩对结构侧向土压力也有削减作用。结构分析计算时，侧向水压力一般按最高水位取值，顶底板的计算轴力一般是偏大的，应予以适当折减。侧壁承受的最大弯矩和轴力均由顶底板所受荷载确定，弯矩和轴力来源一致，规律一致，可按计算轴力考虑有利影响[2]。

2.5 结构空腔

地道结构内力主要由荷载及结构跨度决定，地道跨度受限于车道规模，难以减小。要减小结构内力，可从荷载方面入手。

地道顶板主要荷载为自重、覆土荷载、地面超载。对于深覆土地道而言，可通过在顶板上部增设结构空腔来减小覆土厚度，从而达到减小顶板荷载的目的。在地道方案设计时，应根据沿线城市规划，结合可共同实施的综合管廊、轨道交通、地下空间等市政基础设施，设置结构空腔。它既利用空腔空间、节约土地资源，又可减小工程造价。

以本文双向六车道地道为例，在顶板上增设净高2.5m的结构空腔，如图7所示。采用Midas Gen建立平面框架模型计算，准永久组合弯矩图如图8所示。

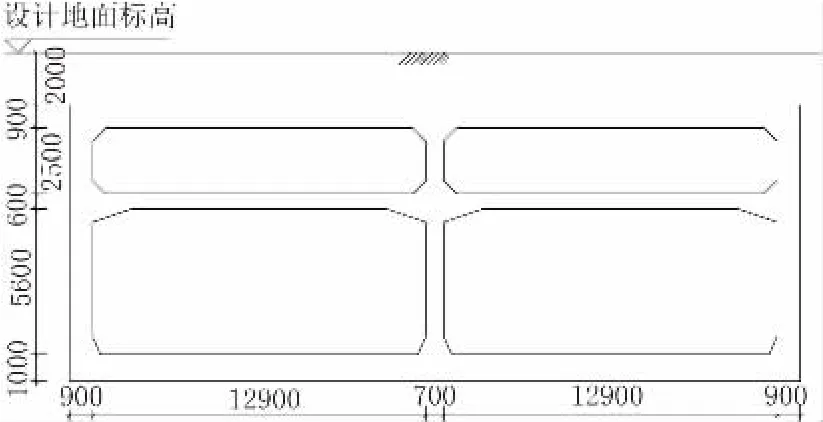
图7 地道增设结构空腔横断面图（单位：mm）

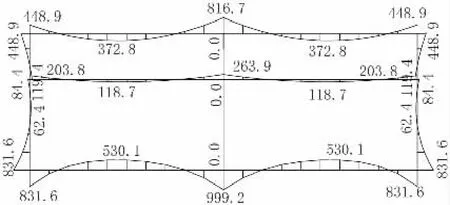
图8 增设结构空腔模型准永久组合弯矩图（单位：kN·m）

由图8可以看出，增设空腔后结构内力均大幅减小，顶板最大弯矩减小约70%，底板最大弯矩减小约55%。不考虑前文弯矩取值方式及轴力作用，仅以截面中轴线位置弯矩值计算顶底板及侧壁配筋，分别为6 158 mm2、6 283 mm2、5 686 mm2，配筋率分别仅为0.68%、0.63%、0.63%，结构壁厚还可适当优化。

2.6 结果总结

以地道顶板支座弯矩为例，将考虑刚域、削峰、腋角、轴力、结构空腔等模型计算结果与基本模型计算结果进行比较，结果见表1所列。

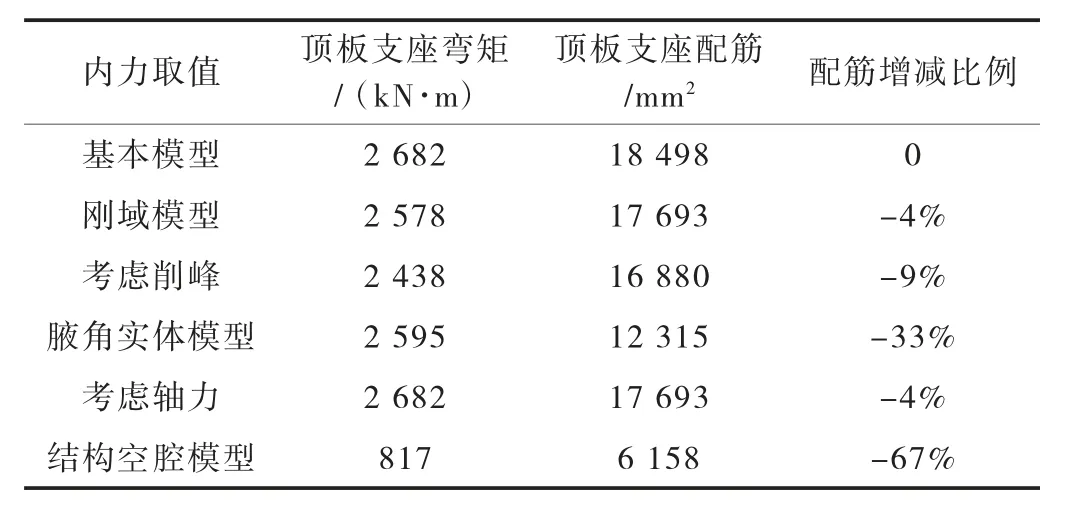
表1 计算结果对比表

3 结 论

本文在已有研究的基础上，针对明挖地下道路结构，从刚域、削峰、腋角、轴力、结构空腔等方面进行结构配筋设计探讨，得出以下主要结论：

（1）考虑刚域后，顶板支座及跨中弯矩均有所减小，但幅度不大，对配筋影响有限。

（2）考虑削峰后，顶板支座弯矩有所减小，可优化支座钢筋。

（3）考虑腋角后，顶板支座弯矩小幅增大，但配筋可大幅减少，跨中弯矩有所减小，配筋有所减少。

（4）考虑轴力后，顶板配筋减少有限，但侧壁钢筋可大幅减少。

（5）考虑结构空腔后，结构内力及配筋均大幅减小，结构壁厚也可适当优化。

根据上述结论，地下道路结构设计时，宜考虑腋角对结构内力及配筋的有利作用，大幅减少钢筋用量及造价。当地道覆土较厚时，应结合周边市政基础设施增设结构空腔，节约地下空间资源，大幅减少工程造价。