土压平衡盾构滚动角纠正方法研究

刘映晶

(中天建设集团有限公司， 浙江 杭州 310000)

0 引言

在交通强国战略的驱动下，我国城市轨道交通快速发展。截至2020年底，中国内地45座城市累计开通城轨交通运营线路总长7 978.19 km，其中，地铁线路总长6 302.79 km，占比79%[1]。在地铁施工中，盾构技术具有智能、安全、快捷等优点，逐渐成为地铁隧道建设的重要工法之一。

受地层不均匀性、曲线段掘进和盾构设备等影响，极易引起盾构反转矩不平衡，导致盾构滚动角变化[2]。近年来，国内外学者对盾构掘进纠偏技术进行了深入研究。郭玉海等[3]对土压平衡盾构反转矩进行理论分析和计算，对盾构正常掘进模式下阻滞力矩的构成和作用进行了分析。梁荣柱等[4]综合考虑覆土、盾构自重等多因素产生的阻滞力矩，提出在软土地层中盾构施工反转矩理论计算方法。刘成等[5]基于温克尔地基模型，推导出纠偏力矩与最小纠偏曲线半径的关系式，并提出优化后的水平线形纠偏曲线模型。高翔[6]通过ABAQUS有限元软件，建立考虑浆液注入的二维流固耦合模型，对盾构隧道竖向纠偏规律进行了研究。张爱军[7]通过BP神经网络得出施工参数与盾构姿态的关系，进而对盾构纠偏进行了研究。李洋[8]通过改进人工蜂群算法优化盾构纠偏模型，实现了地铁隧道建设中盾构的准确纠偏。Wang等[9]基于盾构掘进过程中数据驱动，提出一种轴线姿态偏差预测及修正方法，并验证了该方法的准确性。朱俊阳[10]通过理论分析和现场实测，推导出一种淤泥质土中纠正盾构滚动角施工所需千斤顶数量的计算公式，并对纠正措施和效果进行了分析。周洁[11]从盾体重心位置、地层原因等方面对滚动角偏转情况进行分析，采用辅助工装和定位油缸进行滚动角纠偏，并稳定了盾构姿态。李顺旭等[12]介绍了盾构在淤泥、淤泥质土地层掘进时的滚动角纠正方法。Shen等[13-14]分析了双圆盾构施工中出现滚动角偏转的原因，并给出合理可行的纠偏方法；此外，还通过有限元分析法分析了纠偏荷载、滚动角和土体变形之间的关系，以及纠偏过程中衬砌内力的变化特点。

目前针对盾构掘进姿态纠偏的研究较多，但对盾构滚动角纠偏的专门研究较少。基于此，本文结合杭州地铁7号线盾构隧道工程，建立了盾构掘进过程中的转矩计算公式。在此基础上，提出采用钢楔机构装置纠正盾构滚动角，给出相应参数的计算方法，并结合实际工程对纠偏方法进行验证。最后研究了隧道埋深、地层类型和盾构直径等参数对钢楔机构数量的影响规律。以期研究结果为盾构掘进期间滚动角的控制和调整提供参考和依据。

1 工程概况

杭州地铁7号线城站站—四季青站区间盾构隧道平均埋深15 m，主要穿越砂质粉土、淤泥质粉质黏土夹粉土、粉砂、黏土、粉砂夹砂质粉土和粉质黏土等土层，如图1所示，土体参数见表1。

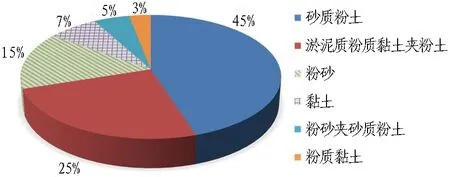
图1 隧道穿越土层地质统计图

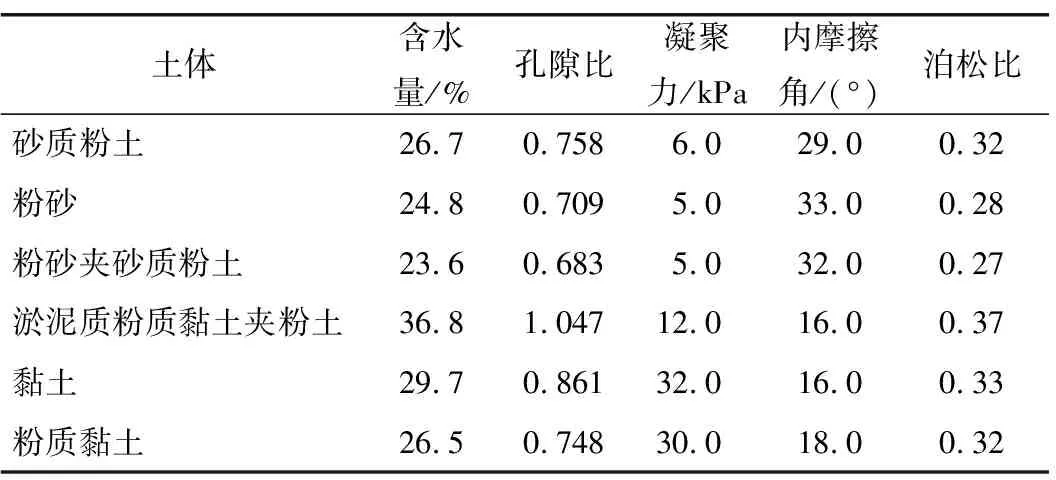
表1 土体参数

城站站—四季青站区间盾构隧道由于地质、线路等因素综合导致施工难度较大，具体如下：

1)地层是以砂质粉土和淤泥质黏土夹粉土为主的软土地层，表现较强的硬塑性，与盾构壳体之间的摩擦力较小，刀盘旋转使周围土体不能给盾构提供足够的反转矩。

2)隧道轴线走向转弯较多，且转弯半径偏小。在弯曲隧道掘进时，需要调整4个分区的压力差形成纠偏转矩，以调整盾构的方向； 但这也易导致盾构产生较大的滚动角。

3)土压平衡式盾构自身存在不足。当盾构重心出现偏转时，会产生偏转转矩，致使盾构在前进过程中滚动角变大。

2 盾构掘进中的反转矩

掘进过程中盾构的反转矩包括： 周边土层给盾构的阻滞力矩MZ，盾构自重及管片自重产生的阻滞力矩MG，以及掘进过程中千斤顶垫板与管片之间的摩擦力矩MQ[4]。盾构掘进中这些反转矩共同抵制刀盘切削岩土体带来的转矩MD，盾构掘进力学模型见图2。本文假定盾构穿越地层为单一土层，且不考虑地下水的影响，涉及多种地层的情况可参照计算方法进行推广应用。

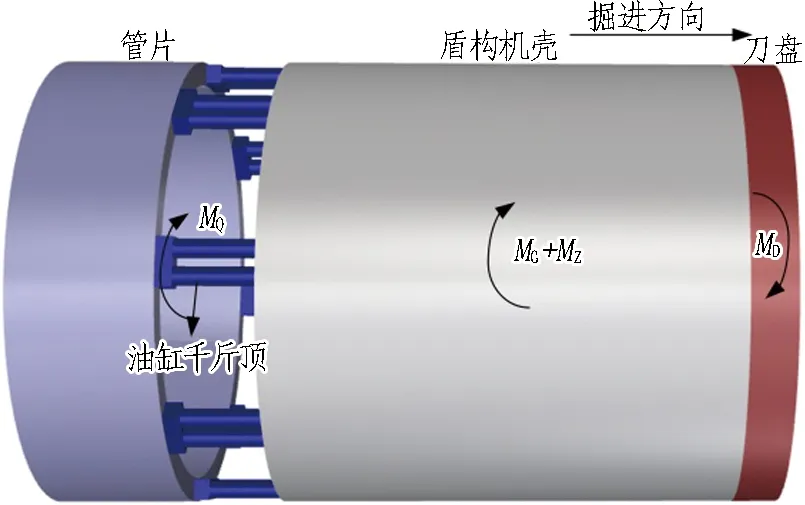
图2 盾构掘进力学模型

2.1 覆土产生的力矩

(1)

式中：μ0为盾构壳体与周围土体间的阻滞摩擦因数;γ为土的重度，kN/m3；H为盾构上考察点距地表的深度，m；l和R分别为盾构壳体长度和半径，m；θ为盾构偏转产生的滚动角。

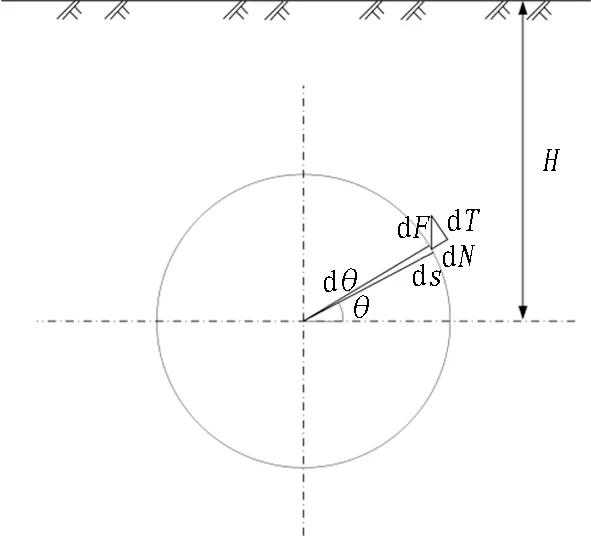
图3 盾构壳体表面受力图

2.2 盾构和管片自重产生的反力矩

当盾构在掘进过程中，若盾构壳体发生转动或有发生转动的趋势，盾构自重同样会产生阻滞力矩；同时，盾构内未脱节安装的管片自重也会产生一定的阻滞力矩。力矩大小为：

MG=(G1+nLG2)μ0RL。

(2)

式中：G1为盾构主机自重，kN；G2为盾构内管片自重，kN；nL为管片的个数；RL为盾构管片中心线到隧道轴线的距离，m。

2.3 千斤顶产生的力矩

在盾构掘进过程中，管片固定不动，推进油缸通过撑靴施加顶进推力作用在管片上。当盾构在推进过程中机体出现回转或者有回转趋势时，推进油缸上撑靴在管片上会产生摩擦力，摩擦力产生的反力矩会阻滞盾构滚动角的产生，其计算公式为：

(3)

式中：μ1为推进油缸撑靴与盾构管片的静摩擦因数；Fi为第i个推进油缸的推力，kN；Rp为推进油缸轴线到盾构轴线的距离，m。

2.4 施工盾构的反转矩

将式(1)—(3)进行叠加，可得到施工盾构的反转矩：

M=MZ+MG+MQ。

(4)

为保证盾构在掘进过程中不会产生回转角，盾构刀盘转矩MD不能大于盾构反转矩M，即：

M≥MD。

(5)

式中MD=kD3(D为刀盘直径；k为取决于地层条件和盾构类型的系数，对土压平衡盾构，k=8～23[15])。

3 盾构纠偏方法研究

3.1 传统纠偏方法

当盾构在掘进中产生轻微滚动时，反向回转刀盘一般都可复位；但当盾构滚动角较大时，按照传统方法，需清空土舱内土体，然后在盾构的适当位置悬挂一定的重物，通过改变盾构重心位置使回转角自行缓慢纠正。但该方法悬挂物数量具有不确定性，且悬挂重物影响施工进程，造成工期延长，其纠正效果一般。基于此，朱俊阳[10]发明了一种改变盾构滚动角的千斤顶钢板装置，如图4所示。

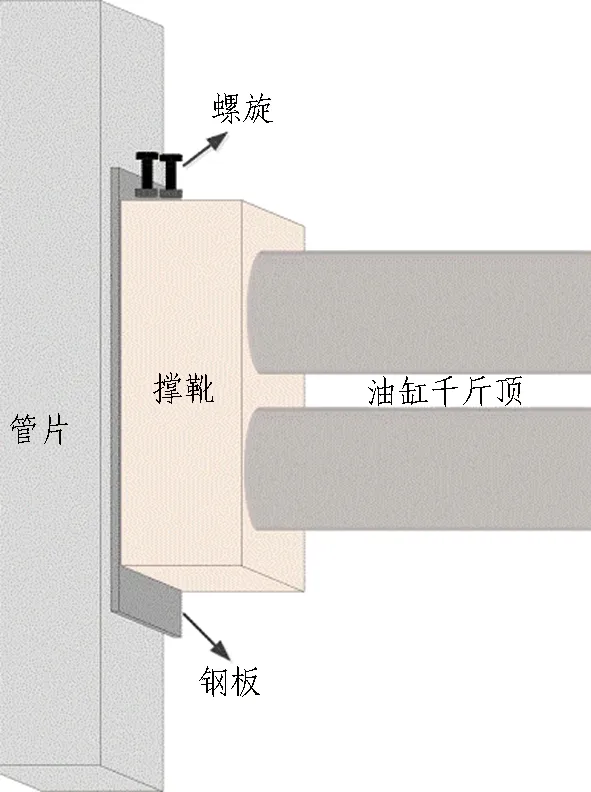
图4 千斤顶钢板装置示意图

但该装置在实际应用中仍存在不足：

1)螺旋拧进深度与推力的大小关系不明确，操作时完全凭借经验来调整；

2)在盾构推进过程中，撑靴与螺旋的接触稍有脱离，千斤顶推力就会消失，需要实时拧进螺旋，操作繁琐；

3)千斤顶钢板的螺旋拧至最底后需要停止盾构掘进，调整千斤顶钢板的位置，并将螺旋拧至最顶端，造成盾构效率降低，影响工期。

3.2 钢楔机构纠偏方法

在盾构反转矩分析的基础上，结合朱俊阳[10]提出的纠偏方法，本文提出一种钢楔机构来纠正盾构的回转角，其装置纠偏原理如图5所示。

推进油缸的推力p0作用在钢楔机构上，由于角度α的存在，在撑靴上会产生一个分力p0sinα，为克服钢楔机构与撑靴之间的摩擦力f而形成对油缸的环向转矩，1个推进油缸能提供的纠偏环向力矩：

(6)

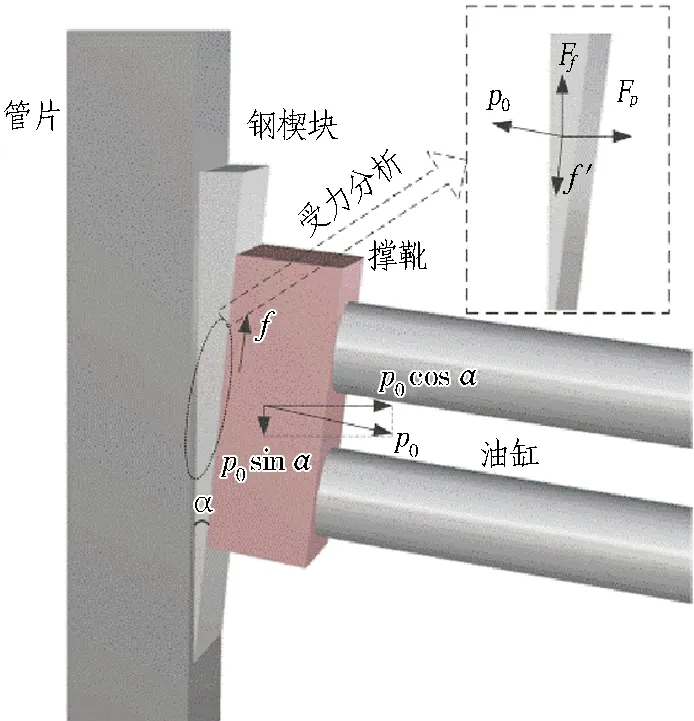
图5 钢楔机构纠偏原理图

为保证盾构能稳定纠偏，即钢楔机构在管片上不发生滑动，钢楔机构的角度需满足：

(7)

根据式(7)，可以设计具有一定角度的钢楔机构，将钢楔机构布置在推进油缸的撑靴与管片之间，单个钢楔机构在双油缸推力下产生的纠偏力矩为T0。图6为盾构滚动角纠正模型图，需要根据式(8)确定钢楔机构的数量n，以达到纠正盾构滚动角的效果。

nT0+MD>MG+MZ。

(8)

图6 盾构滚动角纠正模型

3.3 现场验证

表2 盾构穿越土层力学参数

表3 土压平衡式盾构主要性能参数

由上述分析结果，本工程的钢楔机构采用角度约为7.6°的三角钢板，材质为Q235，钢楔机构模型如图7所示。

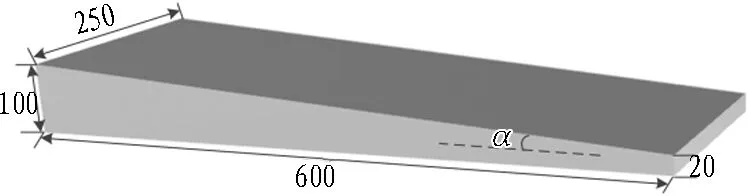
图7 钢楔机构模型(单位： mm)

将现场相关数据代入式(8)，可以求出n≥7.7。因此纠偏现场选择安装8块钢楔机构，如图8所示。

图8 钢楔机构现场安装图

盾构滚动角监测数据见图9。由图9可知，在左线掘进至第390环时，盾构滚动角增大，滚动角为10 mm/m。随后及时反转刀盘，由于刀盘反转转矩达不到盾构的纠偏转矩，滚动角仍然持续增大。当掘进至第447环时，滚动角达到100 mm/m。随即采用钢板千斤顶纠正方案掘进3环后，滚动角降低5 mm/m；但到第450环后，滚动角又开始增大。究其原因，主要是螺旋千斤顶与撑靴容易脱离，不能持续提供纠偏力。在第460环，滚动角为116 mm/m时，采用本文中的钢楔机构纠正方案，采用8块角度为7.6°的钢楔机构，布置在盾构中下方油缸位置，对称分布。纠偏后，盾构滚动角迅速减小；在掘进到第490环时滚动角降低到4 mm/m，在控制范围内，盾构能正常掘进。由此说明钢楔机构方案可以迅速、有效地纠正盾构滚动角。

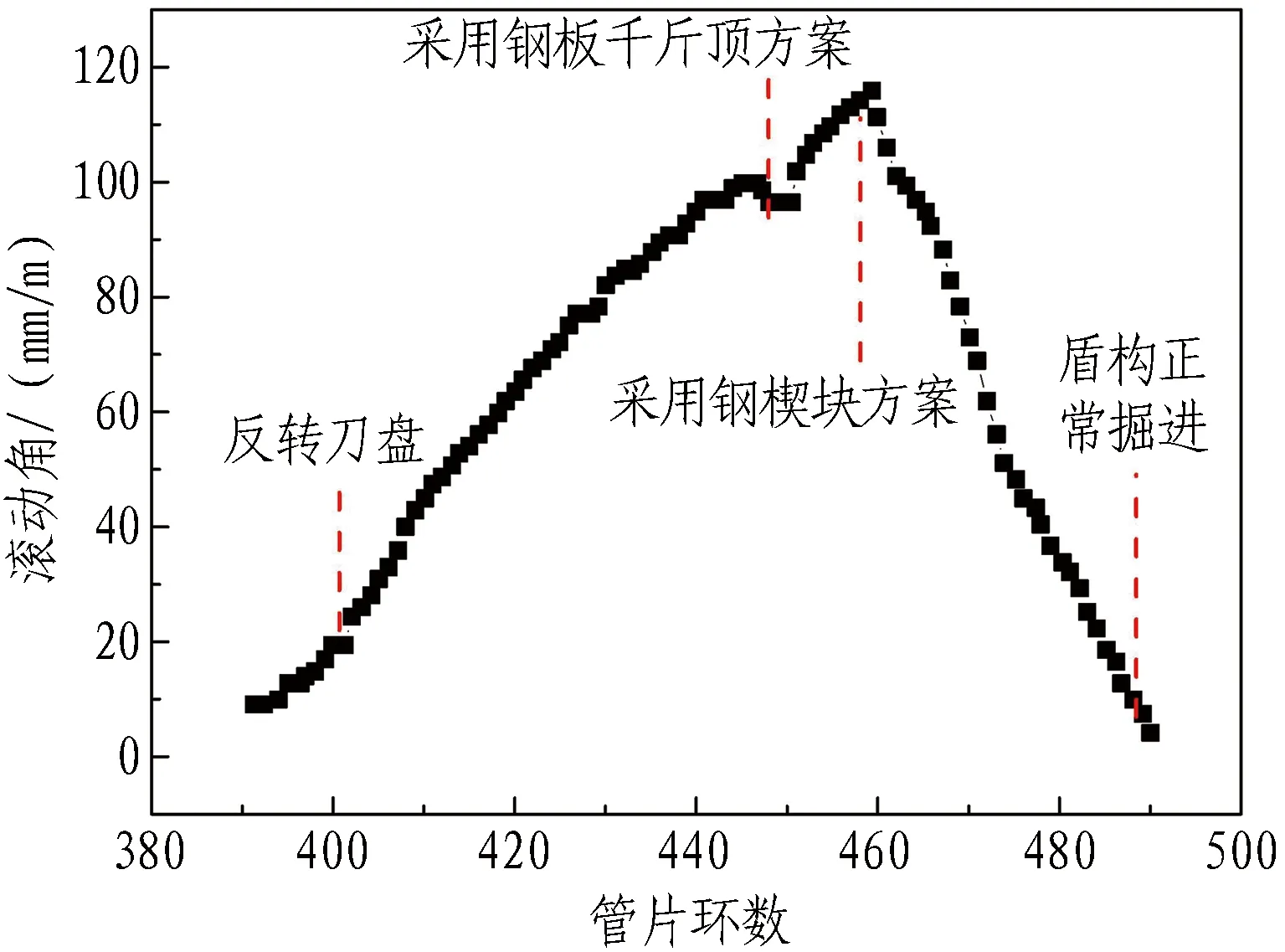
图9 盾构滚动角监测数据

4 钢楔机构数量的影响参数分析

4.1 盾构隧道埋深

通过单一变量控制法保证其他参数不变，研究隧道埋深对钢楔机构数量的影响规律，根据式(8)，假定其他参数为定值，均按照本项目实际工况选取，可以推导出钢楔机构数量与隧道埋深的关系式为：

n≥2.18H-14.03。

(9)

图10为钢楔机构数量与隧道埋深的关系图。由图可知，当其他变量保持不变时，钢楔机构数量与隧道埋深成线性正相关，埋深每增加1 m，钢楔机构数量增加约2块。

图10 钢楔机构数量与隧道埋深的关系

4.2 盾构隧道地层类型

在保证其他参数不变的前提下，研究地层类型与钢楔机构数量的关系。根据式(8)，可以推导出钢楔机构数量与地层条件的关系式为：

n≥-0.87k+17.81。

(10)

式中k为与地层条件和盾构类型相关的系数。

图11示出了钢楔机构数量与土压平衡盾构地层条件相关系数的关系。由图11可知，当其他变量保持不变时，钢楔机构数量与地层条件和盾构类型相关的系数k成反比，k每增加1，钢楔机构数量减少约1块；且对于土压平衡盾构，k=8～23，所以在其他参数不变时，地层类型改变，钢楔机构数量变化为1～11块。

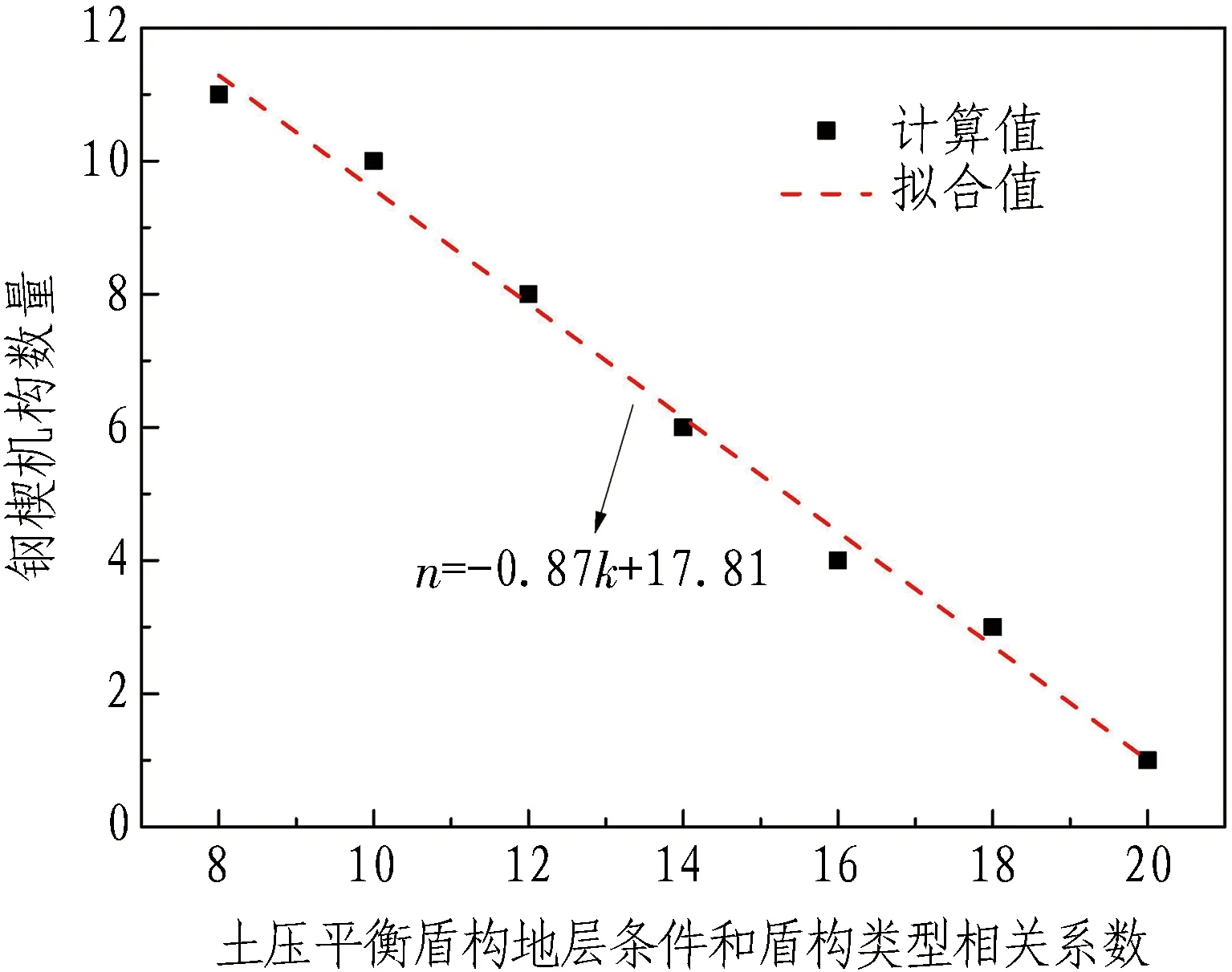
图11 钢楔机构数量与地层条件的关系

4.3 盾构直径

在其他参数保持不变的前提下，研究盾构直径对钢楔机构数量的影响规律，根据式(8)，可以推导出钢楔机构数量与盾构半径的关系公式为：

n≥2.13R2-0.52R3+0.94R。

(11)

图12为钢楔机构数量与盾构半径的关系图。由图可知，当其他参数保持不变时，钢楔机构数量与盾构半径成三次函数关系，且随着盾构直径的增加，钢楔机构数量先增大后减小。

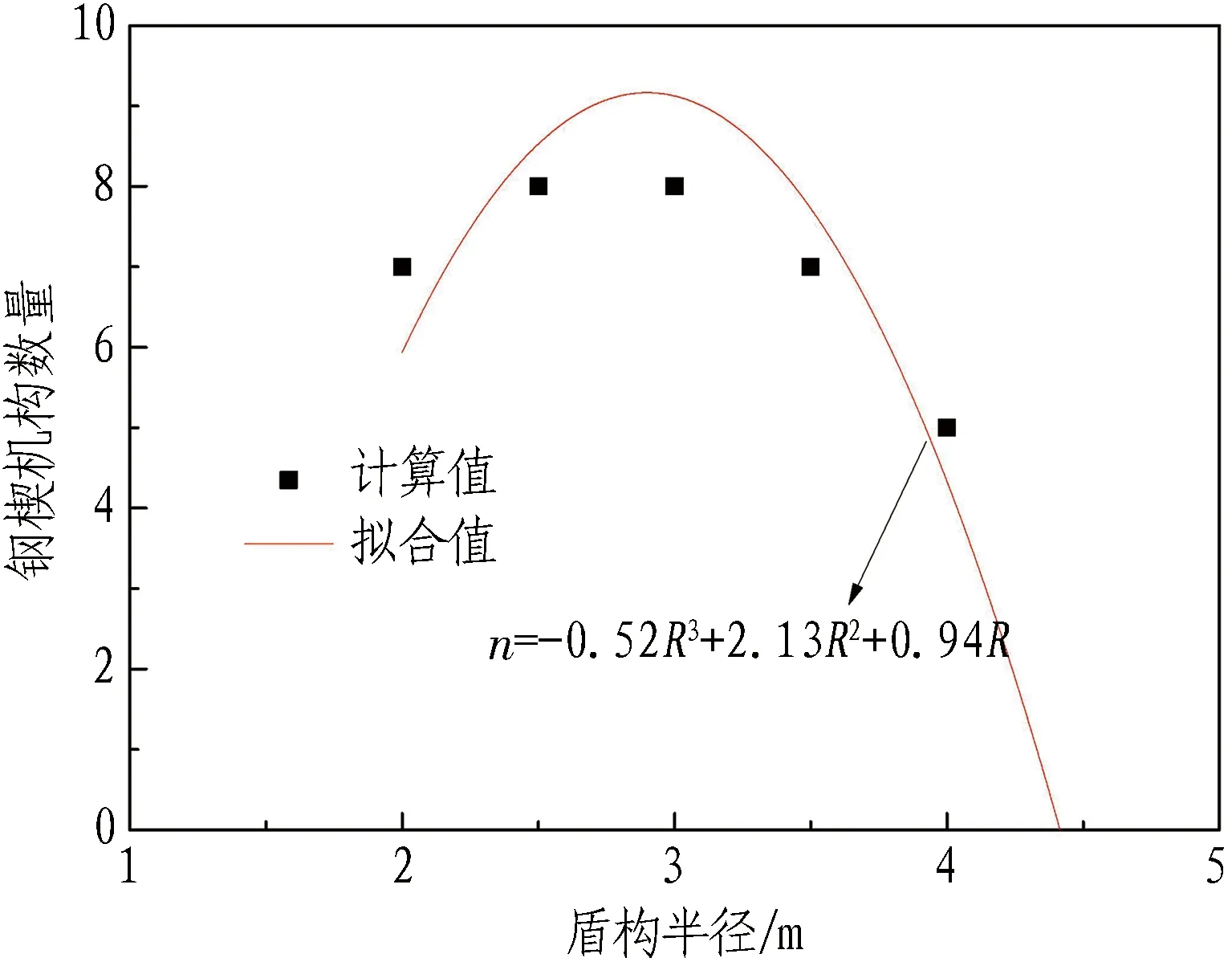
图12 钢楔机构数量与盾构半径的关系

5 结论与讨论

本文提出了一种土压平衡盾构的新型滚动角纠偏施工技术，建立了转矩和使用数量的计算公式，并对影响参数进行了分析，得出以下结论：

1)根据土压平衡盾构掘进中所受力矩的分析，建立了盾构反转矩计算公式，得出了反转矩与刀盘转矩间的关系。

2)提出了一种钢楔机构装置，用以纠偏盾构滚动角；基于建立的转矩计算公式，推导出了钢楔机构对应的力矩及使用数量的计算公式；并结合杭州地铁7号线工程验证了钢楔机构纠偏装置的可行性。

3)钢楔机构数量与隧道埋深成线性正相关、与地层条件系数成线性负相关，与盾构直径成非线性三次函数关系。

在进行土压平衡盾构滚动角纠偏时，应结合实际地层情况、盾构埋深、盾构尺寸及现场可实施条件等进行综合判断，选择合适方法，才能取得较好的效果。