考虑合理缓冲的PPP轨道交通项目弹性特许期研究

易 欣， 邱凯洁， 张跃斌， 沈良峰

(中南林业科技大学土木工程学院， 湖南 长沙 410004)

0 引言

轨道交通项目投资大、技术复杂、不确定性高，为了减轻财政压力和提高运营效率，PPP(public private-partnership)模式正被广泛运用于该领域。PPP轨道交通项目特许期是政府和社会资本特许协议谈判的核心内容之一。过短的特许期可能使项目公司无法收回投资和获得期望收益，甚至导致项目失败； 而过长的特许期则可能使其获得超额利润而损害公共利益。因此，确定特许期是否合理对PPP轨道交通项目能否成功至关重要。

一方面，轨道交通项目的建设和运营涉及专业众多，且客流量预测难以做到足够精确；另一方面，PPP项目本身运作流程复杂，因此特许协议不可能覆盖未来所有情况，导致了事实上的契约不完全。这些都给PPP轨道交通项目特许期的“精准”决策带来了困难。依据特许协议约定，PPP项目分为固定和弹性特许期2类。固定特许期有明确的唯一特许时间，除非特殊原因否则不能调整。实践中，由于准确预测项目收益的困难性，期初不合理的固定特许期设定，既可能因项目收益过高而影响社会公平，也可能因缺乏调整空间而导致项目失败。而弹性特许期不直接规定特许时间，以现金流量达到约定界限为准[1]，不仅有利于风险分担,而且争议更小。它能通过特许期的调整有效降低社会资本攫取超额利润的风险，也能成为激励社会资本努力提高运营绩效的有效工具，已成为特许期研究的主要方向。

目前弹性特许期领域应用最广的是净现值(NPV)法，以及在此基础上扩展出的最小收入现值(LPVR)等模型[2]。此外，蒙特卡洛模拟、系统动力学和灰系统等也常被用于弹性特许期的预测[3]；还有学者重点考虑了项目收益预测的误差，提出了特许期与价格联合调整的模型[4]。程敏等[5]则将其视为较复杂PPP项目的一种更灵活的激励措施，从再谈判的信号博弈角度讨论了城市污水处理PPP项目的特许期调整。综上，有利于公私合理分担项目风险的弹性特许期，在运营收入预测困难的PPP项目得到了广泛应用，但现有成果多针对高速公路、污水处理等可运营获利的使用者付费项目。尽管PPP轨道交通项目与这些项目有相似之处，如投资规模大和周期较长等，但也有很大不同，它需要政府支持才能维持运营，属于可行性缺口补助项目。在实践中，可行性缺口补助项目所获政府支持必然与项目绩效密切相关，而现有成果多未考虑项目绩效对特许期的影响。鉴于此，本文将引入关键链理论(CCPM)设置缓冲区的思想[6]，既充分考虑各种不确定因素对特许期带来的影响，又将项目绩效表现与缓冲区的动态管理相结合，研究适应轨道交通项目实际需要的弹性特许期决策理论与方法，以促进PPP模式在轨道交通领域的成功。

1 基于合理缓冲的PPP轨道交通项目弹性特许期理论分析

CCPM通过设置缓冲区有效解决了项目进度受各种不确定因素影响的问题，通过缓冲机制来保护计划的稳定性[7]。缓冲区的设置和管理对于确保项目顺利完成和提高项目绩效都至关重要[8]，已在复杂环境下的高速公路项目进度管理[9]、航天型号项目柔性管理[10]等领域得到了有效应用。类似地，PPP轨道交通项目环境复杂，特许期也受诸多不确定性因素影响，故本文采取合理设置缓冲区的方式来确定弹性特许期，以有效应对这些不确定因素影响。其理论模型为：

T=TB+TI+TM。

(1)

式中：TB为基本运营期；TI为综合考虑各种不确定因素对特许期影响后设置的初始缓冲区；TM为缓冲区的动态调整值，根据社会资本的运营质量等绩效表现，通过奖惩机制动态调整缓冲区大小(延长或缩短)，激励其发挥自身优势。

由式(1)可知，应首先确定PPP轨道交通项目的基本运营期。为了更准确地确定项目基本运营期数值，本文提出了耦合净现值和工程实际数据的测算方法，具体如下。

1.1 仅考虑项目净现值的基本运营期测算

令采用净现值法确定的项目基本运营期为TBc，

NPVmin≤NPV≤NPVmax。

(2)

式中： NPVmin表示项目刚好收回投资； NPVmax表示社会资本已获预期收益，此时应终止特许期；由此对应基本运营期的上下限TBcmin和TBcmax。

(3)

式中： CIt和COt分别为第t年的现金流入和流出；i为基准折现率；V为项目投资额的折现值；R为合理利润率。

1.2 仅考虑工程实际数据的基本运营期测算

令考虑实际操作需要的基本运营期为TBd。由于TBc只是从理论上算出的基本运营期，而在实际工作中往往还需要参考同类既有项目，故选取了财政部40个PPP轨道交通示范项目的特许期数据，并根据经济发展水平差异进行分类，具体如表1所示。

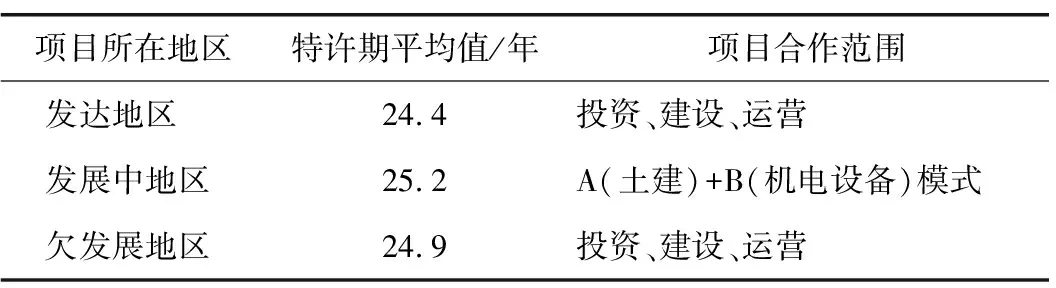
表1 财政部PPP轨道交通示范项目特许期

由表1可知，除合作范围有所不同外，各地区的特许期长度并无明显差异。这也一定程度上反映了各地政府为加快项目“落地”，在缺乏有效方法和依据支撑的情况下，实际操作中往往直接套用相同固定特许期的做法，忽视了不同项目的市场、环境等因素差异，可能给未来运营带来隐患，甚至导致再谈判后的特许期调整。

1.3 耦合净现值和工程实际数据的基本运营期测算

将上述两者综合考虑，故TBd为40个项目的特许期均值，最后将TBc和TBd有效耦合：

TBmin=μ1TBcmin+μ2TBd；

(4)

TBmax=μ1TBcmax+μ2TBd。

(5)

式(4)—(5)中：μ1、μ2为耦合系数，μ1+μ2=1(μ1>0，μ2>0)，为简便计算，假设2种方法重要性相同，则μ1、μ2均取0.5。

此外，由于网络效应可扩展轨道交通项目的客流量，根据轨道交通项目引入PPP的时机可分为网络形成前、形成时和形成后3个不同阶段[11]，故PPP轨道交通项目的基本运营期应根据引入时机在[TBmin,TBmax]合理取值，如表2所示。

表2 PPP轨道交通项目的基本运营期选取

2 PPP轨道交通项目弹性特许期的初始缓冲区设置

2.1 影响特许期的不确定因素识别及数据分析

Gusach[12]发现在价格和交通量等不确定因素影响下，交通类PPP项目大都在长时间再谈判后调整了特许期。因此，需要有效识别影响PPP轨道交通项目特许期的不确定因素。2020年8月，本文课题组依据相关研究成果并结合轨道交通行业特点，向参与过类似项目的政府部门、轨道交通公司、社会资本等进行问卷调查。本次调查采用Likert 5分量表表示影响程度，共发出问卷200份，回收有效问卷147份，满足样本量需要。最终，得到24个影响因素，通过SPSS25.0求得Cronbach′sα值为0.927，表明数据信度良好；KMO值为0.918，χ2值为2 563.950，显著性为0，说明适合进行因子分析；采用探索性因子分析法提取到6个公因子及相应权重，如表3所示。

表3 影响PPP轨道交通项目特许期的不确定因素权重

2.2 初始缓冲区设置的模型构建

缓冲区的设置可以综合度量各因素对特许期的影响。由于弹性特许期的长度由项目现金流量决定，故除专家打分给出的各因素对特许期影响主观权重外，还应考虑其对现金流量的客观影响程度，本文采用该因素的敏感性系数表示。同时，根据轨道交通运输特点可知，表3中部分因素对现金流量的影响程度并非始终不变，而是随运营阶段的不同发生动态变化。最后，依据缓冲区的建模思路[13]，构建PPP轨道交通项目弹性特许期的初始缓冲区模型：

(6)

式中：TBj×0.5是借鉴了经典的剪切粘贴法取50%安全时间设为缓冲区的思想，表示这些不确定因素可能发生变化并影响特许期的概率为50%；αi为第i个因素对特许期影响的主观权重(见表3)；βi为第i个因素的敏感性系数；γij为第i个因素对第j阶段的影响系数。

令ΔUi表示第i个因素的变化率，ΔNPVi表示此时NPV相应的变化率，则

(7)

《城市快速轨道交通工程项目建设标准》规定“项目设计年限分为初期、近期和远期，分别为建成通车后的第3、10和25年。”故在j=1,2,3时，TBj分别表示初期(0～3年)、近期(3～10年)及远期(10～TB年，TB由1.3节求得)，将与运营阶段有关的影响因素(见表4)分为3段计算并以γij表示。由于弹性特许期与现金流量密切相关，因此根据项目在不同运营阶段的年补贴金额比例关系1.03∶1.0∶1.41[14]，同时借鉴变权思想对γij赋值，γij越大则说明该因素在此阶段对特许期的影响程度越大，具体取值如表4所示。

表4 与运营阶段有关的影响因素γij取值表

对表4的解释是初期为了最大程度吸引客流，“乘客体验因子”及“沿线配置资源”等影响较大；近期客流量增速急剧，“地方人口数”、“技术水平”及“折返能力因子”能否跟上客流剧增的影响非常重要；而到了远期，运营成本随着项目规模增大而增加，此时“线路形式”、“车公里数”等因素的影响更为重要。除了这些因素之外，其他因素在非发生突发事件时对特许期的影响几乎不变，与运营所处阶段无关。

3 PPP轨道交通项目特许期的缓冲区动态管理

3.1 项目运营绩效影响因素的识别与数据分析

PPP轨道交通项目因引入社会资本而提高了项目运营效率，但如何能有效激励其持续改善运营绩效十分重要。因此，本文将项目特许期缓冲区的动态管理与社会资本运营的经济性、安全性和服务质量等绩效表现相结合，通过有效的奖惩机制动态控制缓冲区大小(延长或缩短)，以此激励社会资本提高运营效率。首先，根据城市轨道交通服务质量与满意度评价相关标准，采用问卷调查方式获得项目运营绩效评价指标体系，如表5所示。

表5 PPP轨道交通项目运营绩效指标体系及权重

3.2 基于项目运营绩效的缓冲区动态管理

根据前述分析，PPP轨道交通项目实际运营时需根据社会资本的运营绩效表现，对缓冲区进行相应地动态调整以更好激励其不断提高和改善运营效率。因此，进一步提出缓冲区动态调整系数BDAF(buffer dynamic adjustment factor)[15]，

TM=TI×BDAF。

(8)

BDAF的取值由项目特许期的运营绩效决定，设定相关规则如下：

(9)

式中：Emin、Emax分别为向量E中的最小值和最大值。

(10)

4)设定BDAF，

(11)

依据《城市轨道交通服务质量与满意度评价》对运营服务评价等级的规定，绩效考核评分在0.6以上即为合格。考虑到PPP轨道交通项目运营绩效应高于此标准，故选取传统项目代表优良等级的0.8作为PPP轨道交通项目运营合格的阈值，如式(11)所示。

4 实证研究

K市轨道交通5号线采用PPP模式，为贯穿主城东北到西南方向的辅助线路，全长24.6 km，设置车站21座(含换乘站5座)，根据前述思路对该项目的特许期长度进行测算。

4.1 基本运营期的测算

以可研报告中项目投资现金流量表的相关数据作为基本运营期计算依据，其中i为7.5%，R为3%，项目投资额为1 934 000万元，建设期流出共1 988 934万元，如表6所示。

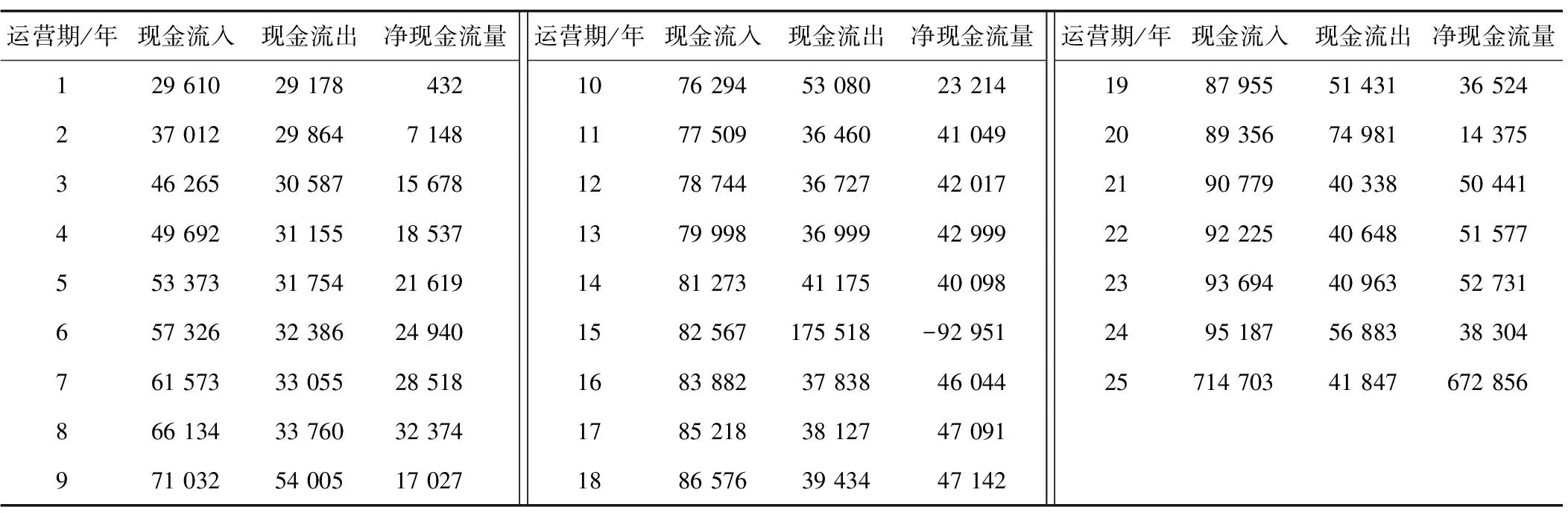
表6 K市轨道交通5号线运营期现金流量表

由式(3)可得：

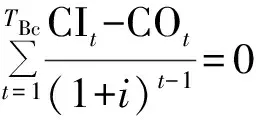
由式(4)和式(5)计算可得：

TBmin=19.33，TBmax=25.15，即19.33≤TB≤25.15。因项目建成后该城市的轨道交通网络将初步形成，故选取中间值TB=22.24≈23年。

4.2 初始缓冲区TI的测算

因可研报告仅提供了对客运量和投资额进行敏感性分析的相关数据，故将表3中所有因素分为影响客运量的因子U1、U2、U3和U5，以及影响投资额的因子U4和U62大类，然后进行敏感性分析，结果如表7所示。

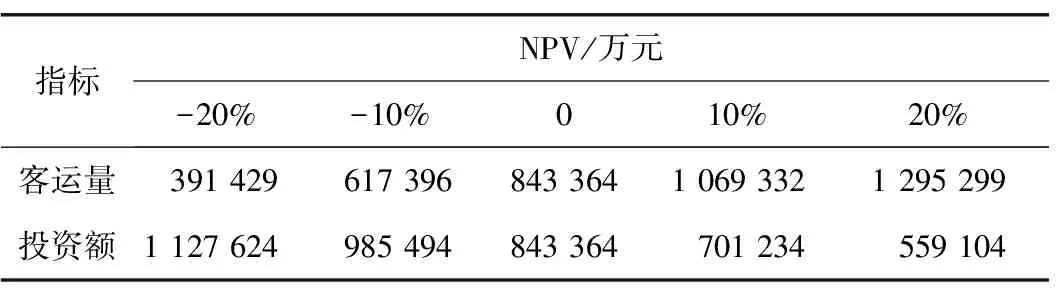
表7 K市轨道交通5号线影响因素的敏感性分析表

由表7及式(7)得：

标准化得：βU1=βU2=βU3=βU5=0.61，βU4=βU6=0.39。

再将γij代入TB，得TB1=2.67，TB2=6.23，TB3=13.34。

由式(6)和式(7)计算得

TI=0.5×(0.55TB1+0.51TB2+0.58TB3)=6.19，故TB+TI=28.43≈29年。

因此，考虑初始缓冲的项目特许期为29年，政府可以此为依据与社会资本进行谈判。

4.3 缓冲区动态管理TM的测算

由于该项目仍处于前期采购阶段，故此处的运营绩效及动态管理均为虚拟数据，仅为验证所需。假设项目运营一段时间后，邀请8位专家对该项目的绩效表现从因子K1至K7进行打分，结果如表8所示。

表8 K市轨道交通5号线的运营绩效评价表

由式(8)—(11)计算得：

E=(4.21,4.29,4.29,4.3,4.27,4.21,3.97,4.32)；

E′=(0.69,0.91,0.91,0.94,0.86,0.58,0.69,0，1.00)。

由上述计算结果可知：

1)根据可研报告相关数据，以及项目建成后该市的轨道交通网络形成情况，该项目的基本运营期应为23年，小于社会资本获得最大回报的25.46年，更好地维护了项目公共属性；

2)在综合考虑各种不确定因素对实际运营影响的基础上，当不确定性因素带来负偏差影响时，在公私合理分担风险的基础上该项目特许期可延迟至29年，这有利于提高项目应对未来运营风险的能力；

3)在首次绩效考核时，因社会资本绩效表现低于该项目设定的绩效考核目标值，故社会资本应受到惩罚，特许期调整为27年。

同理，若下一次考核时，社会资本经过努力后绩效表现超出了设定标准，则同样可获得相应的缓冲区延长奖励。因此，通过定期地动态考核，可以有效激励社会资本改善项目绩效表现，付出其应有的努力程度和兑现真实的资源禀赋，从而持续改进运营管理，使公私双方获得双赢，推动我国 PPP 轨道交通事业的健康发展。

5 结论与建议

本文将关键链理论应用于PPP轨道交通项目的弹性特许期分析，通过合理的初始缓冲区设置与后续动态管理，弥补了以往研究成果无法有效应对不确定因素影响以及激励社会资本的不足，并根据K市轨道交通5号线项目进行了实证研究，得出以下结论：

1)根据耦合净现值法和工程实际数据测算了项目基本运营期，考虑各种不确定因素影响设置了项目的初始缓冲区，依据项目运营绩效给出了缓冲区动态调整系数及其评判阈值，在此基础上构建了考虑合理缓冲的PPP轨道交通项目弹性特许期模型。

2)通过问卷调查识别出影响PPP轨道交通项目特许期的24个不确定因素，采用探索性因子分析法聚类后得到6个公因子及其对特许期影响的相应权重。

3)遵循《轨道交通服务质量与满意度评价标准》设计了调查问卷，得出影响项目运营绩效的32个不确定因素，建立了运营绩效评价指标体系，以此提出了缓冲区动态调整系数及其调整阈值。

4)实证分析验证了考虑合理缓冲的PPP轨道交通项目弹性特许期模型的有效性，可为政府的前期特许期谈判和未来的运营管理提供科学依据，并能有效激励社会资本不断提高运营绩效，使PPP轨道交通项目真正获得成功。

在设定缓冲区动态调整系数时，本文仅考虑了专家的主观意见，未来还需进一步研究更客观的确定方法。此外，缓冲区动态管理时绩效考核的阈值设置亦可进一步探讨和完善。