一类新Durrmeyer型算子在Orlicz空间内的逼近

任美英

(武夷学院数学与计算机学院, 福建 武夷山 354300)

1 引言

近些年来，有关Orlicz空间中算子逼近的研究已取得好些结果[1-12]. 2003年，V.Gupta, P.Maheshwari等学者[13]引进如下一类新Durrmeyer型算子序列{Pn(f; ·)}：

(Ⅰ)

同时，在文献[13]中，作者V.Gupta和 P.Maheshwari还引进并研究了如下Pn(f; ·)的Bezier变形Pn,α(f; ·)的点态收敛速度：

(Ⅱ)

其中

显然，当α=1，Pn,α(f; ·)就退化为Pn(f; ·).

本文的目的是研究算子Pn(f; ·)在Orlicz空间内的逼近性质.

由文献[15]知，ω1,M(f,t)→0 (t→0),ω2,M(f,t)→0 (t→0)当且仅当N函数M(u)满足Δ2-条件.

本文中，c表示与f,n无关的正常数, 在不同处可以表示不同的值.

定理2 设M(·)满足Δ2-条件，则对于

定理3 设M(·)满足Δ2-条件，则对于

2 几个引理

引理1[14]设M(·)为N-函数，则对任意的u,v∈(-∞,+∞)，有

M(u)+M(v)≤M(|u|+|v|).

引理2[13]对于(I) 式给出的算子Pn(f; ·)，有,

(1)Pn(1;x)=1;

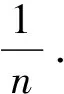
‖g-f‖M≤ω1,M(f,t).

由Cauchy-Schwarz不等式及引理3得

3 定理证明

‖f(0)‖M+‖f‖M.

定理2的证明：对

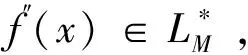
|Pn(t-x;x)‖f′(x)|+|Pn((t-x)2;x)‖θf″(x)|≤

其中0<ξ

(2)对于

‖Pn(f; ·)-f‖M≤‖Pn(f-ft; ·)‖M+‖Pn(ft; ·)-ft‖M+‖ft-f‖M≤