高拱坝深潭型水垫塘数值模拟研究
王 瑶,戴荣强,刁明军
(四川大学水利水电学院,四川 成都 610065)
高拱坝工程大多具有“高水头、大泄量、窄河谷”的特点,其泄洪消能问题一直是设计的重中之重.大量研究表明,挑跌流和水垫塘相结合是高拱坝工程中普遍采用且最为经济的一种坝身泄洪消能型式[1-2].作为消能过程中重要组成部分的水垫塘,其流态演变[3-5]、体型优化[6-7]和受力特征[8-10]是工程失败与否的关键因素,因此水垫塘的优化设计具有一定的理论和实际意义.
在已建的高拱坝工程中,根据水垫塘底板的形状,可分为平底水垫塘和反拱水垫塘两种形式.平底水垫塘的底板往往被设计的很厚来提高自身的重力,以抵抗巨大的荷载,保持稳定[11].反拱水垫塘的底板的稳定性归结为拱座的稳定性,能很好的发挥混凝土的抗压性能,在结构稳定方面优于平底水垫塘[12].近年来随着计算流体力学兴起,CFD数值模拟技术逐渐成熟.孙建、张春财等[13]采用RNGk-ε湍流模型和“刚盖”法对反拱水垫塘与平底水垫塘的流场进行了数值模拟研究,并对比了两种水垫塘在冲击区以及上下游的流态、流速以及压强分布的合理性.丰小玲等[14]采用二维VOF方法对高拱坝表深孔空中碰撞泄洪下的水垫塘流场进行了数值模拟展示水流发展的全过程.张为、陈和春等[15]采用k-ε湍流模型模拟了块体与平底水垫塘内水流的运动特性,并对两种水垫塘流速衰减程度和消能率进行对比分析.王英奎、廖仁强[16]等以淹没冲击射流和淹没水跃理论为基础,总结了水垫塘的消能机理和过程,并提出“深水垫条件下的水垫塘消能方案设计”可作为高拱坝的进一步研究方向.
上述研究表明,水垫塘内的流态可看做淹没冲击射流和淹没水跃的混合流态,水垫塘的设计要点包括水垫塘深度和长度.水垫深度是制约水垫塘消能率的重要因素,水垫深度大,消能效果好[17].水垫塘的长度是由射流的最远挑距与淹没水跃的长度来决定的[18],为使下泄水体在塘内充分消能,水垫塘的长度往往较大,而实际参与消能的水体并不多,同时为确保水垫塘在运行中不至于受到高速水流的冲刷破坏,对其底板及两岸边坡一般都要用混凝土进行全面的衬砌防护[19],工程费用高,因此本研究期望利用深潭来增大主消能区的水垫深度,实现射流水股的集中消能,并缩短水垫塘的长度以达到降低工程费用的目的.为此,以溪洛渡水电站为研究背景,在八深孔泄洪工况下对反拱水垫塘(坝身深孔和下游水垫塘布置均采用溪洛渡原体型)和深潭水垫塘(降低坝身深孔出口高程以减小挑距、局部开挖深潭并将二道坝向上游移动)进行三维数值模拟,并分析塘内水流流态、流速、压强及消能率,以期使下泄水体在深潭内能够充分消能的情况下减小原水垫塘的长度,同时为实际工程水垫塘设计及应用提供参考.
1 计算模型
1.1 计算域
本研究以溪洛渡水电站的坝身的八深孔和下游水垫塘为研究对象.溪洛渡水电站位于金沙江干流的下游河段(攀枝花-宜宾)四川省雷波县和云南省永善县间的溪洛渡峡谷中,是一座以发电为主,兼有拦沙、防洪和改善下游航运等综合效益的大型水电站.水库正常蓄水位600 m,相应库容115.7 亿m3.图1给出了反拱和深潭水垫塘以及各自相应的深孔布置示意图,二者仅出口高程不一致,出口尺寸均为5×8 m.表1给出八深孔的具体布置参数.计算域坐标原点位于坝轴线与水垫塘底板中轴线的交汇处,高程为330 m.x轴沿塘底板中轴线指向下游为正,z轴为-g方向,y轴垂直xz平面指向左岸为正,z与实际高程的关系为:z=实际高程-330 m.

表1 深孔体型参数
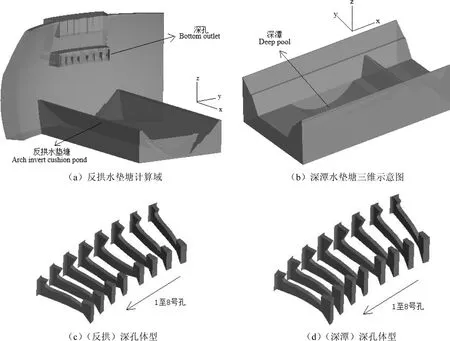
图1 计算域示意图
图2给出了两种水垫塘的剖面示意图.如图2(a)所示,反拱水垫塘底板半径R=81.25 m,圆心角θ=77.76°,拱底板最低高程为335 m,两岸拱圈之间距离为102 m,两拱座之间距离为109 m,高程为360 m,拱座处设有宽5 m的马道,再连接坡度为1:1的边墙.反拱水垫塘中二道坝的桩号为X+400 m,顶宽7 m,高程为375.5 m,上、下游坡度分别为1:0.6和1:0.8.如图2(b)、(c)所示,深潭水垫塘在原来底板最低高程335 m的基础上再下挖40 m,深潭沿x方向长175 m、沿y方向宽121 m(依据各工况的水舌挑距和入水宽度而定),纵剖面深潭的半径R=115.7 m,圆心角θ=98°,深潭水垫塘中二道坝的形状和大小不变,桩号为X+320 m(依据数值计算中的水流流态而定).
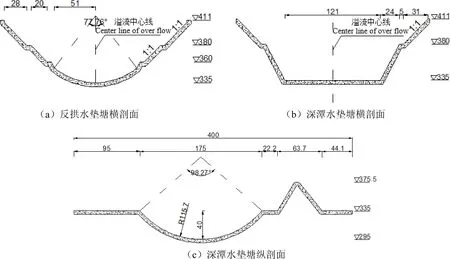
图2 水垫塘剖面示意图
1.2 控制方程
本研究的模型属于不可压缩流体的湍流流动,由以下连续方程和动量方程描述:
(1)
(2)
式中:ρ为流体的密度;ui,uj为流体速度分量,i=1,2,3、j=1,2,3;xi,xj为坐标分量;p为压强;fi为质量力;v为运动粘性系数.
本研究采用RNGk-ε湍流模型可以较好地适应流线弯曲程度较大的水流运动,k方程和ε方程如下:
(3)
(4)
式中:k为湍动能;ε为湍动能耗散率;ueff=u+ui,u为流体动力粘滞系数,ui为流体湍动粘度;Gk为由于平均速度梯度引起的湍动能产生项;一般αk=αε=1.39,C1ε=1.42,C2ε=1.68.
1.3 网格划分及计算方法
计算域中网格单元全部采用六面体结构,网格单元的长宽高均设置为1.5 m,并采用嵌套网格对关键的深孔结构特征处进行局部加密.Flow-3D中的Favor技术可解决网络模型失真问题,通过 Favor技术对网格进行划分,并采用有限差分法离散控制方程为代数方程组进行数值求解,对流项采取二阶迎风格式,扩散项采取二阶中心差分格式,求解器选择GMRES并采用默认设置选项,最小步长设置为10-7s.采用的Tru-VOF只计算含有液体的单元而不考虑只含有气体的单元,相对于传统的VOF(Volume of fluid)法很大程度的减少了模型收敛所需时间,该方法是对VOF技术的进一步改进,能够准确地追踪自由液面的变化情况,使其能够精确地模拟具有自由液面的流动问题,可精确计算动态自由液面的交界聚合和飞溅流动[20-21].
1.4 边界条件
图3给出了计算域边界条件的设定,其中上游库区进口设定为流量进口,基于试验结果设置流量值为12 206 m3/s,同时设置上游控制水位为600 m,不指定运动方向,默认来流从开放区域垂直边界流入;水垫塘出口设定为压力边界并设置下游控制水位为390 m;模型底面和左右岸边壁均设定为固壁边界,即非滑移壁面边界;模型顶面设定为压力边界,没有水流存在,仅有气体;嵌套块四周均设为对称边界条件,其物理量的法向导数为0.
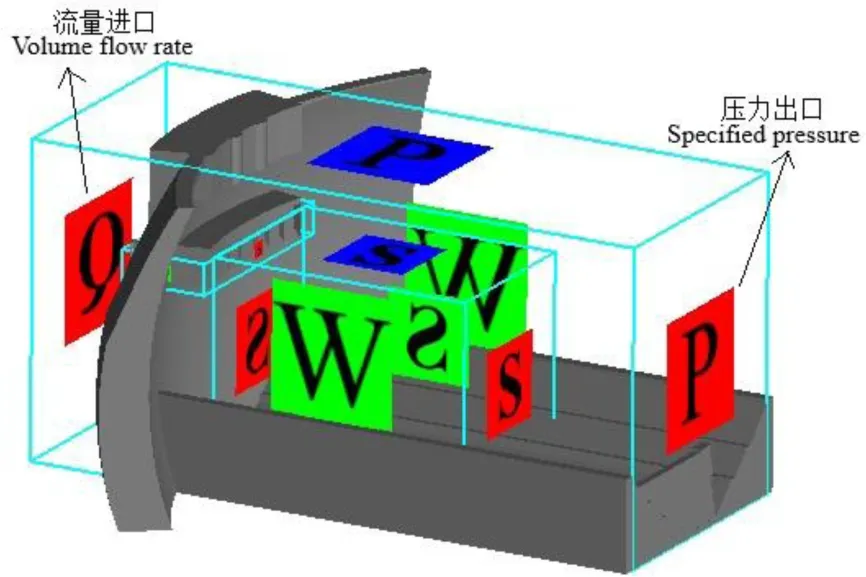
图3 边界条件设置
2 数模可靠性验证
图4和图5分别给出了八表孔泄洪条件下反拱水垫塘内二道坝顶流速、沿程近壁流速和底板压强的计算值与实测值之间的比较.从图4(a)可知二道坝顶流速实测最大值为10.26 m/s,而计算最大值10.23 m/s;从图4(b)可知水垫塘内近壁流速的实测值与计算值吻合度较高,最大相对误差为13.5%.从图5(a)、(b)及(c)可知,塘内横断面x=170 m、190 m及220 m底板压强实测值和计算值吻合度较高,由图5(d)、(e)可知从x=230 m处至下游压强计算值普遍高于实测值,最大相对误差为11.2%,这是因为比尺效应和模拟计算的边界条件的限制所致.因此综合流速和压强实测与计算对比结果,认为采用RNGk-ε紊流数学模型来模拟溪洛渡泄洪消能的过程是可行的.

图4 水垫塘内流速计算值与实测值对比
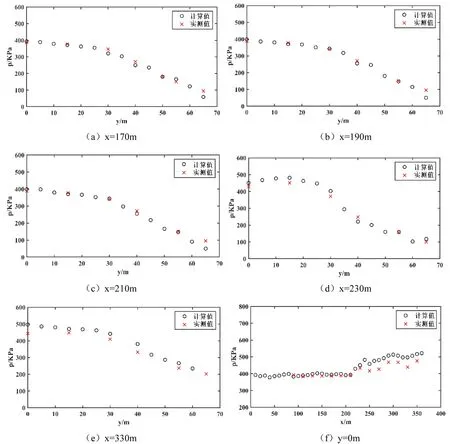
图5 水垫塘内流速和压强计算值与实测值对比
4 水垫塘流场特性分析
4.1 塘内水流流态
图6给出了两种水垫塘的坝身泄流水舌空中运动及入水情况.如图6(a)所示,水舌入水范围为x=0+170 m~x=0+260 m,入水角44°~52°.如图6(b)所示,水舌入水范围为x=0+140 m~x=0+190 m,入水角48°~56°.
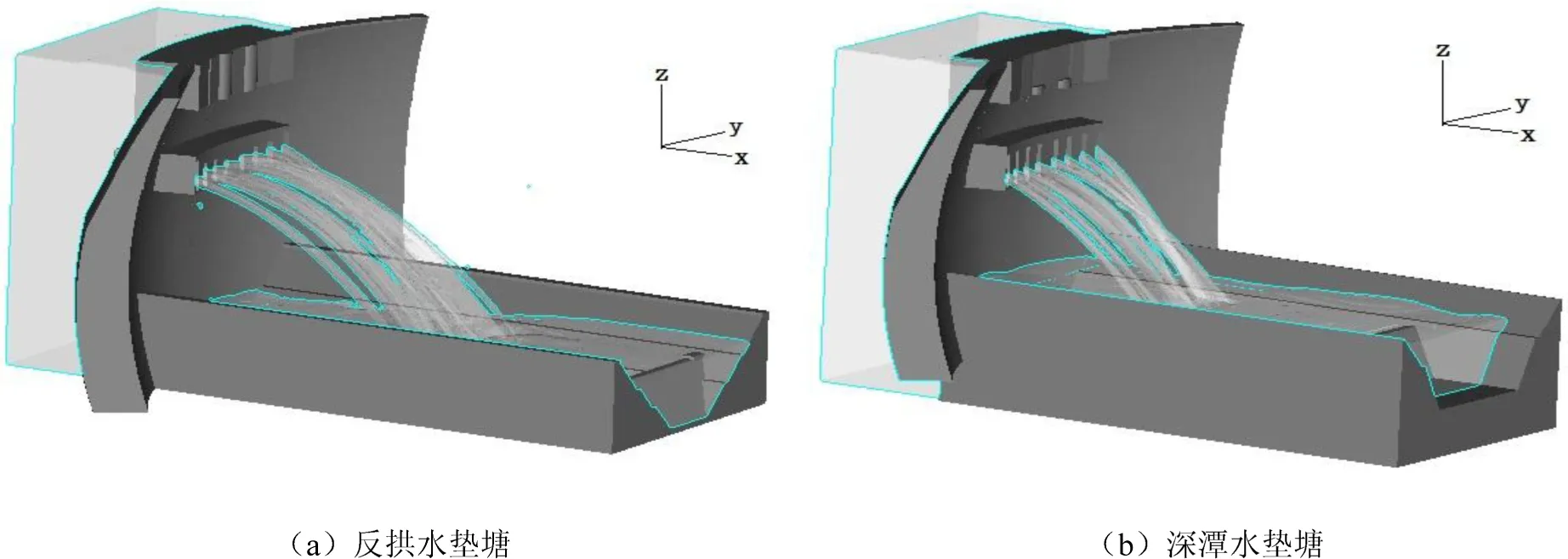
图6 泄流水舌空中运动示意图Fig.6 Schematic diagram of air movement of spillway jets
图7给出了两种水垫塘的纵向流速矢量分布图.由图7(a)可知反拱水垫塘内水流流态为淹没冲击射流,射流水股经底板折冲后大部分向下游方向、另一部分沿上游和横向发展形成贴壁流,下游纵向贴壁流沿程射出并迅速跃起,其上方为水跃漩滚区,该区域临近自由液面导致水面波动剧烈,跃后水体经二道坝平稳流出.由图7(b)、(c)可知射流水股入水垫塘后,沿深潭弧面向上、下游运动的水流由于深潭顶端、二道坝和塘内坝身附近水体的作用折回深潭形成主横向漩涡,并带动附近水体不断紊动、剪切消能,还有部分水体沿横向发展.由于深潭区域水垫深度较大,漩涡基本在水面下发展,二道坝后流线平顺,水面平稳无明显波动.两种水垫塘由于射流水股的入水角不同导致其向上下游方向运动的水体的比例不同.深潭水垫塘内的上游区域水流较为平顺,而反拱水垫塘仍存在由入水区发展而来的横向漩涡.深潭水垫塘内水面波动较反拱水垫塘弱,考虑其产生涌浪的可能性较低.
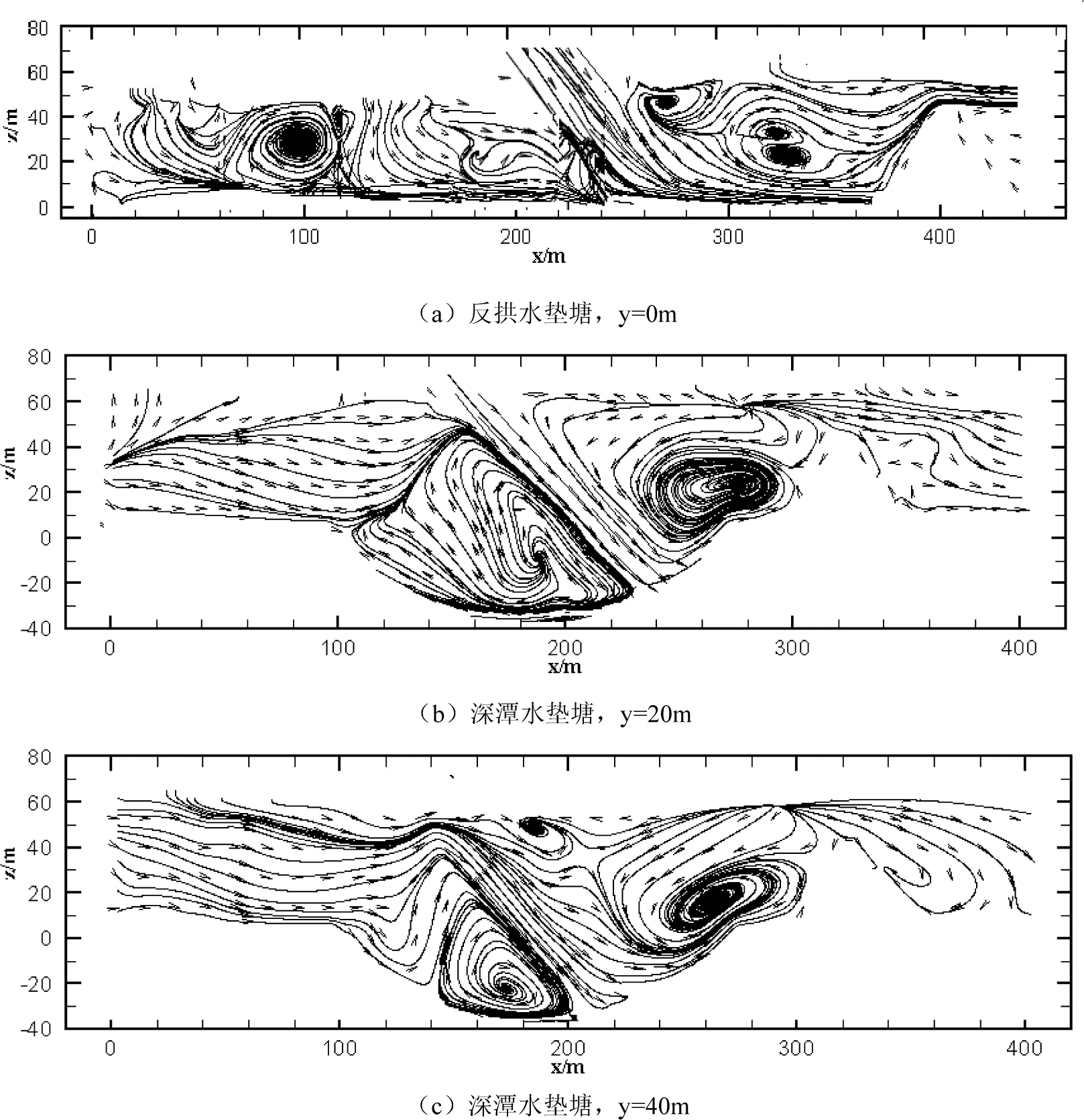
图7 水垫塘纵断面流态及流速矢量分布
图8分别给出了两种水垫塘横断面(水舌入水区上游,入水区、入水区下游)流速矢量分布图.在水舌入水区上游,由图8(a)可知水流从两岸向中心运动,在溢流中心线附近形成两个漩涡,同时带动其下方水体沿反拱曲面向两岸运动.由图8(b)可知由深潭内发展而来的两股水流一部分在溢流中心线附近汇集折回深潭,另一部分合成一股向右岸水面运动.
在水舌入水区,从图8(c)中可以看到两股水舌经底板折冲后沿反拱曲面形成横向贴壁流,一部分向溢流中心运动形成多个纵向漩涡,另一部分以逐渐增大的速度向两侧运动,到达左右拱端时流速大小分别为23.44 m/s和22.34 m/s,随后贴壁流越过马道继续斜向上运动,水面波动剧烈.由图8(d)可知贴壁流向两岸方向运动,分别以10.23 m/s和10.84 m/s的流速冲击边坡隅角后再沿两侧边墙射出,射出流速分别为10.61 m/s和12.75 m/s.由于深潭内水垫深度较大,入水区沿横向形成多个大尺寸漩涡,水体间紊动剧烈,消能充分.
在入水区下游,由图8(e)可知主流由于二道坝的作用向上运动,断面中部仍存在由入水区发展而来的漩涡.由图8(f)可知水流整体向水面运动,这是由深潭内的水体发展而来.漩涡发展空间较反拱水垫塘大.
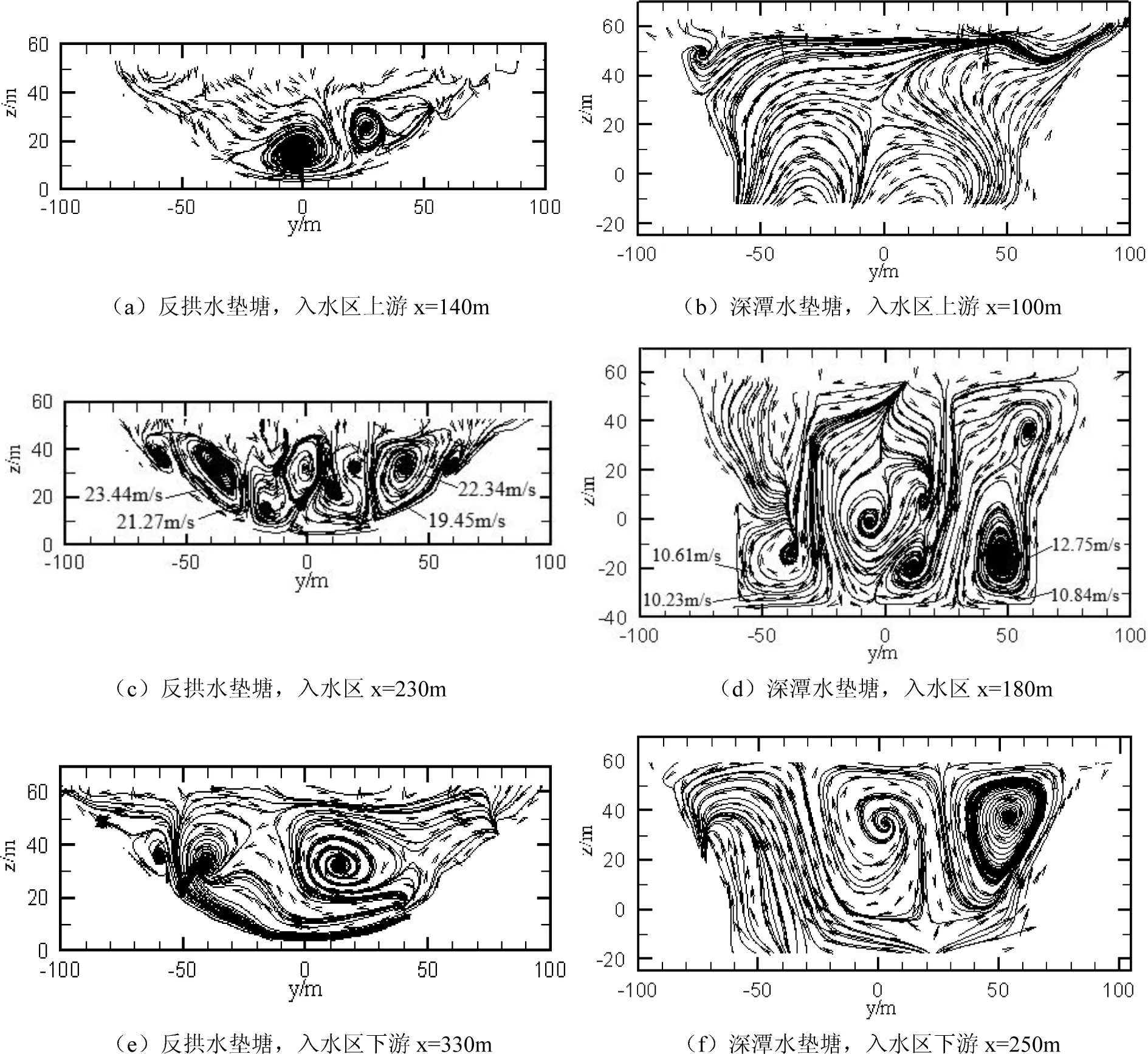
图8 水垫塘横断面流态及流速矢量分布
4.2 塘内近壁流速分布
图9给出了两种水垫塘内近壁流速的沿程变化,可知两种水垫塘的近壁流速沿横向大致呈现溢流中心线附近大,向两岸方向递减的发展趋势.由图9(a)可知反拱水垫塘近壁流速纵向发展趋势: x=190 m断面上游流速在0 m/s附近波动,变化不大;从x=190 m断面向下游方向流速为正且迅速增至峰值又缓慢降低,沿程近壁流速最大值为23.58 m/s,反向最大流速为5.97 m/s,二道坝前40 m断面最大近壁流速为10.27 m/s.由图9(b)可知深潭水垫塘内x=0 m~90 m范围近壁流速在0 m/s~2.5 m/s之间波动;深潭圆弧起始处(x=100 m)流速矢量开始转向,流速为负,此处代表射流水舌经底板折冲至上游;从x=230 m断面向下游方向近壁流速增至峰值又降低,沿程近壁流速最大值为15.99 m/s,反向最大流速为10.49 m/s,二道坝前40 m断面最大近壁流速为3.54 m/s.分析可得反拱水垫塘内近壁流速沿横向衰减较快,但初值较高,深潭水垫塘沿纵向衰减较快,二道坝前近壁流速较反拱水垫塘低,消能效果更好.
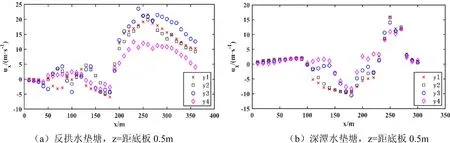
图9 水垫塘临底流速纵向分布
4.3 塘内压强特征分布
图10给出了前两种水垫塘底板压强的比较,二者压强计算值均以底板最低高程为准.由图10(a)可知八深孔泄洪条件下反拱水垫塘上游静水区的水流无明显紊动,压强较小;从x=200 m处压强开始增加但幅度较小,底板压强最大值575.27 KPa,相应最大冲击压强为8.64 mH2O;水垫塘下游压强无明显降低.由图10(b)可知,深潭水垫塘底板x=180 m~230 m为压强峰值区,峰值区以外底板压强沿纵向明显降低,底板最大压强为1 066.35 KPa,相应最大冲击压强为11.62 mH2O.深潭水垫塘底板压强较大的原因一是坝身深孔的挑流水舌挑距较小、入水角较大,二是深潭的水垫深度较大,潭内集中消能.
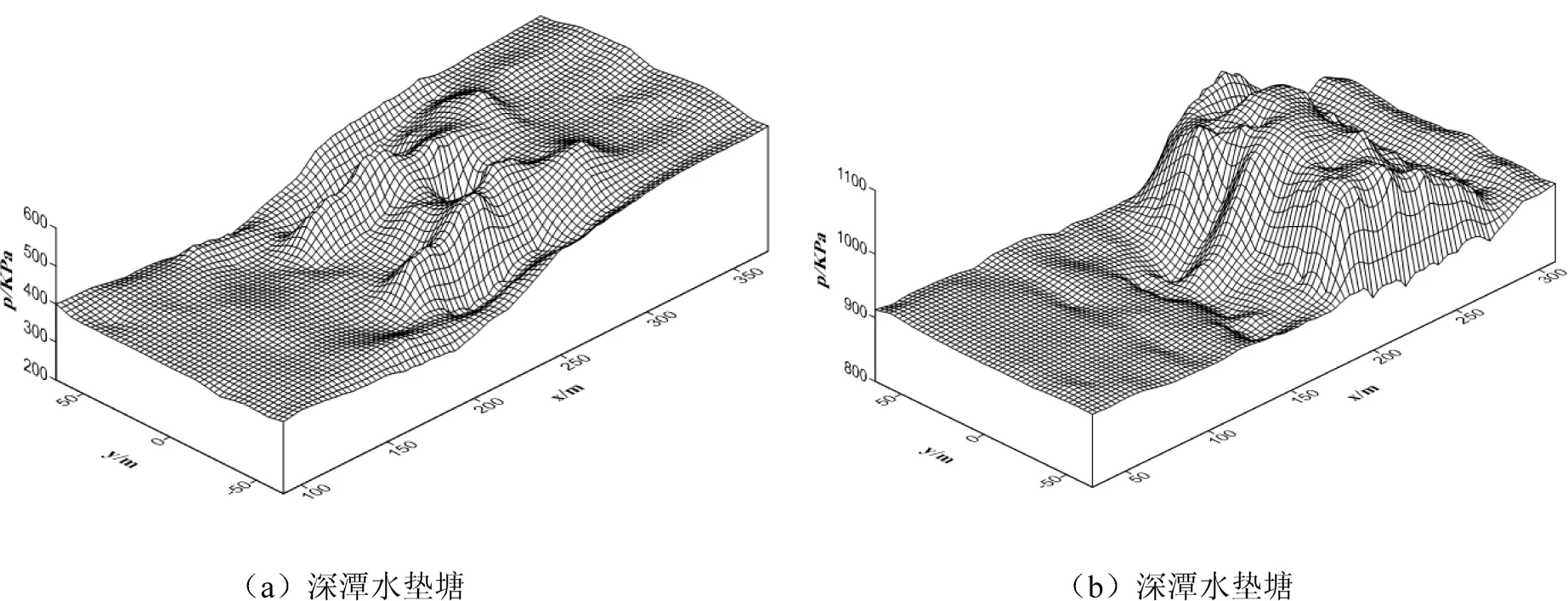
图10 水垫塘底板压强分布
4.4 消能率的比较
高拱坝下泄水体能量耗散主要以水垫塘内的能量耗散为主,水舌的空中耗散为辅.假定库区的进口处为0-0断面,水垫塘二道坝顶断面处为1-1断面,对0-0和1-1断面列出能量方程,有:
(5)
(6)
根据上述连个方程,可以得到消能率为:
(7)
其中,η为消能率;v0、v1分别为0-0断面和1-1断面的平均流速.z0、z1为两个断面的位置水头,p0、p1为断面的大气压强.
反拱和深潭水垫塘二道坝顶部平均流速分别为8.52 m/s和5.34 m/s,消能率分别为90.25%和92.25%,显然深潭水垫塘的消能率高于反拱水垫塘.
5 结论
结合溪洛渡水电站,对反拱水垫塘和深潭水垫塘进行三维数值模拟研究,得到结论:反拱水垫塘内射流水体经底板折冲后,大部分沿下游方向发展,小部分沿上游和横向发展,塘内水流流态复杂,具有淹没水跃特征,跃后水体经二道坝平稳流出.深潭水垫塘由于坝身深孔的布置使得水舌入水角增大,同时深潭的布置使得水垫深度加大,下泄水舌经底板折冲后沿上下游方向发展的水体体积相差不大,这就反映了深潭内近壁流速绝对值小于反拱水垫塘的现象,但也正因如此导致了深潭底板冲击压强大于反拱水垫塘.由于深潭上游水体、深潭边壁和二道坝的作用,贴壁流返回深潭内充分消能,二道坝后流线平顺,坝顶平均流速小于反拱水垫塘,消能效果更好.因此,深潭水垫塘在保证高拱坝下泄水体充分消能的情况下能够有效缩短水垫塘长度.

