基于Bandit反馈的在线分布式镜面下降算法

朱小梅，李觉友

1. 重庆师范大学 数学科学学院，重庆 401331； 2. 重庆两江新区博雅小学校，重庆 401121

随着数据规模的爆炸式增长，集中式优化算法因受限于单机的计算瓶颈而难以求解大规模优化问题．而多机协作的分布式机制可以大大降低单机的计算负担．同时，在分布式网络中，节点之间通过相互协作，可以有效解决诸如智能电网、传感器网络等大规模问题，并能提高数据传递效率，增强网络鲁棒性[1]．但在应用中，分布式网络通常是动态变化的，而在线学习具有实时更新模型的特性，能够根据数据的变化动态地调整模型[2]，进而可高效地完成对大量实时数据的处理，已经在机器学习、在线推荐系统和资源分配等方面体现出了重要的应用价值。

然而，上述大多数算法都需要计算梯度．但在许多实际应用场景中，梯度信息往往难以获取．因此，设计出一种免梯度计算的有效算法显得非常有意义．受文献[9]的启发，本文提出了一种基于Bandit反馈的免梯度在线分布式镜面下降算法．不同于ODMD算法，我们提出的算法只需要简单计算函数值，主要是利用损失函数在一些随机点的函数值信息去逼近损失函数的梯度，从而避免了直接计算损失函数的梯度．我们设计的算法主要有两个优点：① 能有效解决梯度信息难以获取的困难； ② 能有效处理约束集较复杂(如单纯形约束集)的优化问题。

1 准备工作

1.1 图论

1.2 Bregman散度

定义2[8](Bregman散度) 设h(·)是1-强凸函数，定义如下关于函数h的Bregman散度Dh(·，·)

Dh(x，y)=h(x)-h(y)-〈x-y，h(y)〉

Euclidean距离和Kullback-Leiber(KL)散度为两种常用的Bregman散度。

结合定义1和2可以得到有关Bregman散度的一个重要性质[8]

(1)

(2)

1.3 Bandit反馈

现有在线分布式算法大多是基于完全信息设计的，即节点可以获得其决策空间中任何一个位置的梯度信息．而在许多应用场景中，节点一般获得的是带噪音的、有缺漏或有限的信息反馈，称这种不能直接获得损失函数梯度的情形为Bandit反馈机制[9]，即节点只能访问自身损失函数在一些随机点上的函数值，但并不知道其梯度信息．众所周知，大多数优化算法的设计是基于损失函数的梯度设计的，而在Bandit反馈中，面临着梯度信息不可用的问题．为此，我们设计了仅利用损失函数值来逼近梯度的Bandit算法．下面给出根据函数在随机点上的函数值来近似估计其梯度的一些结果。

(3)

其中U(B)表示服从单位球B={x∈Rm|‖x‖≤1}的均匀分布，E[·]表示期望。

引理2[9]设S={x∈Rm|‖x‖=1}表示Rm中的单位球面，有以下结果：

2 问题与算法

2.1 问题

考虑图G=(V，E)上的在线分布式凸优化问题如下

(4)

(5)

假设2对∀i∈V和∀t∈{1，…，T}，fi，t(·)在χ上是G-Lipschitz连续的，即对∀x，y∈χ，有|fi，t(x)-fi，t(y)|≤G‖x-y‖。

由假设2知fi，t(·)的次梯度fi，t(·)在χ上是一致有界的，即‖fi，t‖≤G。

2.2 基于Bandit反馈的在线分布式镜面下降算法

由光滑化函数的定义(3)，我们给出问题(4)中节点i在时刻t的损失函数fi，t的一个光滑化函数

(6)

(7)

在时刻t，只有xi，t被确定后才可以获得fi，t，进而才能估计fi，t(xi，t±ξui，t)，其中ui，t～U(S)。

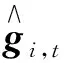
(8)

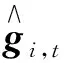
(9)

算法1ODMD-B算法

1) 输入：最大迭代次数T，步长ηt，收缩系数α，光滑化参数ξ；

2) 初始化：xi，1∈(1-α)χ，yi，1=xi，1，∀i∈V；

3) fort=1，…，Tdo

4) fori=1，…，Ndo

5) 利用决策xi，t，观测局部即时损失函数fi，t(x)；

8) end for

9) end for

3 收敛性分析

这一部分主要论述本文提出的ODMD-B算法在局部损失函数为凸时的Regret界．分析思路如下：首先，估计出各节点的网络化误差，见引理4； 然后，引入一个辅助函数并给出一个重要的引理，见引理5； 最后，根据已建立的结果得出主要结果。

引理3[8]如果假设1和2均成立，且Dh(x，y)关于第二个变量y是凸的，则

(10)

引理4如果假设1和2均成立，序列{xi，t}是由算法1迭代产生的，则对任意的i∈V和t≥1，有

(11)

证根据算法1的步7)和引理1，有

由(1)式可得

(12)

(13)

由(13)式和假设1可得

(14)

于是由(13)式和(14)式有

利用双随机矩阵A的性质[8]，即矩阵A满足

(15)

这样有

(16)

为了证明定理1的结果，对任意的x∈χ，作如下辅助函数

(17)

引理5如果假设1和2均成立，序列{xi，t}是由算法1迭代产生的，则

(18)

(19)

接下来对(19)式最后一个不等式右边的三项分别进行估计．对第一项，根据算法1的步8和引理4，有

(20)

对第二项，由(9)式有

(21)

其中(21)式的最后一个不等式由均值不等式得到．对第三项，根据引理1和(1)式，有

(22)

最后，将(20)-(22)式代入(19)式，且在(19)式中对t=1，…，T求和，然后再对i=1，…，N求和，最后利用引理3可证得(18)式成立。

(23)

其中

证根据Regret界的定义(5)式及ft的G-Lipschitz连续性，有

(24)

在(24)式中，利用引理4，可得

(25)

在(25)式中，先对t=1，…，T求和，然后再对i=1，…，N求和，可得

(26)

(27)

从而

(28)

(29)

从而由(29)式可得

(30)

根据(28)式和(30)式，由(26)式右边的项得

(31)

由Fi，t(·)的定义，有

(32)

(33)

对(26)式取期望，结合(31)式和(33)式，再根据引理5，有

(34)

4 数值实验

为了说明算法的有效性，考虑一个不对股票市场进行任何统计假设的投资组合选择模型，被称为“通用投资组合选择”模型，它在在线学习中受到了特别的关注．下面给出一个投资组合选择模型[10]

(35)

其中q=1，…，m．对于ODMD-B算法的性能度量，考虑平均Regret界．另外，将本文提出的ODMD-B算法与文献[8]提出的ODMD算法进行数值对比。

首先，考虑不同的问题维数对ODMD-B算法性能的影响．图1a和图1b分别表示N=10，m=50和N=10，m=100的平均Regret界随着迭代次数变化的演化图．从图1a和图1b可以看出，本文提出的ODMD-B算法与文献[8]提出的ODMD算法都可以收敛．但ODMD-B算法的早期收敛速度稍微慢于ODMD算法，这是因为ODMD-B算法只使用了函数值信息，而ODMD算法是直接使用了梯度信息．但随着迭代次数增大，ODMD-B算法的平均Regret界大致接近ODMD算法的平均Regret界．另外，对比图1a和图1b中的ODMD-B算法，当T=700时，m=50和m=100平均Regret界分别为0.020 52和0.027 39，仅相差0.007左右．这表明问题维数对所提算法性能的影响并不大，这主要是因为此问题在迭代过程中能够求得显示解。

然后，考虑不同的节点个数对ODMD-B算法性能的影响．图1c和图1d分别表示N=50，m=100和N=100，m=100的平均Regret界随着迭代次数变化的演化图．图1c和图1d进一步表明两种算法的平均Regret界随着迭代次数的增加而趋于一致．另外，对比图1c和图1d可以发现，随着节点个数的增加，两种算法的平均Regret界随之增加．相比ODMD算法，本文所提ODMD-B算法仅仅使用了函数值信息。

图1 ODMD-B算法与ODMD算法平均Regret界的比较

5 结论