基于马氏距离结合自适应滤波的协同定位方法

徐 博，王权达，李盛新，王连钊

（哈尔滨工程大学 智能科学与工程学院，哈尔滨 150001）

我国是海洋大国，拥有四大海域，海洋面积辽阔。人类也从未停止过对海洋的探索，但是由于海洋环境复杂、条件恶劣，大约95%的水下区域都还没有被探索。自主式水下机器人（Autonomous Underwater Vehicles, AUV）作为一种海上无人智能装备，已广泛应用于海上各个领域，由于人类文明的深化，在海洋勘探开发活动中，使用单AUV已经不能满足当前的任务要求。因此，基于水声通信网络的多AUV的协同定位技术受到了更多的关注[1]。世界各国总体都在朝着多AUV、UUV的自主、智能协同作战方向发展，但是各国偏重有所不同。美国从海洋数据搜集和海底探测向着潜艇协同作战和协同反潜发展。葡萄牙近几年也侧重于反潜、跟踪。英国和欧盟近几年的项目侧重于海洋采样和数据搜集[2-5]。协同定位技术在未来会有更广泛的应用。

目前即使使用精度最高的惯性传感器，导航参数也会产生漂移现象，从而导致定位误差发散，最终引起较大的误差。因此找到一种能够抑制这一误差的方法就尤为重要，如果将主从AUV水声距离通信应用于导航系统中，结合信息融合技术就可以抑制此类误差，这种方法被称为协同定位技术，这是一种水下定位技术，是针对水下航行器协同应用而发展起来的[6,7]。在水下协同导航系统中，主AUV需装配精度较高的导航系统，以便获取高精度的导航信息，从AUV一般装配低精度的惯性导航系统（Inertial Navigation System, INS），主AUV和从AUV通过水下声学调制解调器进行通信以此提高从AUV定位精度。AUV间利用水声通信来共享彼此的导航信息，利用水声测距获取相对距离作为观测量，然后利用数据融合技术来降低定位误差[8]。由于多艇协同定位可以提高系统整体的定位能力，而且具有成本低、系统鲁棒性好的优点，可以极大地增强多AUV系统的任务执行能力，具有重要的理论和应用价值。水下环境是复杂且多变的，因此AUV在航行过程中会遇到很多不确定情况，导致量测信息出现野值或不更新等故障，这将会对协同导航系统定位精度带来很大影响[9,10]。因此，设计能提高多AUV协同定位精度的故障诊断算法是至关重要的。

卡尔曼滤波算法在导航领域的应用非常广泛，协同导航领域也不例外，由于在协同定位系统中，系统模型和量测方程都是非线性的，因此需要使用非线性卡尔曼滤波算法进行协同定位。容积卡尔曼滤波（Cubature Kalman Filter, CKF）算法在处理非线性模型时相比扩展卡尔曼滤波算法和无迹卡尔曼滤波算法滤波精度更高，实时性更好[11-13]。CKF利用点估计方法，提高了拟合精度，同时也避免了数值不稳定现象。文献[14]将容积卡尔曼滤波方法与无迹卡尔曼滤波进行对比，结果表明容积卡尔曼滤波算法精度更高、适用范围更广尤其针对高维非线性系统。

马氏距离（Mahalanobis Distance, MD）是一种距离的度量，它独立于量测尺度，不受量纲的影响，可以有效排除变量之间的相互影响[15,16]。本文使用滤波新息的马氏距离作为量测异常的检验统计量，判断水声传感器是否发生故障。针对协同导航在噪声统计特性不确定和传感器出现故障时量测信息不更新的问题。文献[17]利用误差开窗拟合来解决量测异常问题，但这种方法不利于对数据进行实时处理，数据存储量较大。文献[18]利用两次卡方检测来进行故障诊断，在标准CKF、抗差滤波和自适应滤波中进行选择。但它并不能处理系统同时存在量测异常和噪声不确定的状况。本文将利用新息序列马氏距离对量测系统进行评估，再利用自适应容积卡尔曼滤波算法实现协同导航系统的实时数据融合，提出了基于新息序列马氏距离结合自适应容积卡尔曼滤波算法（MD-ACKF）。本文的主要贡献是提高了在量测异常情况下多艇协同导航精度，减小了异常量测对协同导航精度的影响。

1 AUV协同定位系统描述

目前水下协同定位主要分为两类方式，并行式和主从式，考虑到在保证精度的前提下尽量减小设备成本的问题，本文主要研究基于主-从编队协同定位的方法。在主从式协同定位方法中，也分为单领航和多领航模式，考虑到可观测性问题，如果在单领航模式中，主AUV与从AUV在特殊的航行路线下，会导致可观测性不足，进而导致协同定位系统失效，定位误差发散，因此本文所研究的系统为双AUV交替领航系统，来提高系统可观测性。其中主AUV配备高精度的导航设备，该系统承担通信和导航设备（Communication and Navigation Aid, CNA）的作用；从AUV只依靠多普勒速度计程仪、罗经和深度传感器提供的信息进行航位推算。

首先建立描述AUV协同导航系统的状态方程和量测方程。AUV在运动时的俯仰角θ较小，可近似cosθ≈1，同时深度压力传感器可以提供水下航行器的深度信息，因此可将协同定位运动模型简化为二维模型。

定义AUV在tk时刻的平面运动状态为可以得到状态空间模型为：

式中，λk表示tk时刻的经度；Lk分别表示tk时刻的纬度；Δt为状态采样时间；vk为前向速度；ωk右舷速度；θk为AUV航向角，航向角为AUV的前向与北向的夹角；hk为从AUV的深度信息；为过程噪声向量；RM,k和RN,k分别为子午线的曲率半径和卯酉线的曲率半径，定义为：

式中，Re=6378137 m，e=1/298.257。

主AUV与从AUV都安装了水声调制解调器，CNA周期性的向从AUV发送自身的位置信息。CNA与从AUV之间的距离可以通过基于到达时间（TOA）定位方法来测量，定义CNA在tk时刻的运动状态为CNA与从AUV之间的相对距离为：

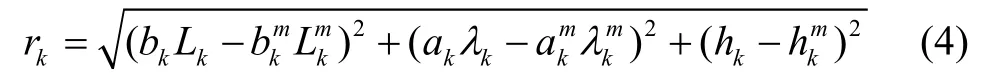
式中，rk为CNA与从AUV之间的相对距离；为CNA的深度；ak、bk、、定义如下：

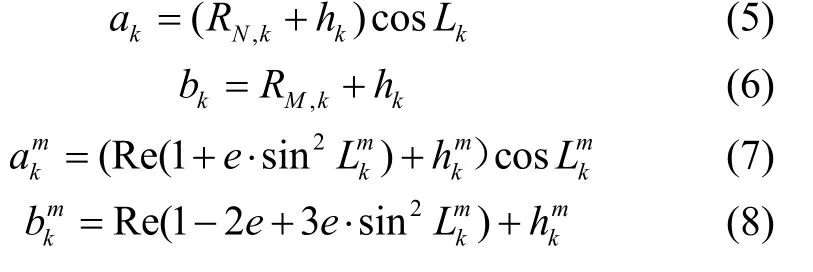
由于深度信息可由压力深度传感器获取，因此距离量测方程可简化为：

式中，δk为量测噪声。

基于式(1)和(9)建立多AUV协同定位系统的离散时间状态空间模型：

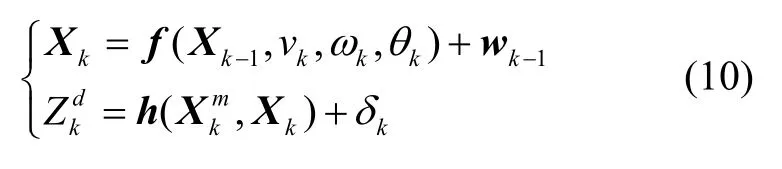
式中，f(Xk-1,vk,ωk,θk)和分别为状态转移函数和量测函数，定义为：

式中，wk-1～N(0,Qk-1)和是互不相关的高斯白噪声，Qk-1和分别为过程噪声协方差矩阵和测量噪声方差。

2 CKF算法

2.1 CKF算法

CKF滤波算法的基础是Gaussian滤波。对于一般的非线性离散系统可以用以下方程表示：

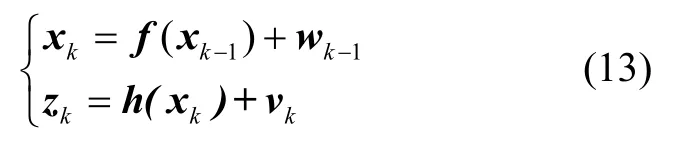
式中，xk∈Rn为n×1维状态向量；zk∈Rm为mz×1维量测向量；f（·）和h（·）为已知函数，系统噪声wk和测量噪声vk均服从Gaussian分布N(0,Q),并且能由均值和方差完全表征。

对于非线性系统(13)，容积卡尔曼滤波算法的计算步骤如下：预测步骤为：

Step 1: 对协方差矩阵Pk-1/k-1采用Cholesky分解。

Step 2: 计算容积点(i= 1,2…m)。

其中m=2n。

Step 3: 计算预测状态容积点。

Step 4: 估计预测状态。

Step 5: 估计预测协方差。

更新步骤为：

Step 1: 预测协方差矩阵进行Cholesky分解。

Step 2: 计算容积点(i= 1,2…m)。

Step 3: 计算预测量测容积点。

Step 4: 估计预测量测。

Step 5: 估计新息协方差。

Step 6: 估计互协方差矩阵。

Step 7: 计算卡尔曼滤波增益。

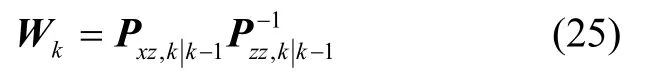
Step 8: 估计状态更新。

Step 9: 估计状态协方差。

2.2 自适应CKF算法

为进一步提升CKF算法滤波性能以应对系统波动较大等情况，提高算法的自适应与鲁棒性，将CKF算法进行改进。由CKF算法原理可知，影响滤波精度的参数主要是卡尔曼增益Kk+1，而协方差矩阵与互协方差矩阵可以决定Kk+1的大小。因此本文构造了可以对协方差矩阵进行实时修正的自适应因子，实现方法如下：

容积卡尔曼滤波基础算法不做改变，通过定义新息向量式(28)以及新息向量矩阵式(29)，判断Δek与自协方差矩阵迹的大小来构造自适应因子。具体实现如下：

由式(30)，当量测异常或系统出现突变现象时，zk和之间的绝对误差会增大，导致Δe变大，由于矩阵之间不能直接进行大小的比较，因此我们用矩阵的迹来衡量矩阵的大小，当Δe的迹大于迹，就需要对预测误差方差阵进行修正来保证滤波结果的准确性。

自协方差矩阵修正：

互协方差矩阵修正：

至此完成k时刻的滤波修正过程。

3 基于新息序列马氏距离辅助自适应CKF

马氏距离是一种很有效的计算样本集相似度的方法，它由数据的各种特性决定，而不是只取决于单一的距离尺度。因此马氏距离相对于欧式距离在某些数据的处理上有很大的优势。对于一个均值为μ=（μ1，μ2，μ3…μn）T，协方差矩阵为∑的多变量向量x=（x1，x2，x3…xn）T，其马氏距离为：

本文中卡尔曼滤波器的量测新息可以表示为：

因此量测新息的马氏距离为：

其中δzd为量测新息，μz为新息序列均值，为量测新息方差。

在本文中卡尔曼滤波器的量测为AUV间的相对距离，因此新息dzδ为一维向量，可以推出因此式(35)可以简化为：

卡尔曼滤波的正交性是指系统模型确定时，如果不存在系统模型误差，卡尔曼滤波所输出的量测新息序列为零均值高斯白噪声。根据卡尔曼滤波的正交性原理可知：

①μz=0

由①和②可以推出量测新息的马氏距离DM(δzd) ～N（ 0,1）。

因此造如下卡方检验统计量：

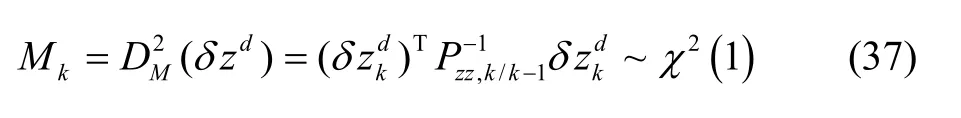
式中Mk服从自由度为1的卡方分布。

若量测出现异常或存在系统突变时，量测新息的马氏距离的平方就不再服从卡方分布，因此可以通过这种方法，利用假设检验原理对系统进行评估。

判断过程为：通过设置卡方检验显著性水平α，可得显著性水平α下的马氏距离的置信概率为P(Mk≤（n）) =1-α。此时系统故障检测过程为：

若Mk＞（n），判定系统有故障；

若Mk≤n），判定系统无故障。

将故障点标记为1，正常点标记为0，在处理正常点时，ACKF正常进行时间和量测更新。当检测到传感器故障时ACKF只进行时间更新不进行状态更新，来提高滤波算法的精度。

对于式(1)的非线性系统，基于马氏距离辅助自适应CKF算法主要计算过程如下：

步骤1 根据式(1)和式(4)建立多AUV协同定位状态空间模型；

步骤2 用CKF进行时间更新和量测更新；

步骤3 根据式(33)构造故障检测函数，利用新息序列马氏距离故障检测法对系统模型进行评估，并设定门限值；

步骤 4 根据式(30)构造自适应因子kη对协方差矩阵进行在线修正，提高CKF鲁棒性；

步骤 5 根据第三部分介绍的故障检测方法判断量测是否异常。若量测异常则标记为1，若量测正常则标记为0；

步骤6 当量测正常时，ACKF正常进行时间和量测更新。当检测到量测故障时，ACKF只进行时间更新不进行状态更新。

4 实验验证

4.1 实验情况描述

为了验证基于马氏距离辅助自适应CKF协同定位方法的有效性，用湖上试验数据进行仿真验证。实验使用三艘勘测船，其中两艘船安装高精度导航设备作为主AUV，另一艘安装低精度导航设备作为从AUV。主AUV和从AUV都配备了声学调制解调器ATM-885、多普勒速度计程仪和罗经；此外，从AUV还配备了全球定位系统（Global Positioning System,GPS），来提供参考位置，湖试设备如图1所示，所携带传感器信息如表1所示。

图1 湖试试验设备Fig.1 Lake test equipment

表1 传感器的性能参数Tab.1 Performance parameters of sensors

主AUV和从AUV的航行轨迹如图2所示。试验总时间为1700 s，采样时间1 s，GPS提供系统初始状态。在每一时刻，从AUV只与两艘主AUV中的一艘进行通信，从AUV通信周期为5 s，每个主AUV与从AUV的通信周期为10 s。以罗经提供的从AUV航向信息为基准航向，设置输入航向漂移误差为15°/h。初始状态估计误差协方差矩阵设为P0=diag[1m,1m]2，过程噪声协方差矩阵为Qk=diag[1m,1 m]2，测量噪声协方差为= [5m]2。

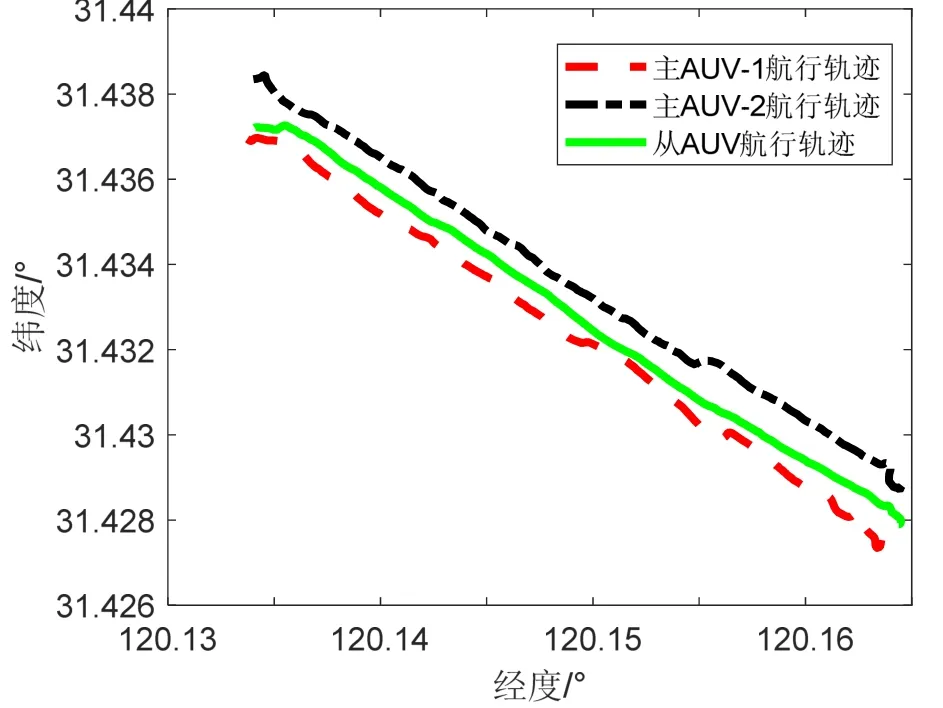
图2 主与从AUV真实轨迹Fig.2 The trajectory of piloting and following AUV

为了对比不同通信声呐测距误差下的协同定位性能，在本次湖试试验的基础上，增加了四种测距误差下的协同定位性能，还对比了出现野值时对CKF算法定位性能的影响。

由于本次湖试试验主AUV-1、主AUV-2和从AUV都配备有GPS作为基准，因此根据三个AUV的GPS数据所解算出来的距离，设置通信声呐距离精度分别为3 m、5 m、10 m、20 m时的量测数据，同时在通信声呐距离精度为5 m的量测数据上，增加本次湖试试验提取出来的野值点，并用CKF算法进行仿真结果如图3和表2所示。

表2 不同精度通信声呐协同定位性能Tab.2 Cooperative positioning performance of communication sonar with different precision

图3 不同精度通信声呐下，定位误差对比Fig.3 Comparison of position error under different precision communication sonar

由图3和表2可以得到，测距声呐精度越低，协同定位性能越差，其中野值噪声对协同定位性能影响尤其大，多AUV协同导航系统在航行时由于海洋复杂的环境，不可避免地会产生野值噪声。因此解决野值噪声对协同定位的影响是非常必要的。

在本次湖试试验中主AUV装配的声学设备每5 s发送一次信号，每次最多只有一个主AUV与从AUV进行通信。从AUV与主AUV-1和主AUV-2之间的量测信息如图4所示。

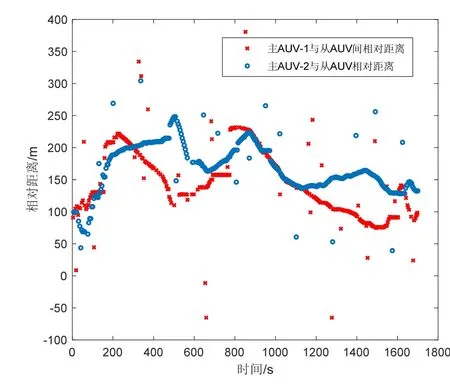
图4 主AUV与从AUV之间的量测距离Fig.4 Measurement distance between master AUV and slave AUV

由图4可以注意到，主AUV与从AUV之间的量测信息含有大量野值噪声，如果直接使用原始数据作为滤波的量测信息，相当于滤波器用错误的量测信息进行估计，对协同定位精度的影响很大，可能会导致位置估计误差发散。主AUV-1与从AUV之间的量测误差如图5所示。在接下来的实验中，本文将使用上述数据进行算法验证。通过图5可以发现，野值噪声往往偏差都很大，相比正常的量测数据，误差要大几十甚至上百倍，如果滤波器使用这种量测进行量测更新，会对估计误差产生很大影响。

图5 主AUV与从AUV量测误差及其概率分布图Fig.5 Master AUV and slave AUV measurement errors and their probability distribution

因此本文引入卡方检验来检测系统的不确定程度。将置信概率为99%对应的卡方检验值作为阈值。经计算，本文的卡方检验值设为6.635 m。若量测误差大于此阈值，则判定该量测为故障量测，并将其标记为故障点。若量测误差小于此阈值，则判定该量测有效，并将其标记为正常点。本文将故障点赋值为1，正常点赋值为0，方便后续算法的实现。卡方故障检验阈值及结果如图6所示。

图6 卡方故障检验阈值及结果Fig.6 Chi-square fault test threshold and results

本文将基于上述量测数据和卡方故检测结果进行相关算法的验证。首先在不进行故障检测时，只使用容积卡尔曼滤波算法与自适应容积卡尔曼滤波算法对从AUV的位置进行估计，从AUV轨迹和定位误差如图7和图8所示，在野值噪声较复杂的情况下，ACKF算法相比于CKF算法定位误差更小，也符合理论。但是在量测信息出现不更新等缓变故障时，例如100～200 s、700～800 s、1580～1615 s时，ACKF的定位误差也出现了明显增大。

本文所设计的基于马氏距离结合自适应容积卡尔曼滤波算法（MD-ACKF），利用故障检测出来的结果，在处理正常点时，ACKF正常进行时间和量测更新。当处理故障点时，ACKF只进行时间更新不进行状态更新，来提高滤波算法的精度，在短时间内ACKF只使用时间更新其误差不会发散太大，当量测信息正常后，其定位误差会继续收敛。

在声学测距异常条件下，基于马氏距离辅助自适应容积卡尔曼滤波算法结果如图7和图8所示，图7为不同定位方法估计得到的跟随AUV轨迹对比图。图8为不同定位方法估计位置与基准位置的距离误差。

图7 从艇轨迹对比图Fig.7 Comparison diagram from boat track

图8 定位误差对比图Fig.8 Comparison diagram of positioning error

由图7和图8可以看出，只利用航位推算算法得到的从艇轨迹与真实轨迹误差较大，且随时间发散，这是因为从艇的航位推算是由低精度的多普勒计程仪和船用罗经提供的新息解算的，导致定位误差会随着时间累计，航位推算轨迹会随着时间逐渐偏离从艇的真实位置，如果长时间只利用航位推算算法来进行导航定位，会导致轨迹漂移，产生严重后果。

本文分别使用了CKF、ACKF、残差卡方检测、马氏距离辅助容积卡尔曼滤波算法（MD-CKF）和马氏距离辅助自适应容积卡尔曼滤波算法（MD-ACKF）进行对比。由图7和图8可以看到，在100～200 s、700～800 s和1580～1615 s时间段内，量测出现严重异常时，如果不进行处理，其定位误差会明显增大，导致整个定位系统发散，甚至严重后果。本文所使用的基于马氏距离的自适应卡尔曼滤波算法可以有效解决由于量测异常导致的定位误差增大问题，对比多个算法结果表明，本文所提出的基于马氏距离的自适应卡尔曼滤波算法更稳定，精度更高，定位误差最大不超过15 m。

5 结 论

本文针对双艇交替领航协同导航系统传感器出现故障的情况，提出了一种基于马氏距离的自适应卡尔曼滤波算法，并通过湖试数据进行了仿真验证。主要内容如下：

(1)建立了多AUV协同定位算法的系统定位数学模型，提出了一种基于马氏距离的自适应卡尔曼滤波算法进行传感器故障诊断与处理，给出了该算法的详细过程。

(2)在协同定位系统传感器故障诊断基础上，对故障进行了有效处理，并通过湖试数据进行了仿真实验验证。

本文提出的基于马氏距离辅助的自适应容积卡尔曼滤波算法，将该算法故障诊断与容错结合，可以保证在水声设备出现故障情况下的多AUV协同定位精度，为多AUV协同定位系统的研究提供了思路。