基于SVM自适应零速检测的行人自主导航算法

纪志农，苗宏胜，李海军，孙 伟

（北京自动化控制设备研究所，北京 100074）

对于传统的行人导航方法，在有卫星信号时可依靠卫星提供定位导航和授时服务。但在室内、隧道等卫星信号无法到达或者被拒止的场景下，迫切需要行人导航系统具有不依赖卫星的自主定位导航能力[1]。基于微惯性测量单元（Miniature Inertial Measurement Unit, MIMU）的足绑式行人自主导航系统具有低成本、低功耗、体积小等优势，是目前的研究热点。

然而其核心部件微机电（Micro Electro Mechanical System, MEMS）惯性器件存在精度低、噪声大等问题，因此目前普遍采用零速修正（Zero Velocity Update,ZUPT）算法抑制航向、位置误差发散，以提高导航精度。由于ZUPT仅在零速区间对载体作滤波修正，因此零速检测的准确率直接决定了导航精度[2,4]。

为提高零速检测的准确率对复杂步态的适应性，戴洪德等提出一种基于伪标准差和N-P准则的行人导航零速检测算法[5]，该方法可在短距离、正常行走时实现较高的零速检测精度并提高适应性，但在大范围、长时间、高动态条件下适应性变差。贾铮洋等设计了混合运动模式下的双重阈值零速区间检测算法[6]，可在上、下楼梯时进行准确的零速检测，然而由于受阈值限制仍无法适应跑步状态。陈泽等设计了一种区间搜索零速检测器[7]，通过与J. Nillsson等设计的基于贝叶斯网络的零速检测器Adaptive-SHOE[8]进行对比，发现在跑步状态下Adaptive-SHOE失效[7]，区间搜索零速检测器精度更高。然而由于该方法以Adaptive-SHOE为基准，无法得到快速运动时的零速检测准确率，且在大动态运动时易出现局部失效的风险。综上，提高零速检测的准确率和适应性仍然存在较大的困难。

为解决该问题，本文提出了一种基于SVM自适应零速检测的行人自主导航算法。首先采用中值滤波（Median Filtering, MF）算法对MIMU采集的原始惯性数据进行降噪处理，由滤波窗口内三轴加速度矢量和的峰值判断当前步态，利用支持向量机（Support Vector Machine, SVM）对不同步态下零速点和非零速点的角速率、加速度的矢量和、标准差进行分类，进而提高零速检测对复杂步态的适应性，并通过ZUPT算法实现行人自主导航。

1 基于ZUPT的行人导航系统

1.1 行人导航系统设计

基于ZUPT的行人自主导航系统流程图如图1所示。首先由足绑式MIMU采集人体运动时足部的角速率和加速度，经中值滤波预处理后进行导航解算。同时检测当前是否为零速状态，若判断当前为零速状态，则通过卡尔曼滤波（Kalman Filtering, KF）对当前足部的姿态、速度、位置误差进行估计，并进行修正，便可得到行人当前的准确位置[2,3]；若判断当前为非零速状态，则不作修正，以惯性导航解算结果作为导航数据。

图1 基于ZUPT的行人自主导航流程Fig.1 The process of pedestrian autonomous navigation based on ZUPT

由于人在行走过程中，在非零速时刻，以足部速度为0作为观测量对姿态、速度、位置误差进行修正会使导航结果产生较大谬误，因此只能在零速时刻对姿态、速度、位置误差进行修正，而其余时刻则不做修正。因此，能否准确检测出当前是否为零速状态，直接影响到行人导航的精度。

1.2 零速检测算法

人在行走的过程中，每个步态周期可分为4个阶段：离地、悬空摆动、落地、持续静止[9,10]，如图2所示。

图2 单个完整步态周期Fig.2 A complete gait cycle

对于任意一只脚来说，在一个步态周期内，有一半左右的时间是静止的，此时足部的速度为0，即零速状态，这段时间即为零速区间，零速区间内的任一时刻为零速时刻[1]。目前常用的零速判据包括加速度阈值检测[11]、角速率阈值检测[11]、加速度标准差检测[2]、角速率标准差检测[2]等。

（1）加速度、角速率阈值检测

若三轴加速度、角速度的矢量和分别满足：

则判断当前为零速状态。其中fx(k)、fy(k)、fz(k)分别为k时刻MIMU输出的三轴加速度，ωx(k)、ωy(k)、ωz(k)分别为三轴角速率，分别为三轴加速度、角速率矢量和，g为重力加速度，fth、ωth分别为加速度、角速率的零速检测阈值。

（2）加速度、角速率标准差检测

若三轴加速度、角速率的标准差分别满足：

则判断当前为零速状态。其中σf(k)、σω(k)分别为k时刻MIMU输出的单轴加速度、角速率的标准差，fk、ωk分别为单轴加速度、角速率，、分别为窗口内加速度、角速率的平均值，N为窗口宽度，σfth、σωth分别为单轴加速度、角速率的标准差阈值。

由于MIMU自身存在一定误差，且不同人的行走习惯也不同，单一的零速判据很容易造成大量的误判（非零速状态被判为零速状态）和漏判（零速状态被判为非零速状态），因此目前常采用多条件零速区间判别方法，即判断当前MIMU输出同时满足多条判据才认为当前是零速状态[12]。

上述各判据的阈值fth、ωth、σfth、σωth等常采用经多次试验确定的常数，即得到了固定阈值零速检测法，对于固定人员的固定步态（如正常行走）可以实现较高的准确率。然而，当试验人员、步态发生变化（如快跑、慢跑等）时，仍存在大量误判和漏判的现象。

可将不同步态划分为不同的区间，在不同区间内对零速检测阈值fth、ωth、σfth、σωth分别进行调整，即分别对正常行走、慢跑、快跑等步态设置不同的阈值，以实现零速检测算法对不同步态的适应性，即得到了自适应阈值零速检测法。然而在不同区间内，该方法各阈值依然为常数，虽然在高动态运动时相较于固定阈值零速检测法可获得更高的零速检测准确率，但仍会存在少量漏判、误判的现象。

1.3 滤波器设计

卡尔曼滤波（KF）是一种通过线性化系统的观测量，对系统状态进行最优估计的算法[3]。线性化后行人自主导航系统的状态空间模型可表示为：

其中X(t)为状态变量，F(t)为系统矩阵，Z(t)为量测量，H(t)为量测矩阵，w(t)为系统噪声向量，v(t)为量测噪声向量。取状态变量：

其中，Vδn、Vδu、Vδe分别为系统北向、天向、东向的速度误差；Lδ、hδ、δλ分别为系统的纬度、高度、经度的误差；φn、φu、φe分别为系统导航坐标系内北、天、东三个方向的失准角；∇x、∇y、∇z分别为系统载体坐标系内x、y、z三个方向的加速度计零偏；εx、εy、εz分别为载体坐标系内x、y、z三个方向的陀螺漂移。

量测量：

其中Vn、Vu、Ve分别为系统北向、天向和东向惯性导航的速度；Vnbase、Vubase、Vebase分别为系统中可作为基准的北向、天向和东向的速度，在零速时刻有：

量测矩阵：

标准KF方程如下[3]：

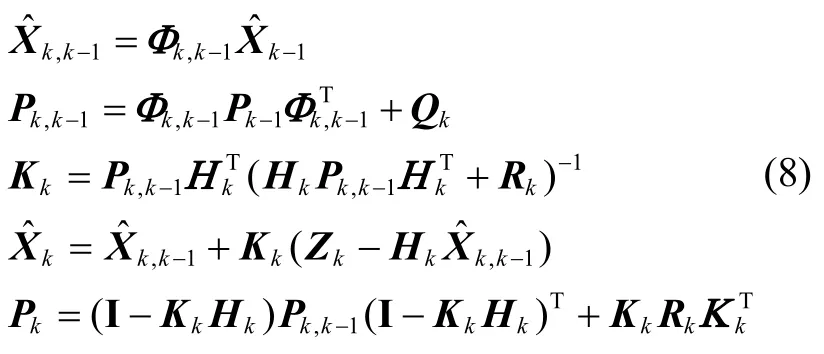
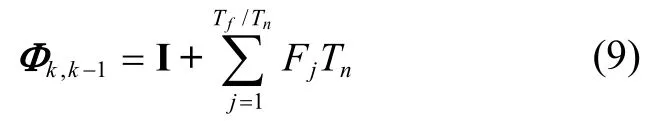
其中，Tf为KF滤波周期，Tn为导航周期[3]。

由KF估计出各状态变量的误差后，对各状态变量进行修正。由于ZUPT算法的固有缺陷，KF无法对航向角进行准确估计，且对三轴加速度计零偏、三轴陀螺漂移的估计周期较长，因此仅对系统的北向、天向、东向速度，俯仰角，滚动角进行修正。且由于仅在零速区间存在= 0，因此仅在零速区间对行人的姿态及速度进行修正，其余时刻则不作修正。

2 基于SVM的自适应零速检测算法

2.1 惯性数据预处理

由于人在行走时，足部运动具有幅度大、冲击大等特点，因此足绑式MIMU采集的原始惯性数据会存在大量的脉冲干扰和随机噪声，会降低零速检测的准确度。本文采用中值滤波算法对MIMU原始数据进行预处理，其具体流程如下[11,13]：

（1）对当前时刻点所在滑动窗口内的数据点进行遍历；

（2）将所有数据从小到大排列；

（3）求取序列中点的中位数；

（4）用求取的中位数替代该时刻原始的数值。

经中值滤波后，MIMU原始数据中的高频噪声信号得以滤除，且保留了零速点原有的数据特征，可有效减少脉冲干扰和随机噪声对零速检测的干扰[11,13]。下文所提到的角速率、加速度均为中值滤波后的数据。

2.2 步态的表征

统计正常行走、慢跑、快跑时MIMU输出加速度峰值的变化范围、零速区间内加速度和角速率的均值，结果见表1。由表1得随着运动速度的加快，零速和非零速状态下加速度、角速度的矢量和均增大，此时固定阈值判据显然已不再适用。而其中加速度的变化较为明显：随着运动速度的加快，足部需要以更快的速度运动，而步态周期又会进一步缩短，因此在步态周期的非零速区间内足部加速度的峰值会增大。因此，可以采用任意时刻所在滑窗内加速度矢量和的峰值来对当前的运动状态进行表征。

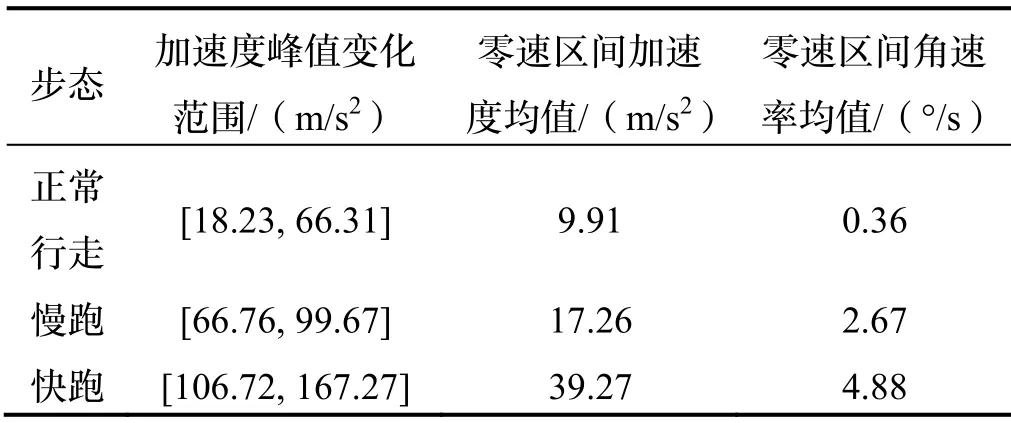
表1 不同步态足绑式MIMU输出数据Tab.1 The output of foot-mounted MIMU for different gaits

2.3 基于SVM的零速检测判据

SVM是一种用于解决二分类问题的机器学习方法，其基本原理为通过机器学习，在空间中找到一个最优超平面，使不同类型的点间的几何间隔最大[14,15]。基于SVM的自适应零速检测算法的具体实现过程如下：

（1）构造样本数据集

将一套MIMU设备绑在一只脚上，采集多组不同人员包含多种不同步态的数据，并将其汇总，挑选出其中特征明显的零速点和非零速点。目前基于SVM的零速检测与行人导航普遍将样本数据集构造为如下形式[14]：

其中n为样本容量；zi=-1或1，表示当前的足部运动状态，zi= 1表示该点为零速点，zi=-1表示该点为非零速点。这样虽然可以对零速点和非零速点进行分类，然而由于未考虑不同步态的情况，导致在行人快速运动时分界面失效，且样本类型单一，从而使零速检测准确率变差。本文将各点的分别与σfx、σfy、σfz、σωx、σωy、σωz构成二维数组作为SVM的样本训练集，可实现对不同步态下零速点和非零速点的上述参数进行分类，提高零速检测对不同步态的适应性。构造的多组训练样本数据集形式如下：

其中y表示σωy、σωz等参数。

（2）求解最优超平面

由于行人行走的样本数据并不是线性可分的，因此需要先将样本点通过映射关系转换到高维空间使其线性可分。此时所求解最优超平面的模型为：

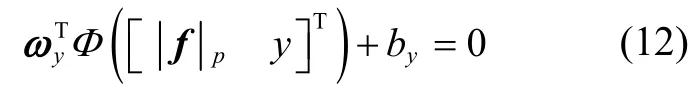
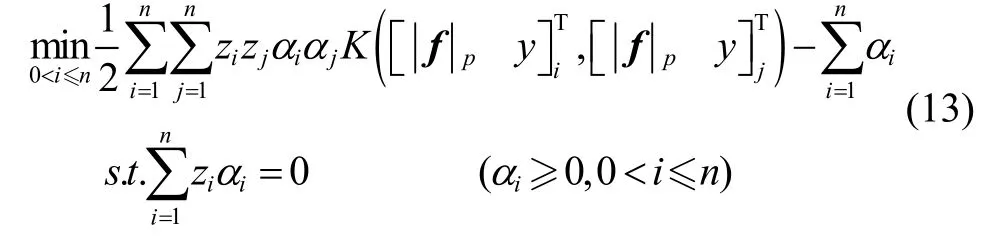
其中

就可以将两种状态很好分开。而在复杂步态下，线性的分界面已不能将两种状态分开，因此需考虑更换核函数。由于高斯核对于各种类型的样本都有较好的性能，且所需参数较少，因此在缺乏先验信息的情况下选择采用高斯核函数来对式(13)进行求解。取

（3）构造决策函数

根据式(12)(17)构造决策函数：

对于第j个样本点，若为正，则认为该点为零速点，否则认为该点为非零速点，由此实现对所有零速点和非零速点的分类。

采用SVM算法对所采集的所有的样本集中的样本点进行分类。不同样本集的分类结果如图3所示。图3中各曲线即为基于SVM得到的零速点和非零速点的边界在图示平面内的投影。经过样本集的多次扩充后，发现该最优超平面的形状呈现出大致确定的趋势，此时的决策函数即可作为成熟的零速检测判据。

图3 不同样本集的SVM分类结果Fig.3 The result classified by SVM for different sample sets

然而由于单一判据错判率较高，导致一些非零速点出现在边界零速区域，而部分零速点出现在非零速区域，这些点分别对应着误判和漏判。由第1节可得，若发生误判，会使KF的量测量出现错误，导致导航结果向错误的方向修正，引起导航误差，并影响后续导航解算；而发生漏判，则会以惯性导航数据作为当前零速点的导航参数，而在后续的零速点被修正回来，不会影响后续导航。因此需优先考虑去除误判点。

通过统计发现大部分的误判点仅能使个别参数y满足零速条件，即仅会在个别图中出现在非零速区域，因此可通过对其他判据进行判断来淘汰这些误判点。只有所有参数y同时满足零速条件，才认为当前为零速状态。又通过后续的试验和仿真，发现所有错判点中误判点的概率要远大于漏判点。该条件所导致的漏判可忽略不计。

3 试验验证

3.1 试验内容

将一套行人导航系统固定在一只脚上，使MIMU的x轴与人体行进方向一致，y轴指天，z轴与人体行进方向垂直并指向行进方向的右侧。在系统开始工作前，将MIMU紧靠在基准面上，使系统工作后保持某一固定初始航向约5 min，然后开始行走。在行走时随机加入多种特殊步态，如快跑、慢跑等，并保证行走过程中部分路段被重复行走至少2次，以便对比2次经该路段时的位置。行走30 min左右后回到出发点，重新将MIMU靠在基准面上使系统位置、航向与初始时刻相同。分别由3位试验人员重复上述过程各5次，用于后续统计。

分别采用基于SVM的自适应零速检测法（SVM自适应检测法）、固定阈值零速检测法（固定阈值法）、自适应阈值零速检测法（自适应阈值法）对足绑式MIMU采集的数据进行零速检测，并进行导航解算。其中三种零速检测方法的判据均在试验前确定，新采集的数据可在试验结束后作为样本点对样本集进行扩充。

3.2 零速检测结果

为防止由其他零速检测算法的结果作为基准而引起误差的累加，提升零速检测准确率的可信度，本文采用对MIMU的输出进行人工判别来得到零速检测结果的基准。由于多次试验得到的数据量太过庞大，因此本文截取多组不同步态下零速特征明显的行人行走的片段作为样本来进行人工判别。以样本的各帧数据的人工判别结果构造序列(i= 1,2,...)作为基准，其中i为帧号，=0或1。若=1则该帧为零速状态，= 0表示该帧为非零速状态。再分别采用SVM自适应检测法、固定阈值法和自适应阈值法对采集到的惯性数据进行零速检测，分别得到零速检测的结果序列Li,1、Li,2和Li,3。将Li,1、Li,2、Li,3分别与作对比，计算：

若 ΔLi,j= 0，则该帧零速检测结果正确；若ΔLi,j= 1，则该帧发生了误判；若 ΔLi,j=-1，则该帧发生了漏判。按照不同步态对ΔLi,j及分段，分别统计3种方法不同步态下零速检测算法的准确率、误检率和漏检率。取零速检测准确率的最小值作为该方法的准确率，统计结果见表2。

由表2得，在正常行走时，三种零速检测算法的准确率均能达到99%以上，且均维持在较高水平。然而随着行走速度的加快，采用固定阈值法和自适应阈值法的零速检测准确率显著下滑，分别降至51.4%和91.5%；而SVM自适应检测法的准确率虽有下降却仍能达到97.2%，维持在95%以上，说明SVM自适应检测法较固定阈值法及常用自适应检测法具有更高的准确率，对不同步态的适应能力更强。

表2 不同零速检测算法的准确率Tab.2 The accuracy of zero-speed detection for different zero-speed detection algorithms

3.3 行人导航结果

采用全球卫星导航系统（Global Navigation Satellite System, GNSS）对起始点及转弯处的经纬度进行多次测量，得到其准确位置，作为定位误差计算的基准点。分别采用3种零速检测算法对实际采集的MIMU数据进行仿真，求仿真得到的导航轨迹各转弯处的位置与基准点位置间的相对距离，即为各转弯处的定位误差。取单条轨迹定位误差的最大值作为该条次的定位误差。仿真得部分轨迹及基准点位置如图4所示。

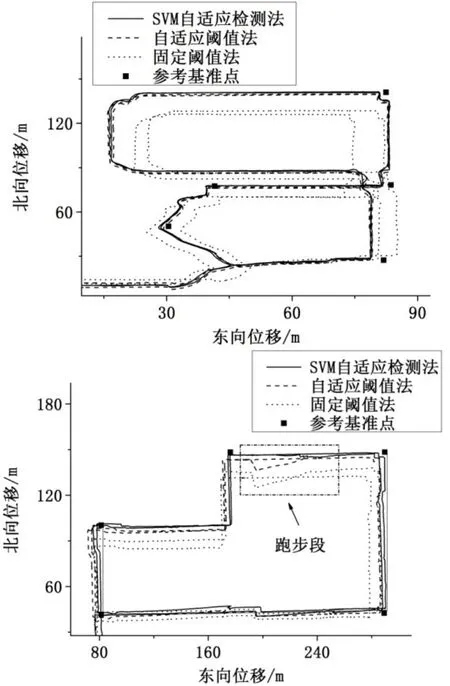
图4 采用不同零速检测算法时的部分导航轨迹Fig.4 Fragments of the navigation trajectories when using different zero-velocity detection algorithms

由图4可得，采用SVM自适应检测法时转弯处与基准点的重合度要高于自适应阈值法，且明显高于固定阈值法。图中方框内为跑步时的轨迹，实际轨迹为直线。可以观察到采用固定阈值法时轨迹发生严重偏移，这是由于该段轨迹固定阈值法无法判断出零速状态，未进行零速修正造成的；相较于采用固定阈值法，采用自适应阈值法时由于判别出部分零速区间，故轨迹有所修正，然而错判现象仍然存在，轨迹仍然存在较大误差；而采用SVM自适应检测法时，由于该段大部分零速状态均能被判断出来，因此轨迹可被多次修正，因此其偏移更小。

采用不同零速检测算法后计算得定位误差的统计结果见表3。

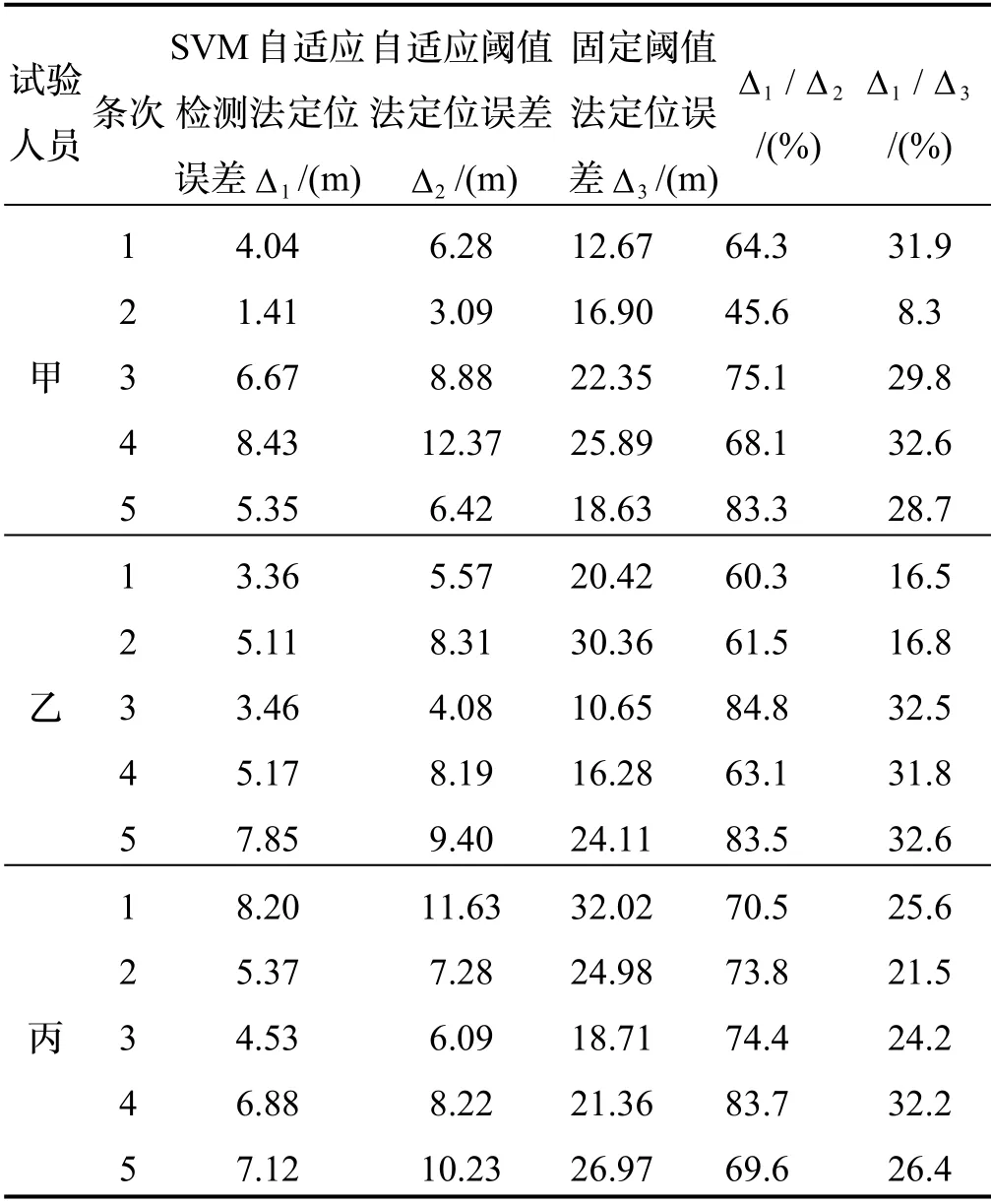
表3 基于不同零速检测算法的定位误差Tab.3 The positioning error based on different zero-speed detection algorithms

由表3得，在其他条件完全相同的情况下，在30 min内，采用自适应阈值法及固定阈值法时的最大定位误差为12.37 m和32.02 m，而采用SVM自适应检测法时的最大定位误差为8.43 m。采用SVM自适应检测法与采用自适应阈值法时系统的定位误差之比为60.3%到84.8%，与采用固定阈值法时系统的定位误差之比为8.3%至32.6%，即采用SVM自适应检测法时系统的定位精度比采用自适应阈值法时提高15.2%以上，比采用固定阈值法时提高67.4%以上。说明采用SVM自适应检测法时的导航精度要远高于采用自适应阈值法和固定阈值法的导航精度。

此外，相较于自适应阈值法中判据需根据试验反复调整，SVM自适应检测法更易于获取稳定的零速判据，具有更大的优势。

4 结 论

本文通过对经中值滤波预处理的足绑式MIMU输出数据进行分析，选择以某一时刻所在滑窗内加速度矢量和的峰值来划分该时刻步态。采集多种不同步态下足部角速率、加速度的原始数据，以不同和其对应的三轴加速度、角速率的矢量和、标准差等分别作为训练样本集，采用SVM算法实现对零速点和非零速点的自适应划分。若某一时刻三轴加速度矢量和、角速率的矢量和、标准差等均落在零速区域，则认为该时刻为零速状态。

经试验验证，在正常行走时，基于SVM的自适应零速检测算法和固定阈值零速检测算法的零速检测准确率均能达到一个较高的水平；而跑步时采用SVM自适应检测法的准确率达到97.2%，高于采用自适应阈值法时的91.5%，且远高于采用固定阈值法时的51.4%，说明SVM自适应检测法对复杂步态具有更高的准确率和更强的适应性；采用SVM自适应检测法时系统的定位误差降至采用自适应阈值法时的84.8%以下、采用固定阈值法时的32.6%以下，即系统导航精度较采用自适应阈值法时至少提升了15.2%、较采用固定阈值法时至少提升了67.4%。说明采用SVM自适应检测法时可获得更高的导航精度。基于SVM自适应零速检测的行人自主导航算法可提升系统对复杂步态的适应性，进而提高系统导航精度，具有一定的实际应用价值。