基于细观模型的泵送混凝土温度场演化机理研究

程 井 李明志 王雪丰 张 鹏 蒋子涵

(1.河海大学 水利水电学院, 南京 210098;2.上海市堤防(泵闸)设施管理处, 上海 200080)

目前高性能泵送混凝土已被广泛应用在泵闸等水工建筑物之中,其具有碎石粒径较小、胶凝材料用量大、绝热温升值较高等特点[1-2].早龄期凝土内部温度场不断发生变化,泵站流道、水闸墩墙等重要结构在边界约束作用下易产生裂缝,影响结构的耐久性[3].在细观尺度上准确预测混凝土温度场及判断其影响因素是温控防裂关键的一步.Kim K H 等[4]通过试验研究了多种细观组分变量对混凝土导热性能的影响,提出了混凝土导热系数的预测方程;Demirboga R 等[5]通过试验,对比分析了不同胶凝材料用量及其组分对混凝土导热系数的影响;宋智通等[6]通过细观二相模型将水泥水化程度的函数应用在混凝土绝热温升预测模型上;王立成等[7-8]提出了适用于热量传输分析的细观格构网络模型来模拟混凝土绝热温升变化规律;杜修力[9]等在损伤细观模型的基础上研究了混凝土的导热性.以上试验研究工作量大,且在宏观尺度上不能描述各细观组分对混凝土内部温度场分布的影响;数值分析方面的研究都是基于理想圆形骨料及混凝土的绝热温升值开展的,而非在细观层次上考虑骨料的真实性、离散性、随机性及砂浆的真实水化放热.

本文基于蒙特卡罗随机投放算法建立泵送混凝土的三相细观数值模型(碎石骨料、砂浆及界面过渡层(简称ITZ)).根据室内绝热温升试验及所用材料的配合比换算出砂浆放热量并计算出其作用于整体试件的温升值;运用与试验结果吻合良好的基于水化度的指数双曲线型绝热温升模型对细观泵送混凝土温度场进行分析,探讨了骨料的形状、离散性、骨料体积分数(体现胶凝材料用量)及在细观层次上采取温控措施对温度场的影响.

1 计算原理与方法

1.1 碎石骨料的随机生成与投放

Walraven J C在Fuller W B提出的最理想的三维级配曲线的基础上建立了混凝土试件骨料二维截面面积与骨料空间级配及含量的关系式,把混凝土细观结构数值分析的三维空间问题转化为了二维平面问题,极大提升了计算效率.混凝土试件二维截面上任一点骨料颗粒粒径R小于筛孔径R0的概率为[10]:

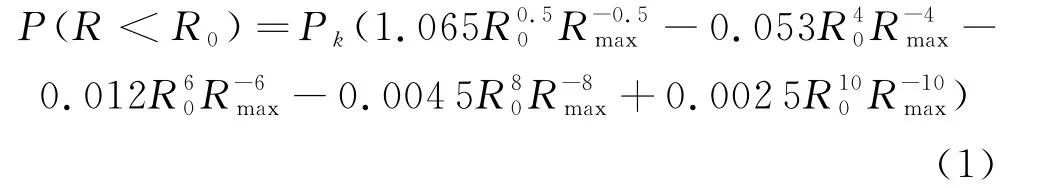
式中:R0为骨料筛孔孔径;Rmax为最大骨料直径;P k为骨料(包括粗骨料和细骨料)占混凝土总体积的百分比.

混凝土试件中的粗骨料实际形状为不规则的凸多面体,为更真实地模拟混凝土细部结构,在混凝土试件二维截面上需要用4～12边的凸多边形来模拟碎石骨料.由于凸多边形碎石骨料的面积可以等效成圆形骨料的面积[11],所以Walraven公式也适用于确定碎石骨料的面积.

碎石骨料随机投放算法的步骤为:

1)应用Walraven公式确定出碎石骨料随机投放算法的控制参数,即碎石骨料的数量或碎石骨料总截面积.

2)生成凸多边形的基础骨料.为了确保基础骨料形状为凸多边形,采取在圆内随机取n个点,n=round[A+rand(1)×(N e-3)],其中A和N e都为碎石骨料边数的控制参数,ang=rand(1,n)×360,将n个ang角度进行排序和编号,本文算法在任志刚[10]对多边形基础骨料算法的基础上增加了最大角度angmax和最小角度angmin的控制条件,避免了碎石基础骨料为片状或针状的情况.

3)碎石基础骨料的延拓与凸性判断.以N边形基础骨料的最长边进行延拓,新生成延拓点p的坐标为:

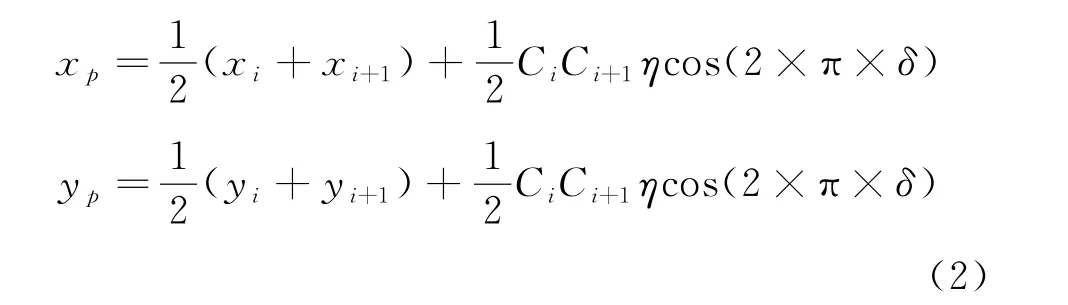
式中:Ci C i+1为基础骨料最大的边长;(x i,y i)为C i点的坐标;(x i+1,y i+1)为Ci+1点的坐标;η和δ为(0,1)内的随机数.为了保证延拓后的多边形为凸性,p点需要落在C iC i+1的外部半圆内,判断条件为p点与C iC i+1及相邻两边C iC i-1、C i+1C i+2按顺时针方向构成的三角形的面积S Ci(S Ci＞0)满足式(3):

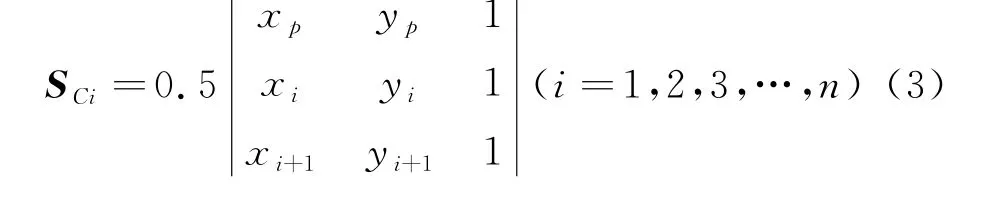
4)延拓点侵入多边形的判断.设p点与多边形每条边两端点组成的三角形的面积为S Ci(i=1,2,3,…,n).判断准则:任意S Ci＞0,点侵入多边形骨料内部;至少一个S Ci=0,点在多边形骨料边界上;至少一个S Ci＜0,点不侵入多边形骨料.

5)判断延拓后多边形骨料面积是否在与之对应圆骨料面积的预设范围内,否则继续步骤3),若满足条件,存储碎石骨料信息.

1.2 基于水化度的混凝土绝热温升模型

1.2.1 等效龄期与水化度

水泥水化反应过程放出的热量会使早龄期混凝土内部温度升高,混凝土温度的升高又会对实际水化放热反应造成一定的影响,水泥水化反应速率随着温度的升高会逐渐加快,为了排除不同的水化温度对于水泥水化过程的影响,Erik Pedersen和Hansen[12]在Arrhenius函数的基础上提出积分形式的等效龄期成熟度函数:

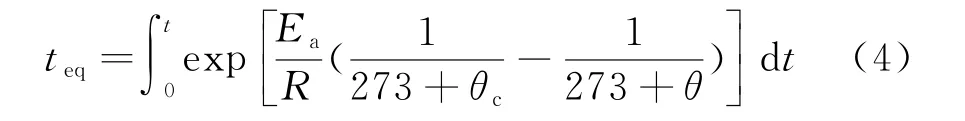
式中:teq为等效龄期成熟度;Ea为混凝土活化能(J/mol);R为气体常数[J/(mol·K)];θc为混凝土的参考温度(℃);θ为Δθ内混凝土的平均温度(℃).

式(4)可以在水泥水化反应的过程中考虑不同水化温度对于水化放热的影响,把在水化环境温度T下进行水化反应时间t,转换为在参考温度θc下进行水化反应时间teq.水化度通常与混凝土的等效龄期成熟度teq紧密联系,它表示在某一时刻水泥水化反应的程度与胶凝材料在完全水化程度时的比值[13],在绝热温升试验下公式可表示为:

式中:β(τ)为在τ时刻水泥的水化反应程度;Dhr(τ)为在τ时刻时累积参加水化反应的胶凝材料量(kg);Duhr为完全水化反应时胶凝材料的总量(kg).

根据现有的研究成果[13],基于等效龄期的水化度的关系式可以表示为:

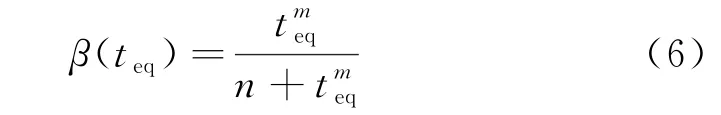
式中:n为曲线形状参数,常数;m为曲线坡度参数,常数;teq为等效龄期成熟度,常数.

1.2.2 基于水化度的指数双曲线型绝热温升模型

在试验基础上得到的指数双曲线型绝热温升计算模型公式为:

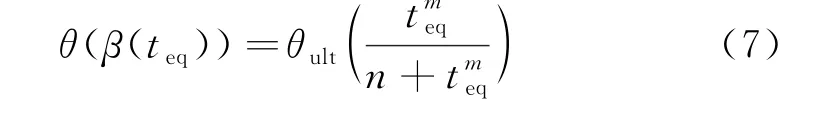
式中:θ[β(teq)]为基于水化度的混凝土的绝热温升(℃);θult为混凝土的最终绝热温升(℃).

水泥的水化反应是一个比较复杂的动态过程,基于水化度的指数双曲线绝热温升计算模型不仅考虑了龄期对于水泥水化放热的影响,而且考虑了混凝土自身温度变化的影响,更加真实地模拟了水泥水化的放热过程以及提高了混凝土内部温度场数值分析的可靠度.

1.3 基于细观结构的砂浆水化放热模型

在混凝土细观结构的三相材料(骨料、ITZ 及砂浆[14])中,仅考虑砂浆的放热作用,然而现在研究中主要采用混凝土的绝热温升值来计算,为了使混凝土细观结构内部温度场的演化更为精确,将式(8)水泥水化热与混凝土绝热温升的关系[15]换算为砂浆的水化热.

在混凝土绝热温升试验(如图2所示)中,试件采用P.O.42.5的普通硅酸盐水泥,碎石为5～25 mm的连续粒级骨料,P2a=30%(试件截面中骨料截面积与整个试件截面积的占比用P2a来表示),试验泵送混凝土配合比见表1.由绝热温升试验得到混凝土的最终绝热温升值为49.5℃.

表1 试验泵送混凝土配合比 (单位:kg/m3)

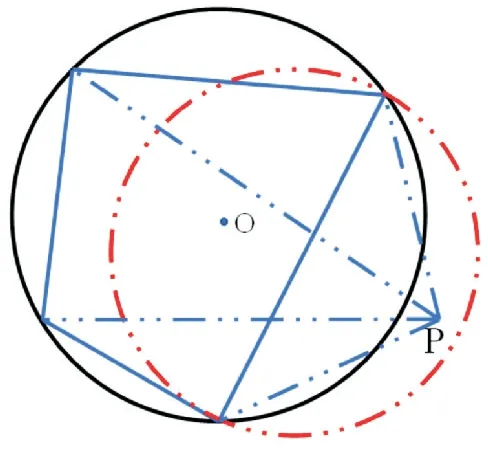
图1 基础碎石骨料延拓

图2 室内绝热温升试验

根据混凝土的最终绝热温升值及配合比,由式(8)反推得到水泥水化热Qce为376 kJ/kg.砂浆的用量为水的用量Mw、水泥的用量Mce、混合材料用量Mmix及砂的用量Ms之和.考虑砂浆的水化热全部作用于混凝土试件的温升,最大温升θult为式(9),计算出θult=72.32℃.

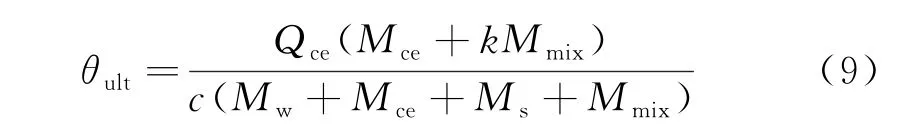
式中:c为砂浆的比热容,取1.175 k J/(kg·℃).

采用式(10)对P2a=30%的混凝土试件进行数值计算,其最高温度及中心温度结果与室内绝热温升试验结果对比如图3所示.

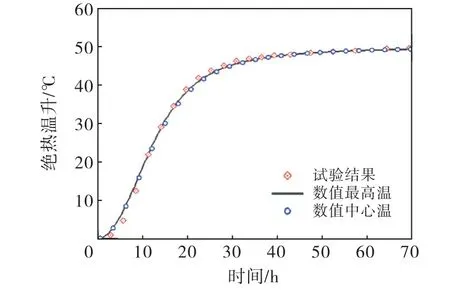
图3 混凝土试件的绝热温升过程线

结果表明,数值计算结果与室内试验结果吻合良好,温升阶段产生误差的主要原因在于碎石骨料的不均匀分布导致试件内部的各个局部区域中砂浆的质量分数不同(体现胶凝材料的用量不同),进而导致各局部区域前期温升速率不同.

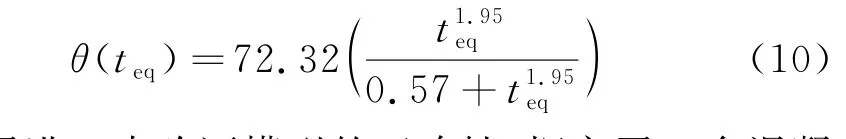
为了进一步验证模型的正确性,探究了5个混凝土初始浇筑温度(10、15、20、25、30℃)对于试件最大绝热温升过程线的影响,由绝热温升对比曲线(如图4所示)可以看到当混凝土的初始温度由10℃提升到30℃时,试件内部温升增量达到45℃所需要的时间提前了11.5 h,可见混凝土不同的初始温度对绝热温升过程的影响比较大,但在同一P2a下,最终绝热温升值以及绝热温升曲线前期迅速抬升,后期逐渐趋于稳定的这个趋势不会因混凝土初始温度的不同而变化.因此,在细观尺度上仅考虑砂浆的水化放热作用并运用基于水化度的指数双曲线型绝热温升模型可以较为准确地预测泵送混凝土试件内部温度场的演化过程.

2 泵送混凝土内部温度场的影响因素

在细观尺度上,骨料作为泵送混凝土试件的一个重要组成成分,其热学性能与另外两相材料相比差异较大并且在相同尺寸的试件中骨料的体积分数与砂浆的质量分数(体现胶凝材料用量)成反比.因此研究了骨料形状、骨料的体积分数、在P2a=25%条件下骨料粒径和数量及采取骨料预冷措施对于泵送混凝土早期内部温度场的影响.

计算模型的边界条件全部为绝热状态,初始浇筑温度为25℃,细观三相材料的物理参数见表2.ITZ的物理参数难以直接测量,且受砂浆及骨料特性、养护龄期及饱和度的影响较大.本文参考文献[16],假定孔隙体积分数为50%,砂浆及粗骨料体积分数均为25%,并取饱和度为50%,此时可得到相应的导热系数、密度及比热容的近似值.

2.1 骨料形状对温度场的影响

为探究骨料形状对于温度场的影响,模型采用60 mm×60 mm 的混凝土试件截面模型,内部圆形、椭圆形以及碎石单骨料的P2a均为30%(如图5所示).选取几个不同时间段的温度云图(如图6所示)进行对比可以看出,不同骨料形状的混凝土试件在不同时间段都在骨料周边产生了类环状的温度梯度,温度从骨料中心向外围逐渐升高;在相同时间段对比,发现(a)(圆形骨料)、(b)(椭圆骨料)和(c)(碎石骨料)图的温度梯度最大温差ΔT≤0.1℃,温度梯度基本相同.因此骨料形状的差异对于混凝土试件内部温度场的影响可以忽略不计.

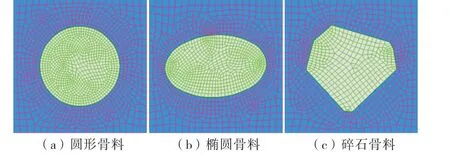
图5 P 2a=30%时不同形状的骨料模型

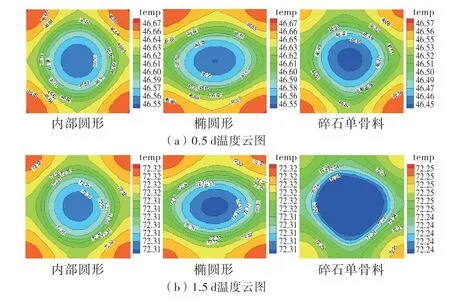
图6 不同时间段温度云图

2.2 不同骨料体积分数对内部温度场的影响

为更好地研究骨料体积分数对于泵送混凝土内部温度场的影响,数值模型采用与绝热温升试验相同大小的截面(400 mm×400 mm),将P2a=0%(纯砂浆)时的模型设置为对照组,对比分析了P2a在20%、25%、30%和35%情况下泵送混凝土试件内部温度场的计算结果.

图7 不同P 2a 试件模型图

通过研究在不同P2a下混凝土试件内部温度场的计算结果(图8～11)可以发现:

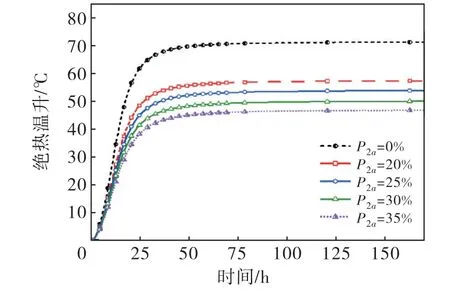
图8 不同P 2a 试件绝热温升对比

1)当P2a由0%增加到35%时,前期绝热温升速率逐渐降低,且最终温升值也逐渐降低,P2a=35%时内部温升增量达到40℃的时间相比对照组延迟了14 h,最终温升值也下降了近24℃.

2)在相同P2a下,对两组试件进行了分析(b组相对a组的骨料数量多、粒径小),试件内部温度场实际分布情况会因随机碎石骨料粒径和数量的不同而发生改变,但对最大温升θult和温升过程没有较大的影响.

3)设R n为试件内部温差与平均温度的比值,该值用来描述内部温度分布的均匀情况.当P2a＞25%时,在任一相同时间段的内部温差值随着P2a的增加而减小;最大内部温差产生的时间段为0.6 d左右,之后随着水化反应的进行,R n值逐渐降低,当水化反应进行到第1天时,内部温度基本一致.

4)在骨料随机投放及内部各相材料热学性能差异的影响下,等温线在骨料附近受到扰动并且在骨料密集的地方呈现出不规则的包围状低温区,随着水化反应速率的降低,等温线逐渐趋于平顺.

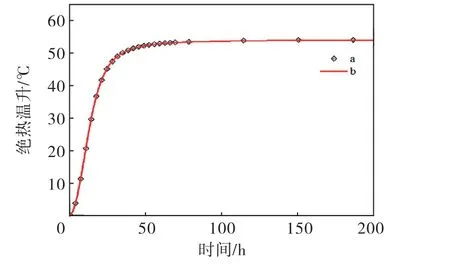
图9 相同P 2a 下骨料粒径和数量对绝热温升过程的影响

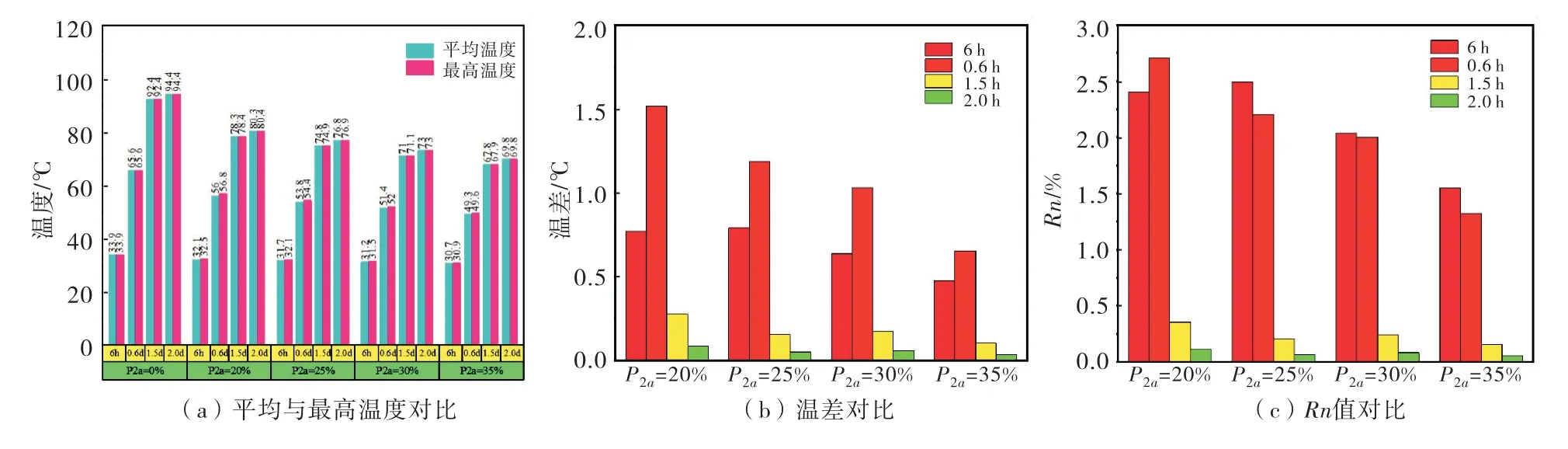
图10 不同P 2a 试件内部温度对比

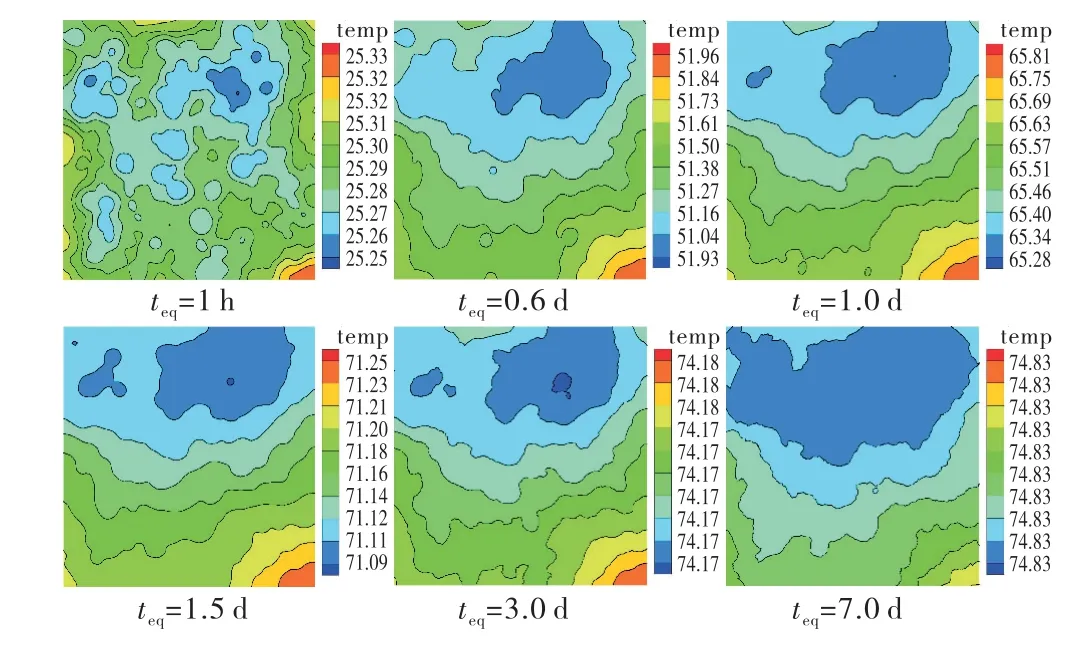
图11 P 2a=30%试件内部温度云图

可见,不同骨料的体积分数对泵送混凝土早期内部温度场的影响较大.产生以上现象主要有两个原因,一方面骨料在混凝土内部并不会发热,在砂浆水化放热的过程中,因骨料导热系数大,会从其中吸收大部分热量来提升自身温度,当骨料体积分数减少时,砂浆的质量分数增加(胶凝材料用量增加),放热量也相应增加,提高了混凝土内部的温度;另一方面随着混凝土内部温度的升高,又会加快砂浆的水化放热速率.

2.3 采取骨料预冷措施对泵送混凝土内部温度场的影响

高温季节浇筑泵送混凝土时,事先将骨料进行冷却处理,将混凝土内部的温度控制在合理的范围之内,防止温度裂缝的产生.因此从混凝土细观结构的角度去研究骨料预冷措施对于内部温度场的影响十分必要.在绝热条件下,P2a=30%,砂浆的浇筑温度为25℃,对骨料分别冷却到5、10和15℃.选取试件内部两个骨料中心点O1、O2以及3条y轴特征线对采取骨料预冷措施进行分析,如图12～14所示.

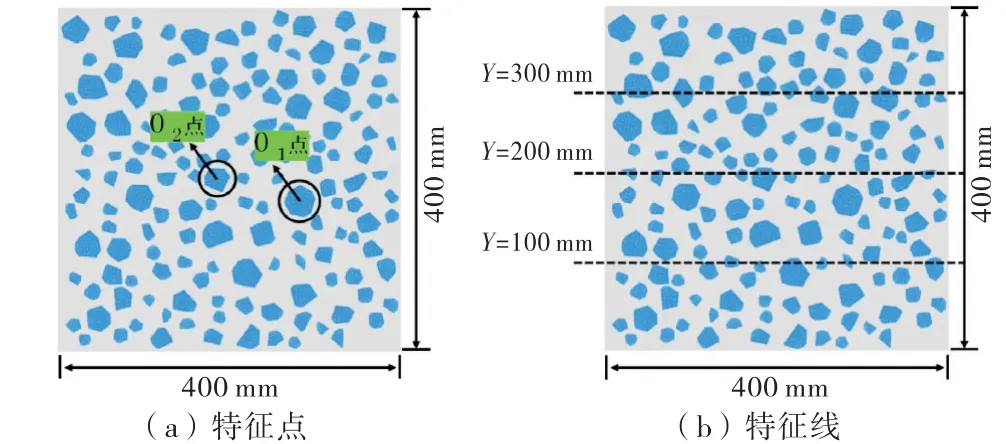
图12 试件特征点及特征线图

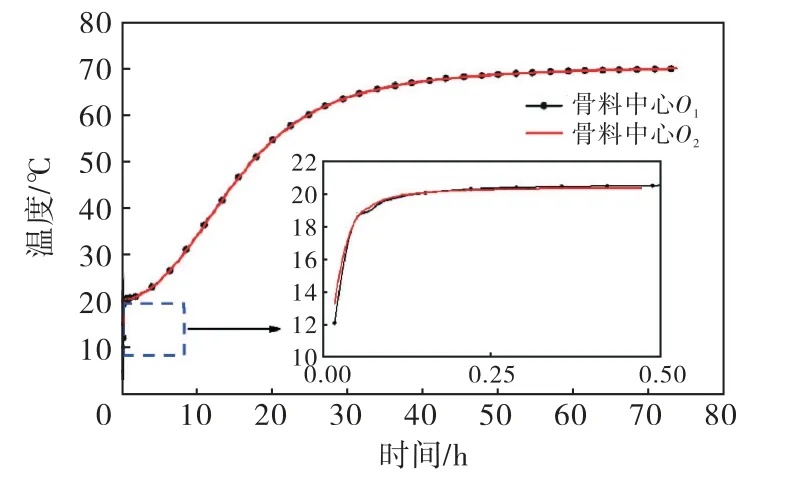
图13 骨料中心点温度历程曲线

通过观察骨料预冷温度为10℃时混凝土内部骨料特征点及特征线(y=100、200、300 和200 mm 处骨料的不同预冷温度)的温度结果可以发现:

1)由于骨料的导热系数较大,在前期较短的时间内,骨料吸收大量砂浆水化放出的热量,使温度急剧升高.

2)前期砂浆的温度高,预冷骨料的温度低,特征线处的温度分布极不均匀,随着水化反应不断地进行,骨料吸收热量温度升高,同时砂浆受到周围低温骨料的影响温度降低,在第15分钟左右特征线处的温度分布逐渐趋于平缓.

3)当骨料预冷处理到5、10、15℃时试件内部的最终稳定温度分别为68.89、70.38和71.87℃,与骨料不预冷的情况(最终稳定温度74.86℃)相比较,达到了降低混凝土内部温度的效果.

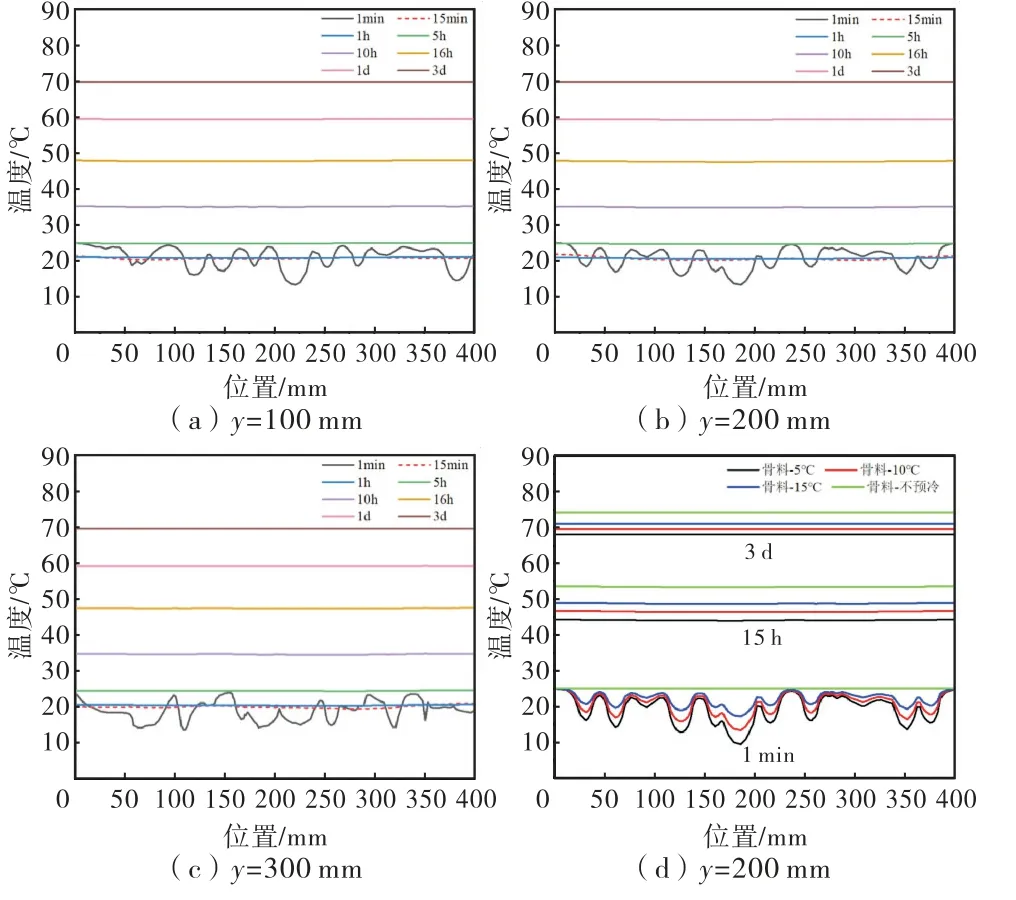
图14 特征线处的温度分布

3 结 论

基于细观尺度,运用蒙特卡罗随机投放算法,考虑泵送混凝土是由随机碎石骨料、砂浆及ITZ 组成的三相复合材料;根据室内绝热温升试验及所用材料的配合比换算出砂浆放热量并计算出其作用于整体试件的温升值,应用适用于砂浆的指数双曲线型水化度绝热温升模型,在绝热条件下研究了骨料形状、碎石骨料的投放量(胶凝材料用量)以及采取骨料预冷措施对泵送混凝土内部温度场演化过程的影响,得到如下结论和建议:

1)细观尺度温度场仿真结果与室内绝热温升试验结果吻合良好,验证了该方法在泵送混凝土内部温度场演化仿真分析中的可靠性.

2)骨料形状的差异对温度场的影响较小;骨料的体积分数对温度场的影响较大,绝热温升速率随着胶凝材料用量的增加(骨料体积分数的减小)而逐渐加快,并且最终温升值也得到了提高;在相同骨料体积分数下,温度场的时空分布会因随机碎石骨料粒径和数量的不同而发生改变,但对最大温升值和温升过程不会产生太大的影响;骨料预冷效果明显,如果夏季高温季节浇筑混凝土,有条件时可考虑骨料预冷.

3)仿真结果表明泵送混凝土的骨料粒径小、胶凝材料用大量,不利于温度控制,因此后续研究中可以考虑在保证水工混凝土可泵性的前提下对其配合比进行进一步优化;另外,要严格控制混凝土的浇筑质量,特别要关注异形结构边角处混凝土的振捣工作,保证混凝土的均匀性及密实性,减小混凝土的孔隙率,从而提高混凝土的强度及导热性能.