不确定分数阶金融超混沌系统的自适应滑模同步
孟晓玲, 毛北行, 王东晓, 陈 灿
(郑州航空工业管理学院数学学院, 郑州 450046)
混沌是非线性系统所独有的现象,具有独特的性质, 如有界性、敏感性、随机性、不可预测性等,而分数阶系统大量存在且更贴近于实际情况.同时,分数阶金融混沌系统同步问题引起了众多学者的关注[1-4],并取得了一些有价值的结果[5-7].徐瑞萍等[8]研究了三维金融系统的有限时间同步问题,在外部扰动和不确定性都是未知的情况下,通过非奇异终端滑模控制方法,设计合适的终端滑模面和控制律使混沌金融系统在有限时间内实现了同步;毛北行等[9-11]研究了分数阶具有不确定项和外扰的三维、四维金融混沌系统的滑模同步,指出在设计合理的滑模面和控制器下,金融混沌系统是可以取得同步的.本文拟在极限理论与分数阶稳定性理论的基础上,设计分数阶滑模面和控制器,并给出分数阶金融超混沌系统滑模同步的充分条件.
1 金融超混沌系统
定义1[12]连续函数x(t)的Caputo分数阶导数定义为
设计主系统为
(1)
其中x,y,z,ω分别为利率、投资需求、价格指数和经济模型的财政赤字.当a=0.9,b=0.1,c=1.5,d=0.2,k=0.17,q=0.97时, 系统(1)呈混沌态, 结果如图1所示.
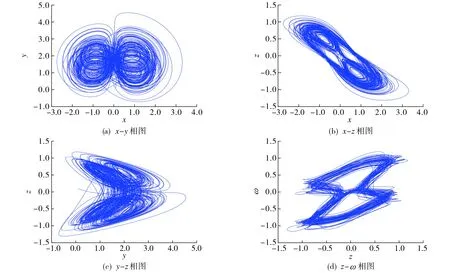
图1 系统(1)的混沌吸引子相图Fig.1 Chaotic attraction diagram of system (1)
将系统(1)看作主系统,从系统设计为
(2)
其中Δf(φ(t))为不确定项,d(t)为外部扰动, 且φ(t)=(x1,y1,z1,ω1)T.定义主从系统的误差分量为e1=x1-x,e2=y1-y,e3=z1-z,e4=ω1-ω,则有
(3)
引理1[13]若x(t)为连续可微的函数, 则有
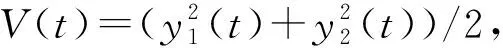
假设1|Δf(φ(t))|≤m, |d(t)|≤n, 且m,n为正的未知常数.
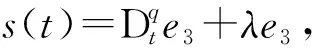
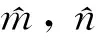
2 三维金融混沌系统
上述方法对三维金融混沌系统同样适用.设主系统为
(4)
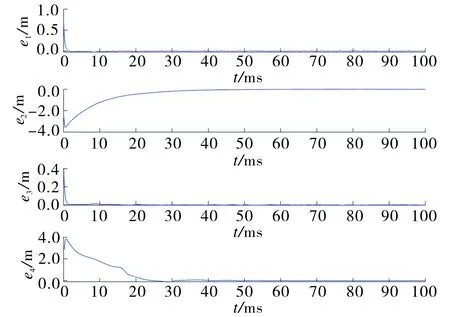
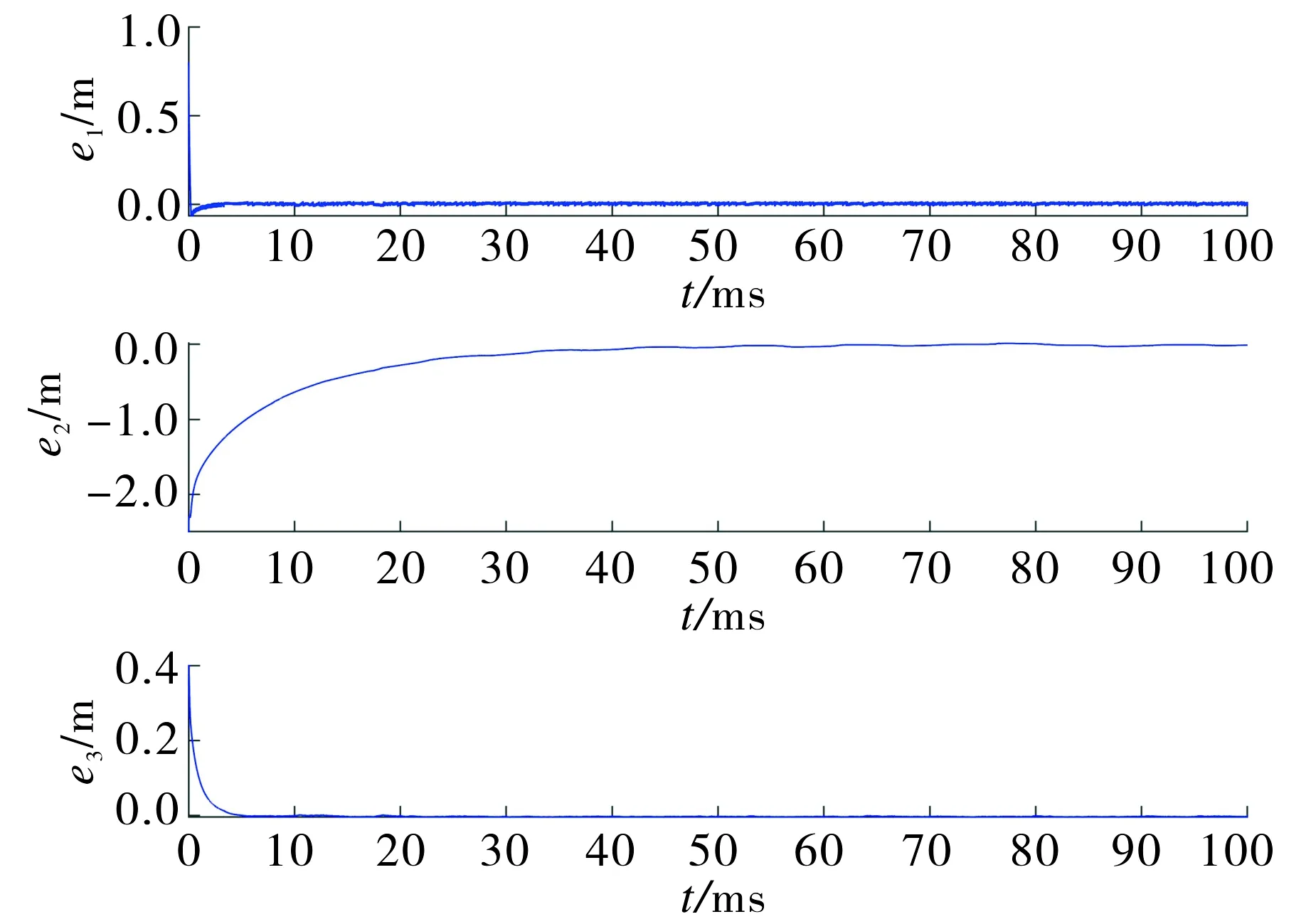
其中0 (5) 其中Δf(φ(t))为不确定项,d(t)为外部扰动, 且φ(t)=(x1,y1,z1)T.定义主从系统的误差分量为e1=x1-x,e2=y1-y,e3=z1-z则有 (6) 设四维金融系统参数为a=0.9,b=0.1,c=1.5,d=0.2,k=0.17,q=0.97,初始值(x(0),y(0),z(0),ω(0))=(2.2,6.5,2.5,1.5), (x1(0),y1(0),z1(0),ω1(0))=(3,4,3,4.5), 三维金融系统参数为a=0.9,b=0.1,c=1.2,q=0.93, 初始值(x(0),y(0),z(0))=(2.2,6.5,2.5), (x1(0),y1(0),z1(0))=(3,4,3), 不确定项和外部扰动为Δf(φ(t))+d(t)=0.1sin(tx1)+0.1cos(t). 图2~3是两个定理的误差曲线.结果显示, 两者初始时误差均较大, 但随着时间的推移, 系统误差越来越小, 并最终趋近于0, 说明2个系统均取得了混沌同步. 图2 定理1中的误差系统曲线Fig.2 The system error curves of theorem 1 图3 定理2中的误差系统曲线Fig.3 The system error curves of theorem 2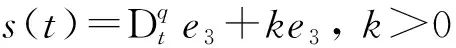
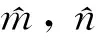
3 数值仿真