基于G1-变异系数-KL改进TOPSIS雷达对抗干扰有效性评估

李志军，向建军，盛涛，肖冰松

（空军工程大学航空工程学院，西安 710038）

在现代空战中，雷达对抗的重要性越来越凸显出来，雷达干扰有效性评估是电子攻击观察-调整-决策-执行（Observe-Orient-Decide-Act，OODA）环的重要组成部分，准确对雷达对抗中干扰效果进行评估，不仅关乎作战行动的成败，而且对电子战战术的提升也有重要的作用。

针对雷达对抗干扰有效性评估的问题，国内外的主要研究成果有：崔炳福［1］系统介绍了雷达对抗干扰有效性评估理论。王博阳［2］针对传统评估方法未全面考虑作战对象不确定性、评估结果的时效性的问题，提出了一种在线评估的方法，但是该方法未能充分考虑专家经验对干扰有效性评估的影响。董家隆等［3］针对天波雷达的作战适应特点在传统模数转换（Analog to Digital Converter，ADC）基础上增加了电磁环境影响因子，评价结果更加科学，但是无法体现系统中各个因素对效能的影响，并且在实际情况中评估复杂的雷达对抗系统时较难实现。徐沙和张洁［4］提出了一种改进层次分析法（Analytic Hierarchy Process，AHP），通过专家评估的方法获得重要性指标，按照雷达干扰逐层计算评估结果。石亮［5］和史彦斌等［6］分别提出了将AHP法与云理论结合的航空电子对抗有效性评估，该方法先通过AHP法确定指标的权数，再通过云运算方法获得评估结果，但是这类方法都过于依赖专家的经验，客观性不足，主观性偏重，无法对实际作战应用产生积极影响。李婧娇［7］用基于模糊数学中Vague集的模糊决策方法进行了机载电子对抗系统的干扰有效性评估，通过模糊数学较好地解决了模糊因素的影响，但是在确定指标的权数时仍然过于依赖专家的主观经验。

Qi和Wang［8］将灰色关联分析引入干扰有效性评估模型，基于灰色理论能够较好地解决不确定因素的影响，但是基于灰色系统评估方法还不够成熟，学术界对该方法的理解不一致，至今仍缺少系统性的理论支撑。

现有的雷达对抗干扰有效性评估体系多采用信息准则、战术应用准则、信息损失等准则在内场实验的条件下选取评价指标，并没有考虑在实际的雷达对抗场景中，干扰方与雷达是非合作方，此时传统的评价指标并不都能通过侦察设备实时获取［9］。

逼近理想解排序法（Technology for Order Preference by Similarity to an Ideal Solution，TOPSIS）是解决多属性决策问题的一种高效算法，能够综合考虑影响决策与评估的多个不同的属性。TOPSIS算法在电能质量［10］、空战威胁［11］和环境风险［12］中的应用都有较好的效果。但是传统TOPSIS算法仍然存在问题：一方面传统TOPSIS算法在确定属性权值时过于主观；另一方面在使用欧氏距离评价效果时，对于位于正理想解与负理想解中垂线上的属性无法进行有效性评估［13-15］。当相对熵用于概率分布差别的非线性度量时，可以有效解决该类问题。

基于上述问题，本文提出一种基于G1-变异系数-KL的改进TOPSIS算法进行雷达对抗干扰有效性的评估。G1法能够充分反映评估者的意志，而变异系数法综合利用指标中的所有信息，能够克服指标过于主观的问题，并且引入差异系数能够充分反映主客观程度；相对熵又称为KL散度，不对称并且不满足三角不等式［16］，对于正负理想解中垂线上的点仍能进行有效分析。本文算法改善了传统TOPSIS算法的局限性，扩展了TOPSIS算法的应用范围，提高了干扰效能评估的可信度，并且对作战中雷达电子对抗的战术使用具有相当的参考价值。

1 雷达对抗干扰有效性评估模型

雷达干扰是一个双向的过程。干扰平台产生干扰，对雷达平台进行干扰，因此衡量干扰效能时应该同时考虑雷达方和干扰方的因素，即分析雷达受到干扰采取抗干扰措施，指标前后发生的变化评价干扰效果。雷达抗干扰措施可以从能量域、频域、空域和时域进行分类，由于干扰方与被干扰方是密切相关的，在分析干扰性能时就可以把雷达抗干扰措施作为分析对象，分析抗干扰措施所对应的指标的变化，来综合评价干扰有效性。

在雷达对抗领域，每个作用域的抗干扰措施都对应着诸多评价指标，但是只有很少的指标能够实时获取，因此在选取指标时，基于合理性、系统性和科学性的原则，考虑在实际雷达受到压制时干扰场景中雷达侦察能实时获取的指标，征询电子战领域专家的意见后，构建了如图1所示的对象-指标的2层干扰效能评估体系。

图1 雷达对抗干扰有效性评估2层指标Fig.1 Two levels indicator of radar anti-jamming effectiveness evaluation

1.1 时域干扰效果指标

1）脉冲宽度。雷达工作的占空比定义为

式中：τ为脉冲宽度；T为脉冲重复周期。占空比与平均发射功率成正比，雷达可以通过保持脉冲重复周期不变的情况增加占空比即增加脉冲宽度来提高发射功率［17］，即脉冲宽度越宽，干扰效果越好。

2）脉冲压缩比。脉冲压缩比的值就是在信号能量不变的前提下雷达发射功率提高的倍数，当雷达受到干扰后会提高脉冲压缩比以提高探测性能。

脉冲压缩技术能够有效提高雷达发射机的平均发射功率。脉冲压缩比越高，干扰效果越好。

3）脉冲重复频率。脉冲重复频率与脉冲重复周期互为倒数，雷达的最大探测距离可以表示为

式中：c为光速。受到干扰的雷达为了保证其最大探测距离会增加脉冲重复周期，即脉冲重复频率越小，干扰效果越好。

1.2 空域干扰效果指标

1）波束偏移角度。波束偏移角度是指雷达天线主波束偏离目标的角度。波束指向的变化极易侦察。波束偏移的角度越大，说明干扰效果越好。

2）波束驻留时间。波束驻留时间是雷达信号指向真实目标的总时间。对于多普勒分辨率ΔV：

式中：λ为雷达工作波长；t为波束驻留时间。雷达受到干扰，多普勒分辨率下降，雷达天线就会降低波束驻留时间以提高多普勒分辨率，即波束驻留时间越短，干扰效果越好。

1.3 频域干扰效果指标

雷达的距离分辨力与带宽成反比，距离分辨力越小，工作性能越好，当雷达受到干扰，其距离分辨性能变差，为提高距离分辨性能，雷达会采用宽带信号。因此干扰效果越好，雷达的带宽越宽。

1.4 能量域干扰效果指标

雷达峰值功率是指脉冲发射期间射频振荡的平均功率。雷达受到干扰后，会提高峰值功率来维持工作性能，因此干扰效果越好，雷达峰值功率越高。

2 基于G1-变异系数法的组合赋权

确定评估指标的权重通常使用主观赋权法、客观赋权法和组合赋权法。传统的干扰有效性评估方法中，通常使用专家赋权法［9］，但是这种方法过于主观，不能充分利用已有信息，并且会造成较大的误差，使用组合赋权法能够减少单一赋权造成的信息损失，因此利用组合赋权法确定要评估的指标的权重。为了使主观赋权与客观赋权的一致性更强，引入差异系数的概念，使结果更加充分地体现主观性和客观性。

2.1 G1法确定指标主观权重

G1法［17］的主观性较强，能够很好地反映出专家的想法或者评估者的经验。G1法是先对评价指标进行排序，再比较判断相邻指标的重要性的一种方法，其步骤如下：

2.2 变异系数法确定指标客观权重

变异系数是标准差与平均值的比值，也称标准差率，能够用来衡量随机变量的不确定性，变异系数在衡量不确定性时，不依赖任何先验知识，能够客观反映某个数据与总体之间的关系。该方法的基本思想是：根据某项有效性评估指标对所有指标的变异程度确定权值，若某项指标变异程度较大，说明评价对象达到该指标的平均水平难度较大，该指标就可以有效区分所有评价对象在这个方面的能力，应该赋予较大的权值。反之，应该赋予较小的权值。采用标准差系数可以在统计学意义中有效消除平均数大小的影响。评价步骤如下：

步骤3 归一化变异系数，计算各个指标的权数：

根据式（14）就可得到由变异系数法确定的权变量矩阵WBY＝［ω′1ω′2… ω′n］T。

2.3 基于离差最小化的组合赋权

为了充分利用已有的信息，使用组合赋权的方法可以得到最终的权重向量：

将式（20）、式（21）代入式（16），就可以得到组合权重。

3 G1-变异系数-KL改进TOPSIS干扰有效性评估

该算法的核心思想是：先计算得到正理想解和负理想解，搜寻离正理想解尽量近并且离负理想解尽量远的值，计算出相对贴近度，比较所有相对贴近度后给出评价结果。改进TOPSIS算法的工作流程如图2所示。

图2 G1-变异系数-KL改进TOPSIS算法流程Fig.2 Flowchart of G1-variation-coefficient-KL TOPSIS algorithm

G1-变异系数-KL改进TOPSIS算法具体应用步骤如下：

步骤1 构建干扰有效性评估的数据评价矩阵：

A矩阵表示有m个评价对象，这些对象的n个指标进行评价，xij表示第i（i＝1，2，…，m）个对象的第j（j＝1，2，…，n）个评价指标所对应的原始值。

步骤2 对A的每一列进行归一化处理。消除不同指标之间的量纲和数量级的影响，便于在同一尺度上进行评判，将属性划分为效益性指标和成本性指标，分别进行规范化。规范化后的效益性指标为

式中：J+＝｛j＝1，2，…，n｝并且第j个属性属于效益型指标，即指标值越大所得效益越高；J-＝｛j＝1，2，…，n｝并且第j个属性属于成本型指标，即指标值越大所得绩效越低。

步骤7 干扰有效性评估。对得到的相对贴近进行降序排列，显然相对贴近度越大，代表干扰的效果越好。

4 仿真分析

现得到在某次雷达对抗仿真中在压制性干扰条件下由我方雷达得到的脉冲重复频率、带宽、脉冲压缩比、脉冲宽度、波束偏移角度、峰值功率和波束驻留时间，如表1所示。仿真实验利用本文提出的算法、传统TOPSIS算法和极大熵TOPSIS算法对该电子战场景下的干扰效能评估，通过比较结果验证算法的性能。

表1 雷达反馈数据Table 1 Radar feedback data

通过征询专家的意见以及参考过往的效能评估经验，可以得到在压制性干扰条件下上述指标的重要性从大到小排序为：波束驻留时间＞波束偏移角度＞峰值功率＞脉冲重复频率＞脉冲压缩比＞带宽＞脉冲宽度。

将上述属性分别记为a1、a2、a3、a4、a5、a6、a7，通过1.1节中雷达参数属性的分析可知，a1、a4为成本性指标，a2、a3、a5、a6、a7为效益性指标。根据指标性质以及式（23）、式（24）的归一化处理过程，得到归一化评估矩阵，如表2所示。

表2 归一化评估矩阵Table 2 Normalized evaluation matrix

按照2.1节介绍的利用G1法确定主观权重的方法，根据专家实际工作经验，进行判断给出r2＝1.2，r3＝1.3，r4＝1.4，r5＝1.6，r6＝1.6，r7＝1.1，将上述数据代入式（8）和式（9）可以得到利用G1法确定的主观权重矩阵WG1为

将得到的组合权值代入第3节中介绍的改进TOPSIS算法，可以得到利用G1-变异系数-KL的TOPSIS得到有效性评估贴近度，如表3所示。

表3 G1-变异系数-KL改进TOPSIS算法有效性评估贴近度Table 3 Effectiveness evaluation closeness using G1-variation-coefficient-KL TOPSIS

为验证本文提出的算法性能，将文献［18］提出的极大熵-TOPSIS算法和传统TOPSIS算法作对比。利用文献［18］中的极大熵算法确定的权值为

用极大熵法确定权重后，利用传统TOPSIS算法得到的有效性贴近度如表4所示。

表4 极大熵法权重有效性贴近度Table 4 Effectiveness evaluation closeness using maximum entropy to calculate weight

利用传统TOPSIS算法得到的有效性贴近度如表5所示。

表5 传统TOPSIS算法的有效性贴近度Table 5 Effectiveness evaluation closeness traditional TOPSIS algorithm

对相对贴近度进行排序，可以得到3种算法对干扰有效性的评估结果，如表6所示。

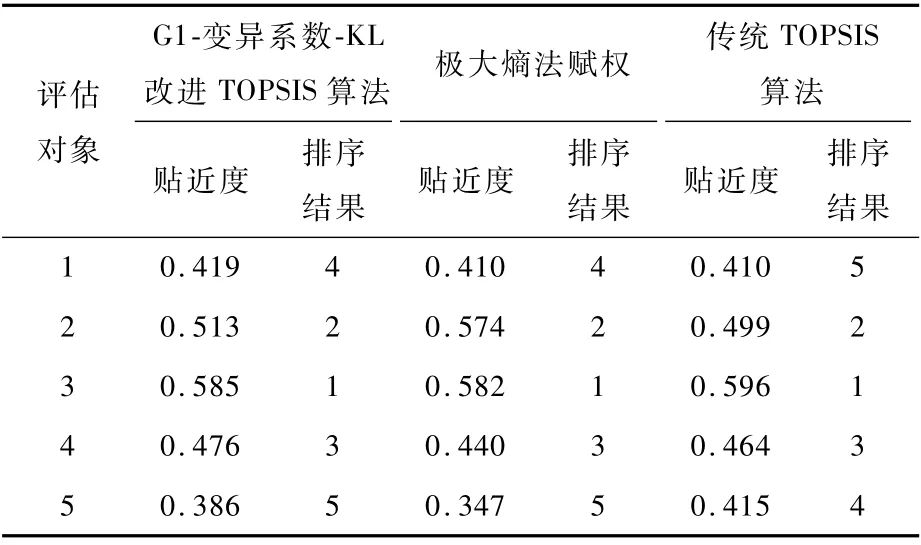
表6 雷达对抗干扰有效性评估结果Table 6 Anti-jamming effectiveness evaluation results

为了更加直观地比较雷达对抗干扰有效性的结果，绘制图3。如图3所示，3种算法在排序上对第1、5组数据出现了一定的分歧，但是从原始数据和实际在外场测试的工作效果来看，第1组施加干扰时效果明显要好于第5组。由此可见，改进的算法能够充分体现决策中各种主客观因素的影响，极大程度上避免排序的错误，从而有效提高电子对抗评估的有效性。另外，改进的算法得到的贴近度的方差和极差分别为0.006和0.2，传统TOPSIS算法求得的贴近度的方差和极值分别为0.005和0.18。显然本文提出的改进TOPSIS算法得到的评估结果区分度更大，更容易排序。

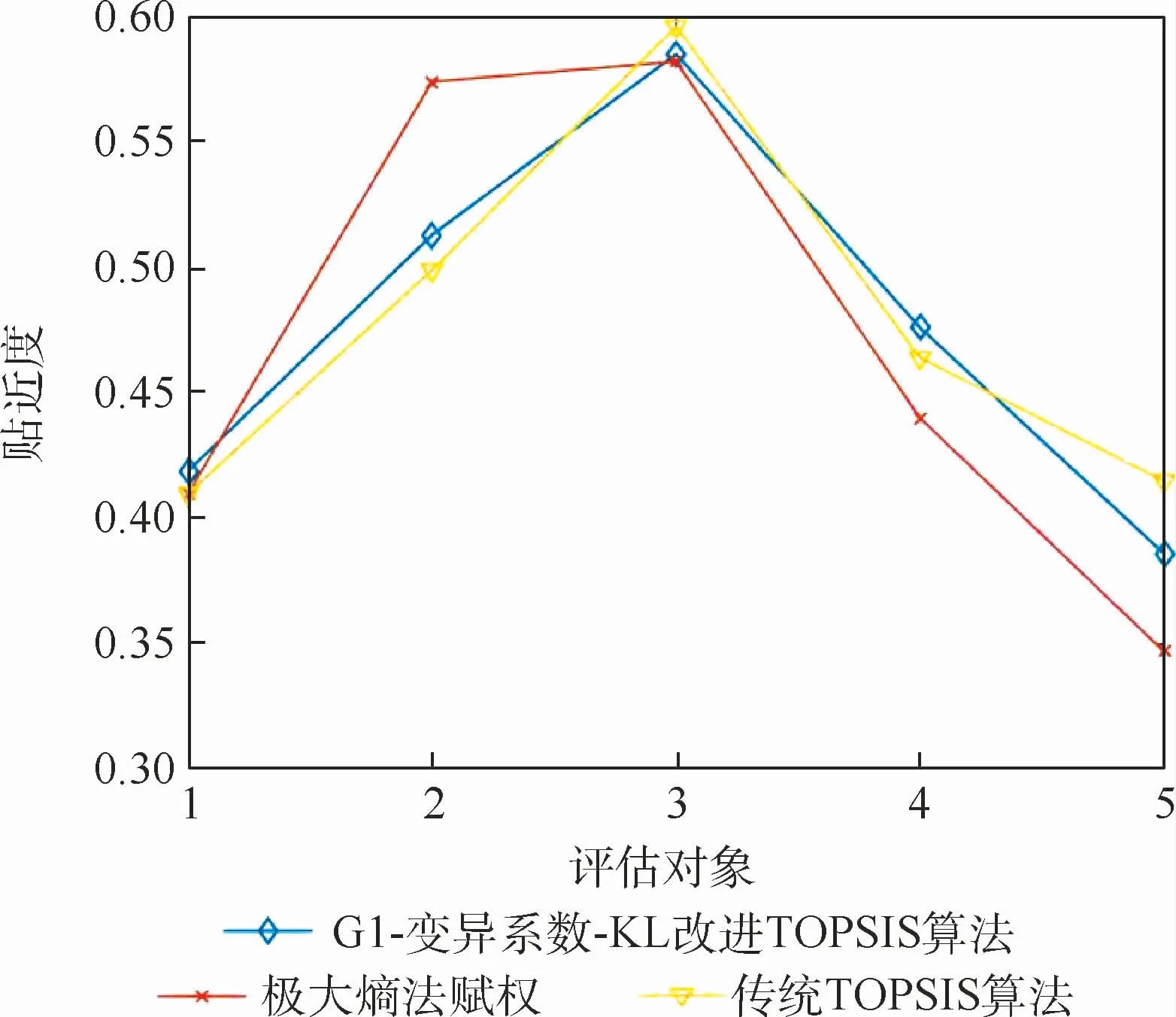
图3 不同算法的雷达对抗有效性评估结果Fig.3 Radar anti-jamming effectiveness evaluation results of different algorithms

5 结 论

针对传统TOPSIS算法，在进行多属性决策时不能充分结合主客观因素，并且在特定情况下存在评估模糊的问题，利用变异系数、G1和相对熵对传统TOPSIS算法进行改进，构建了电子对抗效能有效性的评估模型。

1）在进行雷达对抗有效性评估时，无法得到被干扰方的全部信息，在建立有效性评估体系的基础上，运用变异系数法得到的主观权重和G1法得到的客观权重进行组合得到组合权重，避免了单独赋权带来的信息损失，充分反映影响评价的各个因素。

2）针对传统算法评价的指标值位于正负理想解中垂线上会造成评估模糊的问题，将相对熵与传统TOPSIS算法结合，解决了评价模糊的问题。

3）通过与传统的算法进行仿真对比，改进的算法不仅能够有效得对雷达干扰的效果进行评价，还具有较高的分辨率，提高了评估的准确性。

4）改进的评价算法是属于决策领域的传统问题，对产品效能评价、作战决策其他评价类或者决策类问题具有一定程度的借鉴意义。