转盘轴承集聚效应分析及其对回转性能的影响

邓飙，陈渐伟，郭杨，唐圣金，陈威

（火箭军工程大学，西安 710025）

转盘轴承是用于航天发射台的关键部件，具有尺寸大、载荷重等特点，一般使用离散的隔离块，以保持滚动体平稳运动。航天发射台使用的转盘轴承在连续回转工作中发现台体发生变形，部分滚动体间隙增大，伴随出现隔离块滑落及滚动体集聚的现象，这种现象为转盘轴承集聚效应。

对于滚动轴承间隙和刚性的研究一直备受关注，多数研究对象一般是针对高速转动的小型滚动轴承，在建模分析时通常会忽略轴承实际装配条件，通常考虑在一个或多个具有固定自由度的载荷作用下轴承间隙或滚道刚性的变化特征［1-2］，忽视了大型滚动轴承在动态载荷条件下，滚道刚性和滚动体接触作用力的时变性与转盘轴承间隙变化的联系，以及间隙变化对于大型滚动轴承回转性能的影响。Jones等［3-5］的滚道控制论是轴承运动学问题的研究基础，Harris和Kotzalas［6-7］在此基础上第一次详实全面地建立了基于滚动体与滚道变形协调关系的拟静力学方程，这一研究成果是现代分析轴承刚度特征的重要基础之一。实践表明，滚道控制论具有一定的局限性［8-9］，张进华等［10］通过改变轴承初始位置的状态，提出了普适性更强的轴承建模方法和理论，在此基础上分析了不同载荷条件下轴承刚性的变化规律。邵毅敏和涂文兵［11］考虑了轴承座和套圈变形对轴承运动特性的影响，发现随着载荷增大轴承径向刚度呈非线性变化，径向游隙越大，轴承各部件振动动能越大。对于大多数系统，轴承的刚度具有时变性［12-14］。刘光辉等［15］通过改进传统算法，对圆柱滚子轴承刚度的非线性时变特征进行了定量分析，并以有限元方法验证了改进算法的准确性。姚廷强等［16］在柔性多体力学的基础上，综合考虑了接触刚度等非线性时变因素，对滚动轴承的时变振动特性进行分析。运侠伦等［17］提出了一种实时测试动态支承刚度的方法，采取仿真实验相结合的方式，验证了测试方法的可靠性。

目前关于轴承间隙的研究，多以保持架兜孔与滚动体之间的间隙为主要研究内容。Ghaisas等［18］结合保持架在空间中的运动状态，建立了关于保持架六自由度运动方程，以分析兜孔间隙等多种因素对其运动稳定性的影响。姚廷强等［19］通过ADAMS软件建立了保持架的动力学模型，分析了多种工况条件下保持架间隙和润滑状态的变化对其运动平稳性的影响。邓四二等［20］以角接触球轴承为研究对象，建立了关于其保持架的柔性动力学运动模型，结果表明，角接触球轴承引导间隙与兜孔间隙之比影响保持架转动的平稳性。大量的研究显示由于兜孔与滚动体之间存在间隙［21-22］，滚动体在兜孔内是一个不断的碰撞过程，造成保持架运动不平稳。

转盘轴承通常采用隔离块使滚动体均匀分布在滚道，滚动体与隔离块存在装配间隙。为探究集聚效应与这种转盘轴承间隙的因果关系，以及对转盘轴承回转性能的影响，以航天发射台使用的转盘轴承为研究对象，对比了不同滚道结构下，转盘轴承各滚动体接触力和滚道变形的变化规律，在此基础上分析了转盘轴承间隙的变化，对集聚效应的原因做出了解释且提供了解决方案。以航天发射台为主体，搭建转盘轴承的回转实验平台，进一步验证了集聚效应对摩擦力矩的影响，证明了分析结果的正确性，同时也验证了优化方案的有效性。

1 数值方法的实验验证

1.1 实验系统

航天发射台转盘轴承回转性能实验平台主要由加载设备、传动系统、发射台和液压系统台构成，如图1所示。液压系统驱动加载设备向发射台施加轴向载荷，并通过传动系统驱动发射台回转，可以模拟发射台实际负载条件。

图1中的加载设备由上十字架、液压缸、回转轴承和十字底座构成，如图2所示，加载设备上十字架与支撑臂通过螺栓固定连接，液压缸拉动十字架对支撑臂施加轴向载荷。当发射台回转时，支撑臂带动十字架使加载设备回转部同步回转，可对发射台产生一个可回转的轴向负荷。

图1 转盘轴承回转实验平台Fig.1 Turntable bearing rotary experimental platform

1.2 发射台工位分析

航天发射台初始工位支撑臂位于支撑腿正上方的位置，支承臂与支承腿之间夹角为0°，通常称作0°工位。在回转90°后，支承臂回转至下一支撑腿的正上方时，发射台再次回归至0°工位，因此，发射台每回转90°为一个回转周期。发射台结构具有严格的对称性，当发射台从0°工位逆时针回转至45°工位，与从90°工位（即下一个0°工位）顺时针回转至45°工位，发射台实际承载变化是对称的，且45°工位为分界点。

1.3 发射台有限元模型建立

发射台回转速度缓慢，其运动过程是准静态过程，选取典型工位下的发射台，建立相应的有限元静力学模型，采用隐式求解器进行计算。

在计算过程中对模型进行了相应简化，忽略了发射台中铰孔、螺栓等零部件的细节结构以便于结构化网格划分。

在图2中，垂直的支承臂与上框架的支座通过销轴连接，轴向载荷通过支座的轴孔传递至发射台，在有限元分析时为避免集中力直接作用在节点上引起有限元模型不收敛，在每个支座轴孔中心处建立参考点，将参考点与轴孔内表面建立耦合的约束关系，通过节点施加轴向载荷，间接作用在支座上。发射台4个支撑腿与地基固定连接，对4个支撑腿的底面施加固定约束；回转部可相对固定部回转运动，对上框架内侧圆周面施加轴向回转约束。有限元模型的边界条件和载荷施加方式如图3所示。

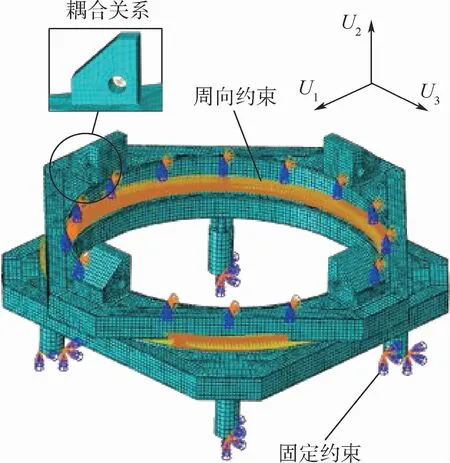
图3 航天发射台有限元模型Fig.3 Finite element model of space launch pad

1.4 接触关系设置

发射台转盘轴承滚动体数量多达298个，若一一建立滚动体与滚道之间的接触关系，则有限元模型难以收敛。模型采用Connector轴向连接器模拟滚动体和滚道的接触关系，如图4所示。

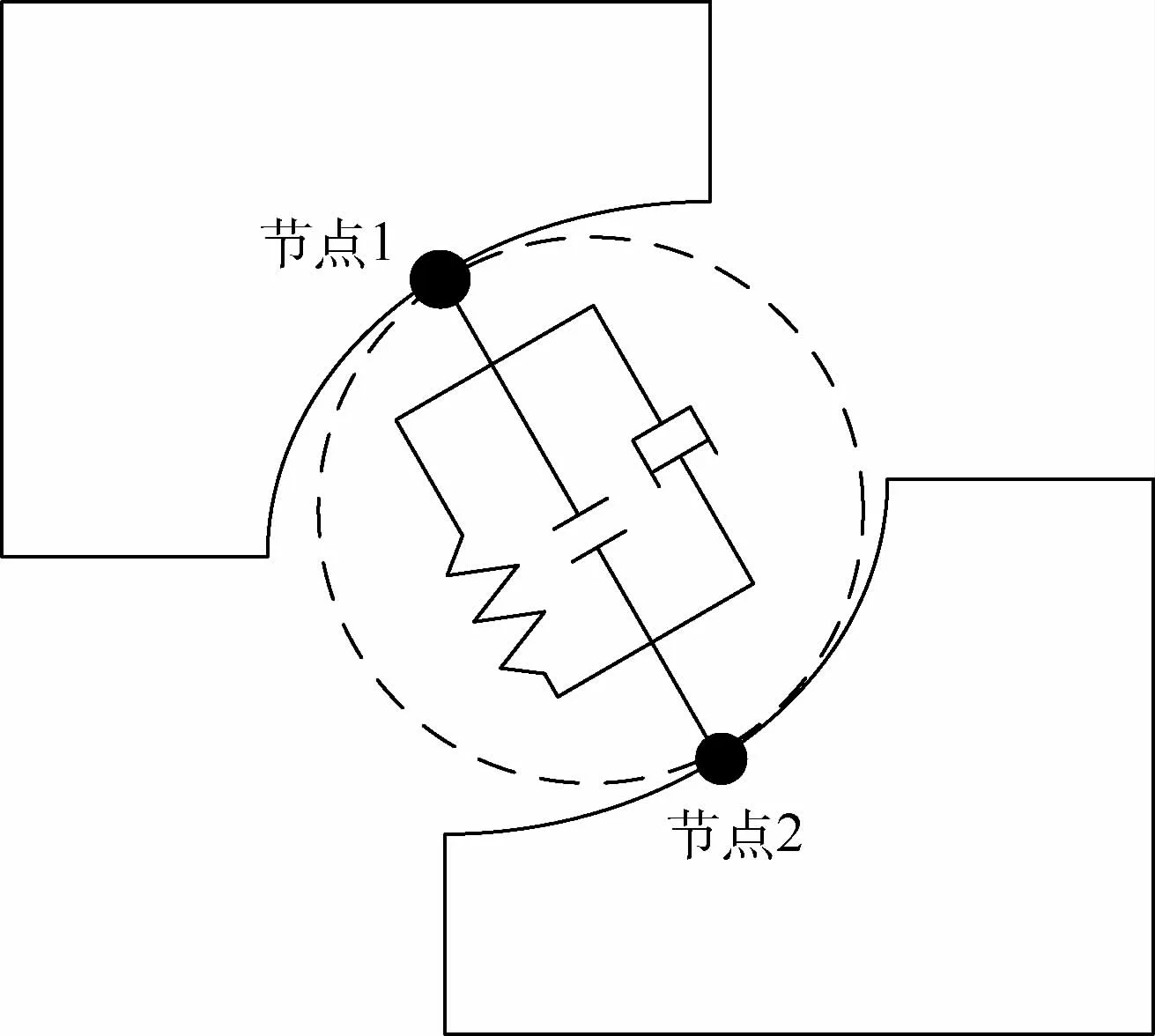
图4 轴向连接器Fig.4 Axial connector

1.5 数值分析及实验验证

依次选取航天发射台逆时针回转过程中0°、15°、30°和45°四个工位，进行有限元分析，并通过静载实验测量发射台下框架最大变形位，以验证有限元计算的准确性。

4个工位的发射台下框架轴向位移变化云图如图5所示，最大轴向变形位置为下框架中央断面的位置。

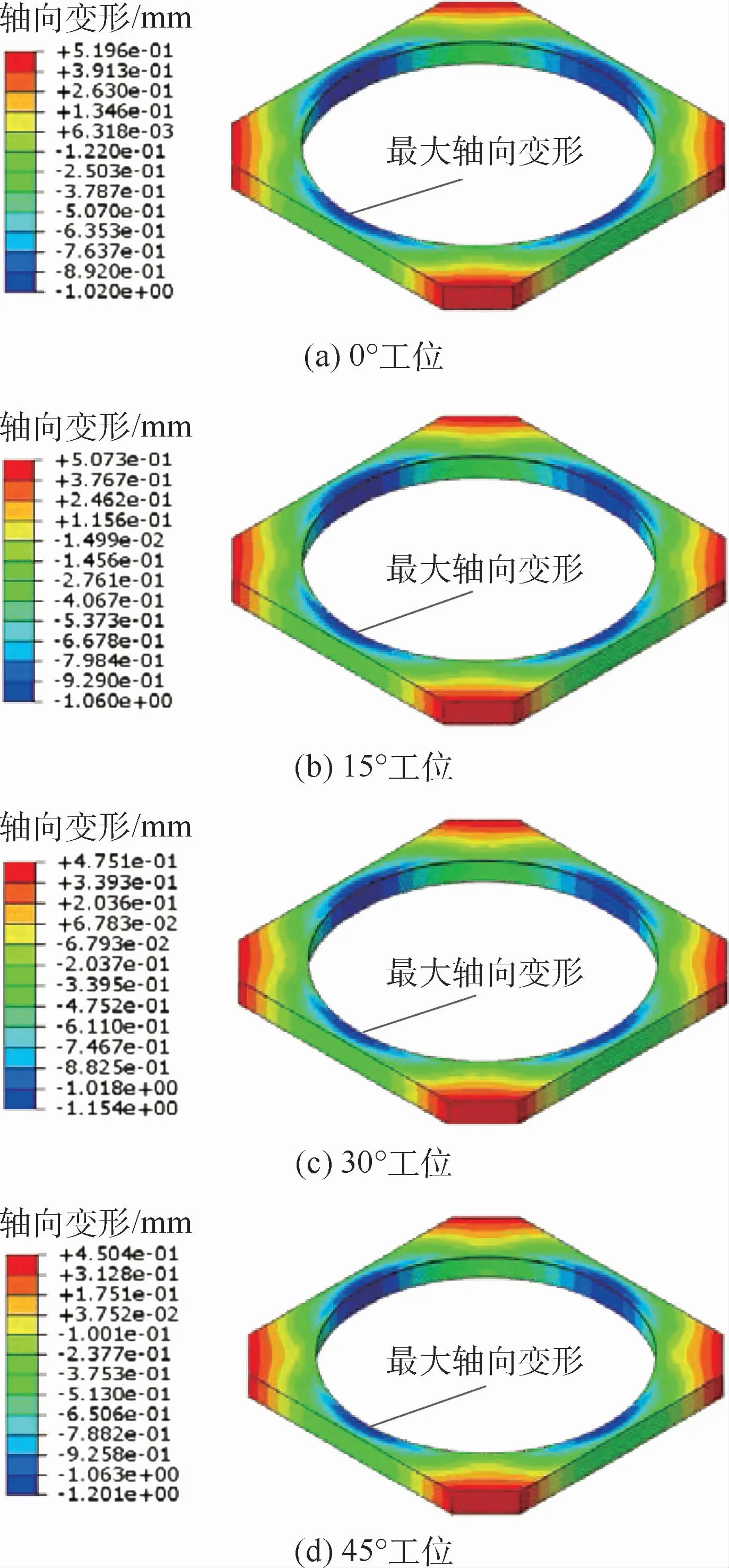
图5 航天发射台下框架轴向位移云图Fig.5 Axial displacement contour of lower frame of space launch pad

为检验有限元模型准确性，在静载实验中将千分表固定在与地基相连的钢板上，如图6所示，对中央断面的位置进行多次测量，取均值为实验结果。

图6 下框架变形测量图Fig.6 Deformation measurement of lower frame

4个工位中，下框架轴向变形的有限元计算结果和测试结果对比如图7所示。各个工位下的误差范围在9.5%以内，满足工程计算的需求，因此，建立的有限元模型是可靠的。

图7 下框架轴向变形的验证Fig.7 Verification of lower frame axial deformation

2 滚动体集聚效应的原因分析

2.1 滚动体定义

为便于后文描述滚动体相关参数，采用相位角对不同位置上的滚动体进行定义。发射台上的滚动体分布如图8所示，以支撑腿1正上方中心位置为起始位置，记该位置上滚动体的相位角为0°，并以此位置为起点，沿发射台逆时针方向，滚动体的相位角逐渐增大，第i个滚动体的相位角φi可表达为

图8 滚动体相位角分布图Fig.8 Phase angle distribution of rolling body

式中：n为滚动体数目；φi表示第i个滚动体的相位角。

2.2 滚动体驱动力的分布特征变化

滚道对滚动体的摩擦力是滚动体回转驱动力，通常认为滚动体与滚道之间的摩擦力符合库伦摩擦力定律，即在摩擦系数不变的情况下，滚动体与滚道的接触作用力与驱动摩擦力呈正比关系，因此，研究各个滚动体接触压力可以分析滚动体的运动状态。在有限元后处理模块中通过对Connector连接器的轴向力进行历程输出，即可得到滚道中各个滚动体的接触作用力。

2.2.1 单排2点接触式转盘轴承接触作用力分布

单排2点接触式转盘轴承中，滚动体接触作用力的分布规律如图9所示，呈近似三角波周期性变化。在0°工位时，承载臂位于滚道正上方。随着发射台转动，4组工位中出现最大接触压力的位置逐步增大，相位角依次是0°、15°、30°和45°。回转过程中各个滚动体接触作用力分布规律具有时变性，沿相位角增大方向移动，波峰始终位于载荷施加的正下方。

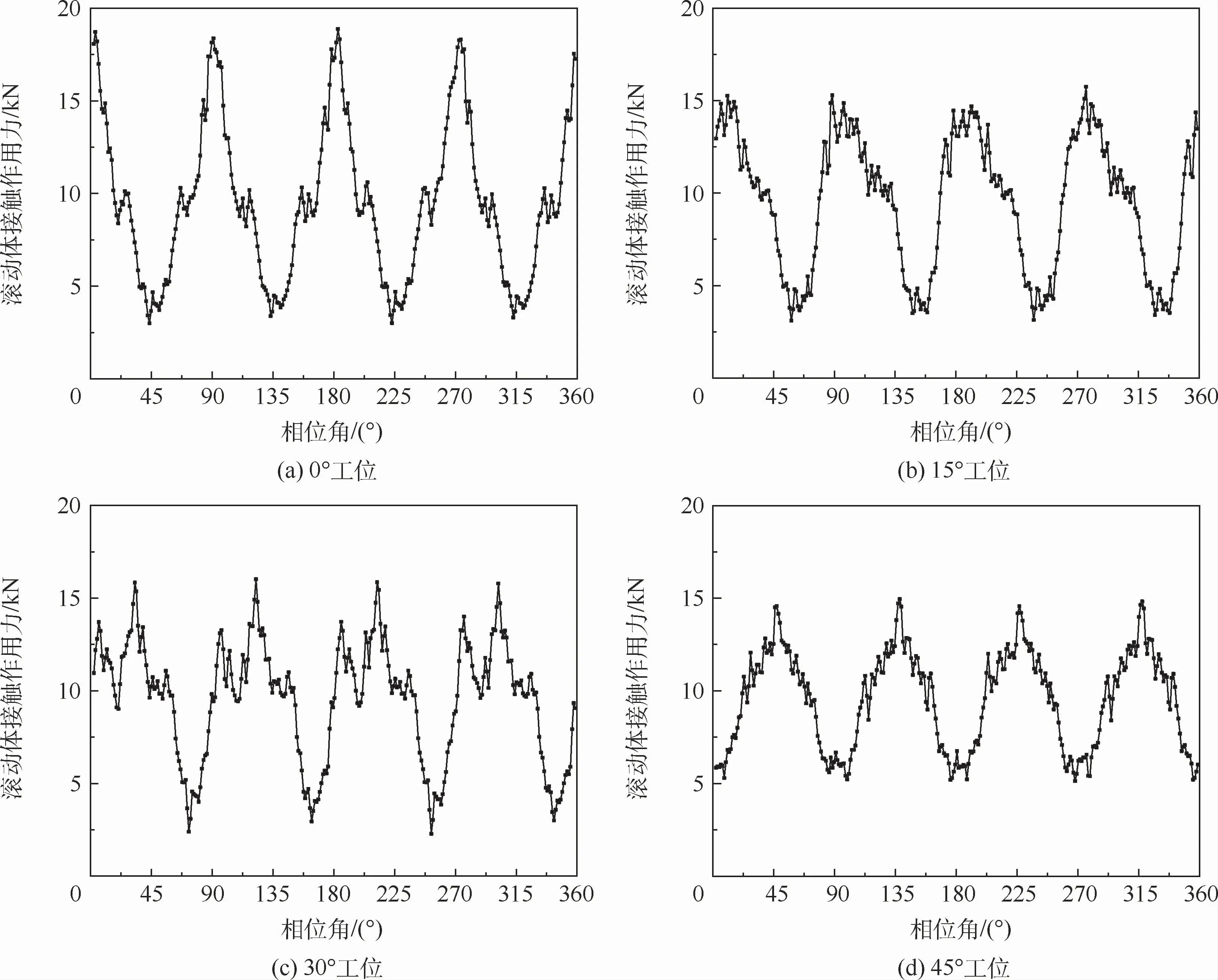
图9 单排2点接触式转盘轴承滚动体接触作用力Fig.9 Contact force of rolling body of single-row two-point contact turntable bearing

2.2.2 单排4点接触式转盘轴承接触作用力分布

为便于描述单排4点接触式转盘轴承中接触作用力分布规律，对连接单元进行分组，如图10所示，转盘轴承中上滚道外侧接触面与下滚道内侧接触面的连接单元记作A；上滚道内侧接触面与下滚道外侧接触面的连接单元记作B。

图10 4点接触式转盘轴承连接单元定义Fig.10 Definition of connection unit of four-point contact turntable bearing

各滚动体接触作用力变化如图11所示，发射台在0°工位时，各相位角中的滚动体两侧接触作用力分布规律相同。在15°工位时，滚动体两侧接触作用力的分布曲线出现相位差，单个滚动体两侧的接触作用力开始发生变化，随着发射台继续回转，单个滚动体两侧的接触作用力的差异逐步增大，滚动体两侧接触作用力的变化曲线相位角相差90°。

图11 单排4点接触式转盘轴承滚动体接触作用力Fig.11 Contact force of rolling body of single-row four-point contact turntable bearing

相比于单排2点接触式转盘轴承，单排4点接触式转盘轴承的滚动体两侧始终受力，与滚道为4点接触关系，滚动体在滚道内具有较好的稳定性。但滚动体的接触作用力在发射台回转过程中同样不断变化，导致各个滚动体回转速度不断改变。

2.3 滚道刚性变化对转盘轴承间隙的影响

2.3.1 滚动体位移计算方法

Connector轴向连接单元与滚道存在2个连接节点，为模拟滚动体球心的位移，在ABAQUS后处理模块中，对各个滚道的连接节点分别建立PATH进行路径输出，并对同一连接单元两端节点的各个方向的位移做均值处理，以表示对应滚动体球心的位移变化，如图12所示。

图12 连接单元各节点位移关系Fig.12 Displacement relation of nodes of connection unit

2.3.2 滚道轴向位移的影响

滚动体始终沿下滚道接触面滚动，研究下滚道的轴向变形有助于分析滚动体的运动轨迹。

在任意工位下，滚动体轴向位移的分布规律呈近似的三角函数变化，如图13所示。以相位角0°～90°的区间为例，2组转盘轴承的下滚道轴向变形趋势均为先增加后减少，在相位角为45°的位置时达到最大。因此，滚动体在回转过程中不断经历“爬坡”和“下坡”的过程。

图13 转盘轴承下滚道轴向位移变化Fig.13 Changes of axial displacement of lower raceway of turntable bearing

2.3.3 滚道径向位移的影响

单排2点接触式转盘轴承的径向位移变化曲线如图14所示。上滚道和下滚道的径向位移变化曲线的波形近似为三角函数。随着航天发射台回转，滚道位移的波形沿回转方向发生移动，但滚动体径向位移的波形相位不发生变化。因此，工位的变化对于滚动体径向位移的分布规律并无影响，4个工位下，滚动体径向位移呈余弦函数的规律分布，发射台的回转过程仅对滚动体径向位移变化曲线的波峰和波谷的大小产生影响，可较好地用于衡量转盘轴承径向刚度。

单排4点接触式转盘轴承的径向位移如图15所示，上滚道、下滚道和滚动体的径向位移具有相同的波形，且呈周期性变化。

相对于2点接触式转盘轴承，4点接触式转盘轴承滚动体平均径向位移依次下降了156.47%、323.6%、283.0%和93.4%，如图16所示，因此，4点接触式转盘轴承径向刚度较好。

图16 滚动体径向位移对比Fig.16 Comparison of radial displacement of rolling body

2.3.4 径向刚度变化对滚动体间隙的影响

当滚动体发生径向位移时，转盘轴承间隙发生变化，由图14和图15可知，各个相位角上的滚动体沿径向发生不同程度的位移，无法直接计算间隙增加的大小，结合滚动体的径向位移变化曲线，采取如下计算方法。

将图14和图15的数据代入式（7）可得各个工位下不同转盘轴承的间隙变化，如图18所示。随着航天发射台回转，转盘轴承内间隙增加数值是不断变化的，当发射台从0°工位回转至45°工位时，轴承间隙增加值变化为先增加后减少。单排4点接触式转盘轴承由于具有较好的径向刚度，间隙增加值远小于2点接触式转盘轴承。

图14 单排2点接触式转盘轴承径向位移变化Fig.14 Changes of radial displacement of single-row two-point contact turntable bearing

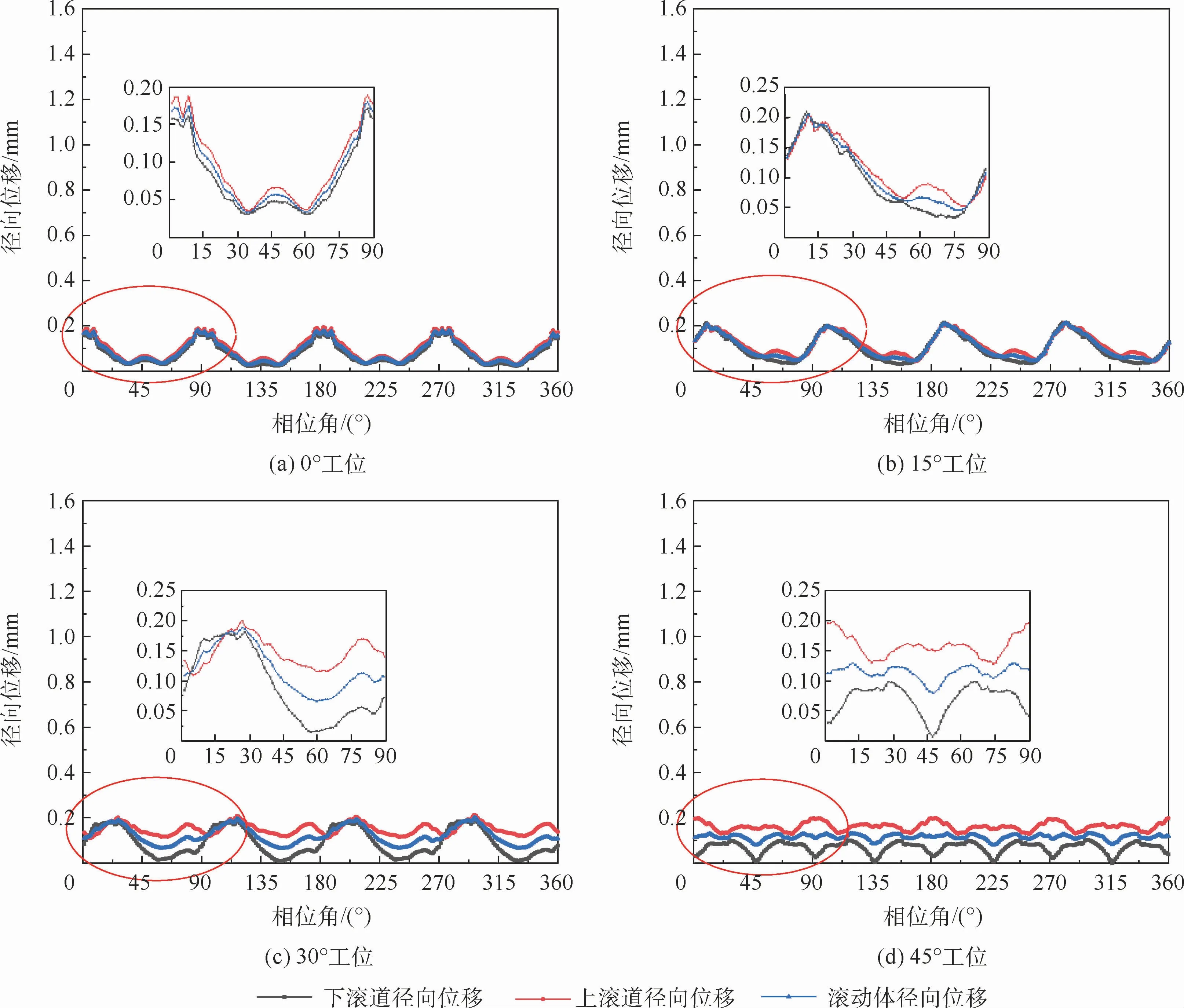
图15 单排4点接触式转盘轴承径向位移变化Fig.15 Changes of radial displacement of single-row four-point contact turntable bearing

图17 滚动体间隙简化计算Fig.17 Simplified calculation of rolling body clearance

图18 转盘轴承间隙变化对比Fig.18 Comparison of clearance changes of turntable bearing

仅考虑隔离块轴向滑落的情况，O是滚道横截面弧线对应的圆心，隔离块初始位置轴心与滚动体球心相重合记为O2，O2C为滚动体半径r1，当隔离块轴心下降至O′2时，隔离块外圆与滚道相切，此时O′2D为隔离块外圆半径r2。由三角函数和几何关系可得式（8）和式（10），可计算出隔离块下滑的距离O2O′2，记为Δh，如图19所示。

式中：R为滚道曲率半径，取值为78.5 mm；r1为滚动体半径，取值为40 mm；r2为隔离块外圆半径，取值为39.8 mm；∠O′2O2C为接触角，取值为30°。

计算可得隔离块下滑0.29 mm时，隔离块外圆与滚道相接触，接触点为D，由于隔离块锥面夹角为120°，滚动体间距增加值Δu与隔离块下滑距离Δh的关系如图20所示。

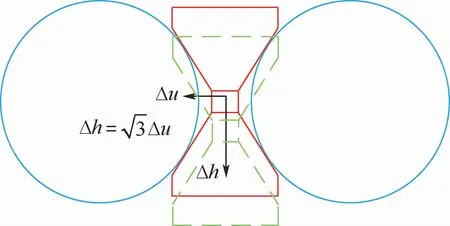
图20 滚动体与隔离块间距变化分析图Fig.20 Analysis of variation of distance between rolling body and isolation block

当滚动体间距增加0.167 mm时，隔离块与滚道相接触。在忽略转盘轴承安装间隙影响的基础上，加载后转盘轴承间隙增加值会导致8～35个隔离块滑落。

综上所述，转盘轴承在承载过程中滚动体之间间隙增加，下滚道发生轴向位移，使得滚动体在回转过程中不断“上坡”和“下坡”，并且滚动体驱动力具有时变性，导致滚动体运动状态不断变换，使得在连续回转过程中出现滚动体集聚和隔离块滑落的现象，影响转盘轴承的正常回转。

3 集聚效应对回转性能的实验

3.1 实验设计

为消除由滚动体间隙变化导致的集聚效应，并分析集聚效应对转盘轴承摩擦力矩的影响，在采用单排4点接触式滚道的基础上，设计了腹板式多孔结构分段保持架（简称腹板式保持架），其结构如图21所示。滚动体置于腹板式保持架的兜孔中，从机械结构的角度杜绝了滚动体集聚的可能性。

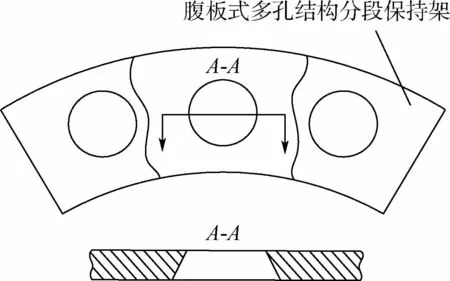
图21 腹板式多孔结构分段保持架Fig.21 Sectional retainer of web-type porous structure

发射台在轴向载荷条件下，以20°／min的速度回转。依据被测的转盘轴承不同，实验分为2组，分别记为I和II，如表1所示。通过数显液压表实时记录液压马达输入端和输出端压力变化，如图22所示，在回转一周后，导出数据做差处理，可得到液压马达压差变化的数据。

表1 回转实验分组Table 1 Rotary exper imental group

3.2 摩擦力矩计算

结合液压马达输出扭矩的计算方法［23］，联立实验台的传动关系可得发射台回转力矩：

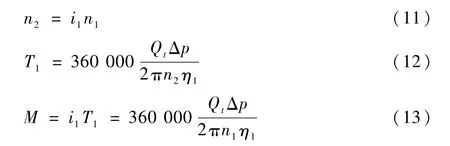
式中：i1为发射台传动比；Qt为实际流量，取值为20 L／min；η1为液压马达效率，取值为0.98；Δp为液压马达压力差；n1为转盘轴承的转速，取值为20°／min；n2为液压马达的转速；M 为发射台的回转扭矩。

发射台回转速度缓慢，其运动过程可以看作一个平稳过程，因此，摩擦力力矩与回转力矩大小相同：

3.3 实验结果分析

航天发射台在轴向负载条件下，匀速旋转，测得液压马达两侧压差如图23所示。

图23 液压马达压差变化曲线Fig.23 Hydraulic motor differential pressure curve

结合发射台传动关系，可绘制2组转盘轴承等效摩擦力矩的变化趋势，如图24所示。结果表明，II组实验中，在发射台开始回转后，滚动体之间间隙增加，隔离块出现滑落的现象，导致等效摩擦力矩不断变大并且稳定性较差。

对图24转盘轴承等效摩擦力力矩做统计分析，如图25所示，I组等效摩擦力矩的变化幅值为14 031.62 N·m，相对II组下降了47.82%，平均值下降了32.44%，在克服滚动体集聚效应后，转盘轴承回转稳定摩擦力矩显著下降。

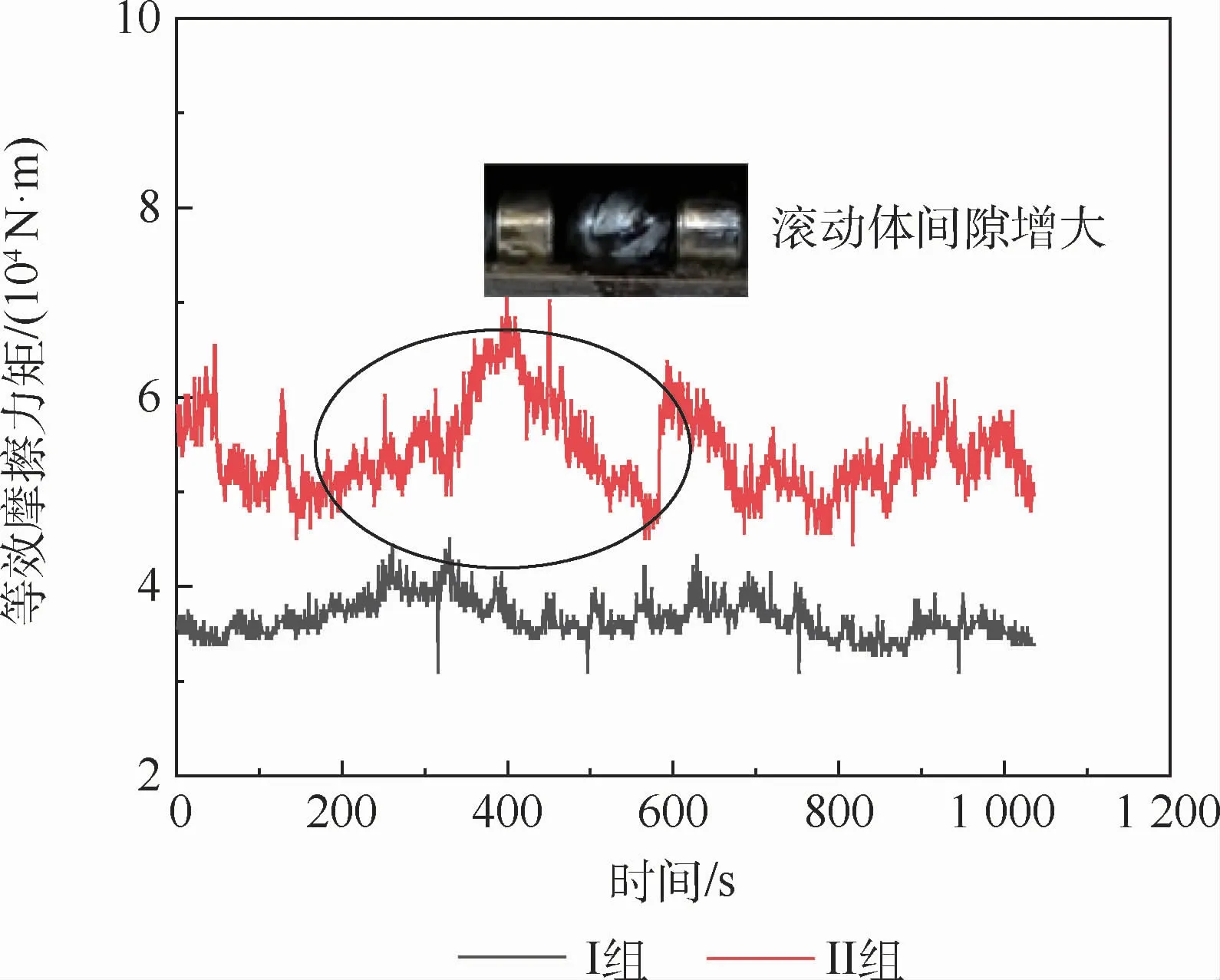
图24 转盘轴承等效摩擦力矩变化Fig.24 Variation of equivalent friction moment of turntable bearing

图25 等效摩擦力矩对比Fig.25 Comparison of equivalent friction moments

腹板式保持架有效降低了发射台回转时的摩擦力矩，且回转平稳性得到了提高。与隔离块的结构对比，腹板式保持架固定的兜孔使滚动体不因滚道位移或载荷变化而改变相邻滚动体间距，滚动体始终稳定运动，弥补了大型转盘轴承中隔离块与滚球接触不稳定的缺陷。

4 结 论

以航天发射台大型转盘轴承为研究对象，对比分析了动态载荷作用下，滚道结构对滚动体接触作用力、滚道变形和滚动体间隙的影响，阐明了转盘轴承发生集聚效应的原因，并提供了优化方案，通过实验的方式验证了方案的有效性，得出以下结论：

1）航天发射台转盘轴承在承载过程中滚道刚性变化具有时变性，不同滚道结构的轴向位移分布规律相同，发射台工位的变化仅对轴向位移的幅值有影响。由于下滚道轴向发生位移，滚动体不断交替进行“爬坡”和“下坡”。

2）单排2点接触式转盘轴承滚道径向刚度薄弱导致滚动体沿径向发生位移，滚动轴承间隙增加较多。滚动体接触作用力同样具有时变性，最大接触作用力始终在载荷的正下方区域，滚动体驱动力不断变化。因此，滚球变化的运动状态导致间隙集中，使得滚动体之间隔离块滑落，使转盘轴承产生集聚现象。

3）为避免转盘轴承出现集聚效应，采用径向刚度较好的单排4点接触式转盘轴承和腹板式保持架作为优化的新型轴承，并与使用隔离块的单排2点接触式转盘轴承进行摩擦力矩对比实验，结果表明，避免滚动体集聚可有效减小摩擦力矩，提高发射台回转稳定性。

4）采用静力学模型对发射台多个典型工位进行计算，无法实现发射台动态回转过程的实时分析，建立发射台动力学模型对于分析发射台回转过程中转盘轴承运动变化有着重要意义，需要进一步研究。