航天用6005A铝合金热变形行为研究

王胜龙 秦中环 周小京 刘建峰 张海超 董 阳 郭晓琳

航天用6005A铝合金热变形行为研究

王胜龙1秦中环1周小京1刘建峰2张海超2董 阳3郭晓琳1

(1. 北京航星机器制造有限公司，北京 100013；2. 山东大学，济南 250014；3. 山东兖矿轻合金有限公司，邹城 273515）

通过Gleeble-3800热模拟试验机对6005A铝合金在623～823K温度和0.01～10s-1应变速率下进行热压缩试验，研究了6005A铝合金热变形行为。基于试验真实应力应变数据，进行了温度修正和摩擦修正，建立了考虑应变补偿且能够准确描述6005A铝合金材料热变形过程中流变应力与应变、应变速率和变形温度之间关系的Arrhenius本构关系模型，相关系数为0.9985315，平均相对误差为2.56%。

6005A铝合金；热变形行为；真应力-应变曲线；本构方程

1 引言

6005A铝合金是一种中等强度的Al-Mg-Si系铝合金，具有密度低、挤压性好、焊接性好、力学性能好等优点，在民用型材挤压中得到广泛应用，尤其是在大型薄壁、空心型材等方面的应用[1，2]。近年来，随着我国航天武器装备事业的飞速发展，产品型号结构功能一体设计对6005A铝合金型材提出诸如截面复杂、内孔多、筋板多、壁厚差大、成形性优越、尺寸精度高、综合性能好等更高的要求，而要达到这些要求需要科学合理的模具结构设计和精确的热变形参数保证。因此，研究航天用6005A铝合金在一系列变形条件下的热变形行为，探究合金的本构关系模型、显微组织变化规律和加工性能对指导6005A铝合金热塑性加工具有十分重要的作用。

热变形中的材料流动行为十分复杂，受到材料动态软化和加工硬化的综合影响，建立温度同流变应力、应变之间的本构模型对于预测流动应力十分重要。目前一些学者对其它牌号的铝合金本构模型构建方面进行了大量的研究。Chen等[3]研究了6026铝合金在应变速率范围为0.001～10s-1和变形温度范围为673～823K条件下的流动应力行为，并且建立了考虑应变补偿的Arrhenius本构模型。Liu等[4]对6063铝合金在应变速率范围为0.01～10s‍-1和变形温度范围为573～723K条件下进行了热压缩试验，建立了考虑应变补偿的本构方程模拟热变形行为。

虽然目前对铝合金热变形行为的研究已有一定的基础，但是不同热变形参数下航天用6005A铝合金的流变行为却鲜有报道。本研究通过Gleeble-3800热模拟试验机进行等温、等应变速率的热压缩试验，分析材料的流变应力行为，对真应力-应变曲线进行温度和摩擦修正，建立6005A铝合金材料考虑应变补偿的本构模型。

2 热压缩试验

热压缩试验在热模拟试验机（Gleeble-3800）上开展，本研究所用材料为均匀化处理后的铸态航天用6005A铝合金，在均匀化处理后的铸锭1/2半径处，通过线切割获取直径为10mm、高度为15mm的圆柱形光滑试样。变形温度分别为设置为623K、673K、723K、773K、823K，应热变速率分别为0.001s-1、0.01s-1、0.1s-1、1s-1、10s-1，试验总压下量为60%，应变量为0.916。在试样两端面涂抹润滑膏并贴上石墨片以减小试样与压头之间的摩擦。样品采用热模拟机电阻加热，以10K/s的升温速率加热至热压缩温度后保温3min，然后进行恒定应变速率的热压缩试验。压缩完毕后，立刻取下试样并对试样喷水处理，保留金属变形组织。压缩过程中由Gleeble-3800热模拟机的计算机系统自动采集真应力、真应变、实时温度、实时压缩高度、实时应变量等数据。

3 结果与讨论

3.1 真应力-应变曲线分析

3.1.1 真应力-应变曲线

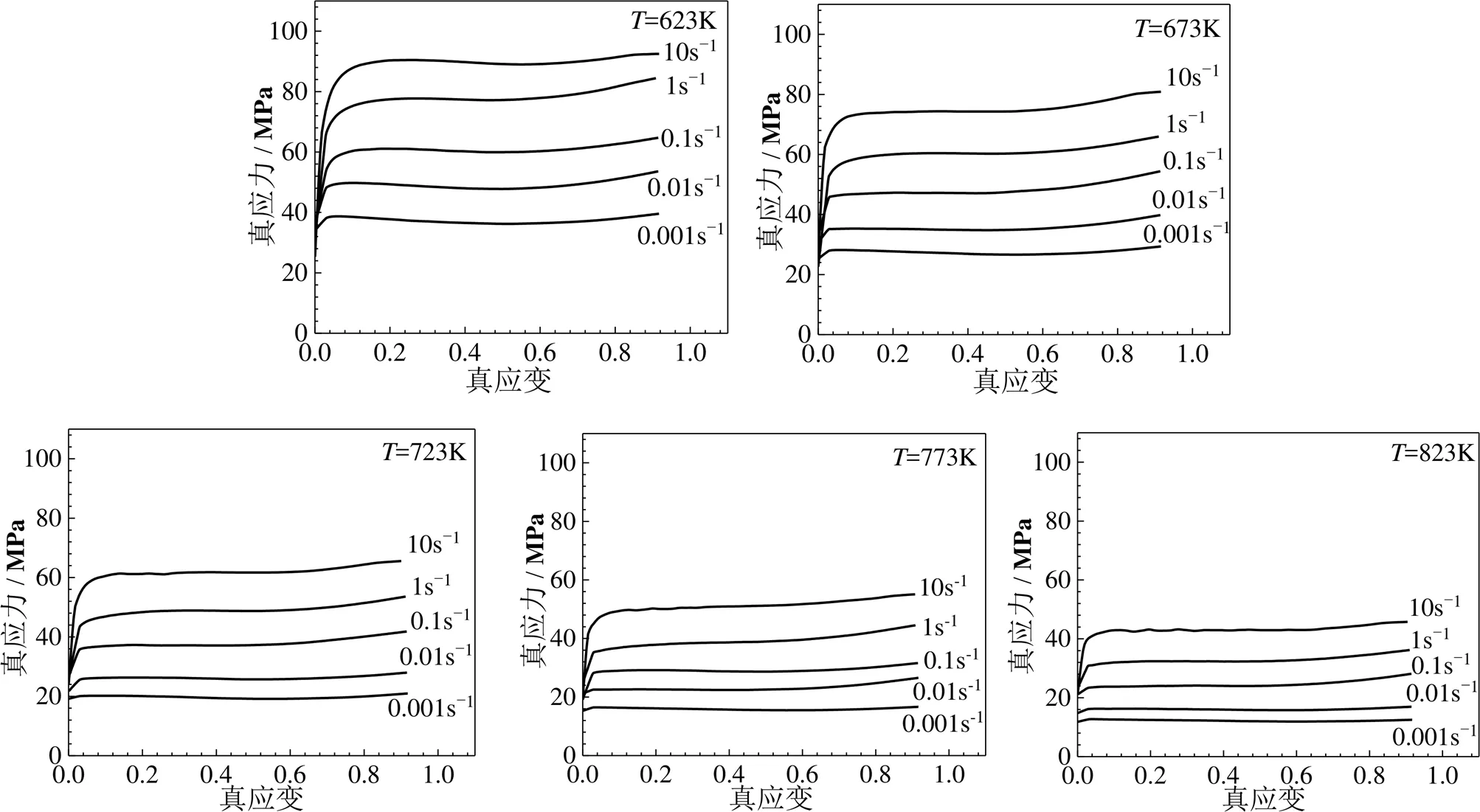
图1 6005A铝合金在不同变形条件下实测真应力-应变曲线

图1为通过热压缩试验数据计算得到的不同应变速率和不同试验温度下的真应力-真应变曲线。图1显示，在相同的应变速率和变形温度下，真应力随着真应变的增加先迅速增加，达到峰值之后略有下降或趋于稳定，而后平缓变化，在变形最后阶段有所增加。这是在塑性变形过程中动态软化和加工硬化相互作用的结果，动态回复和动态再结晶产生动态软化，位错增殖以及位错间的相互作用产生加工硬化。当加工硬化作用大于动态软化作用时，流变应力呈上升趋势；当动态软化作用大于加工硬化作用时，流变应力呈下降趋势；二者相当时，流变应力趋于稳定而平缓变化[5，6]。在低应变量阶段，位错迅速增加，位错之间的相互作用强，加工硬化作用明显，此时无足够强的能量驱动动态软化发生，从而流变应力急剧上升。应变量增加到一定程度后，晶体内能量增加，驱动动态软化发生，且软化作用逐渐增强，加工硬化被抵消，直到二者作用趋于平衡，流变应力在这个过程中趋于稳定而平缓变化。随着变形程度增加，热模拟试验机压头与圆柱形试样端面接触面积逐渐增大，摩擦力增大，金属变形难度提高，导致流变应力略有上升[7]。

由图1还可看出，在同一变形温度下，流变应力会随着应变速率的增加而显著增加，故6005A铝合金是应变速率敏感材料。随着应变速率增加，高密度位错形成速度加快，加工硬化作用明显增强，同时动态软化时间变短，软化不充分，因此流变应力明显提高[8]。在同一应变速率下，随着变形温度升高，流变应力显著降低，主要是由于热激活能增强[3]，位错等缺陷活动能力提高，晶界迁移变化容易，动态回复和动态再结晶作用增强而导致的。

3.1.2 真应力-应变曲线的温度和摩擦修正

在热压缩过程中，变形产热和摩擦产热会造成试样温度升高，但受热压缩机温控装置灵敏度限制，温控装置无法及时调整温度变化，导致流变应力曲线反映的温度有所偏离设定的温度。此外，热压缩过程中试样两个端面与热压缩机压头之间仍存在一定的摩擦，导致试样腰部出现“鼓肚”现象，难以做到理论上轴向和横向应变相等的无“鼓肚”均匀变形。由于温度和摩擦所带来的误差导致试验结果不能精确反映试样变形的真实情况，需要对试验采集到的应力应变数据进行修正。

3.1.2.1 真应力-应变曲线的温度修正

采用式（1）[9]修正温度对流变应力的影响。

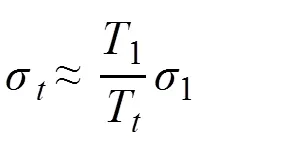
式中：T1为热压缩试验的实测温度；Tt为热压缩试验设定的温度；σ1为热压缩试验的实测应力；σt为温度修正后的应力。

在不同变形条件下实测真应力-应变曲线与温度修正后真应力-应变曲线的比较如图2所示。由图2可看出，流变应力达到峰值应力之前的低应变下，温度修正作用较小，修正效果随着应变的增加而逐渐变好。随着应变速率增加，修正后的应力值越大于实测值，随着应变速率越低，修正后的应力值越接近实测值。在高应变速率下材料变形剧烈，变形时间短，受热压缩机温控设备灵敏度限制，对变形热或者摩擦热导致的温差调控不够及时，与设定温度相比会出现一定的偏差。在低应变速率下，变形时间长，热压缩机温控设备可以及时反应来调控由变形热或者摩擦热导致的温差[10]。高应变速率下，材料变形剧烈导致单位时间内的产热多，温升大，大的温升使材料软化，提高了材料的塑性，降低了材料的流变抗力。温度越低，温度修正效果越明显，由于同样应变速率下，单位时间内温升相似，温升与设定温度的比值越大，修正效果越明显。

3.1.2.2 真应力-应变曲线的摩擦修正

采用Ebranhimi 和Najafizadeh提出的式（2）[11]修正摩擦因素对流变应力的影响：

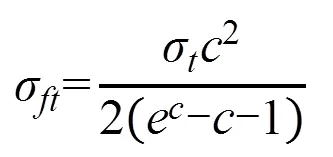
式中：σ为摩擦修正后的应力；σ为温度修正后的应力；为摩擦修正率。

式中：为试样的瞬时高度；为试样的瞬时平均半径；为摩擦接触因子。

式中：0为试样的初始高度；0为初始半径。利用试验结束后的试样形状尺寸计算摩擦接触因子：

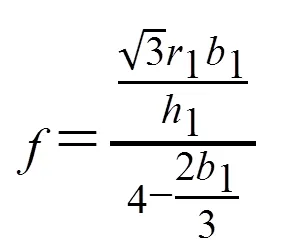
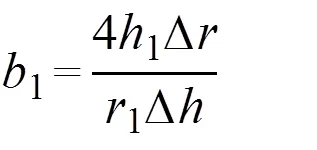
式中：1为试样变形后的高度；Δ为试样变形前后的高度变化值；1为试样变形后的平均半径；Δ为试样变形后的最大鼓肚半径r与试样变形后的端面（和压头接触位置）半径r之差。

试样压缩前后变化如图3所示。在不同变形条件下温度和摩擦修正后真应力-应变曲线与实测真应力-应变曲线的比较如图4所示。

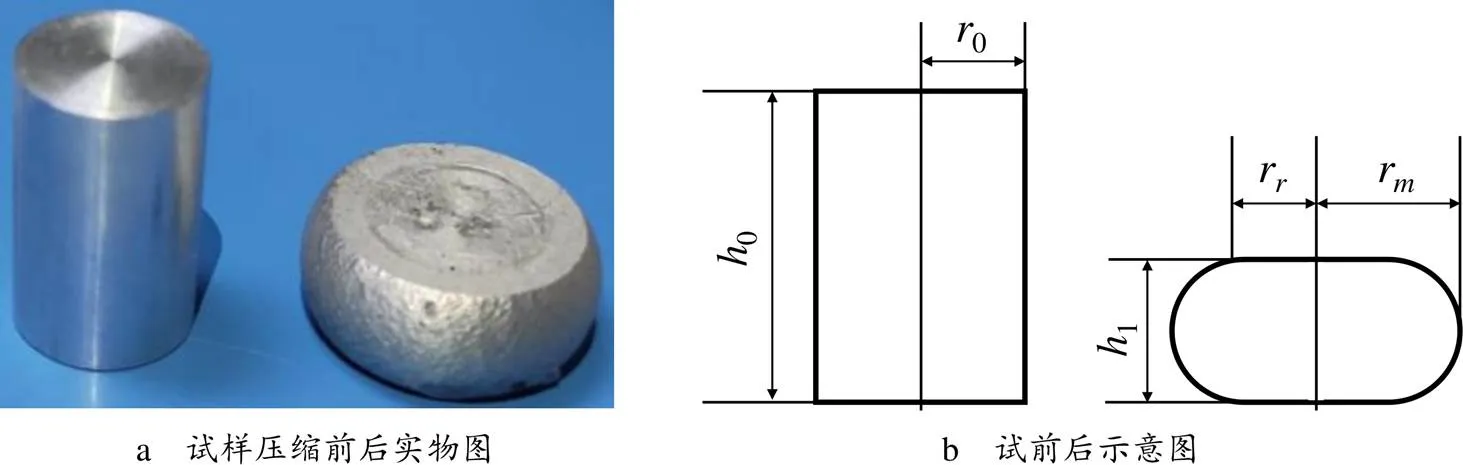
图3 热压缩变形试样

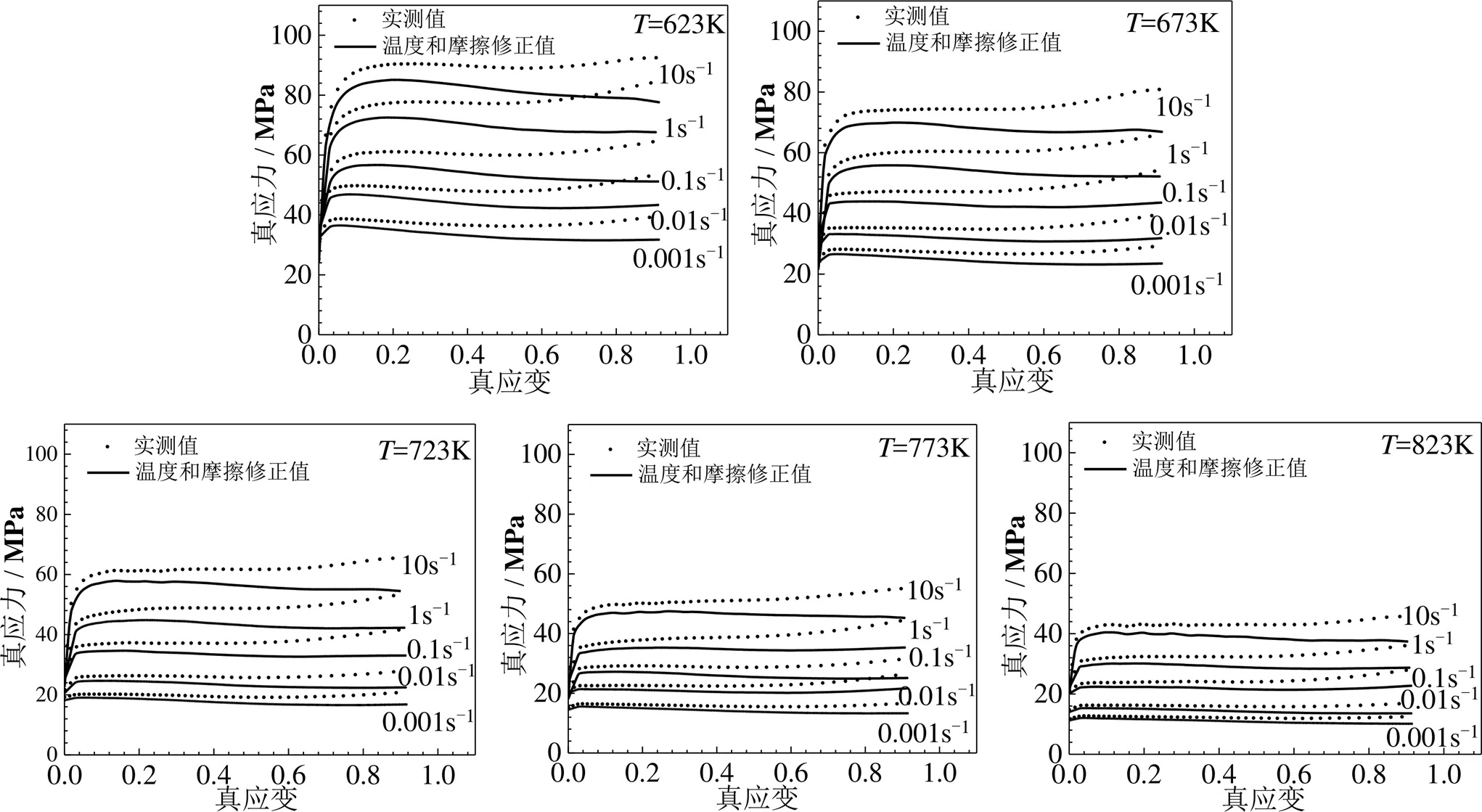
图4 6005A铝合金在不同变形条件下温度和摩擦修正后真应力-应变曲线与实测值曲线的比较

由图4可见，流变应力经摩擦修正后均小于实测值。在同一温度和应变速率下，摩擦对流变应力的影响作用随着应变量的增加逐渐增大，主要是因为随着压缩程度的增加，热模拟试验机压头与圆柱形试样端面接触面积明显增大，摩擦力增加而导致的结果。

3.2 考虑应变补偿的Arrhenius模型

根据经温度和摩擦修正后的真应力-真应变数据，采用考虑应变补偿的Arrhenius本构模型描述6005A铝合金的应力与应变速率、温度、应变之间的关系。Arrhenius模型的本构方程形式如式（7）所示。

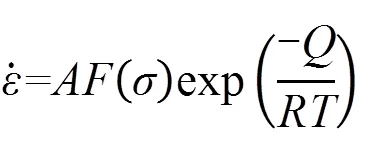
式中：1是试验中需要测得的材料常数，其中=1。

将式（8）带入式（7）中，Arrhenius模型的本构方程可以表示为：

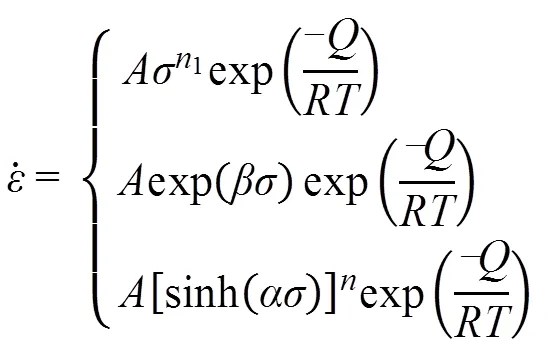
对两边分别取自然对数，可得：

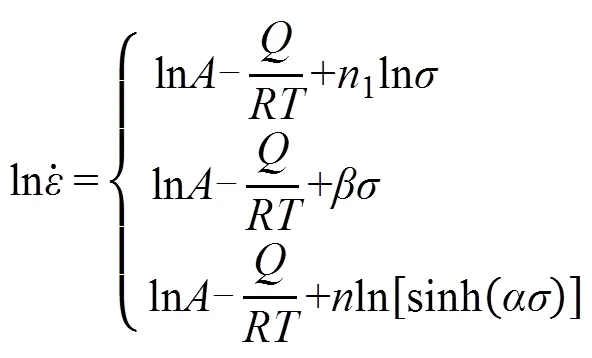
为了方便求解，做进一步转化，可得：

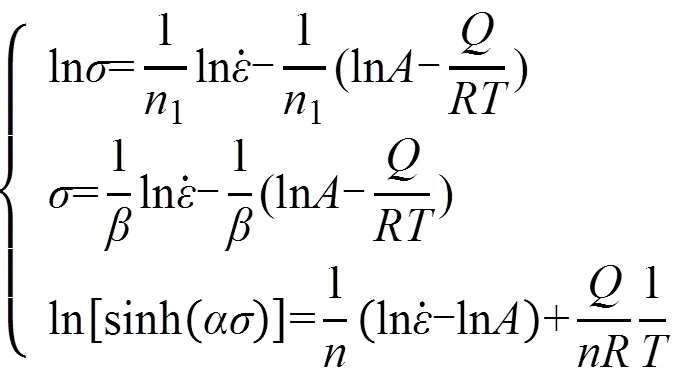
根据上面的方程可知，在温度一定时，、、关系曲线呈线性关系，如图5a、图5b、图5c所示。n1、β、n可通过、、关系曲线斜率平均值的倒数求得，Q和A可通过ln[sinh(ασ)]-1/T关系曲线斜率的平均值和截距的平均值求得。

取应变=0.6，与其对应的应变速率进行线性拟合，如图5所示。求1=8.0602268、=0.240916、=1=0.0298890、=5.954153、=164.648627kJ·mol-1、=6.6146847×1010s-1。

温度与应变速率的关系可用指数型zener-hollomon参数（一般称作参数）表示[12]。式（9）的本构方程可用参数表示如下：

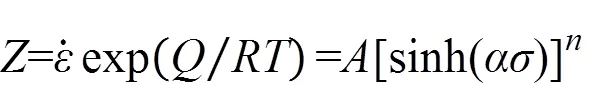
根据双曲函数定义，通过式（12），可将流变应力写成含参数的如下函数关系式：

将=0.6时求得的、和带入式（13），6005A铝合金流变应力可以表示为：

由以上公式推导可看出，式（14）中的流变应力只受到变形温度和应变速率的影响。然而材料参数、和的值受到应变的影响，将式（13）中的各项材料参数、和构建为含应变的多项式函数，然后分别取应变为0.05～0.85时的应力值（每隔0.05取一个应变对应的应力值），计算得到对应应变下的各项参数值。为了提高计算的精度，减少误差，本文使用六次多项式对各个材料参数进行拟合，如式（15）所示，得到的拟合曲线如图6所示，得到各个多项式函数的系数如表2所示。

图6 材料常数与应变的关系曲线

表2 6005铝合金材料常数α、Q、n和lnA多项式拟合的系数

将各个材料参数的多项式带入式（13）中，得到考虑应变补偿的本构方程，如式（16）所示。

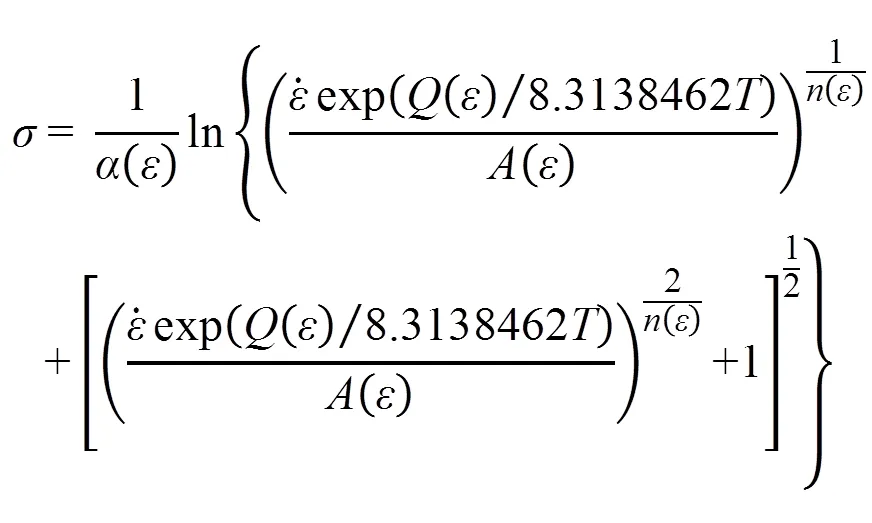
式中：()为关于应变的多项式函数；()为关于应变的多项式函数；()为关于应变的多项式函数；()为关于应变的多项式函数。

为了验证考虑应变补偿的本构方程对流变应力预测的准确性，将通过本构方程计算的预测值与温度和摩擦修正后的修正值比较，如7所示。

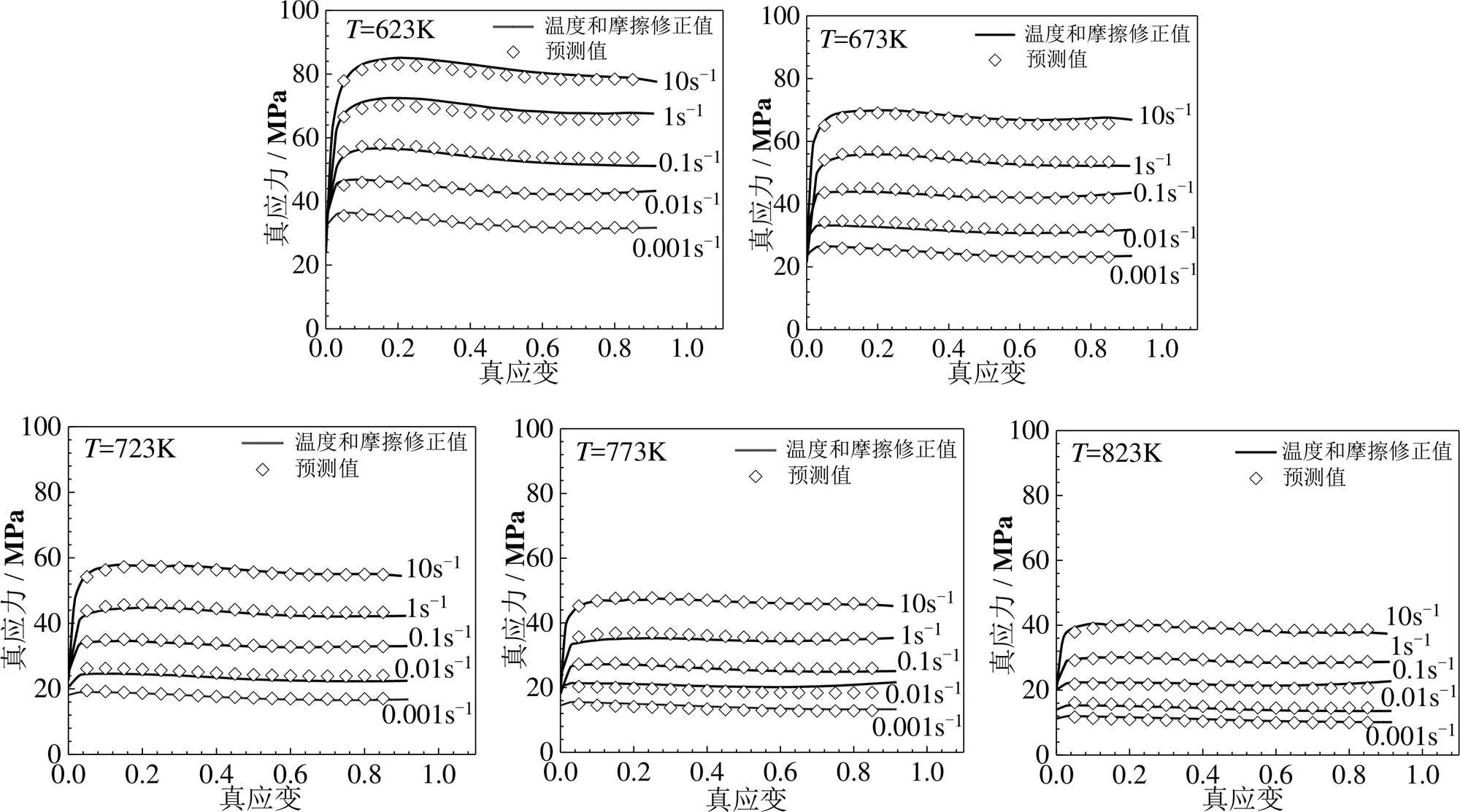
图7 6005A铝合金在不同变形条件下的试验修正流变应力与预测流变应力比较

由图7可看出，通过本构方程计算的预测结果与温度和摩擦修正后的结果拟合良好。为了对考虑应变补偿的本构模型预测结果进行量化，利用相关系数和平均相对误差对拟合情况进行评估。

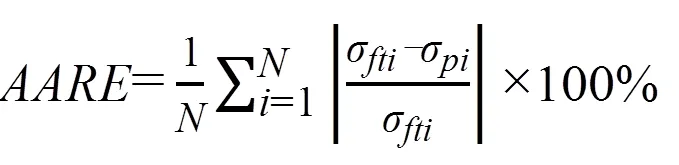
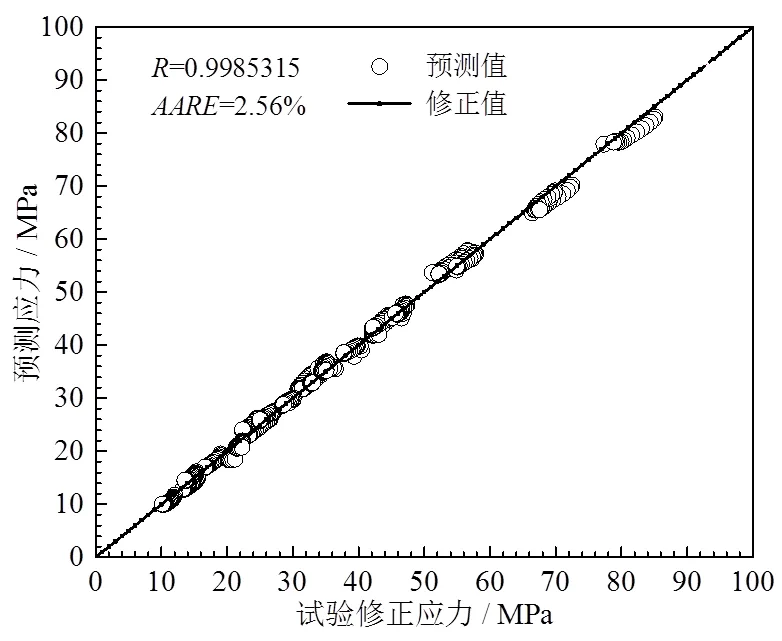
图8 预测应力值与试验修正应力值相关性对比

在应变为0.05～0.85的范围内，6005A铝合金预测应力值与试验修正应力值相关性对比如图8所示，经过计算，=0.9985315，=2.56%。因此，本文中考虑应变补偿的本构模型能够准确地描述6005A铝合金热变形过程中流变应力与变形温度、应变速率、应变之间的关系。

4 结束语

a. 6005A铝合金的流变应力行为与热变形条件有关。由于加工硬化和动态软化的相互作用，真应力在相同的应变速率和变形温度下，随着真应变的增加先迅速增加，达到峰值之后，略有下降或者趋于稳定，而后平缓变化，在变形最后阶段有所增加。在同一变形温度下，流变应力会随着应变速率的增加而显著增加，说明了6005A铝合金是应变速率敏感材料。

b. 基于应力应变数据建立的考虑应变补偿的Arrhenius本构模型为：

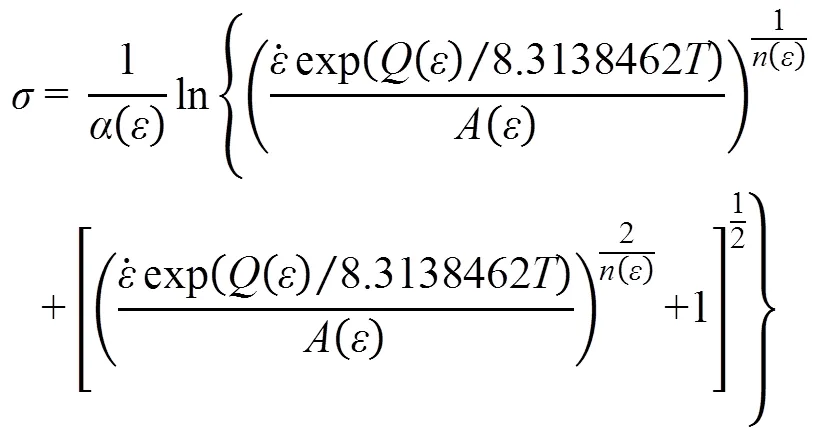
可以准确地描述6005A铝合金热变形过程中流变应力与变形温度、应变速率、应变之间的关系，相关系数为0.9985315，平均相对误差为2.56%。

1 杨丽，吴海旭，秦利，等. 地铁车体用 6005A-T6 铝合金型材的理化检验[J]. 轻合金加工技术，2014，42(9)：44～47

2 周小京，郭晓琳，东栋，等. 6005A铝合金挤压型材在线淬火工艺仿真研究[J]. 航天制造技术，2019(3)：7～13

3 Chen Liang, Zhao Guoqun, Yu Junquan. Hot deformation behavior and constitutive modeling of homogenized 6026 aluminum alloy[J]. Materials and Design, 2015, 74: 25～35

4 Wu Ronghai, Liu Yang, Geng Cong, et al. Study on hot deformation behavior and intrinsic workability of 6063 aluminum alloys using 3D processing map[J]. Journal of Alloys and Compounds, 2017, 713: 212～221

5 Deng Ying, Yin Zhimin, Huang Jiwu. Hot deformation behavior and microstructural evolution of homogenized 7050 aluminum alloy during compression at elevated temperature[J]. Materials Science & Engineering A, 2011, 528(3): 1780～1786

6 Jin Nengping, Zhang Hui, Han Yi, et al. Hot deformation behavior of 7150 aluminum alloy during compression at elevated temperature[J]. Materials Characterization, 2008, 60(6): 530～536

7 仇琍丽，高文理，陆政，等. 7A85铝合金的热压缩流变行为与显微组织[J]. 材料工程，2016，44(1)：33～39

8 刘文义. 7085 铝合金热加工力学行为及微观组织演变规律研究[D]. 重庆：重庆大学，2014

9 杨昭. 铝合金轴箱体锻造工艺设计与金属变形规律研究[D]. 山东：山东大学，2018：14～15

10 Li Luoxing, Zhou Jia, Duszczyk J. Determination of a constitutive relationship for AZ31B magnesium alloy and validation through comparison between simulated and real extrusion[J]. Journal of Materials Processing Tech., 2005, 172(3): 372～380

11 Ebrahimi R, Najafizadeh A. A new method for evaluation of friction in bulk metal forming[J]. Journal of Materials Processing Tech., 2004, 152(2): 136～143

12 Zener C, Hollomon J H, Effect of strain rate upon plastic flow of steel[J], Appl. Phys. 1944, 15: 22～32

Research on Thermal Deformation Behavior of 6005A Aluminum Alloy Used in Aerospace

Wang Shenglong1Qin Zhonghuan1Zhou Xiaojing1Liu Jianfeng2Zhang Haichao2Dong Yang3Guo Xiaolin1

(1. Beijing Hangxing Machinery Manufacture Co., Ltd., Beijing 100013;2. Shandong University, Jinan 250014; 3. Shandong Yancon Light Alloy Co., Ltd., Zoucheng 273515)

The thermal compression test of 6005A aluminum alloy at 623～823K and 0.01～10s-1was carried out by Gleeble-3800 thermal simulation testing machine, and the thermal deformation behavior of 6005A aluminum alloy was studied. Based on the true stress and strain data of the experiment, temperature correction and friction correction were carried out, and the Arrhenius constitutive model of 6005A aluminum alloy considering strain compensation was established, which can accurately describe the relationship between flow stress and strain, strain rate and deformation temperature duringthermal deformation of 6005A aluminum alloy. The correlation coefficientis 0.9985315, and the average relative erroris 2.56%.

6005A aluminum alloy；thermal deformation behavior；true stress-strain curve；constitutive equation

TG146.2

A

国防基础科研计划资助项目（JCKY2018204B034）。

王胜龙（1988），博士，材料科学与工程专业；研究方向：轻合金热加工成形技术。

2021-09-06