狭义相对论教学中的几个问题

王 雷

(东南大学 物理学院，江苏 南京 211189)

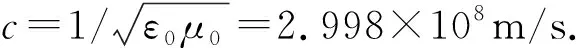
1 常见例子的问题

在否定经典理论时,经常有投球时序颠倒和超新星爆发过程中光线传播的例子,下面以超新星爆发为例进行说明, 如图1所示.物质向各方飞散,假设光相对光源的速度为c,则A点光线到达地球所需时间tA=l/(c+v).B点光线到达地球所需时间tB=l/c.理论计算超新星爆发的强光的时间持续约为Δt=tB-tA≈25年,实际持续时间约为 22个月.而根据当时的基本理论,光在以太系速度为c,则在地球静止系光速应与光源速度无关,所以上述实验假设光相对光源的速度为c是错误的,不能否定掉当时的理论.

图1 超新星爆发示意图

2 洛伦兹变换

设有1和2两个事件在S和S′系的时空坐标分别为

上述的差分形式有很多优点.一般两个参考系通常不满足在t=0时重合,而差分形式是适用的,可引入与S系相对静止的S″系,S″系与S′系满足t′=t″=0时重合,再利用Δx″=Δx,Δt″=Δt,得到上述变换.也可方便的相除得到速度变换.定义清楚两个事件,在两个参考系分别写坐标差与时间差,代入关系即可得正确结论.

3 同时的相对性

如图2所示，设地面为S系，S′系固定于以速度v运动的车厢,事件 1 ：车厢后壁接收器接收到光信号.事件 2 ：车厢前壁接收器接收到光信号.在S′系同时到达前后壁，而在S系因为车的前进,光先到后壁,再到前壁,即同时是相对的.

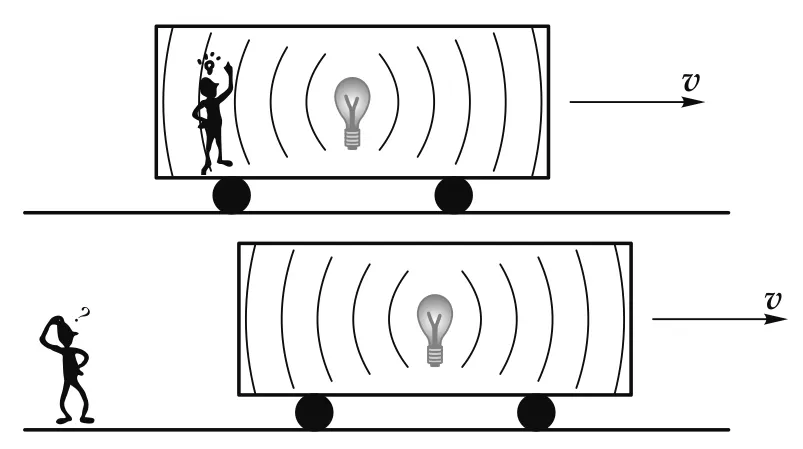
图2 同时相对性

在S′系中，如图3所示，光到达后前壁1、2处表的读数相同；光到达前壁时前壁表的读数t′2为同时同地，则在S系亦应如此，后壁类似，下面给出在S系看到的现象. 设S系观察者与光源在同一位置时为此处两参考系数0时,光源同时发光.下面求出此时1、2处表的读数，有

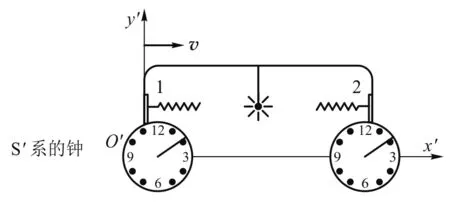
图3 同时同地的绝对性

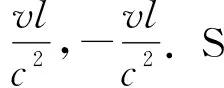
4 长度收缩

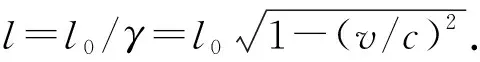
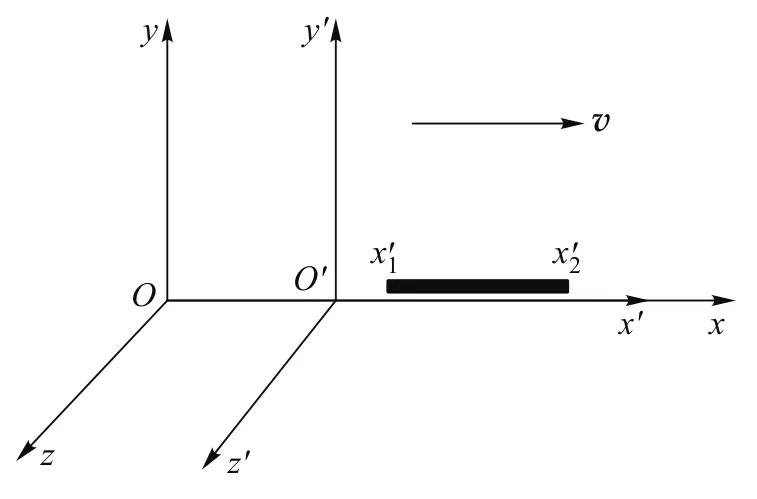
图4 长度收缩

下面讨论一下从S′系看S系的测量过程.设S系中的人拿一尺子,同时记录某时刻木棒两端坐标,则在S′系看来有

可见不同参考系现象不同, 但是所有结论满足洛伦兹变换.

长度收缩公式也适用于两相对静止点距离在不同参考系的关系,现考察下面例子:静系中μ子的平均寿命为τ0=2.2×10-6s. 在一组高能物理实验中，μ子以速度v=0.996 6c竖直向下朝地球运动，通过的平均距离为8 km. 按经典力学时空观，通过的平均距离为660 m，试说明这一现象.

在S′系(μ子静止系)中地球相对μ子飞L0=vτ0,也为μ子相对地球的飞行距离660 m.在S系(地球静止系)Δx=γ(Δx′+vΔt′)=γL0,其中因为μ子在S′系静止,Δx′=0.可见对两个相对运动的物体,用长度收缩公式是不适合的，需要直接用洛伦兹变换.

5 时间的延缓

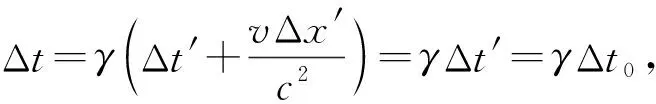
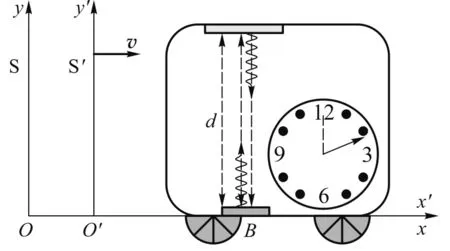
图5 时间延缓

考虑下面的问题, 如图6所示，在S系中的x轴上距离为l处有两个同步的钟A和B，在S′系中的x′轴上有一个同样的钟A′.设S′系相对于S系沿x方向以速度v运动，且当A′与A相遇时，两钟的读数均为0. 那么如图7所示，当A′钟与B钟相遇时，在S系中B钟的读数是tB=l/v；此时在S′系中A′钟的读数是t′A=l/(γv).B钟的读数较大，在S系中因为A′走的慢，读数小，合理. 由同时同地的绝对性，在S′系亦如此，而在S′系A、B运动，则B走的慢，为什么读数大呢？

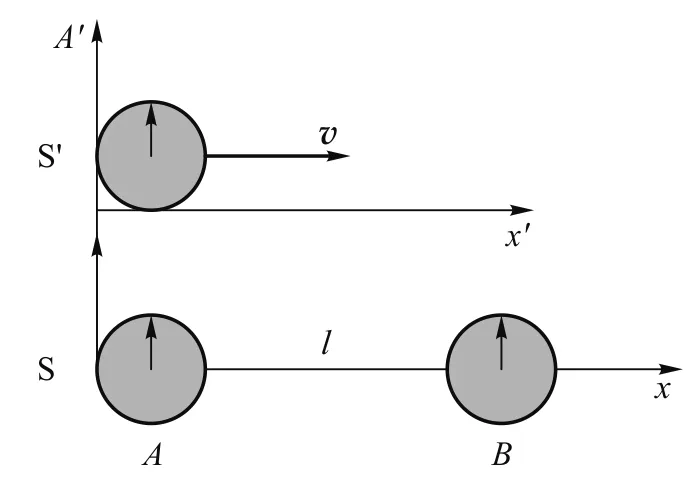
图6 运动系不同地的时间1

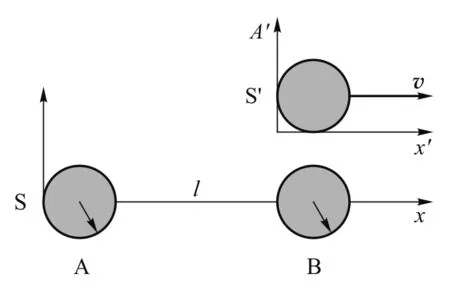
图7 运动系不同地的时间2

由此可知相对运动的参考系内,各点时间各不相同,尽量在静止系内写变量差分,由洛伦兹变换得到在运动系的形式,也可通过以上的例子练习后掌握写运动系正确结论的方法.

6 光的多普勒效应的推导

如图8所示，设t=0时,波源(S系O点)和观察者(S′系O′点)在S系距离为x0,S′系相对S系的速度为v,沿x轴正向.波源每隔周期T发一相同信号,考虑观察者接收0、T信号的时间差：

注意到S′系接收信号为同一地点,时间差为固有时：

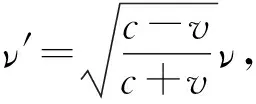
图8 光的多普勒效应